考慮伺服系統增益不確定的船舶動力定位自適應有限時間控制
張國慶 黃晨峰 吳曉雪 張顯庫
由于海洋資源開發和海洋工程作業的需要,人們對于深海作業的浮式生產系統(半潛平臺、生產油船、供給船等)的定位方式日益重視.船舶動力定位技術是指在不借助錨泊系統的情況下,船舶利用自身的推進裝置抵御風、浪、流等外界擾動的影響,以一定的姿態保持在海面某一目標位置或精確地跟蹤某一軌跡,以完成各種作業的功能[1?3].它具有不受海水深度影響、定位準確快速等優點.由于水面船舶不可避免地將遭受如風、浪和流等外部環境帶來的強擾動,以及復雜的水動力的不確定性,給控制器的設計帶來巨大的困難[4?6].同時,船舶的縱蕩,橫蕩和艏搖三個自由度之間存在著強耦合,且其中任一自由度的不穩定都將對整個系統造成巨大影響,所以要求三個自由度同時穩定[7].Do[8]基于李雅普諾夫直接法提出了一種輸出反饋的控制方法,通過構造自適應觀測器來估計船舶的速度和未知參數,設計的控制器能夠迫使船舶位置和艏向角漸近穩定于期望值.Du等[9]采用高增益觀測器對船舶的位置和艏向角進行估計,并引入徑向基函數(Radial basis function,RBF)神經網絡補償船舶模型的不確定性,設計的控制器不需要模型和外界擾動的先驗知識.王元慧等[10]基于非線性模型預測控制技術設計了船舶動力定位控制器,并通過仿真驗證了非線性模型預測控制器的有效性.Hassani等[11]提出了一種基于多模型的濾波理論的反饋控制方法,通過對時變海洋環境中的高頻部分進行濾波,使船舶在惡劣海況下的動力定位性能得到顯著提高.Grovlen等[12]通過引進矢量逆推的概念,在控制器設計過程中忽略了時變環境擾動的影響,從而簡化了船舶動力定位控制律逆推方法,并且得到全局指數穩定的結果.以上研究大多得到的是漸近穩定或指數穩定的控制結果,鮮有基于有限時間理論[13]的船舶動力定位控制方法的相關文獻.為此,在考慮伺服系統增益不確定的前提下,針對模型參數不確定、外部擾動未知的船舶動力定位控制問題,本文提出了一類自適應非奇異終端滑模的控制方法,并通過Lyapunov穩定性理論證明了閉環系統是實際有限時間穩定的,最后采用一艘供給船進行數值仿真實驗,證明了所設計控制器的有效性.本文的創新點主要有:1)設計了一種終端滑模的控制方法,實現了船舶動力定位系統運動學回路和動力學回路的雙環有限時間穩定,且收斂精度高,魯棒性強;2)針對伺服系統的增益不確定問題引入自適應參數學習律,避免了再在執行部分構建控制命令–執行變量之間的閉環,得到了控制輸入為實際可測螺距變量的結果,更易于工程實現.
1 問題描述與預備知識
1.1 預備知識
為了方便后續分析,這里給出有限時間穩定的相關定義和引理[14?17].考慮如下非線性系統:
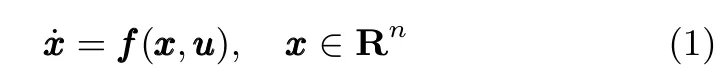
其中,x為狀態變量,入變量,為連續函數,且f(0)=0.如果系統(1)是Lyapunov穩定的,且存在時間函數,使得對于所有的t≥恒成立,則稱系統(1)是有限時間穩定的[14].
引理1.針對式(1)描述的系統,假設存在連續可微的正定函數,標量λ>0,0<α<1和0<ζ<∞,使得式成立,則可以說系統 x˙ =是PFS的[5].且到達時間為
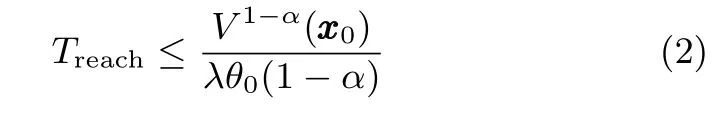
引理2.對于任意實數xi,如果存在r∈(0,1),則有下述不等式成立[16]:
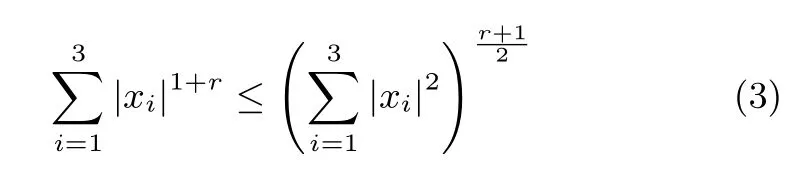
引理3.對于任意實數xi,如果存在r∈(0,1),則有下述不等式成立[17]:
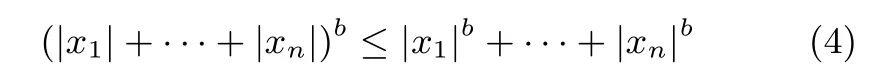
1.2 動力定位船舶的數學模型
假設動力定位船舶是左右對稱的,只考慮船舶前進、橫漂和艏搖3個自由度的平面運動,則動力定位船舶的非線性模型為
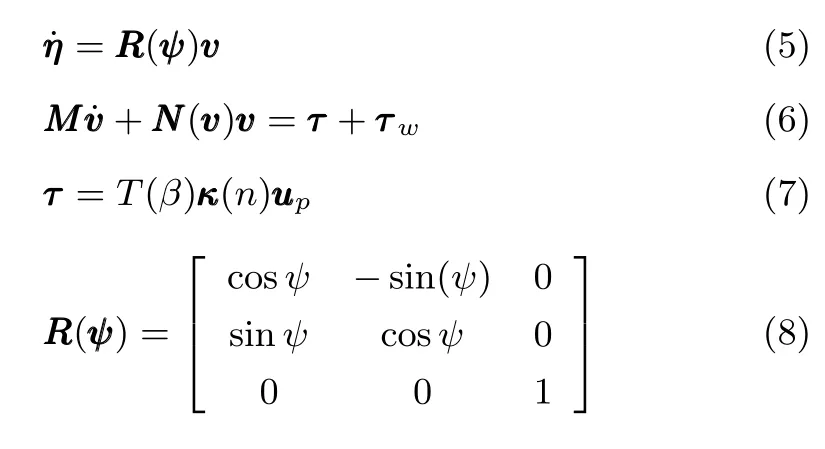
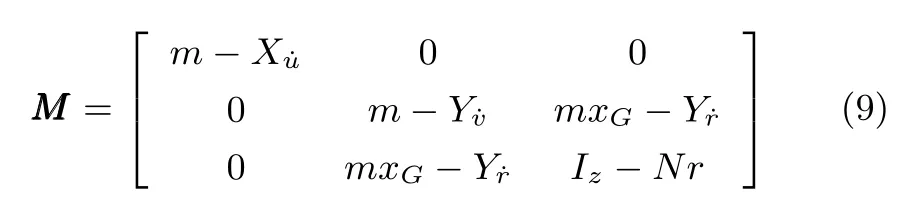
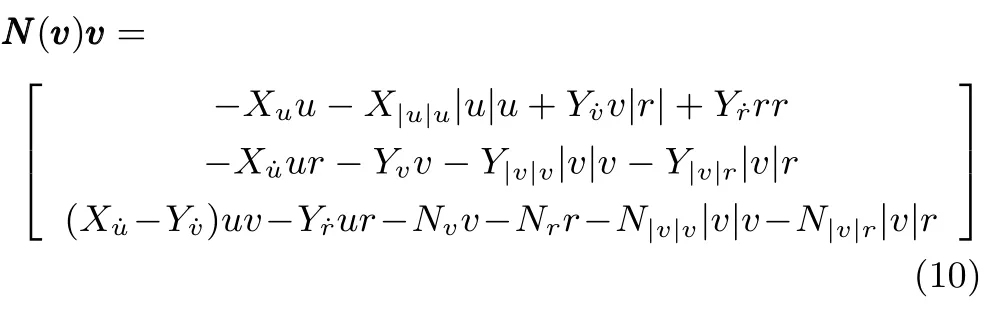
假設1.慣性矩陣為M是正定可逆的對稱矩陣,即M.該假設與水面船舶船體左右,前后近似對稱的特性是相符的.
假設2.M和 N(v)為未知模型參數矩陣且上界已知,其滿足下列條件:
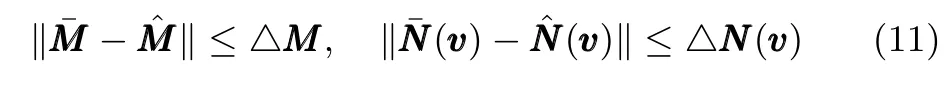
假設3.在式(6)中,τw為上界已知的擾動,即存在向量且.
注1.考慮實際海洋工程中主機提供給推進器的能量是有限的,因此,對于特定的船舶來說,推力系數矩陣必須滿足為未知常量且僅用于穩定性分析.
2 非奇異終端滑模控制器設計
將船舶動力定位系統的控制器設計分為兩步.首采用Lyapunov直接法設計運動學回路的有限時間虛擬控制律;然后基于非奇異終端滑模的方法設計系統的動力學回路控制器,同時考慮船舶動力定位系統執行器的增益不確定問題,最終設計出符合海洋工程實踐,控制輸入為調距槳可變螺距的船舶動力定位自適應有限時間控制律.
步驟1.船舶動力定位的期望軌跡為,定義船舶動力定位的位置誤差為

對時間求導,可得

將v視為虛擬控制向量,選擇鎮定函數向量αv為
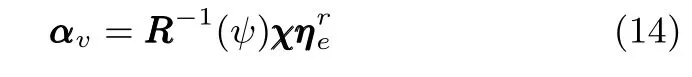
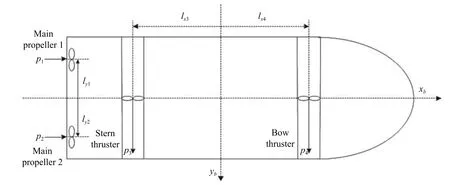
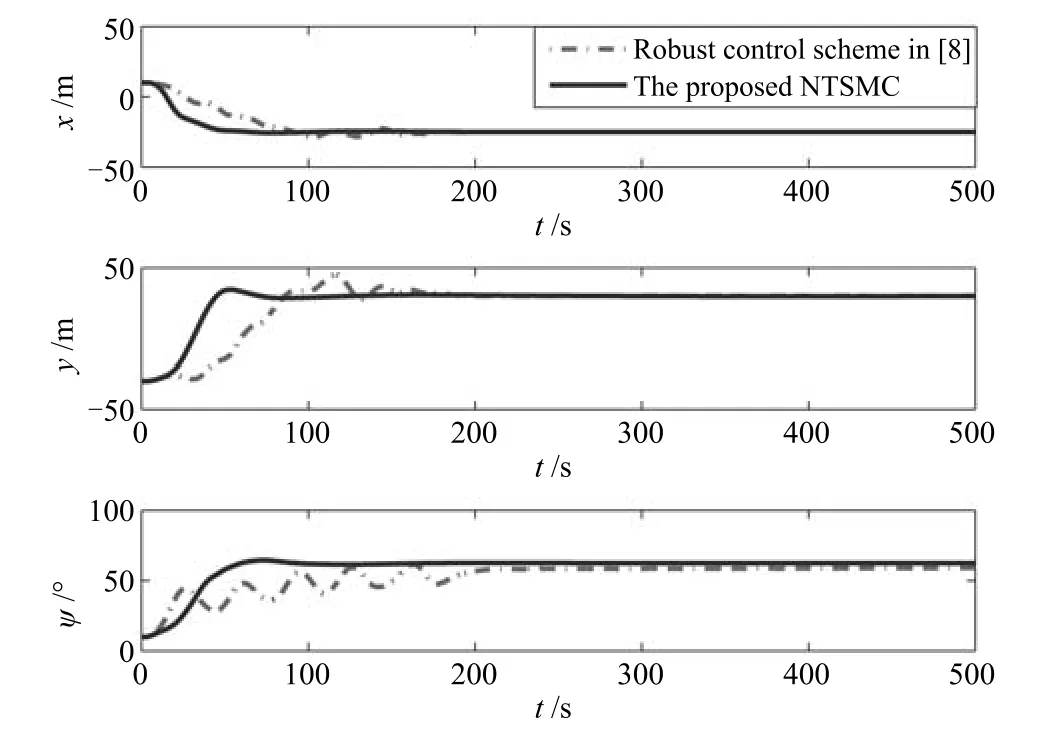
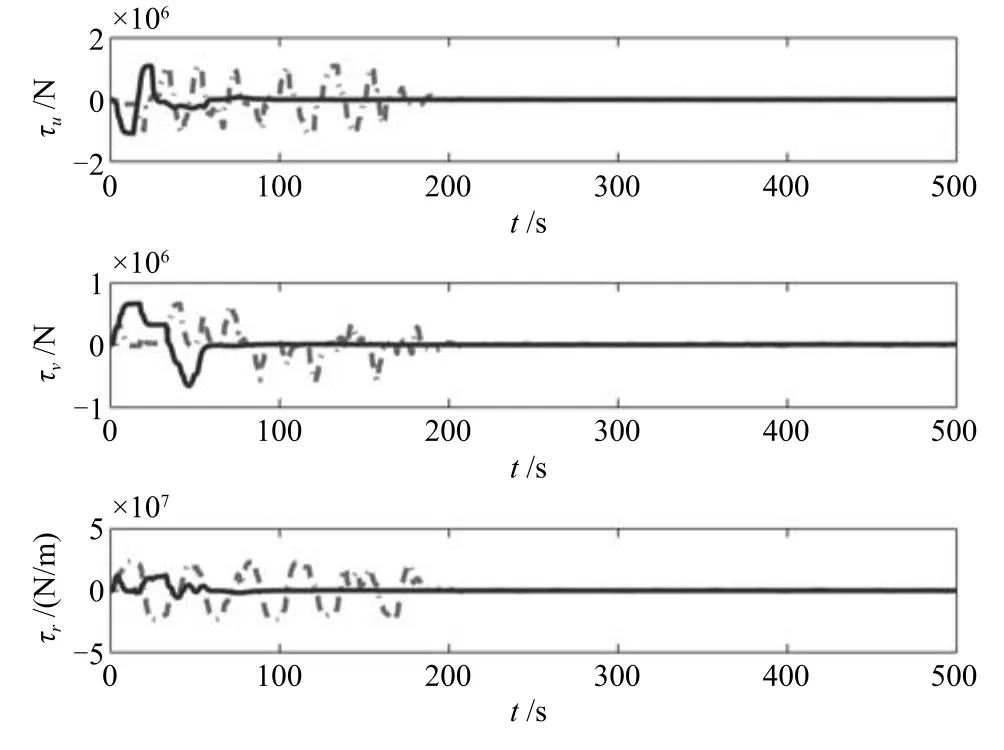
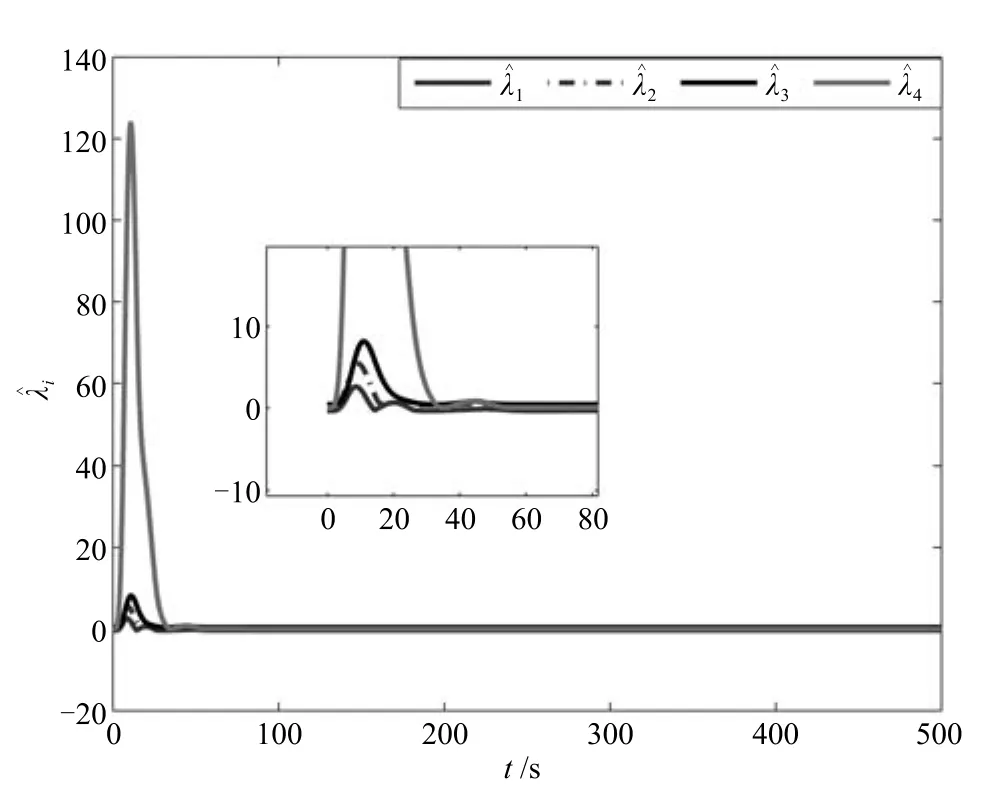
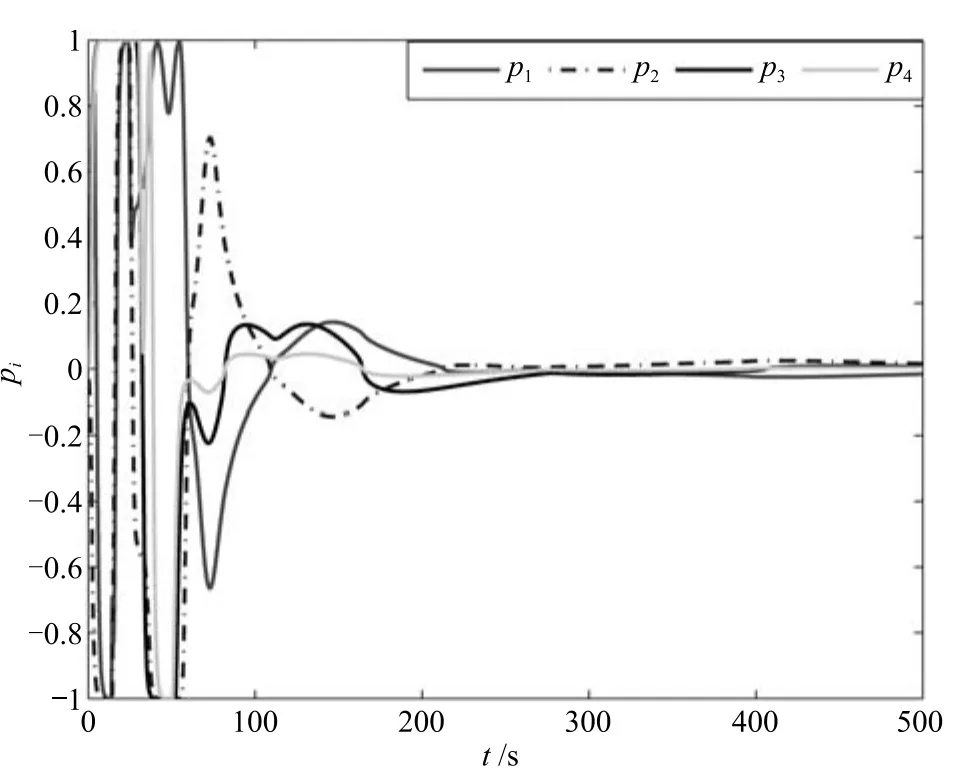
式中,χ為位置誤差的正定對稱設計矩陣,且0 步驟2.設計如下非奇異終端滑模面: 其中,p為正整數且滿足為正定的設計參數矩陣.表示向量的分數次冪 對非奇異終端滑模面(17)求導得 根據式(16)和式(18),得 第三,雷可夫和約翰遜聲稱體驗哲學不繼承任何業已發展的哲學理論,是一種全新的哲學理論[3]496,并認為由于它的創建,兩千多年來人類關于哲學的思考已成過去,哲學再不是原來的樣子[3]3。如此言過其實的話語完全忽略了馬克思主義關于思維、認識的觀點。目前,國內已有學者將體驗哲學與馬克思主義哲學觀進行了對比研究[9-10],結論是體驗哲學觀與馬克思主義認識論在許多方面有共同之處,這表明體驗哲學中的許多論點是馬克思主義認識論早已闡釋過的。如此看來,體驗哲學的觀點并不全是創新性的,說它“徹底改變了傳統的西方哲學觀”[11]是站不住腳的。 根據式(7)得: 其中, 其中,αp是控制律,的偽逆矩陣,是λ的估計值且.則非奇異終端滑模控制律設計為 Φ為待設計與狀態有關的函數.設計函數Φ為 其中,?>0. 注2.上述控制器設計時,由于在滑模面設計時引入了符號函數,必然會引起系統高頻振動,因此采用飽和函數代替符號函數消除抖動[18?19].定義飽和函數的形式如下: 其中,4為邊界層厚度. 根據文獻[20]的方法在線更新的值.相應的自適應律為 定理1.考慮執行器增益不確定問題,針對已知模型參數不確定上界和外部擾動上界的船舶動力定位系統(5),(6),(7),在終端滑模控制律(22)及自適應律(26)的作用下,船舶閉環系統內的狀態在有限時間內收斂到且保持在期望值的一個領域內. 證明.構造系統的Lyapunov函數: 將V對t求導得: 將控制律(22)和自適應律(26)代入上式,得 其中, 對于任意標量ξ0>1/2,有下列不等式成立: 由引理2可知,系統是有限時間收斂的,且系統的狀態變量會在有限時間收斂到如下穩定域內: 即滑模面的一個鄰域內: 注3.在實際海洋環境中,船舶的航行始終會受到風、浪和流的干擾,導致本文控制律下動力定位船舶的閉環系統為實際有限時間穩定,這也與文獻[21]相符合.實際上,終端滑模控制器的強魯棒性和快速收斂性可以通過增大控制器增益的方法來體現,但單一加大控制參數勢必會引起控制輸入的抖增而導致執行器過載損壞. 為了驗證設計的船舶動力定位自適應終端滑模控制器的性能,以一艘動力定位供給船為仿真對象進行仿真研究.該供給船的質量為m=4.591×106kg,長度為L=76.2m,配備有兩個主推進器和首尾側推,推進器布置如圖1所示,其中ly1=5m,ly2=?5m,lx3=25m,lx4=?25m.模型參數如下: 本文采用文獻[6]中的風、浪、流的機理模型所產生的外界環境干擾力和力矩作用于船舶模型.其中,海浪模型和風模型是耦合的,即風生浪模型.設置海洋環境干擾為6級,具體參數為:風向ψwind=45?,風速Vwind=12.5m/s,流向βcur=120?,流速Vcur=0.5m/s. 圖2~4是動力定位船舶在兩種控制律(本文有限時間控制律和文獻[8]中漸近穩定控制律)下的控制效果對比,從圖中可以看出,兩種控制器均能保持系統最終穩定狀態.圖中實線為本文控制律下的控制結果,虛線為文獻[8]中控制律下的控制結果. 圖2為供給船的平面位置(x,y)及艏向角ψ的變化曲線,仿真試驗表明,兩種控制律都能迫使供給船的空間位置和艏向角收斂于期望值,且本文所設計控制器在50s左右穩定優于文獻[8]中200s左右穩定時間,進一步實驗表明供給船在運動到期望的目標位置以后能夠保持在該期望位置附近,實現動力定位的控制目標. 圖1 供給船推進器布局圖Fig.1 Thruster configuration diagram for the supply vessel 圖2 船舶的位置和艏向角x,y,ψ歷時變化曲線Fig.2 Position and orientation variablesx,y,ψunder different control laws 圖3 船舶速度u,v,r歷時變化曲線Fig.3 The kinematic variablesu,v,runder different control laws 圖4 船舶動力定位控制律歷時變化曲線Fig.4 Curves of ship dynamic positioning control laws 圖3和圖4分別為供給船速度和控制律歷時變化曲線,得益于終端滑模控制器強魯棒性和高穩態精度的特點,可以看出在本文控制律式下,供給船的速度變量得到快速鎮定. 圖5 增益不確定估計參數1,2,3,4歷時變化曲線Fig.5 Curves of estimations for gain uncertainties1,2,3,4 圖6 執行器螺距控制輸入歷時變化曲線Fig.6 Curves of the propeller pitch of actuators 本文針對水面船舶的動力定位問題,考慮船舶在海洋工程實踐中存在的伺服系統增益不確定現象,通過對模型參數不確定和海洋環境擾動上界的估計,設計了一種自適應終端滑模控制器.利用終端滑模具有有限時間收斂、魯棒性強且收斂精度高的優點實現船舶運動學回路和動力學回路的有限時間收斂.同時對執行器的增益系數進行參數自適應,進一步得到了控制輸入為調距槳可變螺距輸入的結果.借助Lyapunov穩定性理論證明了設計的自適應終端滑模控制器是實際有限時間穩定(PFS)的;最后,以一艘配備兩個主推進器和首尾側推的供給船進行了仿真研究,仿真結果驗證了自適應終端滑模控制器的有效性.
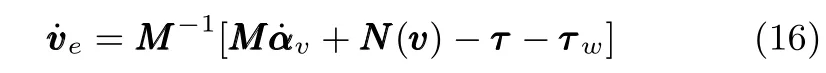
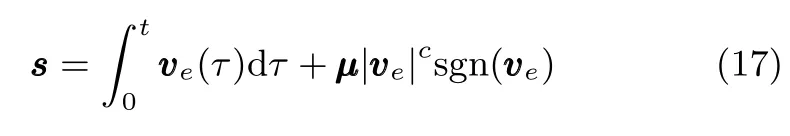

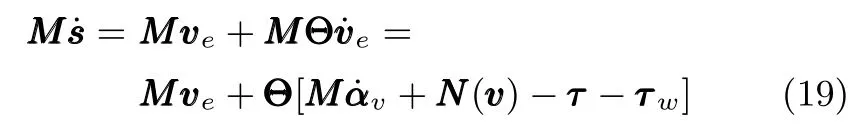
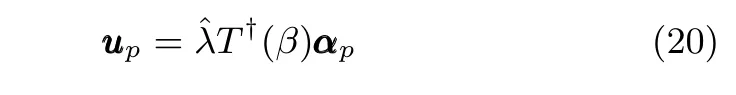
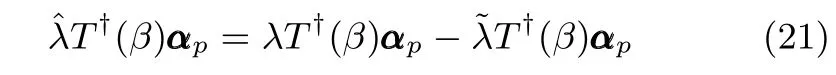
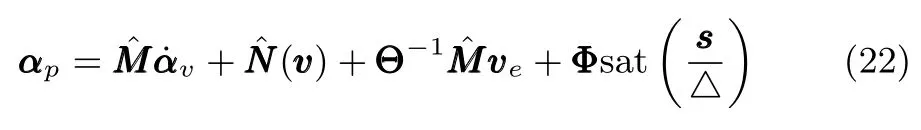
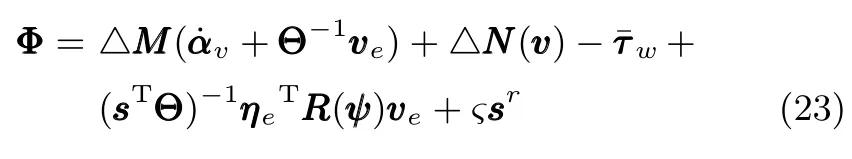


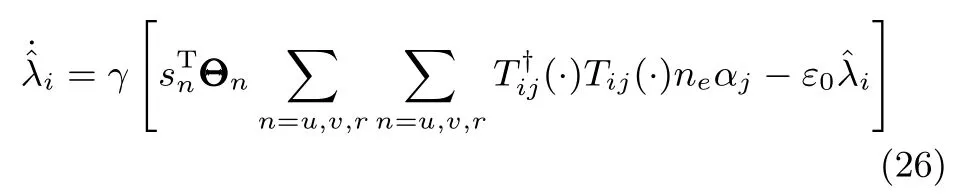
3 系統穩定性分析
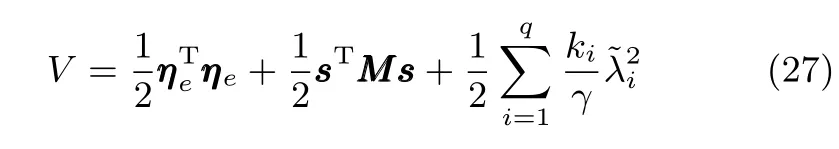
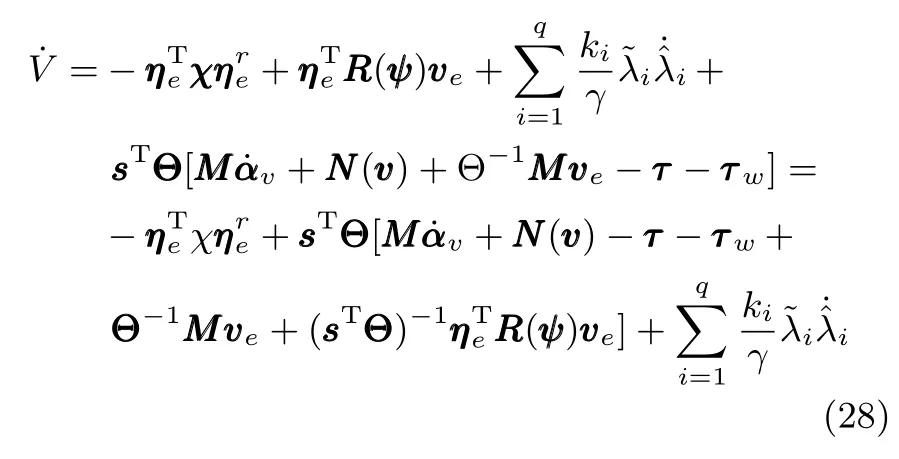
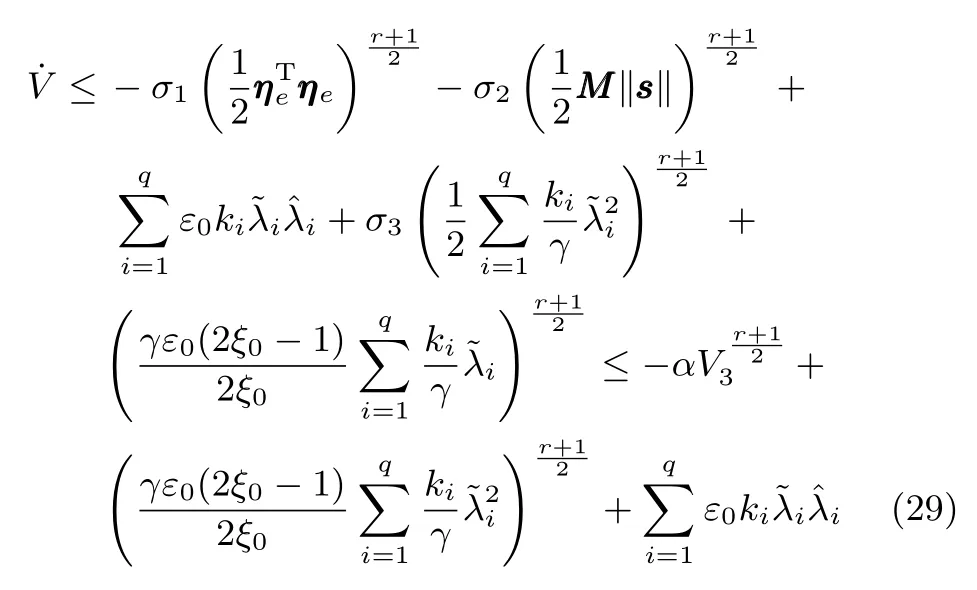
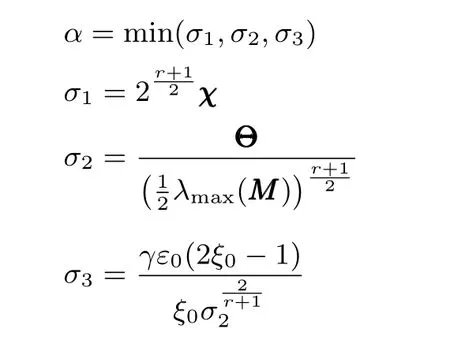


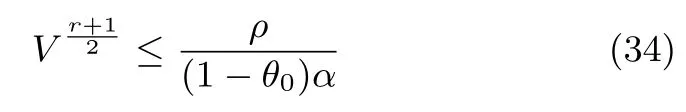
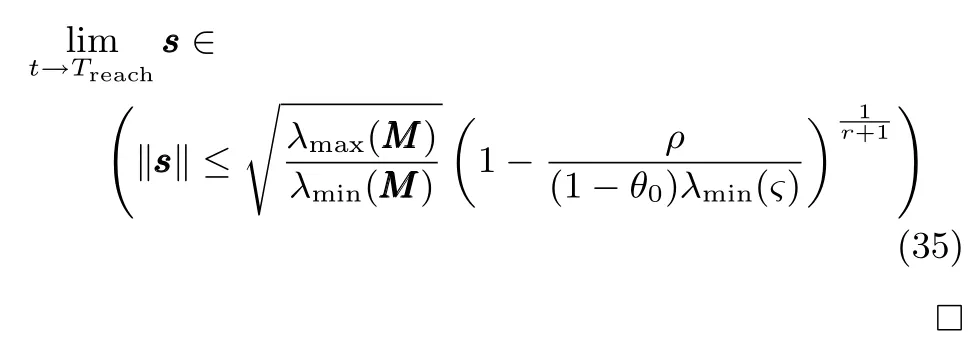
4 仿真研究
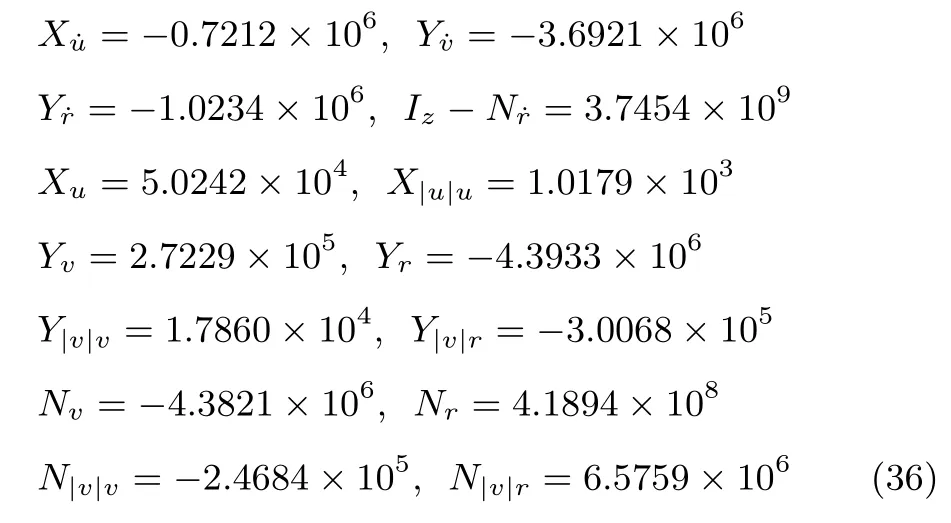
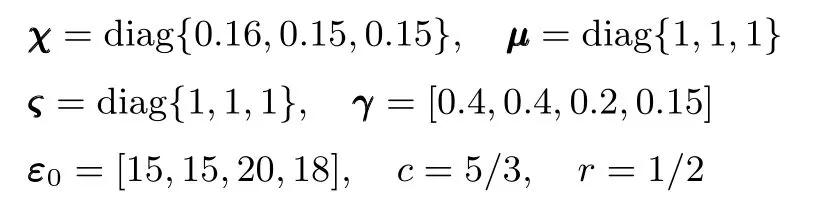
5 結論

