湍流模型和壁面函數對有障礙半開口空間氫氣燃燒模擬的影響*

李丹丹，李 敏，劉松林，羅廣南

(1.中國科學院等離子體物理研究所，安徽 合肥 230031；2. 中國科學技術大學，安徽 合肥 230026)

0 引言

氫氣是一種重要的清潔能源和化工原料，應用非常廣泛，在工業生產中(如核能發電)也可能產生大量氫氣。由于氫氣易燃易爆，在瞬間產生超壓，可能會造成嚴重的人員傷亡和財產損失，因此，對氫氣燃燒過程做出盡可能準確地預測對提高氫氣安全性具有重要意義。氫氣燃燒可能處于含有設備、管道、支架等類似障礙物結構的非密閉環境中，障礙物對氫氣燃燒能量釋放[1]和火焰傳播[2]具有重要影響，且開口處的泄壓使氫氣燃燒行為變得復雜[3]。

目前，在有障礙物半開口空間內氫氣燃燒方面，Lyu等[4]實驗研究了障礙物位置和氫氣濃度對氫氣-空氣混合氣體爆炸壓力的影響；Porowski等[5]測量了不同障礙物阻塞率、間距和氣體組分濃度下的氫氣-甲烷-空氣混合氣體的燃燒壓力和速度；Alekseev等[6]在有障礙物開口管道內開展了氫氣-空氣火焰加速和爆燃爆轟轉變(Deflagration to Detonation Transition，DDT )實驗；余立新等[7]開展了氫氣-空氣預混火焰在半開口有障礙物管道中的火焰傳播實驗研究；Gaathaug等[8]開展了氫氣-空氣混合氣體DDT實驗和數值模擬研究；Vyazmina等[9]基于2個不同點火位置的氫氣燃燒實驗進行了FLACS CFD軟件數值模擬驗證；Gamezo等[10]利用數值模擬研究了障礙物間距對預混氫氣燃燒火焰加速和DDT的影響；Li等[11]評估了不同障礙物位置、數量和間距對氫氣燃燒壓力的影響；溫小健等[12]模擬了不同的障礙物阻塞率和形狀等因素下的氫氣燃燒火焰傳播速度和壓力。綜上所述，國內外已開展的相關實驗和數值模擬研究，主要是為了考察了不同條件下氫氣燃燒壓力和火焰傳播速度，其中數值模擬驗證尚不充分，缺少湍流模型和壁面函數對數值模擬準確性影響的研究。

本文基于文獻中的實驗，利用FLUENT軟件研究湍流模型和壁面函數對有障礙物的半開口空間內氫氣-空氣預混氣體燃燒過程數值模擬結果的影響。采用了動態自適應網格加密技術，進行了網格和時間敏感性分析，確定合適的網格尺寸和時間步長，在此基礎上采用不同湍流模型和壁面函數，預測了氫氣燃燒壓力和火焰傳播行為，并將數值模擬結果與實驗結果進行了對比。

1 實驗裝置

將有燃燒壓力測量數據和火焰傳播圖像的實驗[4]作為對比，從燃燒壓力變化和火焰傳播行為2個方面考察數值模擬結果的準確性。實驗段的基本結構如圖1所示，實驗段為方形管道，尺寸為100 mm×100 mm×500 mm，底端封閉，頂端用聚氯乙烯薄膜密封。管壁為玻璃材質，以便利用高速相機拍攝火焰圖像。點火位置位于底部中心，壓力傳感器距點火位置20 mm(見圖2)。障礙物尺寸為100 mm×50 mm×10 mm，阻塞率為0.5，障礙物距離實驗段底部100 mm。

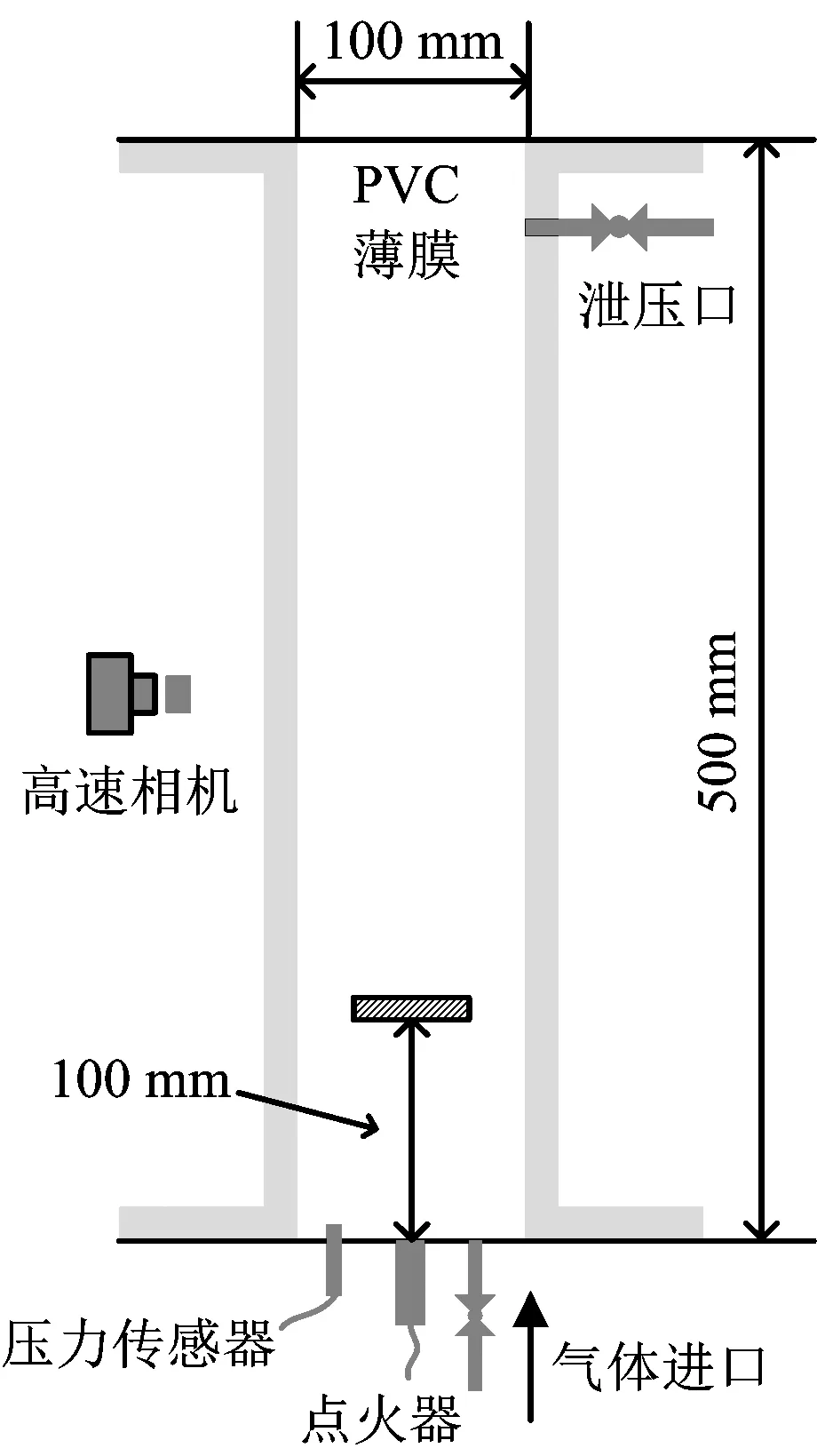
圖1 實驗段基本結構Fig.1 Schematicdiagram of experiment section

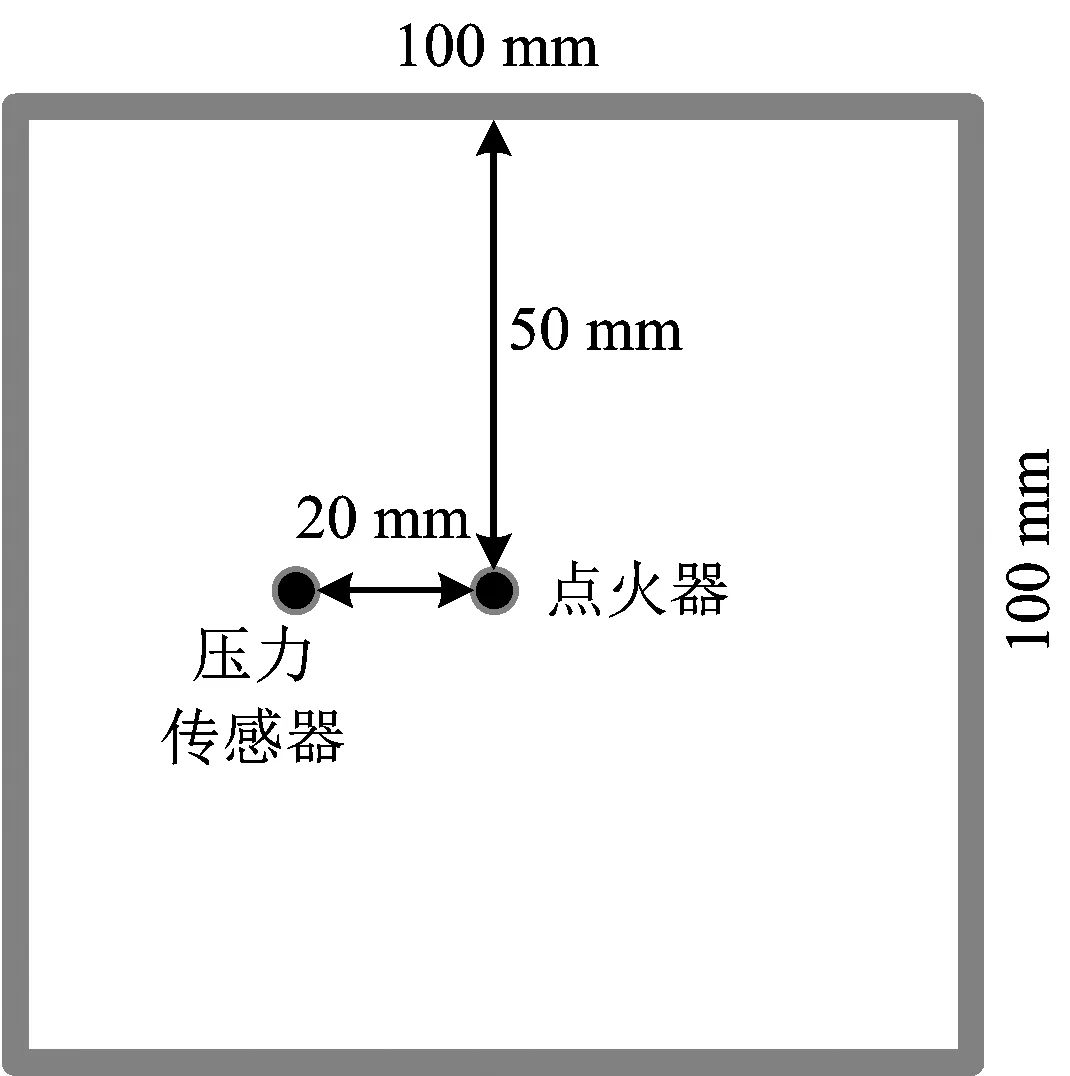
圖2 壓力傳感器位置Fig.2 Position of the pressure sensor

2 數值模擬模型及方法

2.1 幾何模型、初始及邊界條件

由于實驗段具有幾何對稱性，因此取實驗段剖面的1/2建立二維幾何模型。幾何模型被劃分成2 mm的四邊形網格，在此基礎上采用自適應網格加密技術，在數值計算過程中根據溫度梯度變化自動調整網格尺寸，以提高計算精度和效率。實驗管段中的氣體混合物由氫氣和空氣組成，其中氫氣的體積分數為29.6%。壓力監測點位置與文獻實驗中壓力傳感器位置一致。氫氣和空氣在被點燃之前混合均勻并保持靜止，初始壓力和溫度分別為0.1 MPa和298 K。由于燃燒時間很短，實驗段的所有壁面被視為絕熱，開口端被設置為無反射壓力出口邊界條件。

2.2 數值模擬方法

采用有限速率/渦耗散燃燒模型，考慮化學反應動力學與湍流混合速率對燃燒化學反應速率的影響[13-14]。壓力速度耦合采用SIMPLE算法。忽略燃燒過程中從管內燃燒產物到管壁的熱量損失。由理想氣體定律確定燃燒過程氣體混合物的密度。氣體的比熱、熱導率和粘度被定義為溫度的多項式函數。根據文獻[15]中的公式計算層流火焰燃燒速度。通過火花點火模型點燃氫氣-空氣預混氣體，假設火花初始半徑為5 mm，火花能量為0.1 J，點火持續時間為5倍時間步長。在進行網格和時間步長敏感性分析中，采用標準k-ε湍流模型和標準壁面函數。確定合適的網格尺寸和時間步長之后，考察標準、RNG和可實現k-ε湍流模型對數值模擬結果的影響。在此基礎上，選取其中最合適的湍流模型，分析標準、可伸縮和非平衡壁面函數對數值模擬結果的影響。

2.3 網格與時間步長敏感性分析

在網格自適應方案中分別設置網格加密級數為2，3和4，最小網格尺寸分別達到1，0.5和0.25 mm。圖3為網格加密級數為2時的火焰面網格，火焰面網格明顯比非火焰面區域的更密。

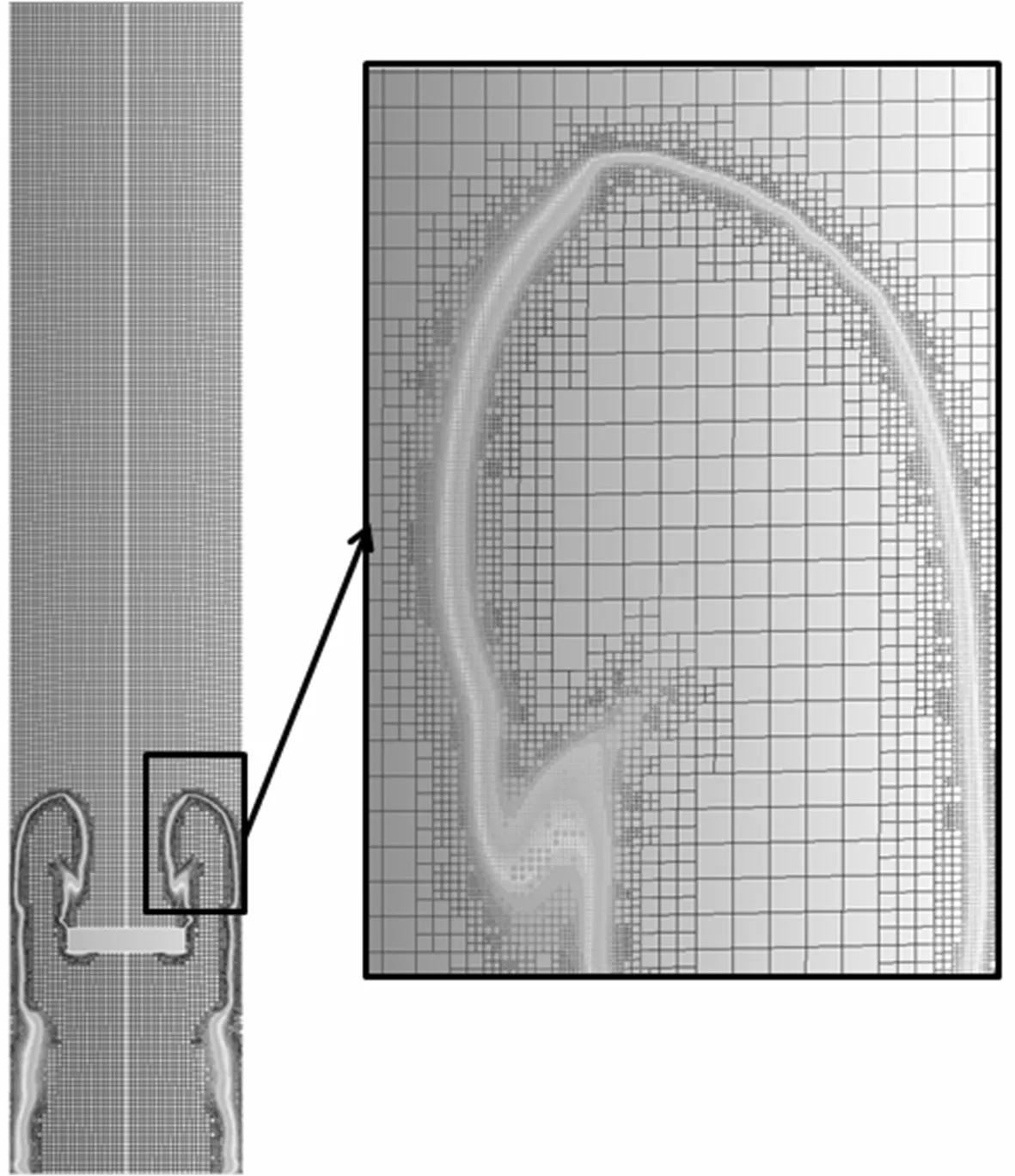
圖3 火焰面自適應網格Fig.3 Adaptive mesh of flame front

圖4為網格敏感性分析結果，與實驗值比較，通過數值模擬得到的壓力變化趨勢與測量結果都很相似，但壓力峰值出現的時間都提前了2 ms左右。數值模擬與實驗結果相比存在時間遷移現象，這在相關數值模擬[16-17]中是存在的，可能由在數值模擬中采用的點火半徑和初始湍流參數與實際值存在偏差所導致，但并不影響對壓力變化趨勢和火焰傳播行為預測結果準確性的評估。由圖4可知，當網格加密級數為2時，能夠比較準確地預測出壓力變化；當網格加密級數為3和4時，壓力峰值均增加，壓力曲線接近，說明當網格加密級數大于3時，網格尺寸對數值模擬結果的影響很小。因此，以下采用網格自適應加密級數為3。

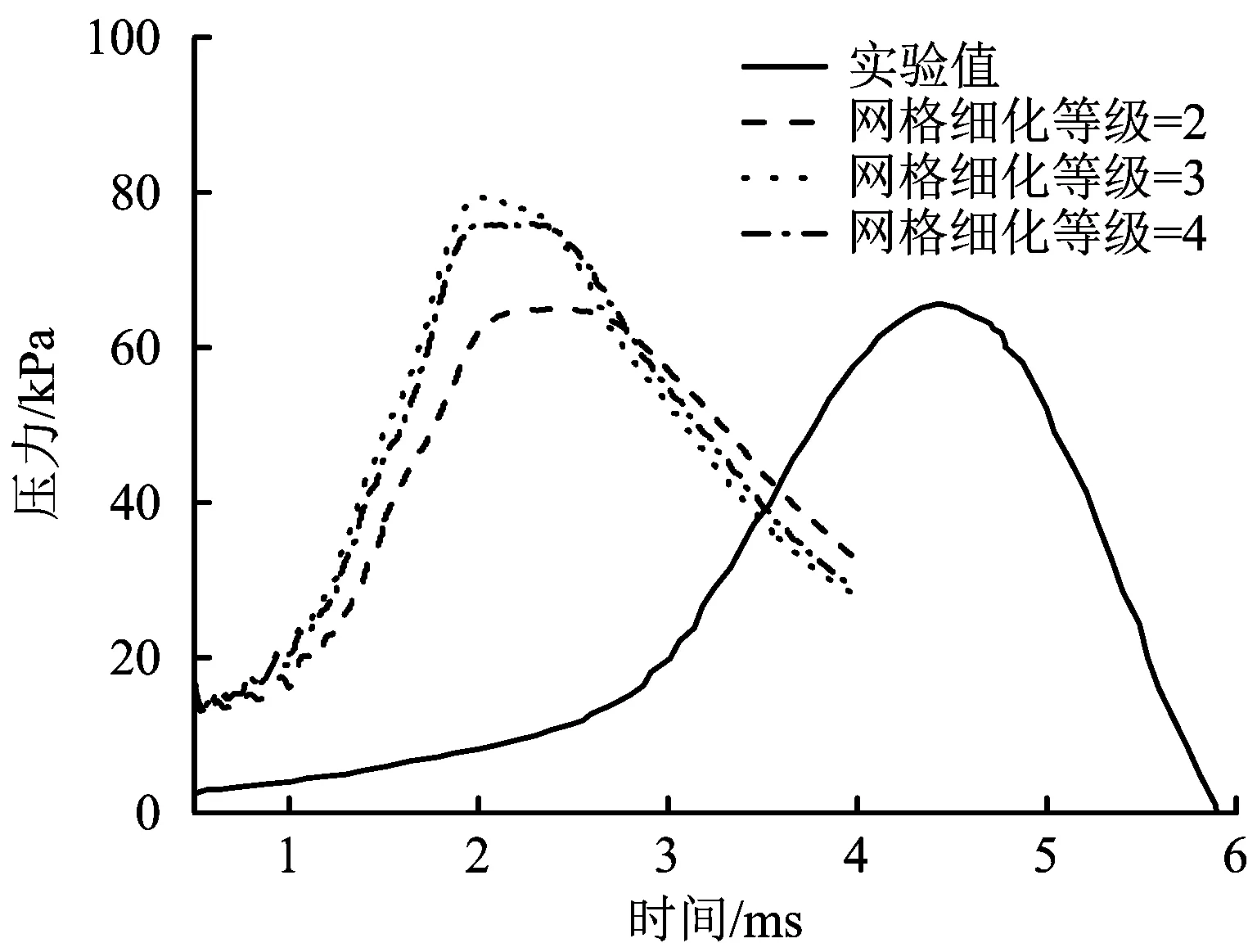
圖4 網格敏感性分析Fig.4 Grid sensitivity analysis

在時間步長敏感性分析中，時間步長Δt的范圍是4×10-7～5×10-6s，圖5為時間步長敏感性變化。由圖5可知，當時間步長為5×10-6s和3×10-6s時，壓力變化趨勢和壓力峰值與實驗值相差較大，壓力峰值比實驗測量到的壓力值分別小30.2%和10.8%，說明如果時間步長過大，數值模擬結果不準確。當將時間步長設為5×10-7s和4×10-7s時，得到的壓力變化趨勢很接近，壓力峰值僅相差2.4%，因此在以下數值模擬中時間步長都設為5×10-7s。

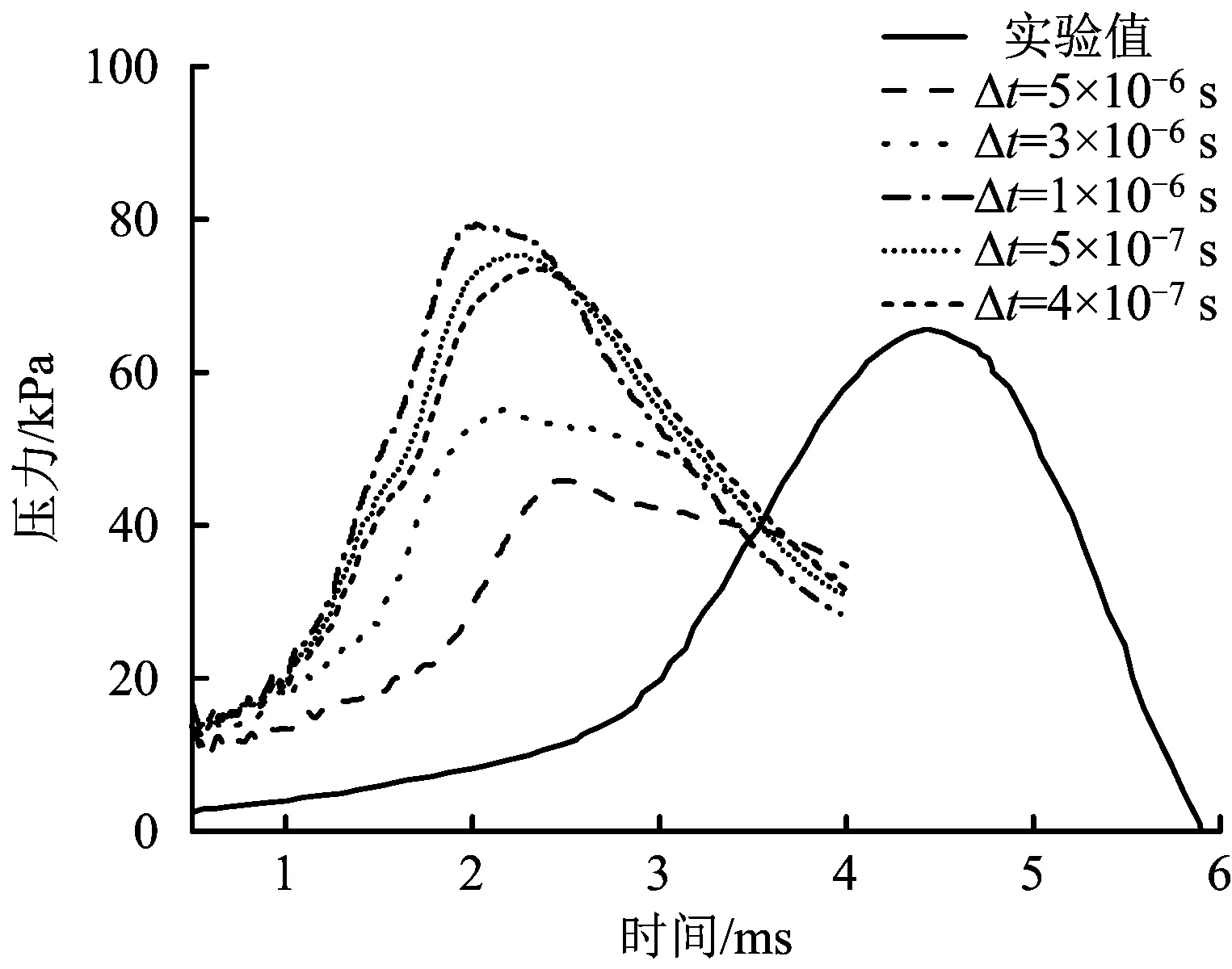
圖5 時間步長敏感性分析Fig.5 Time step sensitivity analysis

3 數值模擬結果及分析

3.1 湍流模型對數值模擬的影響

圖6為不同k-ε模型對燃燒壓力數值模擬結果的影響。其中，可實現k-ε模型對應的壓力變化趨勢與實驗結果偏離程度最大，壓力上升速度最快，壓力峰值比測量值大51.2%。標準和RNGk-ε模型對應的計算結果比較接近，壓力峰值與測量值相比相對偏差分別為14.9%和7.9%，表明由RNGk-ε模型獲得的壓力峰值與實驗值最吻合。并且，采用 RNGk-ε模型所得到壓力上升速度與實驗值最接近。

圖6 不同k-ε湍流模型對應的燃燒壓力變化Fig.6 Combustion pressure changes corresponding to different k-ε turbulent models

圖7(a)為文獻[4]給出的利用高速相機拍攝的在不同時刻下的火焰圖片，氫氣被點燃后形成半球形火焰，當火焰逐漸靠近障礙物時火焰鋒面開始變得扁平，隨后火焰從障礙物與管壁之間的空隙越過障礙物，翻越障礙物后兩側火焰鋒面開始向管中心軸卷曲，直至相互融合。圖7(b)～(d)為采用不同湍流模型進行數值模擬獲得的火焰行為。由圖7可知，與壓力變化趨勢相對應，利用數值模擬獲得的火焰行為比實驗結果提前2 ms左右。與實驗拍攝到的火焰圖像進行對比，發現如果采用可實現k-ε模型，當火焰通過障礙物與管壁之間的空隙時，火焰面很不清晰，且障礙物前的火焰區面積太小，與實驗結果差別較大；與可實現k-ε模型相比，采用標準k-ε模型計算得到火焰從障礙物兩側通過以后，火焰面向管中心傳播過程緩慢，在2 ms時，障礙物兩側火焰面的距離仍然比較大；RNGk-ε模型對應的火焰傳播行為與實驗結果吻合最好，更準確地反映了火焰受障礙物作用產生的變形和加速過程。

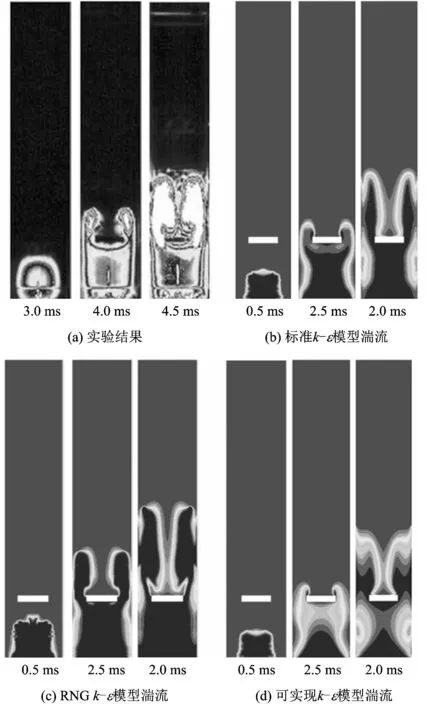
圖7 不同湍流模型下的火焰行為與實驗結果比較Fig.7 Comparison between the experimental results and the flame behaviors with different turbulence models

3.2 壁面函數對數值模擬的影響

根據湍流模型對數值模擬的影響分析結果，在分析壁面函數對數值模擬的影響時，湍流模型采用RNGk-ε模型。圖8為采用不同壁面函數進行數值模擬所獲得的燃燒壓力與時間的關系，可以看出，標準和可伸縮壁面函數對應的結果很接近，如果采用非平衡壁面函數，在壓力上升階段壓力值稍微變大。可伸縮、標準和非平衡3種壁面函數對應的壓力峰值逐漸增加，與實驗值相比較，壓力峰值相對偏差分別為1.7%，7.9%和13.4%，可伸縮壁面函數的壓力峰值與實驗值最接近。圖9為不同的壁面函數下的火焰行為與實驗結果對比，對于火焰傳播過程，如果采用非平衡壁面函數，火焰翻越障礙物后的傳播速度比標準和可伸縮壁面函數的更快，使火焰形狀顯得更加細長。標準和可伸縮壁面函數對應的火焰行為基本一致，也與實驗拍攝到的火焰行為較為吻合。

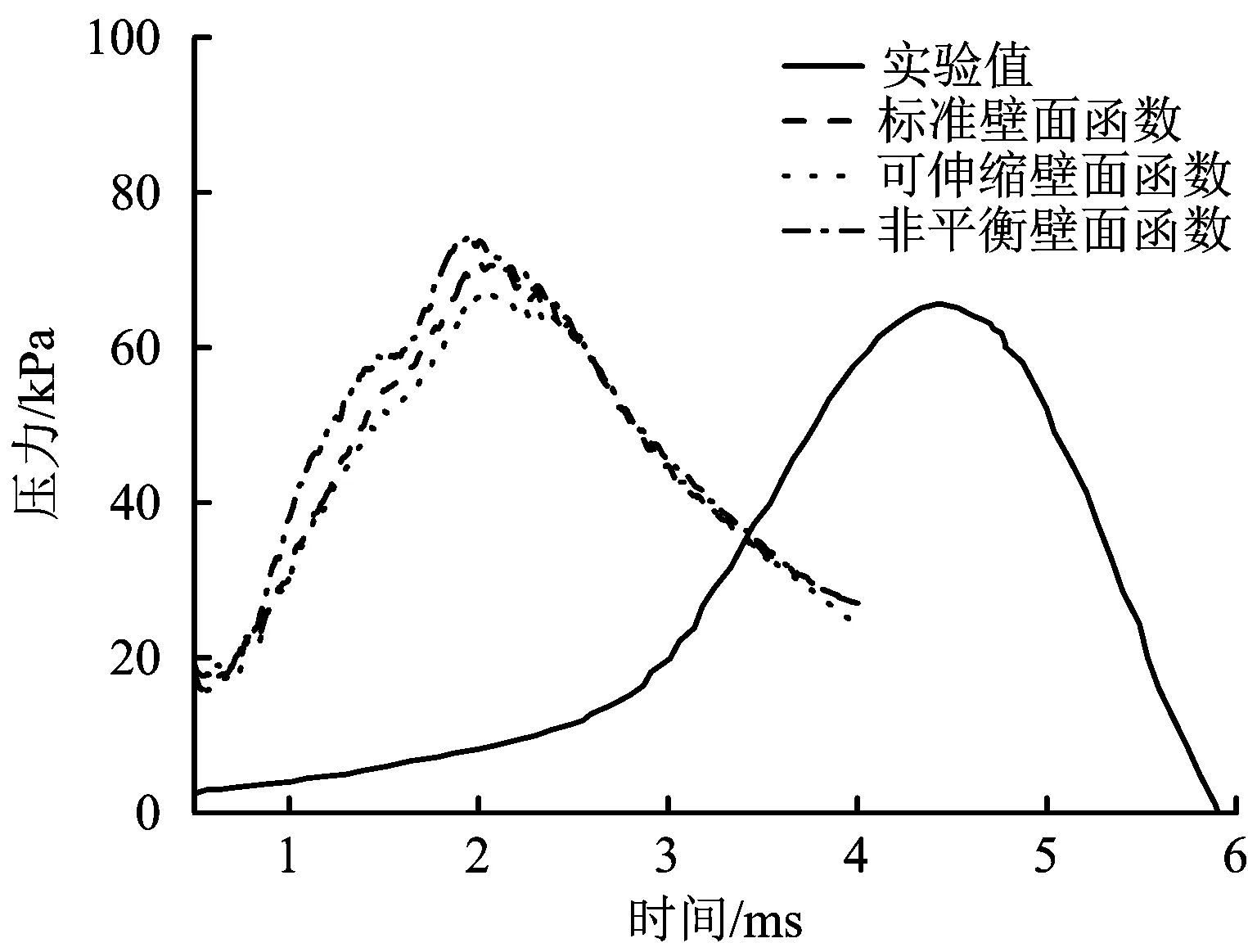
圖8 不同壁面函數對應的燃燒壓力變化Fig.8 Combustion pressure changes corresponding to different wall function

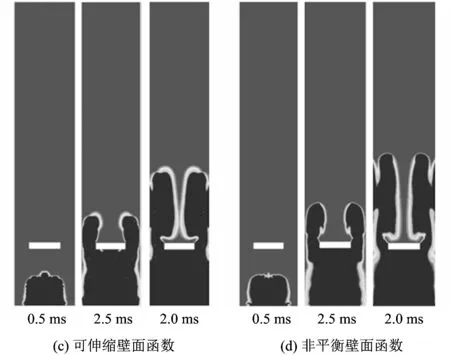
圖9 不同的壁面函數下的火焰行為與實驗結果對比Fig.9 Comparison between the experimental results and the flame behaviors with different wall functions

4 結論

1) 標準k-ε模型基本可以比較準確地預測出火焰燃燒壓力變化和火焰傳播行為。RNGk-ε模型考慮了湍流旋渦，數值模擬結果更準確。可實現k-ε模型使燃燒壓力值和火焰形狀與實際情況相比偏差較大。

2)利用標準壁面函數和可伸縮壁面函數預測出的火焰行為與實驗結果都很吻合，但非平衡壁面函數對被障礙物擾動的火焰有比較明顯的加速，使火焰形狀與實際情況不符。從燃燒壓力上看，可伸縮壁面函數的壓力峰值與實驗值最接近，非平衡壁面函數的壓力峰值與實驗值相比偏差最大。