RV減速器動力學特性研究

趙海鳴，聶 帥，朱加云，蔡進雄

(1.中南大學 機電工程學院，湖南 長沙 410083； 2.中南大學 高性能復雜制造國家重點實驗室，湖南 長沙 410083； 3.湖北三江航天萬峰科技發展有限公司，湖北 孝感 432000)

0 引言

RV(Rotate Vector)減速器是20世紀80年代由日本最先研發并投入使用的減速傳動裝置，具有傳動比大、剛度強、回差小等優勢，在工業自動化以及航空航天等科技領域得到廣泛應用[1-4]。RV減速器主要應用在機器人大臂或底座等高負載關節，該工況下對RV減速器的剛度及精度要求很高，因此研究RV減速器的動力學特性十分必要。本文擬對RV減速器整機的動力學特性進行研究，并完成關鍵零部件的模態分析，為RV減速器結構的優化及綜合性能的提升奠定基礎。

1 RV減速器動力學模型的建立

RV減速器原理圖如圖1所示，它是兩級封閉差動輪系減速傳動裝置，第一級傳動為漸開線齒輪傳動，第二級傳動為擺線針輪傳動[5]。

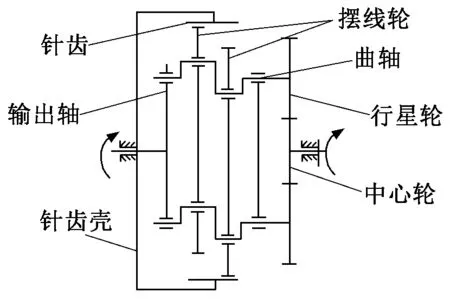
圖1 RV減速器結構原理圖

本文以RV160-E為例建立其動力學模型。在第一級減速機構中，將行星輪與中心輪嚙合部分等效為彈簧連接模型，而剩下的部分則等效為集中質量。在第一、二級減速機構間，通過花鍵分別將行星輪與相應的曲柄軸一端部連接，將二者等效為一體；將曲柄軸與行星輪嚙合部分等效為彈簧連接；而剩下的部分則等效為集中質量。在第二級減速機構中，將擺線輪與針齒嚙合部分等效為彈簧連接，而剩下的部分則等效為集中質量。RV減速器動力學模型如圖2所示。

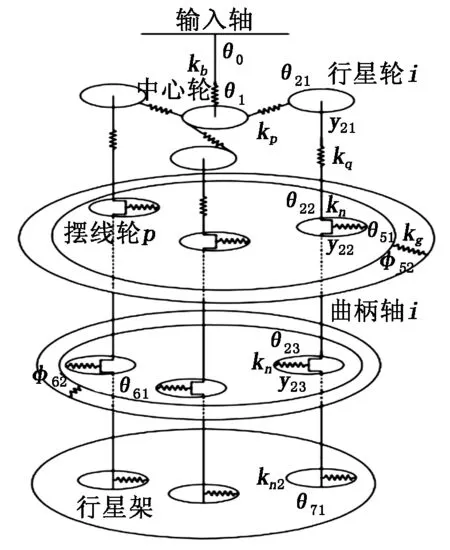
圖2 RV減速器動力學模型

圖2中，漸開線齒輪的嚙合剛度為kp，擺線針輪的嚙合剛度為kg，輸入軸的扭轉剛度為kb，曲柄軸的扭轉剛度為kq，偏心軸承的剛度為kn，支撐軸承的剛度為kn2；中心輪的基圓半徑為rb，行星輪的基圓半徑為rp，曲柄軸分布圓半徑為rh，擺線輪節圓半徑為rc；偏心距為a；θ21、θ22、θ23、y21、y22、y23分別為曲柄軸2在行星輪、兩偏心處的扭轉角和線位移，J21、J22、J23、m21、m22、m23分別為曲柄軸2在行星輪、兩偏心處的轉動慣量和質量，其余曲柄軸同理；θ51、φ52分別為擺線輪1自轉與公轉的扭轉角，J51、J52分別為擺線輪1自轉與公轉的轉動慣量，擺線輪2同理；θ71、J71分別為行星架的扭轉角和轉動慣量。

1.1 漸開線齒輪傳動輪系動力學模型的建立

輸入軸傳遞轉矩過程中，設k0為輸入軸扭轉剛度，J0為輸入軸的轉動慣量，θ0為輸入軸振動扭轉角度，θ1為主動漸開線齒輪的振動扭轉角度，則輸入軸的振動方程為：

(1)

其中：Tin為RV減速器的輸入轉矩。

設α1為漸開線齒輪嚙合角，k1、J1分別為主動漸開線齒輪的嚙合剛度和轉動慣量，則其振動方程為：

J1θ1=k0(θ0-θ1)+k0(θ21rp+y21cosα1-θ1rb)rb+k1(θ31rp+
y31cosα1-θ1rb)rb+k1(θ41rp+y41cosα1-θ1rb)rb.

(2)

1.2 曲柄軸動力學模型的建立

設曲柄軸受到偏心軸承在切向方向的支持力分別為FAt與FDt，曲柄軸端部受到的行星輪嚙合力為F[6]，曲柄軸受力情況如圖3所示。

設曲柄軸結構的廣義坐標為：

{θ21，θ22，θ23，θ31，θ32，θ33，θ41，θ42，θ43，y21，y22，y23，
y31，y32，y33，y41，y42，y43}.

相對應的質量矩陣為：

{J21，J22，J23，J31，J32，J33，J41，J42，J43，m21，m22，
m23，m31，m32，m33，m41，m42，m43}.

故曲柄軸2的動力學方程為：

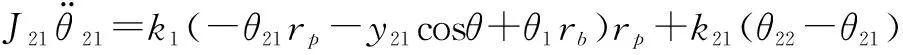
(3)

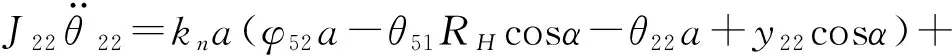
(4)

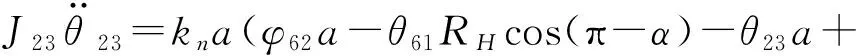
(5)

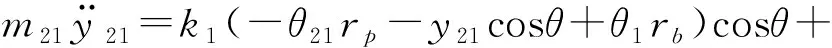
(6)

(7)

(8)

其中：α為曲柄軸扭轉角；RH為偏心軸承分布圓半徑；k21、k22為曲柄軸的扭轉剛度。

圖3 曲柄軸受力分析圖情況

1.3 擺線輪動力學模型的建立

取擺線輪的廣義坐標為{θ51，θ61,φ52,φ62}，相對應的質量矩陣為{J51,J61,J52,J62},則擺線輪1的動力學方程為：

(9)

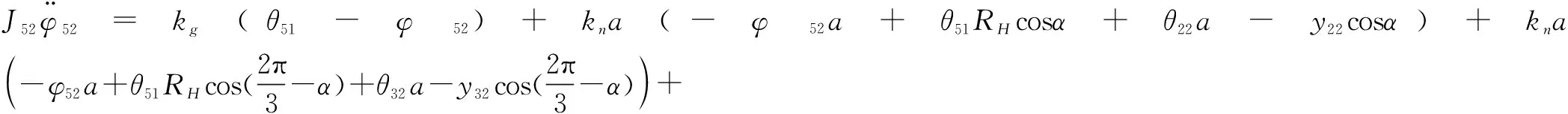
(10)

1.4 行星架動力學模型的建立

行星架在曲柄軸公轉運動的作用下進行自轉運動。設支撐軸承分布圓半徑為RL，行星架的動力學方程為：

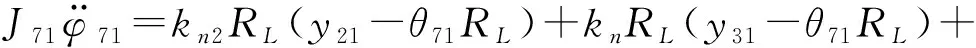
(11)

2 RV減速器動力學模型的求解

系統動力學模型的求解即固有頻率的求解是動力學分析匯總的基本內容[7]。系統動力學方程可描述為：

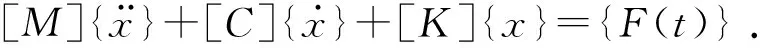
對應的特征方程為：

([K]-ω2[M]){x}=0.

其中:ω為系統的固有頻率。

計算ω只需在MATLAB上調用函數:[V,D]=eig(K,M)。

本文建立的系統剛度矩陣如下：

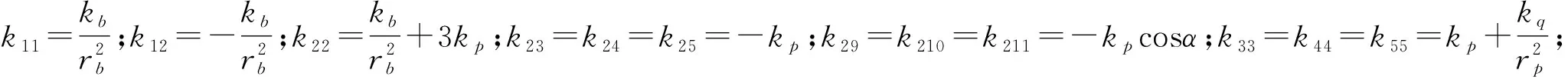
其中的β為曲柄軸兩個偏轉軸線平面和曲柄軸、擺線輪中心軸線平面的夾角。

系統質量矩陣如下：

2.1 軸類扭轉剛度計算

圓柱軸扭轉剛度的表達式為：

(12)

其中:G為彈性剪切模量；Ip為極慣性矩；l為軸長。

階梯軸扭轉剛度計算公式如下：

(13)

其中:ki為第i段軸的扭轉剛度。

輸入軸為齒輪階梯軸，可忽略軸端齒輪的影響，將其等效為階梯軸，結構尺寸如圖4所示。

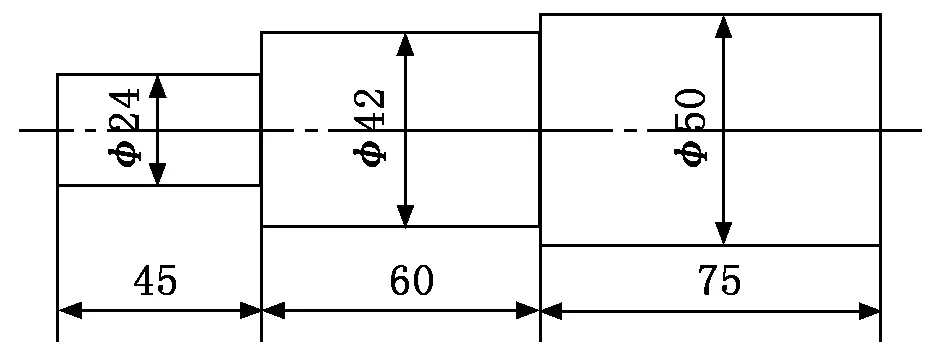
圖4 輸入軸結構尺寸

曲柄軸可直接按照圓軸扭轉剛度公式計算，此處軸徑為Φ20 mm、長度為65 mm。

將相關數據代入式(12)和式(13)可得輸入軸的扭轉剛度和曲柄軸的扭轉剛度分別為47 054 N·m/rad、19 333 N·m/rad。

2.2 軸承剛度計算

滾動軸承剛度計算公式為[8]：

(14)

RV減速器的軸承主要有偏心軸承及支撐軸承，基本參數如表1所示。

表1 軸承基本參數

將相關數據代入式(14)可得偏心軸承剛度和支撐軸承剛度分別為1.02×109N/m、8.175×108N/m。

2.3 漸開線齒輪嚙合剛度計算

齒輪嚙合剛度的表達式如下[9]：

cr=(0.75εα+0.25)c′.

(15)

其中:εα為齒輪端面重合度，εα=1.568；c′為單對齒嚙合剛度，c′=1.29×108N/m。

由式(15)計算可得漸開線齒輪的嚙合剛度為1.846×108N/m。

2.4 擺線針輪嚙合剛度計算

擺線針輪接觸模型如圖5所示，擺線針輪整體嚙合剛度不是各個單齒嚙合剛度單純疊加[10]。

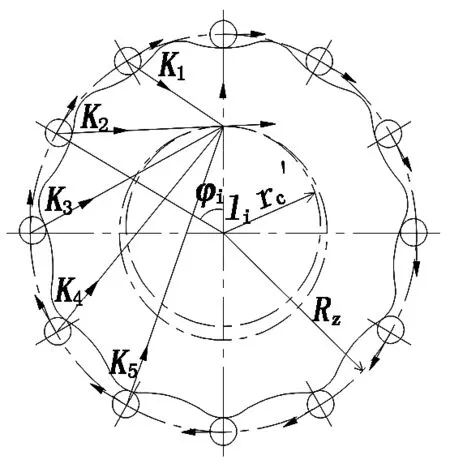
圖5 擺線針輪接觸模型

實際應用中擺線輪與針齒同時嚙合齒數將少于總齒數的一半[11]，因此在疊加計算擺線針輪整體等效扭轉剛度時加入調整系數λ(一般取λ為0.6～0.7)。擺線針輪整體等效扭轉剛度表達式為：

(16)

其中:zb為擺線輪齒數;Ki為第i個針齒與擺線輪接觸的剛度；li為第i個針齒嚙合點的公法線至擺線輪中心的距離。

由式(16)計算可得擺線輪等效扭轉剛度為5.159×105N·m/rad。

2.5 RV減速器固有頻率計算

通過本文建立的剛度、質量矩陣，利用MATLAB得到的RV減速器前10階固有頻率如表2所示。

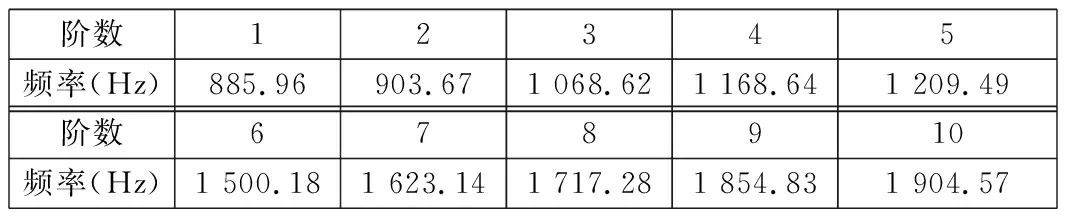
表2 RV減速器前10階固有頻率

系統固有頻率只取決于系統的剛度與質量，從總體上看，不論單自由度系統還是多自由度系統，都遵循系統質量增大、剛度減小降低系統固有頻率這一規律，因而研究關鍵零部件的動態特性不僅可以反饋整機的動態特性，還可以優化整機結構。

3 RV減速器關鍵零部件有限元模態分析

本文對RV減速器關鍵零部件進行模態分析，計算出關鍵零部件擺線輪、曲柄軸和行星輪的固有頻率及相應振型，以避免共振和有害振型的出現。RV減速器各關鍵零部件材料參數如表3所示。

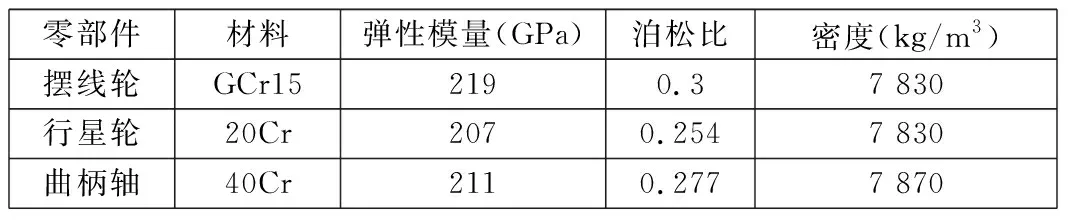
表3 各關鍵零部件材料參數

3.1 擺線輪的模態分析

邊界條件設置：在擺線輪中心孔添加圓柱面約束，約束徑向及軸向位移，保證其繞中心孔軸線的旋轉自由度。進行模態分析求解出擺線輪的前10階固有頻率，如表4所示。

由表2和表4可知，系統的第2、第3、第5階固有頻率與擺線輪的第3、第4、第5階固有頻率比較接近，可適當提高擺線輪的剛度來避開共振區域。

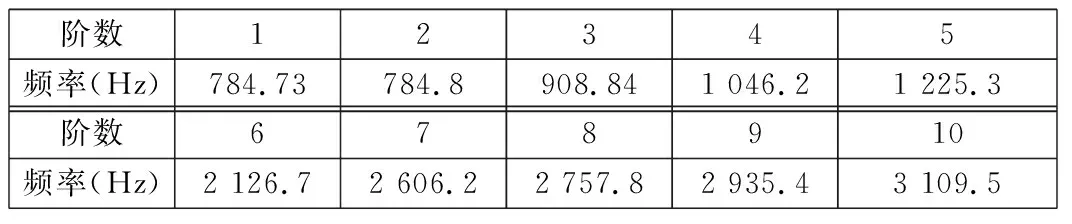
表4 擺線輪前10階固有頻率

3.2 曲柄軸的模態分析

邊界條件設置：在4個圓軸段表面添加圓柱面約束，約束軸向及徑向位移，保證偏心和同心部分的旋轉自由度。進行模態分析求解出曲柄軸的前10階固有頻率，如表5所示。

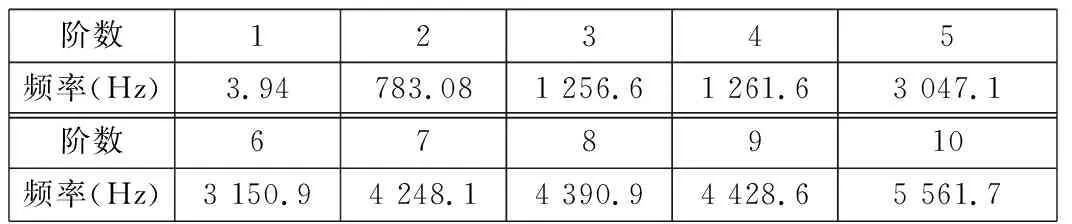
表5 曲柄軸前10階固有頻率

曲柄軸的第3、第4階固有頻率與系統的第5階固有頻率比較接近。同樣地，可適當改變行星輪的質量和曲柄軸的剛度來避開共振區域。觀察振型圖(見圖6)可知，最大位移集中發生在行星輪與曲柄軸嚙合處，這對嚙合處的剛度有了一定要求并且為曲柄軸的優化設計提供了參考依據。

圖6 曲柄軸第2階、第6階振型

4 結論

綜合考慮RV減速器工作過程中的各影響因素，建立了十六自由度的RV減速器整機動力學模型，根據牛頓定律和廣義坐標法建立了關鍵零部件的動力學方程。利用MATLAB計算出系統的固有頻率及相應振型。利用ANSYS Workbench對主要零部件進行了模態分析，得到了它們的固有頻率和振型，分析表明擺線輪的固有頻率不在整機的固有頻率點上。觀察振型圖顯示應提高曲柄軸嚙合處的剛度，為曲柄軸的優化設計提供了參考依據。