考慮性別偏好影響的通勤合乘匹配模型*

何勝學 程 龍 陳經緯 杭佳宇

(上海理工大學管理學院 上海 200093)

0 引 言

車輛合乘一般將現實中司乘匹配時所考慮的時間、起訖點、費用限制等作為約束，以消耗最小出行成本滿足最多的出行需求為目標建立模型[1].車輛合乘模型廣泛應用于殘疾人和老年人的門對門接送[2]或是校車路線規劃[3].現在隨著“共享”理念推廣及移動智能終端的普及，車輛合乘進一步發展為出租車合乘[4]與通勤車輛合乘[5].通過對比合乘和公交的效用差值，畢笑天等[6]對市民出行方式選擇進行研究，確定了合乘出行和公交出行的選擇依據.在假設司機在新模式下可以以一定代價“購買”其他司機的乘客條件下，Roger等[7]對司乘匹配FCFS(first-come, first-served)模式進行了改進，發現加入乘客交換機制后，整個合乘系統的服務水平得到顯著提高.聶昌成等[8]以寧波市為例提出了基于電召平臺的出租車合乘模式，并對此合乘模式中的乘客運送以及計費和收益進行了初步分析.

國內外學者對車輛合乘路徑規劃、費率、車輛調度以及模型算法等領域[9-12]研究較多，較少涉及乘客的合乘偏好等行為決策研究.現實中乘客出于安全等因素的考慮會對合乘者性別進行選擇，進而考慮選擇是否進行合乘.Yan等[13]在使用時空網絡處理出租車的路徑規劃問題時，將出租車分為普通出租車和只接受女乘客出租車，更加貼近現實中乘客對出租車安全性的需求.程杰等[14]以出租車合乘為背景建立動態車輛合乘模型，并在模型中將出租車和乘客進行了劃分，以性別作為車輛和乘客匹配的依據.但上述文獻僅考慮固定的乘客組劃分，沒有考慮現實合乘中存在不同的性別合乘需求以及乘客性別占比變化對合乘匹配效果的影響.針對上述問題，文章對通勤車輛合乘匹配中乘客性別因素的影響進行深入研究.

1 模型說明

1.1 參數說明

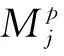
z(i,J,(k,g))為司機i與乘客組J可行匹配，通勤乘客上車點和下車點為(k,g)；z0為司機不進行合乘；Z為所有匹配集合.當司機i與乘客組J滿足匹配約束時，即z(i,J,(k,g))匹配成功時會產生一組數據(υz,σz)；υz為此次合乘匹配中參與的司機與乘客總人數；σz為合乘給通勤走廊中帶來的機動車行駛距離優化值，σz=doidi-(doik+dkg+dgdi)+∑j∈J(dojdj-(dojk+dgdj)).式中：doidi-(dk+dkg+dgdi)為司機i在合乘過程中產生的繞行距離；dojdj-(dojk+dgdj)為乘客j參與合乘后走廊中機動車行駛距離優化值.如果σz>0，則表示進行z(i,J,(k,g))匹配時合乘使得通勤走廊中機動車行駛距離優化值為正，此次合乘是有意義的.

1.2 目標函數

一般可考慮如下通勤合乘匹配的優化目標：①方便通勤者在通勤時段出行，即使得通勤時間段內走廊中最多的司機和乘客(υ值)參與到合乘中來;②最大程度的緩解通勤走廊中交通壓力，即使通勤走廊中機動車行駛距離優化值(σ值)最大.

對應上述目標建立的兩個目標函數為

(1)

(2)

式中：xiz和xjz為司機與乘客匹配的0-1決策變量.當司機i進行z(i,J,(k,g))匹配時，xiz取1；反之xiz取0.當乘客j∈J進行z(i,J,(k,g))匹配時，xjz取1；反之xjz取0；Jz為z匹配中所有參與乘客的集合；υz為此次z合乘參與的人數，包括司機與所有乘客.

式(1)和(2)分別為模型的目標是通勤合乘參與者數值最大和通勤走廊中機動車行駛距離優化值最大.

1.3 約束條件

模型基本約束為

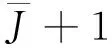
≤Ci

(3)

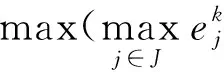
(4)

toik+τ+tkg+tgdi≤Ti

(5)

(6)

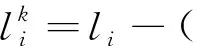
(7)

(8)

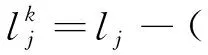
(9)

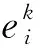
現實中乘客在與其他合乘者合乘時，會出于自身安全等原因考慮對其他合乘者的性別進行選擇.為了全面的描述合乘性別模式，下面針對不同模式下乘客的性別合乘偏好給出相應的模型約束條件.

第一種合乘模式為偏好同性乘客之間進行合乘.假設在這種合乘模式下通勤乘客只偏好和同性的乘客進行合乘.上述偏好同性合乘的模式可表示為

,?z∈Z,Jz∈zm,

?z∈Z,Jz∈z

(10)

(11)

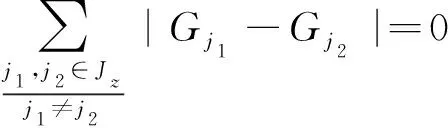
(12)

(13)

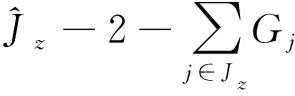
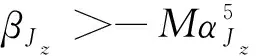
(14)

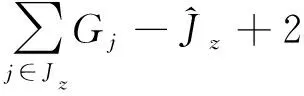
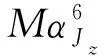
(15)

當乘客組J中僅有一位乘客時，此乘客不受性別合乘模式的約束，此時βJ取值為1，對應約束如下式.

(16)

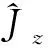
當對乘客組內乘客性別是否滿足合乘模式進行判斷后，模型需要對滿足匹配要求的乘客組和通勤司機進行決策變量賦值.即當乘客組滿足性別合乘模式要求或乘客組內容忍系數不小于控制系數時，對應參數xiz和xjz賦值為1；否則賦值為0.約束如下式.

(17)

(18)

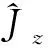
,?i∈D

(19)

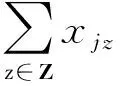
(20)

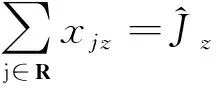
(21)

式(19)為模型中任意司機只能參與到一個合乘匹配中，包括z0.式(20)為模型中任意乘客j只能參與一個匹配中即∑z∈Zxjz=1或不參與匹配即∑z∈Zxjz=0.式(21)為對于?z∈Z，只有匹配z中所有的乘客參與者都參與到z匹配中時，匹配z才是有效的.其中xiz和xiz分別為0-1決策變量.

2 求解算法

司乘匹配約束中有非線性約束條件，因此所建通勤匹配模型為非線性整數規劃模型.以通勤中合乘匹配的具體實現過程為基礎，本文設計一種求解上述模型的啟發式求解算法.新算法首先確定可行匹配集，然后計算各匹配相關特征量，最后利用分層法確定最佳合乘匹配.新算法不僅可以有效處理模型的非線性約束，而且實現的復雜度較低.

新算法首先將整個路網中所有司機和乘客進行匹配，進行時間、距離和性別約束處理后統計所有可行匹配Z并計算Z中υZ值和σZ值.根據可行匹配z賦值對應控制變量(xjz和xiz)并進行最終模型計算，司機與乘客在無約束下匹配結果見圖1.圖中有兩位司機d1和d2，兩位乘客p1和p2.z0為司機沒有搭載乘客.兩位司機可以選擇單獨搭載乘客p1，即圖中z1和z4的匹配結果；選擇單獨搭載乘客p2，即圖中z2和z5的匹配結果；或是一同搭載乘客p1和p2，即圖中z3和z6的匹配結果.

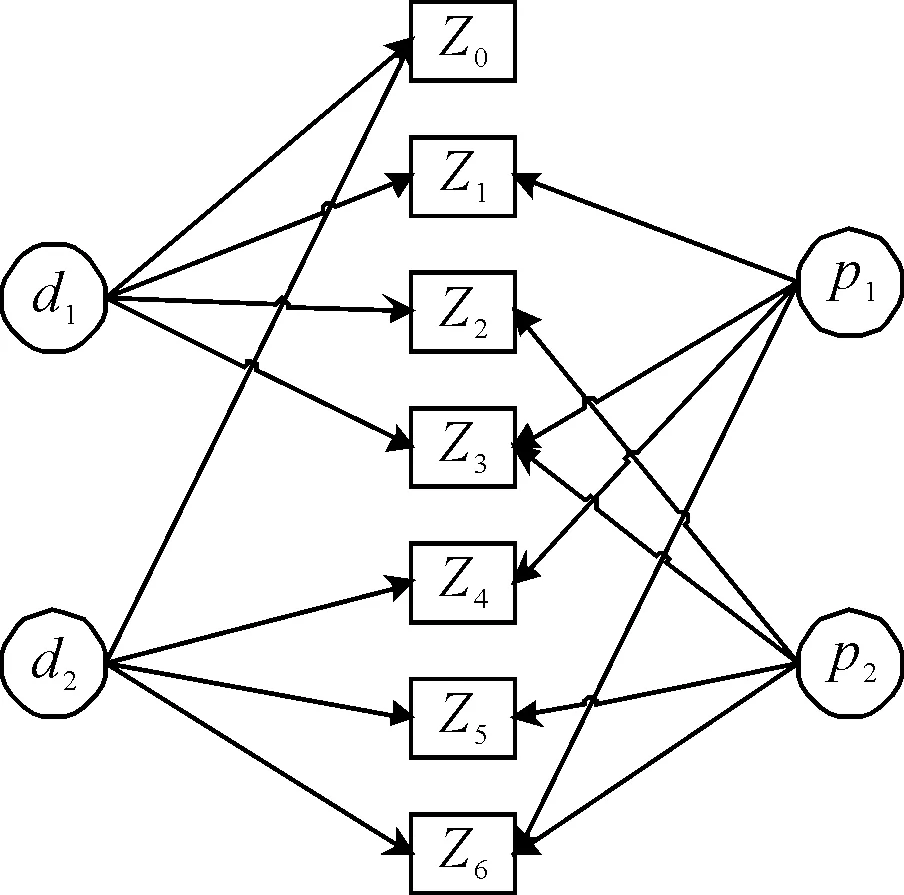
圖1 司機乘客匹配結果圖

圖2為司機乘客匹配結果優化圖，由圖2可知，有些通勤司機乘客的匹配已經因為不符合約束而不存在，例如司機d2不能一同搭載乘客p1和p2.圖中數字為每組通勤司機乘客匹配所產生的兩個數據，在模型中用(υz,σz)表示.其中：υz為此次合乘匹配中參與的司機與乘客總人數；σz為此次合乘匹配通勤走廊中產生的行駛距離優化值.當司機d1和d2不參與合乘時就不會產生對應的(υ,σ)，即d1和d2到z0之間數據都為0.

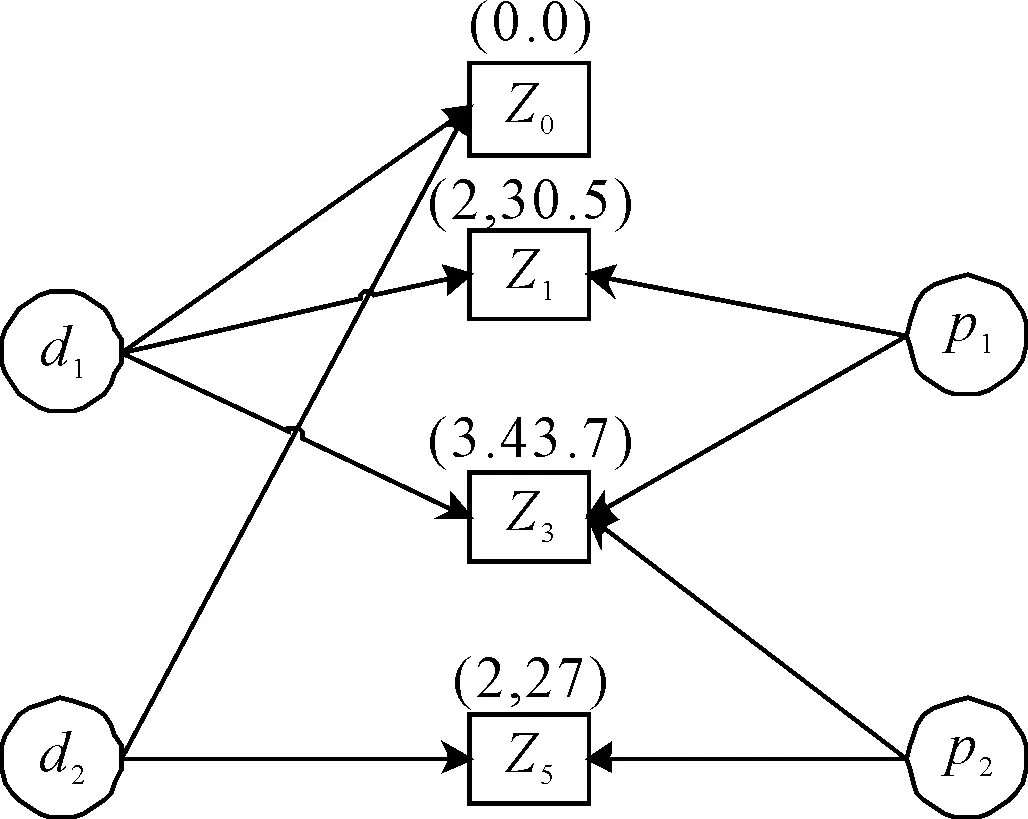
圖2 司機乘客匹配結果優化圖

針對上文提出的合乘匹配模型，本文設計了三步驟求解算法,如下所示.

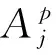
步驟2計算可行匹配z對應的(υz,σz).可行匹配z(i,J,(k,g))∈Z中信息包括司機i與乘客組J和合乘的上車點下車點(k,g).由式σz=doidi-(doik+dkg+dgdi)+∑j∈J(dojdj-(dojk+dgdj))計算出對應走廊中機動車行駛距離優化值σ以及匹配人數υ.

步驟3使用分層求解的方法確定最佳合乘匹配.

步驟4考慮到通勤合乘匹配模型首先要方便最多的通勤者出行，以式(1)作為第一目標函數.對于任意匹配z(i,J,(k,g))∈Z，將乘客組J內乘客z(i,J,(k,g))依據合乘模式做匹配.如在同性合乘模式下，依據式(10)～(11)，式(16)～(18)對J內乘客進行if-then約束，判斷乘客組J內乘客是否滿足同性合乘模式.

當乘客組J滿足性別合乘模式時，對乘客j∈J，將乘客j和可行匹配z(i,J,(k,g))對應的控制變量xjz賦值為1，即xjz=1.將司機i和可行匹配對應的控制變量xiz賦值為1，即xiz=1.其他的控制變量賦值為0.將所有控制變量(xjz和xiz)賦值之后，以式(3)～(9)、式(19)～(21)為約束條件，以式(1)為模型的目標函數對合乘匹配模型進行求解.模型求解后會得到模型中最多的通勤合乘參與人數.

步驟5為了使模型在限制最少合乘參與人數條件下實現合乘行駛距離最小化，利用步驟4結果構造如下新約束條件：

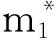
(22)

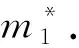
此時求解的模型目標函數為式(2)，約束條件增加式(22).在限制最少合乘參與人數條件下，求解新模型可得到整個通勤走廊中最大的機動車行駛距離優化值.

3 算例分析

算例路網見圖3.通勤走廊路網中共有22個節點.其中1～16節點為普通節點，17～22節點為合乘點.實線上數字表示兩點間的距離(單位km)，且路網節點之間可以相互直達.設定機動車行駛速度40 km/h，乘客步行速度為5 km/h.司機能接受的最大行程時間T直接設置為司機通勤最晚到達時間與最早出發時間的差值.時間消耗τ值為0.1 h.乘客的容忍系數?由MATLAB軟件rand函數隨機產生.機動車最大載客量統一設定為4人.

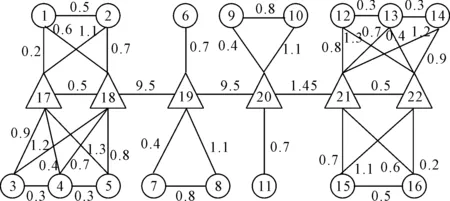
圖3 單通道合乘通勤走廊示意圖

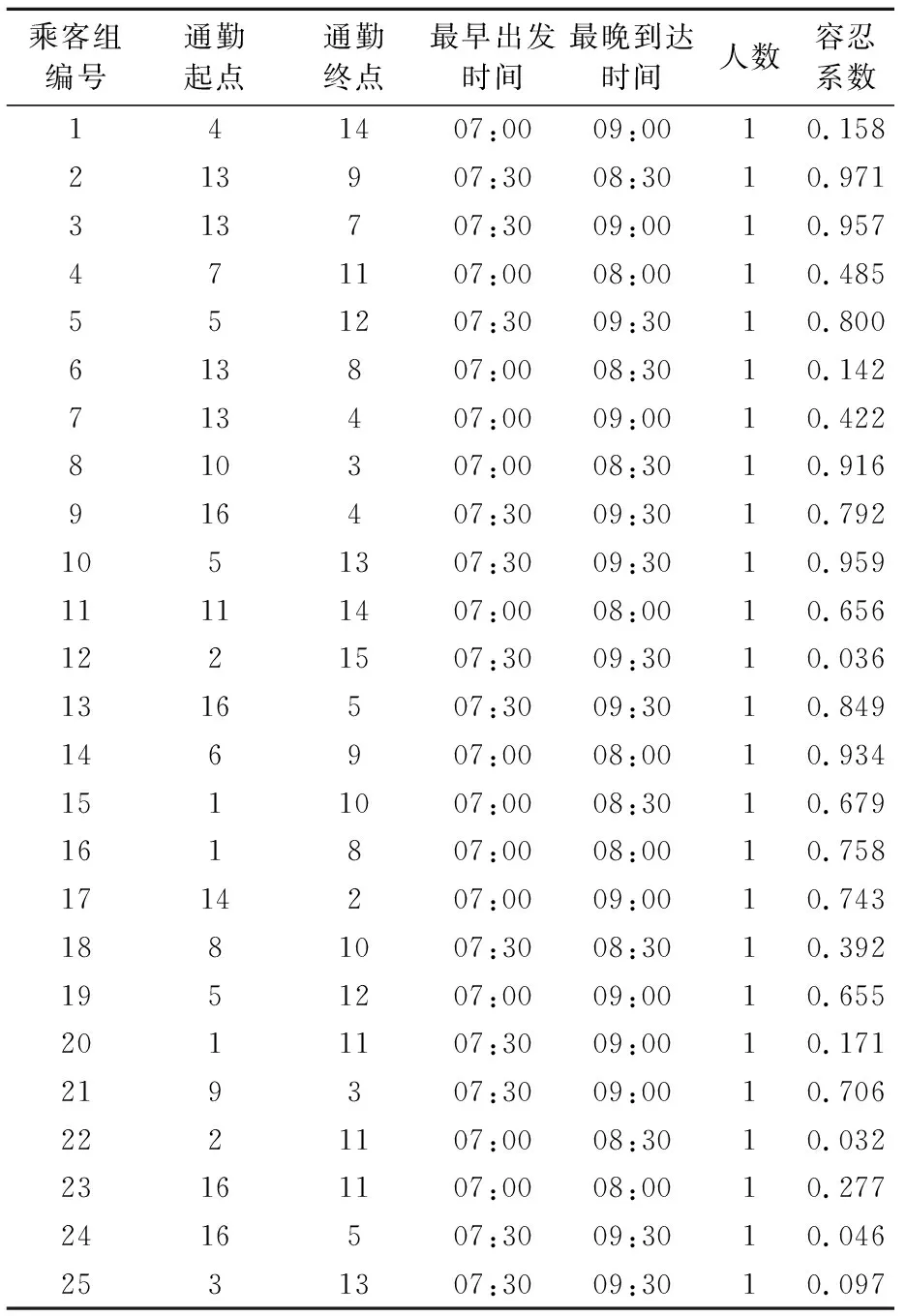
表1 部分乘客出行信息

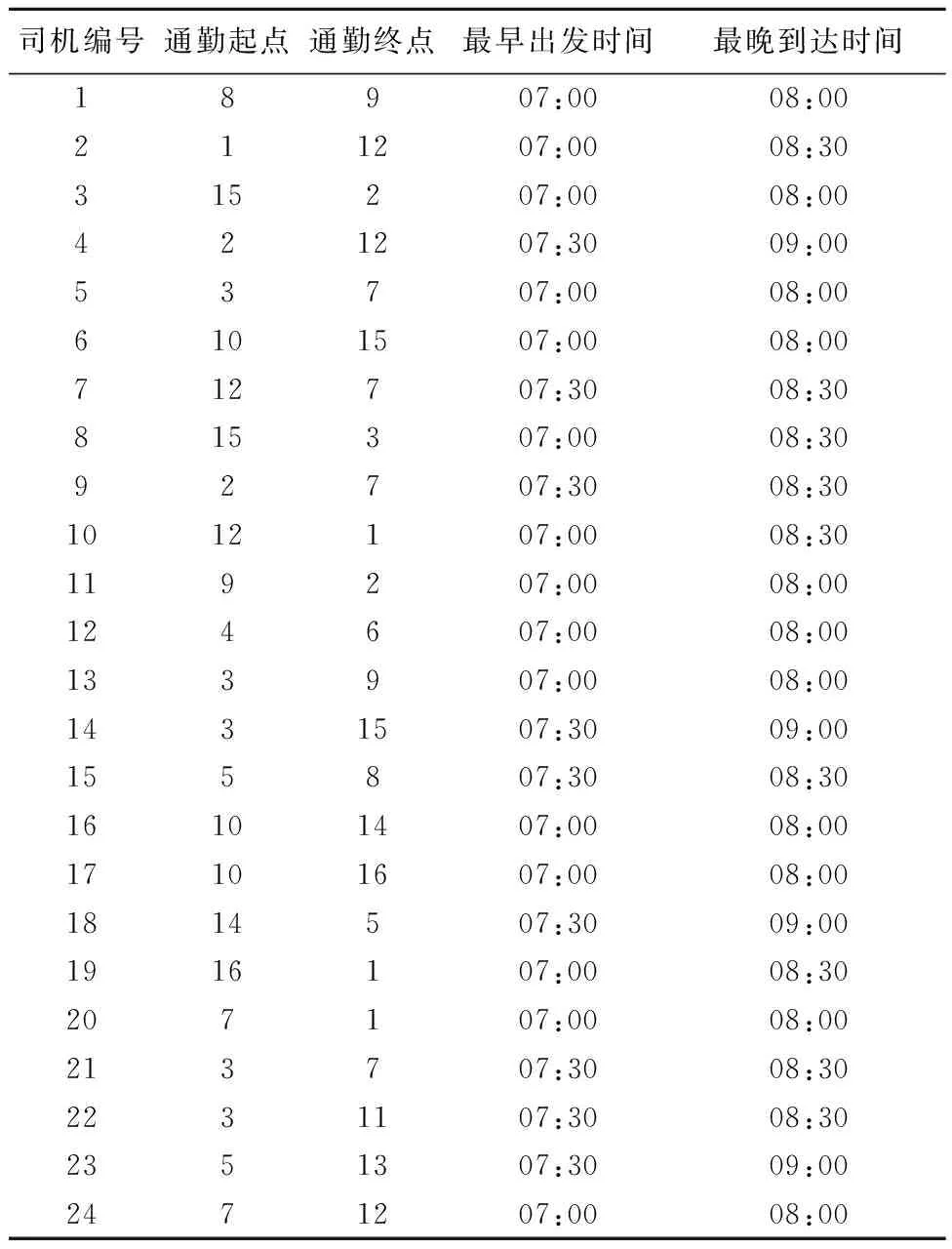
表2 部分司機出行信息

首先考慮第一種合乘模式，即模型約束在性別匹配約束時選擇式(10)～(11)加入模型計算.模型的運算部分使用軟件MATLAB進行編程運算.模型最終計算結果見圖4.

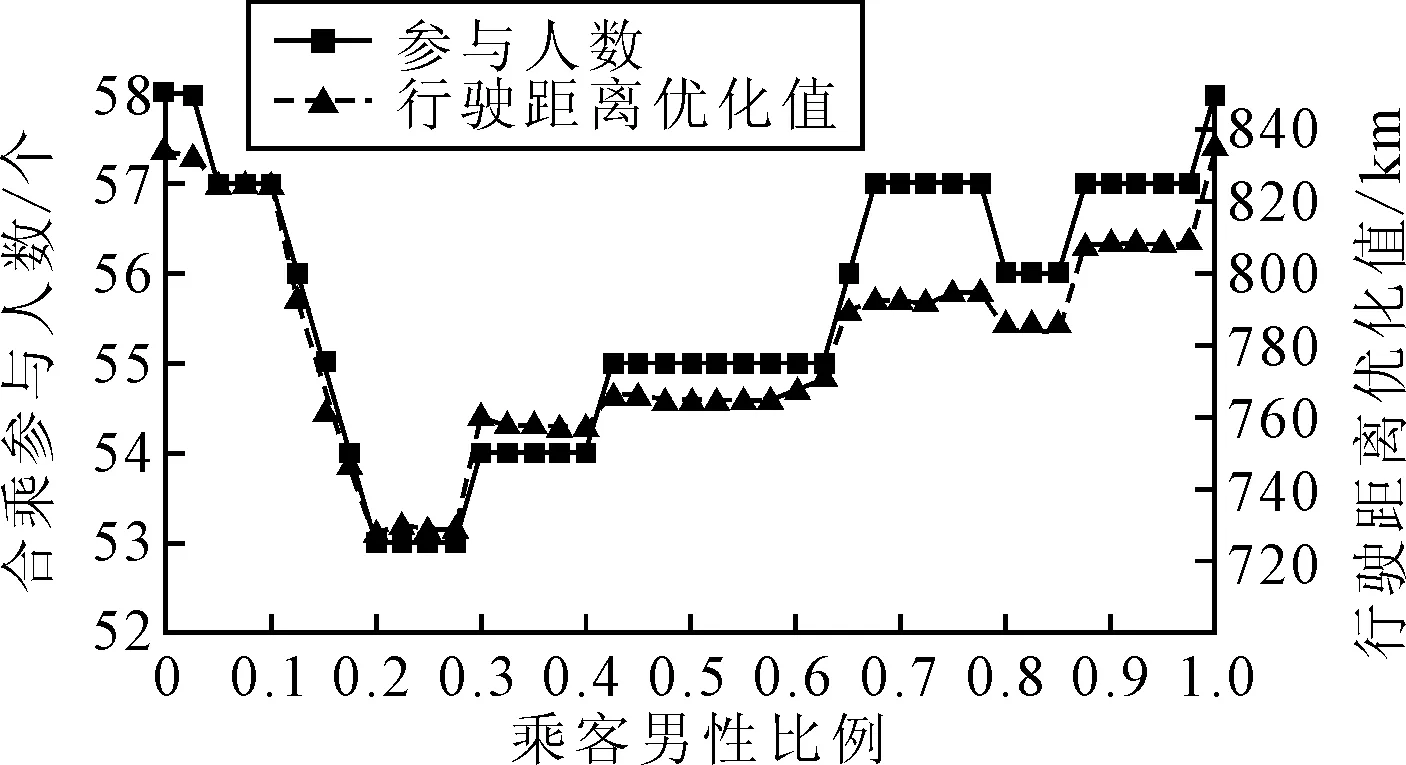
圖4 同性合乘模式結果統計圖

下面考慮第二種合乘模式，即模型約束在性別匹配約束時選擇式(12)～(13)加入模型計算.模型運算結果見圖5.

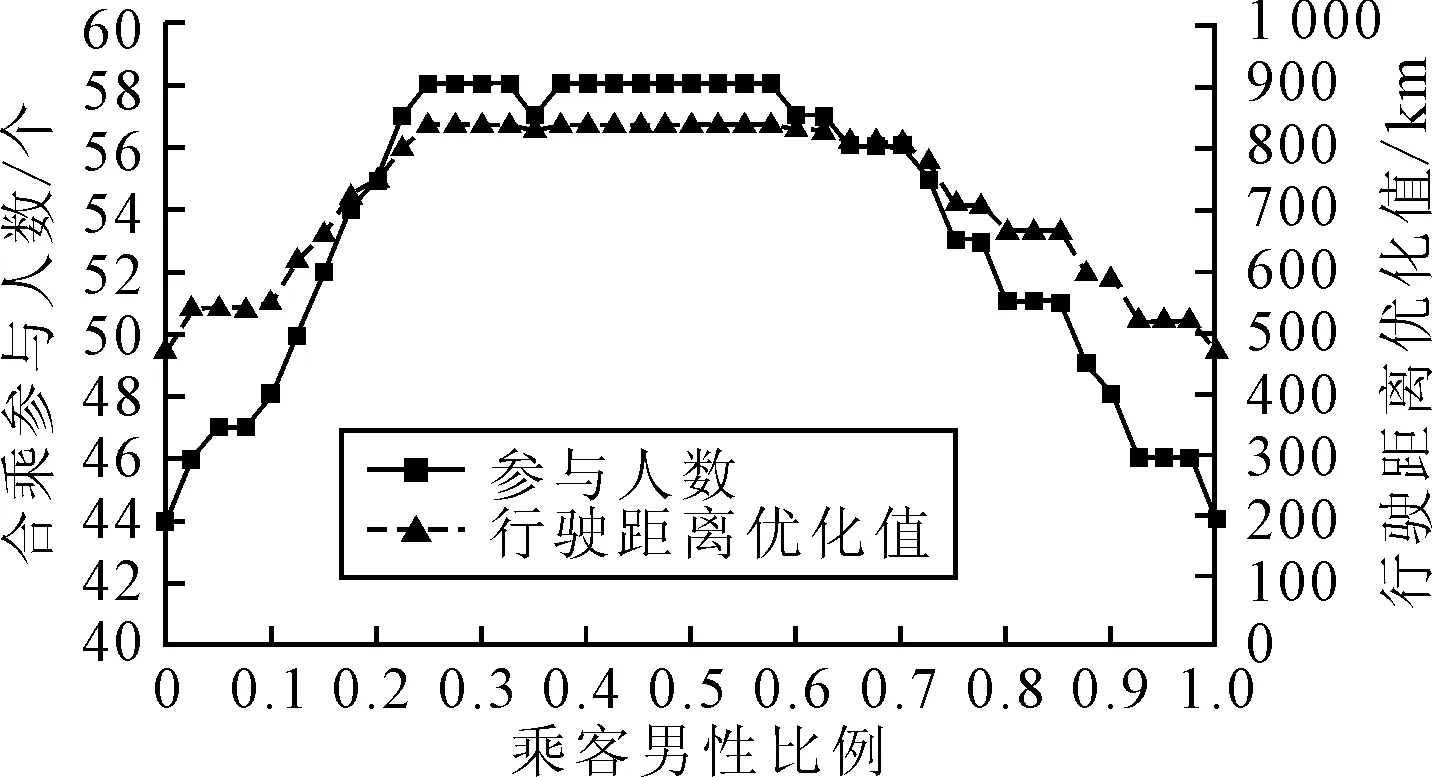
圖5 異性合乘模式結果統計圖

考慮第三種合乘模式中男性乘客和女性乘客皆偏好和女性乘客進行合乘組成通勤乘客組.即模型約束在性別匹配約束時選擇式(14)～(15)加入模型計算.模型運算結果見圖6.

圖6 特別組合合乘模式結果統計圖

從上面對三種性別合乘模式的運算結果可以得出如下結論.

1) 模型輸出數據中機動車行駛距離優化值σ與合乘人數υ成正相關.乘客男性比例變化時，圖4～6中行駛距離優化值和合乘參與人數的變化趨勢相同.因為合乘參與人數變多，說明參與的乘客增多.行駛距離優化值σz=doidi-(doik+dkg+dgdi)+∑j∈J(dojdj-(dojk+dgdj))，其中越多乘客參與通勤合乘，∑j∈J(dojdj-(dojk+dgdj))值會相應增大，σz值也相應增大.因為每位乘客帶來的優化值不同，所以行駛距離優化值σ與合乘人數υ呈現正相關趨勢，并不是嚴格正比例關系.

2) 模型輸出結果與預期結果相符，印證了包含性別屬性匹配模型的有效性.其中在同性合乘模式下，男性乘客或女性乘客占總乘客數比值越高，合乘匹配效果越好；在異性合乘模式下，某一性比乘客數占比越高，越不利于合乘匹配的進行；而在特別組合性別合乘模式下，被偏好性別乘客數越高，匹配效果越好.

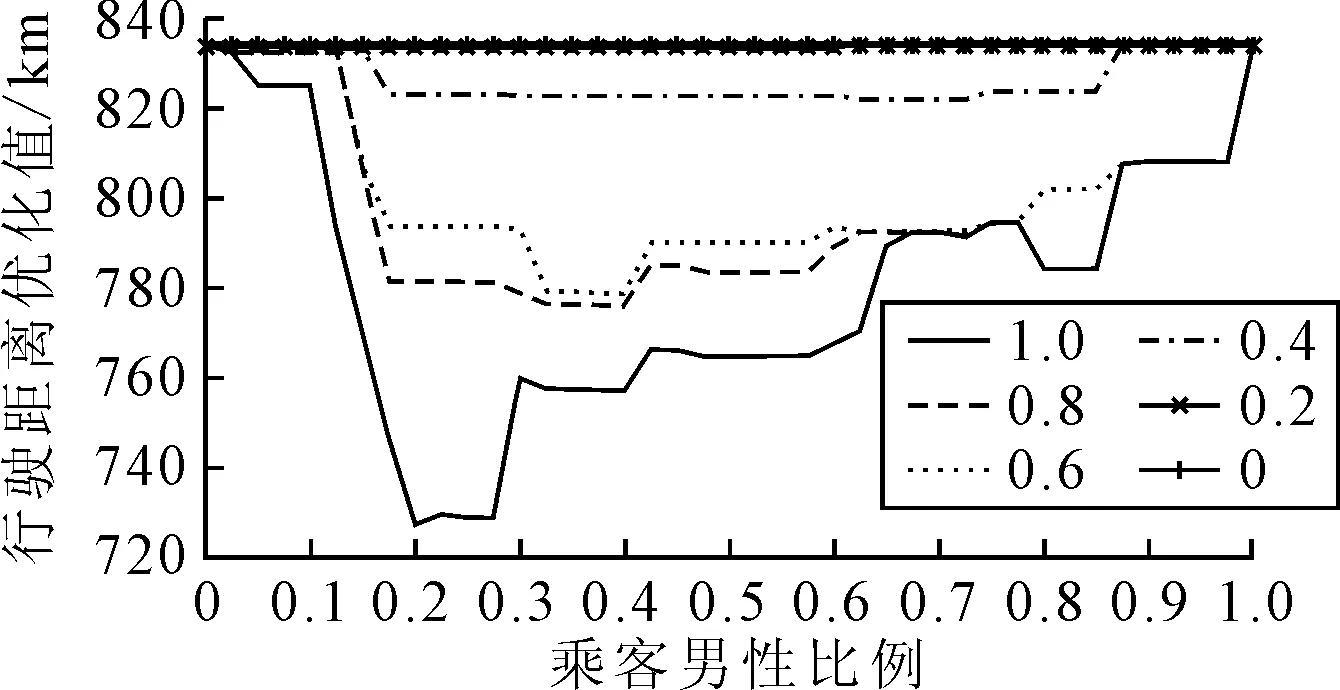
圖7 控制系數分析統計圖

4 結 束 語

針對城市交通中的通勤合乘安全問題，本文提出了一種考慮乘客性別影響的通勤車輛司乘匹配模型.模型中涵蓋同性合乘、異性合乘和組合合乘模式，并使用不同約束條件體現性別合乘模式對通勤乘客匹配的影響.算例分析在證實通勤車輛合乘匹配模型有效性的同時，還為現實處理合乘問題中提供以下的指導意見.通勤乘客對合乘同伴性別的偏好會對匹配產生一定影響，為了將負面影響效果降至最小，現實中可以將具有類似合乘偏好的乘客進行分組處理.例如將具有同性合乘偏好的乘客按照性別進行分組，以提高組內乘客某一性別占比；同樣對異性合乘偏好乘客進行分組，以均衡組內乘客性別占比，其中男女乘客比值為1∶1時司乘匹配效果為最佳.