基于過渡圓弧半徑求解方法的無人艇循跡控制研究*

韓 鑫 徐海祥 余文曌 周志杰

(高性能船舶技術教育部重點實驗室1) 武漢 430063) (武漢理工大學交通學院2) 武漢 430063) (欽州學院機械與船舶海洋工程學院3) 欽州 535099)

0 引 言

無人艇循跡控制是指無人艇在工作或航行過程中，沿著某一條預定的軌跡運動，此過程中要求保持無人艇的艏向沿著預定軌跡.國內外學者已對船舶循跡控制做了大量工作，國外學者Fossen等[1-6]對欠驅船舶的循跡控制做了詳細討論，國內學者聶兵等[7-10]也對循跡控制做了相關研究.

無人艇循跡模式由三部分組成：路徑規劃、引導系統和控制系統.在路徑規劃中，路徑是由許多路徑點組成，其中最典型的連接方式是采用直線和圓弧光滑連接.Fossen[11]在相鄰的直線段間加入圓弧過渡，解決了路徑的不連續問題，但在經過圓弧時并沒有經過中間路徑點.文獻[7-8]對鋪管船的循跡控制進行了研究，通過在每一個路徑點處定義一個回轉半徑，實現直線間的光滑過渡.文獻[10]對欠缺船舶循跡控制進行了研究，并通過改進直線和圓弧的路徑規劃，使船舶經過圓弧時同時經過中間路徑點.雖然上述國內外學者都對循跡過程中路徑規劃做了相關研究，但是迄今為止過渡圓弧的半徑值都是人為給定的某一固定值，并沒有給出確切的圓弧半徑求解方法.而在實際的無人艇循跡控制應用中，如圓弧半徑取值過小，會使無人艇舵的性能達不到回轉性能要求，造成實際路徑與規劃路徑不吻合；如圓弧半徑取值過大，則造成無人艇實際路徑與直線連接路徑產生較大的偏移.

針對圓弧半徑的取值問題，本文對圓弧半徑的求解問題進行了研究，提出一種圓弧半徑的求解方法.

1 無人艇定常回轉運動的受力分析

無人艇作定常回轉運動時，回轉樞心記做點P，見圖1.此時無人艇舵產生的轉舵力矩與無人艇受到的阻力矩平衡.

圖1 無人艇回轉樞心

無人艇在經過中間路徑點時需要圓弧過渡，對于主推帶舵推進系統的無人艇而言，需要在已知操縱性能的條件下，計算出滿舵條件下圓弧的最小曲率半徑.最后，通過安全系數來確定無人艇循跡過程中過渡圓弧的半徑.

針對無人艇循跡過程中圓弧半徑取值問題，本文考慮了環境阻力矩對無人艇回轉運動的影響，完善了文獻[11]提出的求解無人艇回轉半徑的方法，使其更加符合無人艇循跡控制的條件.

1.1 無人艇轉舵力矩

無人艇舵產生的轉舵力矩，可由經驗公式計算得出.

ρAu2l

(1)

式中:CL為舵的升力系數;ρ為水的密度;A為舵葉的一側浸水面積;l為舵桿軸線到無人艇重心的距離.

1.2 靜水阻力矩

無人艇在靜水中運動時，只需考慮水產生的阻力矩.無人艇作定常回轉運動時，繞樞心P勻速轉動(見圖2)，回轉運動過程中，水產生的阻力矩與無人艇的形狀與水下縱剖面積有關.假定水下中縱剖面為矩形，此矩形產生的阻力矩即無人艇在靜水中回轉運動所受的阻力矩.

圖2 無人艇中縱剖面

根據文獻[11]得出靜水對無人艇產生的阻力矩為

(2)

式中：ω為無人艇繞樞心轉動的角速度.

1.3 環境阻力矩

無人艇正常工作時，其運動會受到來自風、浪、流等環境載荷的影響，從而影響其回轉半徑大小.假定無人艇在回轉過程中受到的最大環境擾動力矩為bmax，則環境載荷產生的最大阻力矩為

(3)

1.4 曲率半徑

假定無人艇在過渡圓弧處做定常回轉運動，此時無人艇舵產生的力矩與靜水阻力矩和環境阻力矩相平衡，即

Nr+Ms+Me=0

(4)

將式(1)～(3)帶入式(4)得

(5)

則角速度ω為

(6)

無人艇作定常回轉時，如果其轉動角度π,則運動的距離為πR，兩者經過的時間相同，即

(7)

將式(6)帶入式(7)，考慮安全系數k2(k2>1，取k2=1.5)，得出

(8)

由式(8)可知，無人艇循跡經過中間路徑點的圓弧半徑R與無人艇及舵的一些基本參數和環境阻力矩有關，這些在仿真過程過程中都是作為已知參數輸入,因此，任意無人艇在循跡過程中的圓弧半徑R都是通過計算得出的已知量，避免R取值的人為性.

2 無人艇運動數學模型

無人艇在循跡過程中，一般只考慮三個自由度的影響，即縱蕩、橫蕩和艏搖.為了描述無人艇在三自由度的運動情況，建立北東坐標系OE-XEYEZE和船體坐標系O-XYZ，見圖3.其中，北東坐標系中原點取海上或陸上任意一點，XE軸指向正北，YE軸指向正東，ZE軸指向地心；船體坐標系中原點取水線面、中縱剖面和中橫剖面的交點，X軸指向船首為正，Y軸指向右舷為正，Z軸指向基線為正.

圖3 北東坐標系和船體坐標系

根據文獻[1]，無人艇三自由度的數學模型為

(9)

式中：M∈R3×3為慣性矩陣；C(ν)∈R3×3為科里奧利向心力矩陣；D(ν)∈R3×3為阻尼系數矩陣；τ∈R3×1為推進器推力；b∈R3×1為作用在無人艇上的環境擾動力；up=[Tp,δ]T為螺旋槳的推力和操舵角組成的向量；Bu∈R3×3為執行機構的配置矩陣；Tu為表征執行機構動態響應速率的定常矩陣；uc=[Tpc,δc]T為控制器的輸出；η=(x,y,ψ)T為無人艇在固定坐標系下的位置；ν=(u,υ,r)T為無人艇在船體坐標系下的速度；R(ψ)∈R3×3為坐標轉換矩陣.模型中矩陣的具體形式為

對于主推帶舵的無人艇，Bu和up為

式中：t為推力減額分數；Yδ和Nδ為舵的水動力系數.對于欠驅無人艇，控制器輸出up表示為

(10)

式中：umax和umin分別為無人艇推進器推力和舵角的最大值和最小值.

3 引導系統和控制器設計

引導系統設計中，本文引入路徑平行坐標系(path parallel)的概念，該坐標系的X軸與路徑相切，Y軸與X軸成右手坐標系，見圖4.

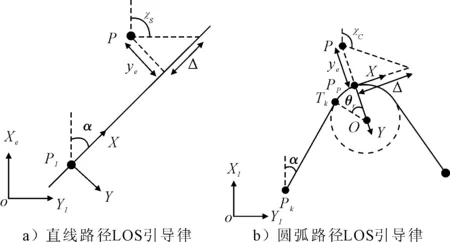
圖4 直線和圓弧的LOS引導律

對于直線路徑而言，無人艇循跡過程中所需要的艏向角ψd，即為圖4a)中所示的引導艏向角χs，χs表示為

(11)

對于圓弧路徑而言，無人艇循跡過程中所需要的艏向角ψd，即為圖4b)中所示的引導艏向角χc，χc表示為

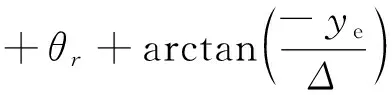
(12)

式中：Δ為時變的前向距離；ye為橫向偏差.

本文采用文獻[10]采用的反步積分控制器，其縱向和艏向控制率：

(13)

4 仿真結果及分析

為了驗證圓弧半徑求解方法在無人艇循跡過程中的合理性，采用挪威科技大學Cybership 2模型進行無人艇循跡控制仿真，其中模型參數、LOS引導律、控制器和環境力等參數見表1.

無人艇循跡過程中設定五個路徑點，坐標值見表2.

根據本文提出的圓弧半徑求解方法，得出仿真船模在所設環境條件下的圓弧半徑R≈1.2 m，為了驗證圓弧半徑求解方法的有效性，在控制器參數等條件都相同的前提下，設計兩種仿真情況的圓弧半徑.①三段圓弧半徑均為1.2 m；②三段圓弧的半徑分別為0.5，1.2，2 m.

采用line of sight (LOS) 引導律和基于反步積分和Lyapunov理論的非線性控制器對無人艇循跡控制進行仿真，仿真結果見圖5～7.

圖5為無人艇在兩種情況下均達到了循跡控制的效果，由圖5a)可知，無人艇在整個循跡過程中實際路徑與規劃路徑吻合的非常好，并且實際路徑與直線連接路徑也未發生較大偏移；圖5b)在圓弧半徑R=0.5 m處，無人艇的實際路徑與規劃路徑并不能很好的吻合，造成該結果是因為無人艇舵的性能不足，無法達到規劃路徑的回轉效果；在圓弧半徑R=2 m處，雖然無人艇的實際路徑與規劃路徑吻合的非常好，但是實際路徑與直線連接路徑發生較大的偏移，是因為圓弧半徑取值過大造成的.

表1 相關參數

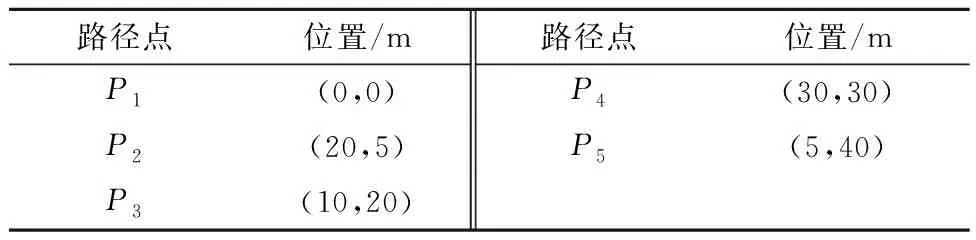
表2 路徑點設定值

圖5 無人艇運動軌跡圖

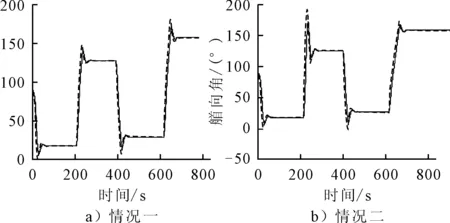
圖6 無人艇實際艏向角和LOS引導艏向角

圖6為實際艏向角和LOS引導艏向角的變化情況，兩者達到了非常好的吻合效果.但是通過比較圖6a)和b)對應的圓弧半徑R=1.2 m和0.5 m處艏向角的變化可知，圖6b)中半徑R=0.5 m時無人艇的實際艏向角和LOS引導艏向角的變化和變化率都較大，這對無人艇舵的性能提出非常高的要求.

圖7 螺旋槳推力和操舵角示意圖

圖7為螺旋槳的推力和操舵角變化情況，無人艇在兩種情況下運動時螺旋槳推力大小基本一致，但在圖7b)圓弧半徑R=0.5 m處，無人艇產生較大的操舵角和舵角變化率.這是因為圖6b)中在半徑R=0.5 m處艏向角的變化及變化率較大，使無人艇要產生較大的舵角和舵角變化率才能滿足其要求，如果其要求超出無人艇舵的性能所能達到的極限，將會導致圖5b)中在半徑R=0.5 m處實際路徑與規劃路徑不吻合的情況.

5 結 束 語

針對主推帶舵推進系統的無人艇循跡過程中過渡圓弧半徑的取值問題，本文對無人艇定常回轉運動時的受力情況進行了分析，提出了一種圓弧半徑的近似求解方法，并采用LOS引導系統及基于反步積分和Lyapunov理論的非線性控制器實現無人艇的循跡控制.最后，設計了兩組圓弧半徑，并分別在兩組圓弧半徑下對無人艇循跡控制進行了仿真運算，仿真結果表明了所提方法在無人艇循跡過程中的有效性.