渤海域橋梁斜體寬承臺冰荷載計算*

吳甜宇 邱文亮

(大連理工大學土木工程學院 大連 116024)

0 引 言

在寒區的海洋資源開發以及港口建設中，冰荷載是海上結構物的主要控制荷載[1].

海冰是渤海有別于我國其他海域的突出問題，是該海域嚴重的自然災害，對海洋結構的安全具有極大的威脅[2].渤海每年冬季都有海冰生成，它影響著渤海海上交通、漁業生產、油氣開發等海上事業的運營[3].

斜體結構作為一種廣泛應用于寒區海域的抗冰結構形式[4]，由于冰與斜體結構相互作用過程中能引起冰的彎曲破壞，相比其他破壞模式而言，可以有效的降低冰荷載的作用.加拿大聯邦大橋[5]在設計過程中將冰荷載作為控制荷載進行考慮，并采用錐體橋墩的抗冰措施來減小冰荷載的作用.經過多年實測，錐體的設置有效的降低了冰荷載的極值，且遠小于設計荷載.波斯尼亞灣的Kemi-I燈塔[6]也同樣在水面線處設置了斜體破冰結構；我國渤海JZ9-3與JZ20-2采油平臺[7]均采用窄錐結構作為有效的抗冰減災措施.為了對渤海域跨海橋梁斜體寬承臺進行冰荷載研究，本文針對四種規范中的計算方法開展渤海海域環境條件下不同參數對冰荷載的影響情況，采用作圖分析，對斜體結構上的冰荷載進行討論.

1 冰與斜體寬結構作用機理

斜體結構的優點在于冰體與結構相互作用過程中會引起冰體的彎曲破壞，顯然，相比冰體的擠壓破壞，結構承受的冰荷載要低得多.抗冰結構中斜坡角的設置可以明顯使結構所受的冰荷載減小，特別是對于相對薄的海冰.但是海冰在傾斜結構表面不斷攀升的過程中有可能導致結構表面設施的損壞，另外，還會增加結構的豎向荷載，這可能對惡劣土壤條件下的結構設計不利[8].

Croasdale[9]提出了一個冰與斜體結構相互作用的二維分析模型.盡管只是二維力學分析模型，但此模型對于寬體斜坡結構冰荷載的計算是合理的.然而，此模型卻不適用于窄體結構，它對于窄結構而言低估了冰體的破碎荷載.其原因在于海冰與窄坡面結構相互作用過程具有三維效應，海冰的破壞區域相比結構的寬度要大得多，不是所有破碎冰體都將在斜體面上進行爬升，一些冰體會自然的從結構表面清除，此時應該應用三維彎曲失效模型進行分析.

當冰體接近一個具有傾斜面的結構時，在第一次接觸時冰體開始在界面處發生彎折.隨著驅動力的增加，冰體繼續破壞，作用力增大.作用于結構表面的總冰力可以分解為豎向和橫向兩個分力，豎向分力使得冰體發生彎曲變形，當豎向分力增加到一定程度時，冰體將發生彎曲破壞.當冰體局部破壞后，斷裂的冰體會被臨近的冰體擠壓，開始沿結構斜坡面進行爬升，進而發生回轉跌落.由于需要額外的力來推動冰體攀升，這個過程中會產生更大的相互作用力，海冰與斜體結構相互作用的整個進程，見圖1.

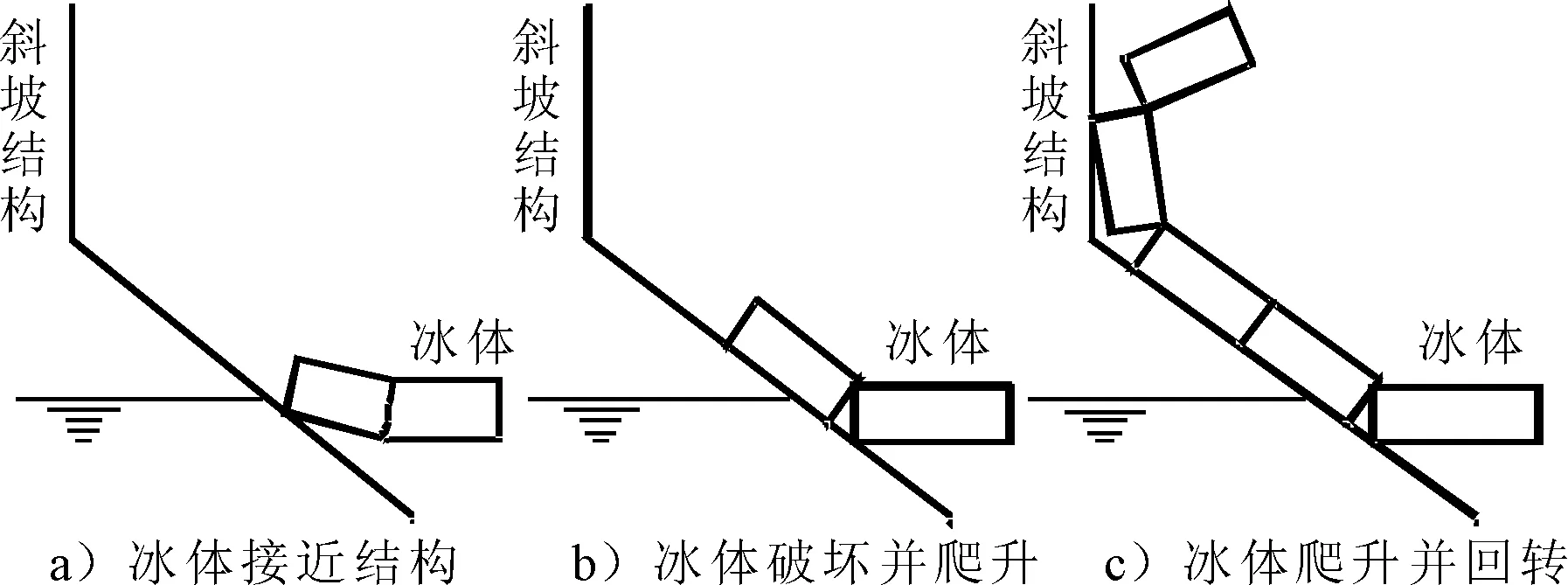
圖1 冰與斜體結構相互作用進程

另外，在冰與斜體結構相互作用的過程中，存在一些附加條件.當冰與斜體結構發生接觸后，斜體面結構需要具備有效的清理海冰的能力.若發生海冰附著于結構表面、海冰在結構面發生了堆積現象、或是結構被海冰包圍而無法清除，就會導致斜體面結構的所有優勢全部失效.在以上的情況之下，斜體面結構會表現出與直立面結構相同的破冰機理，見圖2.

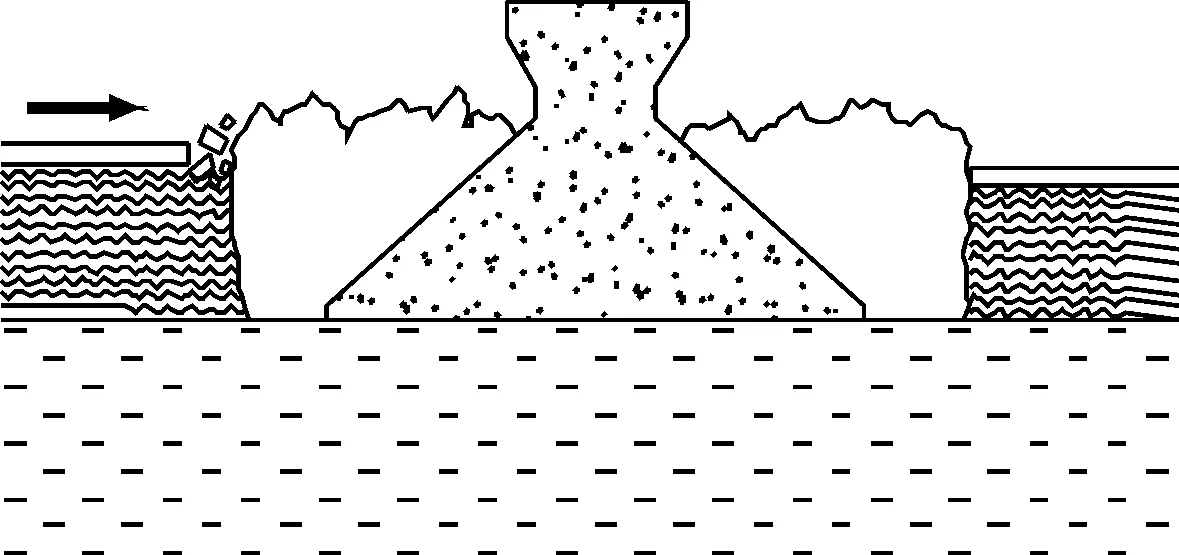
圖2 冰與斜體結構發生堵塞現象

文中主要討論平整冰與斜體寬結構的彎曲破壞力與爬升力，假定斜體的破冰效果良好，不會發生冰體堵塞現象.所以在此不針對冰體在斜體結構上的堆積作用進行深入探討.

2 各國規范斜體結構冰荷載計算方法

2.1 中國JTG D60規范

文獻[10]關于彎曲冰荷載的計算方法，規定當流冰范圍內有傾斜表面時，冰壓力應分解為橫向分力FH和豎向分力FV，斜體結構上的冰荷載推薦計算公式為

FH=m0Ctσfh2tanα

(1)

FV=FH/tanα

(2)

式中：m0為冰力系數，取0.2D/h，但不小于1；D為結構斜面寬度，m；Ct為冰溫系數；h為冰厚，m；σf為海冰彎曲強度，kPa；α為斜面與水平面夾角，(°).

2.2 中國Q/HSn規范

文獻[11]關于彎曲冰荷載的計算方法，規定冰與斜體海洋結構相互作用的橫向荷載FH與豎向荷載FV的推薦計算公式為

FH=Knh2σftanα

(3)

FV=Knh2σf

(4)

式中：Kn為冰力系數，取0.1D,D為結構斜面寬度，m；h為冰厚，m；σf為海冰彎曲強度，kPa；α為斜面與水平面夾角，(°).

2.3 俄羅斯SNIP規范

文獻[12]關于彎曲冰荷載的計算方法中規定冰與斜體結構相互作用的橫向荷載FH與豎向荷載FV的推薦計算公式為

FH=0.1σfDhtanα

(5)

FV=FHcotα=0.1σfDh

(6)

式中：D為結構斜面寬度，m；h為冰厚，m；σf為海冰彎曲強度，kPa；α為斜面與水平面夾角，(°).

2.4 加拿大CSA規范

文獻[13]對于斜體結構冰荷載的計算采用冰與斜體結構相互作用的二維力學分析模型，見圖3.

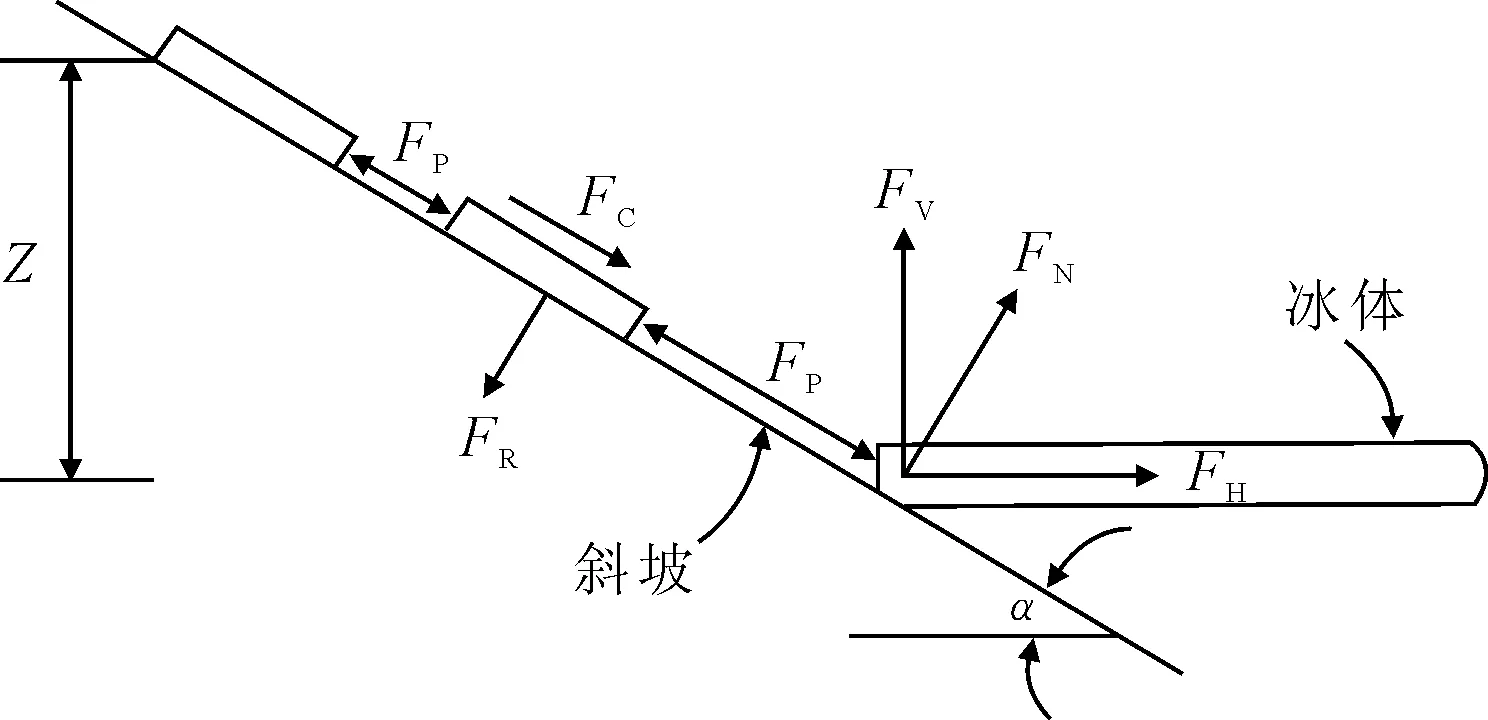
圖3 冰與斜體結構相互作用二維力學模型

冰與斜體結構相互作用力的橫向分量FH與豎向分量FV，可以寫為

FH=FNsinα+μFNcosα

(7)

FV=FNcosα-μFNsinα

(8)

FH=FVC

(9)

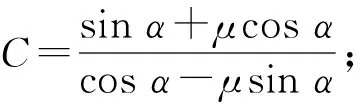
文獻[9]認為當冰體的彎曲強度與其初始彎曲破壞所需的豎向力相等時，那么結構單位寬度上的豎向力與橫向力，可以寫為

FV/D=0.68σf(ρwgh5/E)0.25

(10)

FH/D=0.68σf(ρwgh5/E)0.25C

(11)

式中:D為結構斜面寬度,m；h為冰厚，m；σf為海冰彎曲強度，kPa；ρwg為水的重力密度，N/m3；E為海冰的彈性模量，GPa.

Croasdale二維力學模型充分考慮了冰體在彎曲破壞后沿寬體斜坡的爬升作用，斷裂冰體在結構的斜面上還會被提升至一定的高度，隨后回轉跌落.冰體在斜面上被推升的垂直距離為Z，平行于斜體面的作用力FC可以寫為

ρig(sinα+μcosα)

(12)

式中：ρig為冰的重力密度，N/m3.

冰體彎曲破壞與爬升的橫向合力FH寫為

(13)

綜上，作用在斜體結構單位寬度上的水平總力可以寫為

FH/D=C1σf(ρwgh5/E)0.25+zhρigC2

(14)

式中：系數C1與C2只與斜面角度α與摩擦系數μ相關，可以寫為

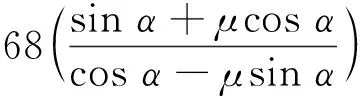
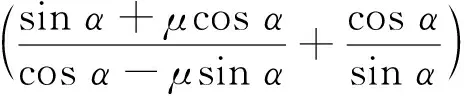
3 渤海域斜體結構冰荷載計算參數影響分析

參考文獻[11]，得到了渤海海冰的力學性能參數，并對結構計算參數進行了相關假定，見表1.

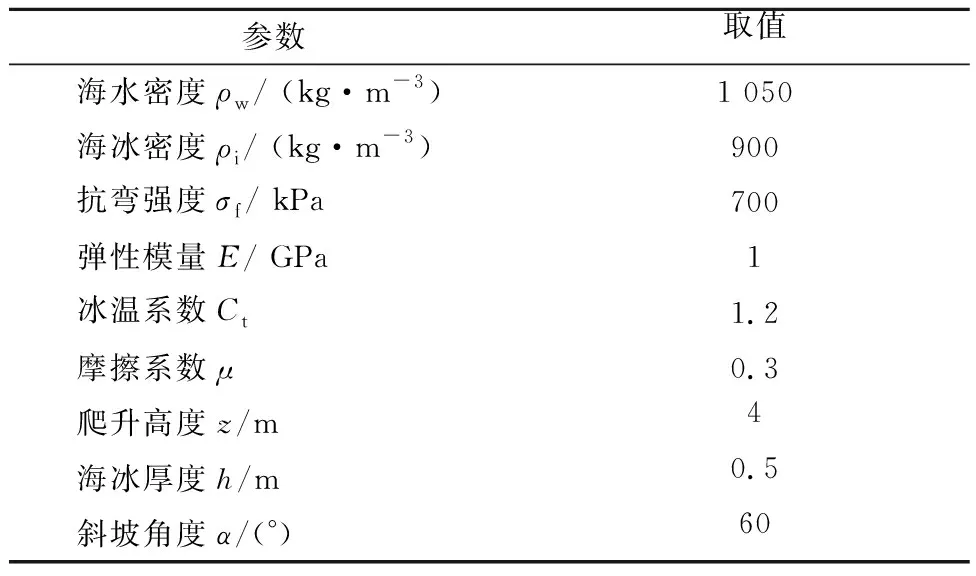
表1 計算參數

寒區結冰海域環境條件下，冰與斜體結構相互作用過程中，海冰對斜體結構起破壞作用的主要是冰荷載的橫向分力，所以在結構的抗冰設計過程中應當對橫向冰荷載進行重點關注.

圖4為各規范下結構的不同斜坡角度對橫向冰荷載的影響效應.由圖4可知，由于JTG D60，Q/HSn與SNIP規范均未考慮冰體沿斜體坡面的爬升作用，只給出了橫向與豎向的破壞荷載.然而，CSA規范給出了冰體爬升過程中任意高度處的橫向冰力，其中包括彎折力與爬升力兩部分組成.隨著結構斜坡角度的增大，橫向冰荷載均呈現增長的趨勢，但規范Q/HSn與規范SNIP計算所得的荷載水平較低.其中根據規范SNIP計算，斜坡角度由20°增大到65°，橫向冰荷載由13 kN/m增大到75.5 kN/m.規范JTG D60與規范CSA計算所得的冰荷載水平較高，且隨著斜坡角度的增加，橫向荷載的增長趨勢十分明顯.對于規范CSA而言，當斜坡角度大于45°時，橫向力對坡角的增大非常敏感，呈現了陡增的變化趨勢.橫向力也由20°坡角的47.9 kN/m增大到65°坡角的215.4 kN/m.可以觀察到，斜坡角度在30°～60°范圍內由規范JTG D60計算所得的橫向冰荷載要高于規范CSA的計算值，并遠大于其他兩個規范的計算值.由此可見，規范JTG D60在未考慮冰體爬升作用下的橫向荷載值偏大，側面說明了規范中給出的冰荷載的計算公式過于保守.

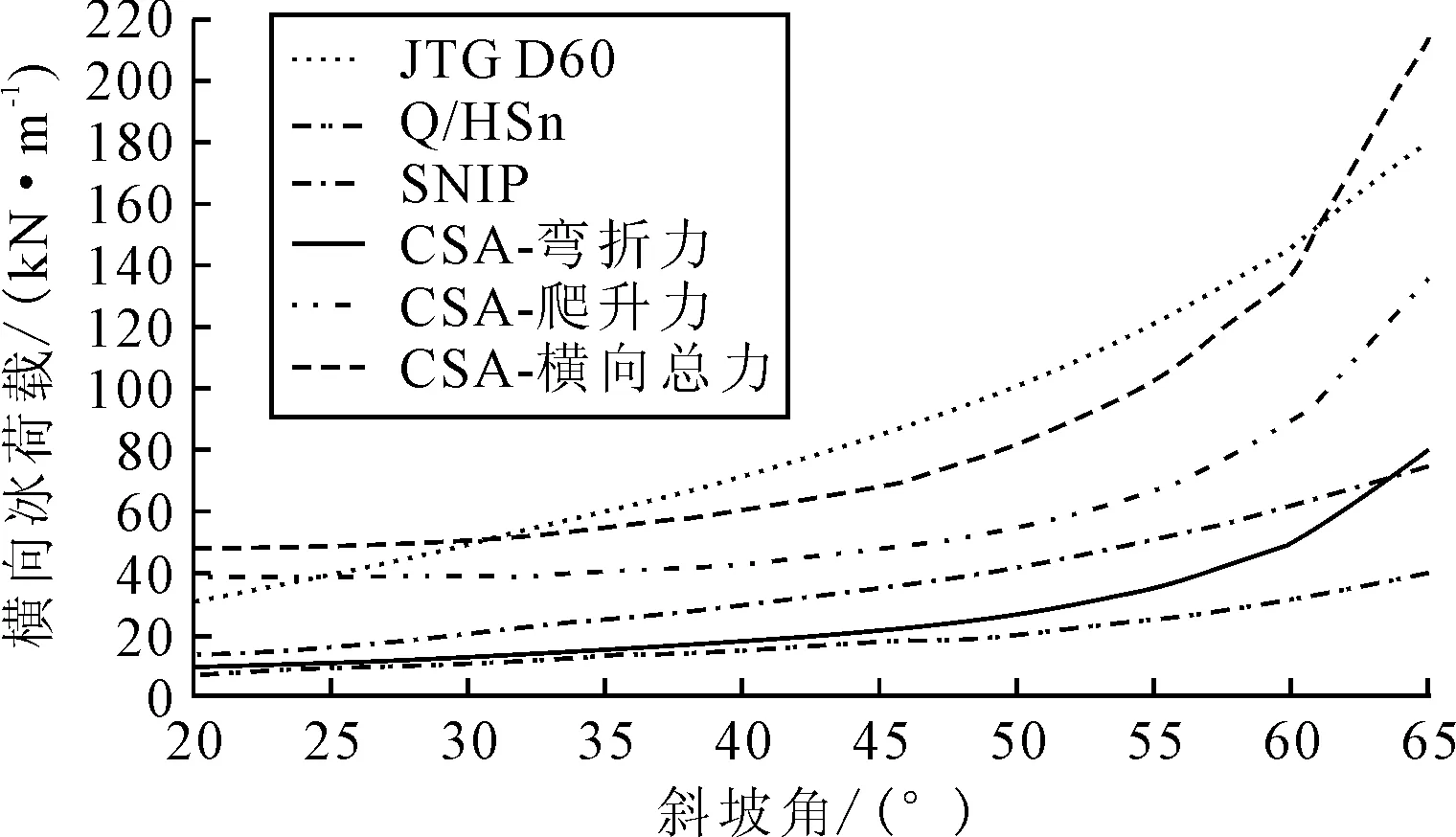
圖4 各規范下不同斜坡角橫向冰力

圖5為各規范下不同冰厚對橫向冰荷載的影響效應.由圖5可知，隨著冰厚的增加，各規范的計算冰荷載值均呈現增長的趨勢.在冰厚小于0.5 m下，根據規范Q/HSn計算得出的荷載值明顯低于其他規范的計算值.對于規范CSA計算的橫向總荷載而言，彎折力相對較小，爬升力占了主要的部分.對于寬結構的冰荷載計算，考慮爬升力的作用是合理、準確的.

圖5 各規范下不同冰厚橫向冰力

圖6為CSA規范下不同摩擦系數與不同爬升高度對橫向冰荷載的影響效應.由圖6a)可知，隨著斜坡角度的增大，橫向冰力呈現指數增長趨勢，冰與結構的摩擦系數越大，橫向冰力也隨之增大，即使在小坡角的情況下，荷載量值的變化也較為明顯.可見，在冰荷載的計算中，應當合理的選取冰與結構的摩擦系數.

由圖6b)可知，隨著冰厚的增大，橫向冰力呈現線性增長趨勢，冰體的爬升高度越大，橫向冰力也隨之增大.在冰厚為1 m的情況下，爬升高度由1 m增大到5 m，橫向冰力由138 kN/m增大到311 kN/m.

因此，在冰荷載的計算中，首先應當確定冰體在斜體結構上最大的爬升高度，準確合理的確定冰體爬升的最大高度是得到橫向冰荷載的前提條件.

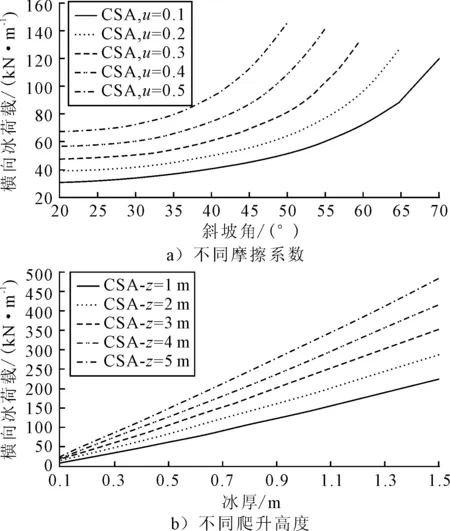
圖6 CSA規范下不同摩擦系數與不同爬升高度橫向冰力

4 渤海域橋梁斜體寬承臺冰荷載計算

擬建的“秦—大”跨海通道工程跨越渤海，連接遼寧省大連市與河北省秦皇島市，跨海部分均采用橋梁工程，海上工程長約144 km.由于橋址所在海域多為20～30 m的深水區域，故采用高樁承臺群樁基礎結構形式.非通航孔橋梁的典型承臺平面尺寸為21 m×13 m，考慮到本海域橋梁冰荷載問題，設計水面線位于承臺中部，承臺采用斜坡面的迎冰形式.

利用規范CSA進行橋梁承臺的冰荷載計算，選取海冰的爬升高度為5 m，海冰彎曲強度為700 kPa，冰與結構的摩擦系數為0.3，在四種斜坡角度，1 m冰厚范圍內，計算承臺冰荷載并繪制出承臺單位寬度橫向冰荷載曲線，見圖7.

圖7 CSA規范下不同斜坡角橫向冰力

由圖7可知，斜體面寬承臺結構與冰體相互作用的進程中，冰體所需的彎曲折斷力明顯小于冰體在斜體面上攀升所需的爬升力.針對假定的爬升最大高度5 m而言，各斜體設置角度下冰體所需的折斷力近似為爬升力的1/3，說明斜體面寬結構與冰體作用過程中爬升力相比折斷力占據主導地位.

對比圖7中的a)～d)可知，不同斜體設置角度下橫向冰荷載均隨著冰厚的增加而增大，且增長趨勢基本相似.當冰厚為0.5 m時，斜坡角為45°，50°，55°，60°的橋梁承臺(迎冰面21 m)橫向冰荷載分別為1 659，1 932，2 394，3 192 kN.

綜上，在進行橋梁斜體寬承臺的抗冰設計過程中，應當充分考慮設置角度、摩擦系數等結構因素的影響，應當合理的考慮施工難度、工程造價及結構合理性等綜合因素.

5 結 論

1) 對于寬結構而言，利用二維力學分析模型考慮冰體的爬升作用是合理、準確的.但對于窄結構而言，冰的清理機制或許取代了冰體的攀升作用，利用冰體的爬升公式計算的荷載值是偏高的，此時應采用三維模型進行計算.

2) 隨著冰厚、斜坡角度的增大，橫向冰荷載均呈現增長的趨勢.由于只考慮了冰體的彎曲破壞力，根據規范Q/HSn與規范SNIP計算所得的冰荷載水平略低.

3) 規范CSA利用二維力學分析模型，充分考慮了冰體在結構表面的爬升作用，計算所得的荷載值也明顯高于規范Q/HSn與規范SNIP，但規范JTG D60在未考慮冰體爬升作用的情況下荷載值偏大，說明其計算公式過于保守.

4) 橋梁斜體寬承臺的抗冰設計過程中，應當充分考慮斜坡面設置角度、摩擦系數等結構因素的影響，合理降低極值冰荷載，綜合考慮施工難度、工程造價等因素.