地鐵隧道考慮流固耦合影響的微裂隙巖體注漿數值模擬研究

倪向陽， 徐 程， 李偉平

(1. 青島地鐵集團有限公司， 山東 青島 266000； 2. 山東大學巖土與結構工程研究中心， 山東 濟南 250061)

0 引言

地鐵隧道施工過程中經常穿越微風化巖石地層，微風化巖石地層中一般發育開度較小(0.1～0.3 mm)的微裂隙。在地下水豐富的地區，微裂隙作為導水通道會溝通地下水與隧道臨空面，造成隧道滲漏水。目前，注漿是治理微裂隙巖體滲漏水的最常用手段。

裂隙巖體注漿過程是裂隙巖體變形與漿液擴散過程的耦合過程，尤其在微裂隙巖體注漿工程中，注漿壓力相比正常裂隙巖體注漿壓力更高，流固耦合效應更為顯著。漿液在注漿壓力的作用下進入巖體微裂隙中，漿液壓力作為外荷載作用于裂隙巖體，裂隙兩側巖體發生變形，進而影響整個巖體的受力變形狀態，裂隙開度逐漸增大。逐漸增大的裂隙開度會導致裂隙滲透性能發生改變，進而影響漿液流場。

關于裂隙注漿理論，國內外學者進行了廣泛的研究。文獻[1]建立了基于漿液黏度時變性的巖體裂隙注漿擴散模型； 文獻[2-5]推導了C-S漿液在單一平板裂隙中的壓力分布方程； 文獻[6-12]提出了相對擴散距離與相對擴散時間的概念，并用于描述裂隙注漿過程； 文獻[13]研究了漿液壓力與裂隙變形之間的關系，引入了裂隙張開臨界壓力的概念； 文獻[14]研究了裂隙巖體注漿過程中裂隙張開變形機制，并討論了裂隙張開變形對注漿效果的影響； 文獻[15]通過有限元方法獲得了相應的裂隙開度變化規律。以上研究均側重于裂隙內部的漿液流動過程，并假定裂隙開度在注漿過程中保持不變，與實際情況存在明顯差異。

本文著重考慮微裂隙巖體注漿過程中的流固耦合效應，進行有限元建模及計算分析，獲得考慮流固耦合效應的微裂隙巖體注漿擴散過程計算方法，研究裂隙開度及巖體彈性模量對注漿擴散過程的影響。對于微風化地層隧道中出現的滲漏水問題，基于本文所提出的計算方法能夠計算漿液的擴散距離以及圍巖的變形量，為實現滲漏水安全有效的控制提供了新的思路。

1 流固耦合理論

1.1 基本假設

1)巖體微裂隙簡化為平板裂隙，實際裂隙內部為不平整接觸面，裂隙粗糙度對滲透性能的影響轉化為裂隙滲透率對漿液擴散過程的影響。

2)裂隙兩側巖體視為各向同性、均質的完全彈性體，裂隙上下表面滿足無滑移邊界條件，裂隙表面處漿液流動速度為0。

3)漿液和水均為均質、各向同性的流體，漿液為牛頓流體，且注漿過程中漿液流型不變。

4)漿液擴散方式為完全驅替擴散，不考慮漿水相界面處水對漿液的稀釋作用。

5)不考慮漿液滲透到裂隙兩側巖體，漿液只在裂隙中擴散。

1.2 控制方程

地下水在隧道圍巖中的滲流運動通過達西定律描述，巖土體的應力與變形通過經典彈性力學理論描述。根據有效應力原理，水壓力與巖土體骨架有效應力之和為巖土體總應力。

漿液在裂隙內部的流動采用裂隙流理論描述，控制方程如下。

滲流連續性方程為：

。

(1)

裂隙流動立方達西定律運動方程為：

。

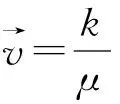
(2)

考慮流體的壓縮性，流體狀態方程為：

ρ=βρ0e-βp

。

(3)

根據彈性力學理論，巖土體受力變形服從平衡方程、幾何協調方程及本構方程。

巖體力學平衡方程為：

σji,j+Fi=0

。

(4)

幾何協調方程為：

本構方程為：

式(4)—(7)中：σ為巖土體應力，Pa；F為巖土體附加應力，Pa；ε為巖土體應變；E為彈性模量，Pa；u為巖體位移，m；δ為克羅內克符號;υ為泊松比。

漿液流動過程中通過裂隙表面向巖體傳遞漿液壓力，在裂隙表面處，漿液壓力與巖體應力相等，漿液流動與圍巖變形之間相互影響的理論紐帶即為裂隙表面處的壓力相等條件，如式(8)所示。

p界面,圍巖=p界面,流體

。

(8)

式中：p界面,圍巖為界面處圍巖應力；p界面,流體為界面處流體壓力。

2 有限元數值模型創建

采用Comsol Multiphysics創建數值模型，該軟件是以有限元法為基礎，通過求解偏微分方程(單場)或偏微分方程組(多場)來實現多物理場仿真計算。計算模型由裂隙與圍巖體構成，如圖1所示。裂隙采用單一水平裂隙，裂隙上下為圍巖體。

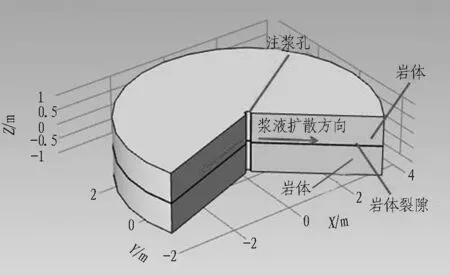
圖1 裂隙注漿計算模型

計算模型依托青島地鐵2號線東—環區間花崗巖微裂隙注漿堵水工程，根據現場對微裂隙花崗巖的裂隙統計，花崗巖裂隙開度為0.1～0.3 mm。本文裂隙開度計算參數取0.1 mm及0.3 mm 2種工況，通過鉆孔取芯測得花崗巖彈性模量為30～50 GPa。為研究不同圍巖彈性模量條件下流固耦合效應對注漿擴散過程的影響，花崗巖彈性模量取30 GPa和50 GPa 2種工況，花崗巖泊松比取0.3。注漿材料選用mw/mc=1∶1水泥單液漿，該種漿液黏度為10 MPa·s，注漿孔半徑取0.02 m，注漿流量取3 L/min。模型計算參數如表1所示。

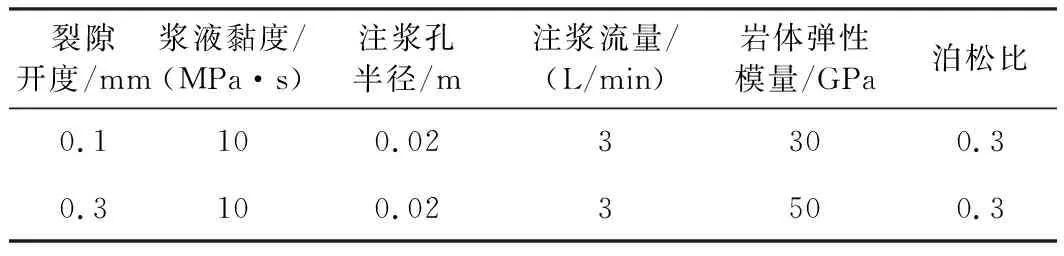
表1 模型計算參數

模型網格剖分及邊界條件如圖2所示。計算模型由3部分構成，模型中間為裂隙，裂隙上下均為巖體，裂隙單側巖體厚度為1 m，半徑為4 m。模型上下邊界均為固定邊界，不發生任何移動。模型側邊界為輥支撐邊界，只能發生豎直方向的位移，不能發生水平滑動。裂隙邊界為自由變形邊界，在漿液壓力作用下會發生被動變形，漿液由注漿孔位置進入裂隙。模型網格采用細化自由4面體網格，最小單元尺寸為0.02 cm，最大單元尺寸為4 cm，曲率解析度為0.25。為提高計算精度，在裂隙附近采用加密網格。

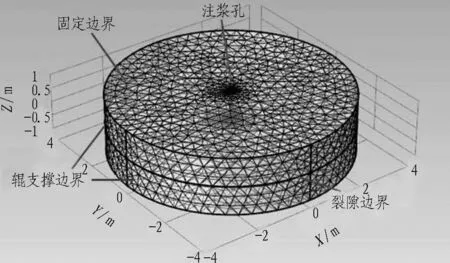
圖2 模型網格剖分及邊界條件

為研究注漿擴散動態過程，采用流體力學模塊與固體力學模塊進行多物理場瞬態計算。

3 微裂隙巖體注漿擴散規律分析

從漿液擴散壓力場、圍巖受力變形、裂隙開度時空分布、注漿壓力與注漿時間以及漿液擴散半徑的關系等方面對注漿擴散過程進行分析研究。

3.1 壓力場時空分布規律

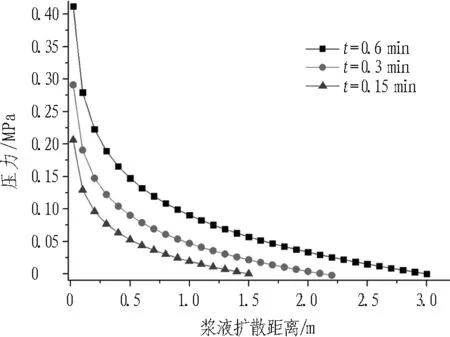
注漿過程中壓力場時空分布對比如圖3所示。

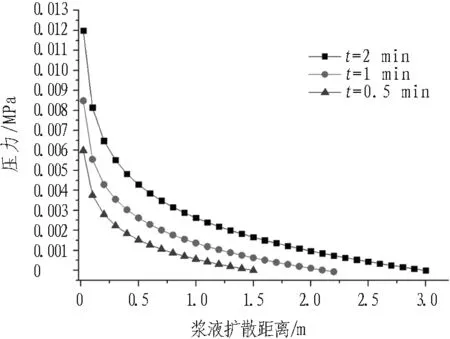
(a) E=30 GPa, b=0.3 mm

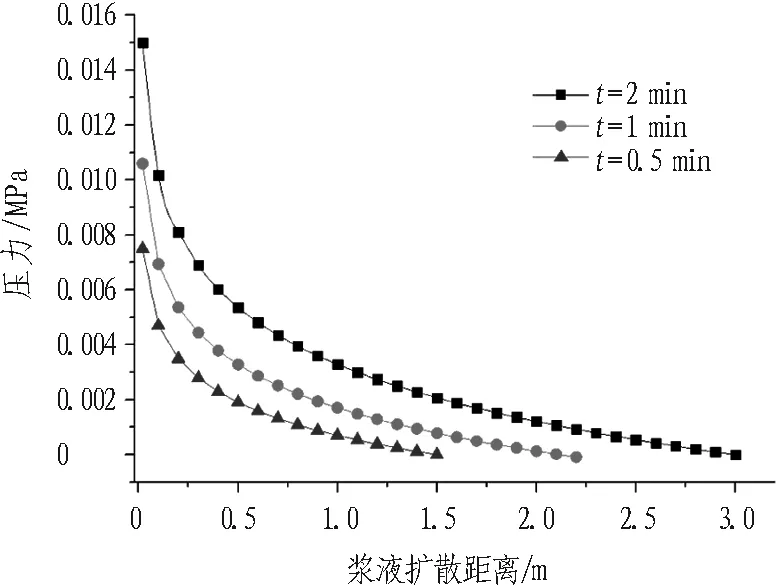
(b) E=50 GPa, b=0.3 mm

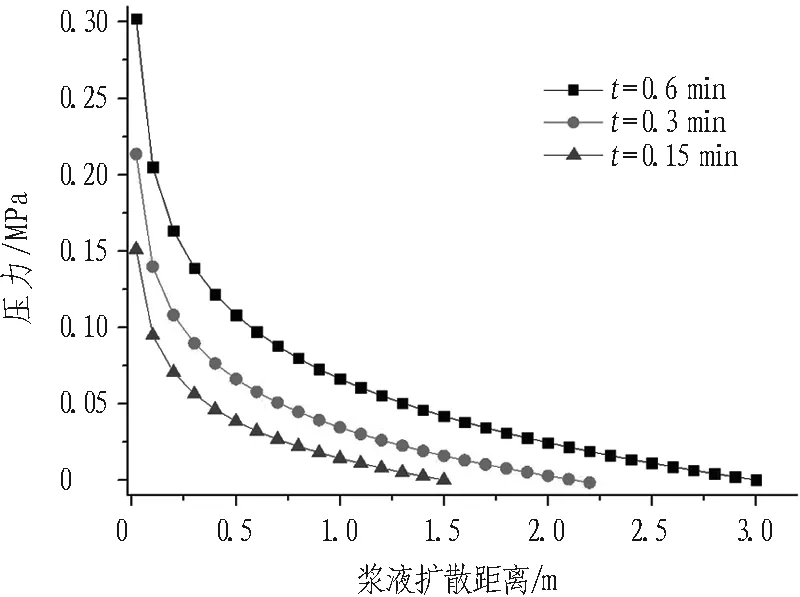
(c) E=30 GPa, b=0.1 mm

(d) E=50 GPa, b=0.1 mm

Fig. 3 Relationships between stress filed and grouting diffusion distance

由圖3可知：

1)同一時刻，漿液壓力沿擴散方向衰減，衰減速率隨擴散距離減小。

2)同一位置處，漿液壓力隨時間推移而升高。由于漿液擴散范圍的增加，進一步擴散所受到的阻力增大。

3)相同巖體彈性模量，裂隙開度越大，同一時刻、同一位置處，漿液壓力越小，漿液擴散距離越大。

4)相同裂隙開度，巖體彈性模量越小，漿液壓力越小。推斷是由于彈性模量越小，相同漿液壓力作用下，裂隙開度增加越大，漿液耦合效應越明顯的原因。

3.2 圍巖受力變形規律

E=30 GPa、b=0.1 mm時圍巖受力云圖如圖4所示。

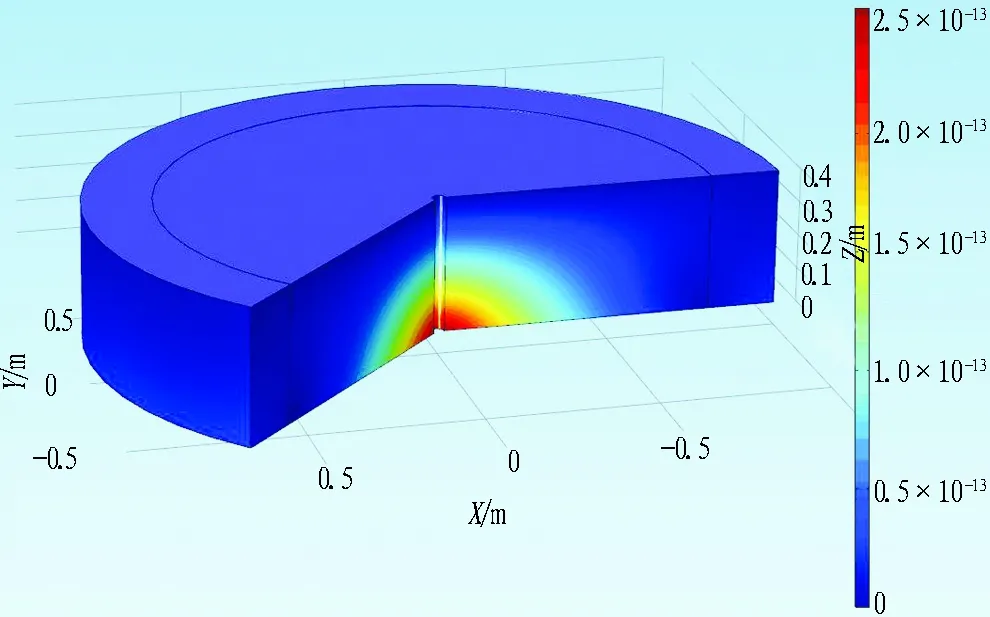
圖4 圍巖受力云圖(單位： GPa)

由圖4可知：

1)由于漿液壓力沿擴散半徑衰減，相應的作用于圍巖體的壓力也沿著擴散半徑衰減，注漿孔附近圍巖應力相對集中； 隨著漿液擴散距離的增大，圍巖所受應力逐漸減小。

2)由于注漿孔附近應力較為集中，當注漿壓力超過圍巖可承受的安全注漿壓力時，注漿孔附近區域最先發生塑性破壞。

3.3 裂隙開度時空變化規律

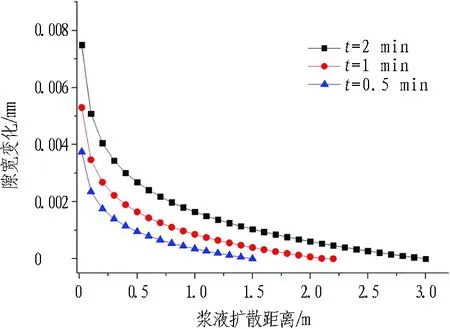
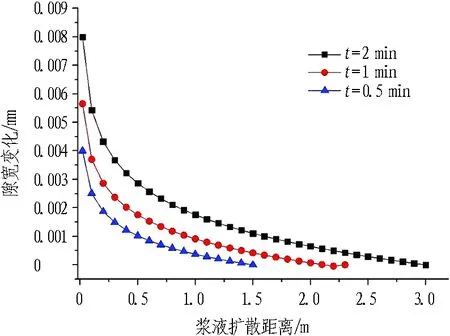
不同工況條件下，裂隙開度時空變化如圖5所示。

由圖5可知：

1)裂隙開度由注漿孔附近向漿液擴散鋒面處衰減，這與漿液壓力的空間衰減相對應，注漿孔附近的漿液壓力較高，對應的裂隙開度變化量大，最終獲得的裂隙開度也較大。

2)裂隙開度空間衰減速率隨著距注漿孔距離的增大而增大，這與注漿孔附近應力的快速衰減相對應。

3)不同彈性模量對應的裂隙開度稍有差別，當巖體彈性模量較大時，巖體不容易發生變形，導致漿液擴散阻力增加，同一位置處的漿液壓力隨之增大，但是由于巖體變形量較小，漿液壓力增大所應該引起的裂隙開度增加被巖體彈性模量增加所帶來的變形減小相互抵消，最終導致不同彈性模量巖體所對應的裂隙開度有差別，但差別不大。

(a) E=30 GPa, b=0.3 mm

(b) E=50 GPa, b=0.3 mm

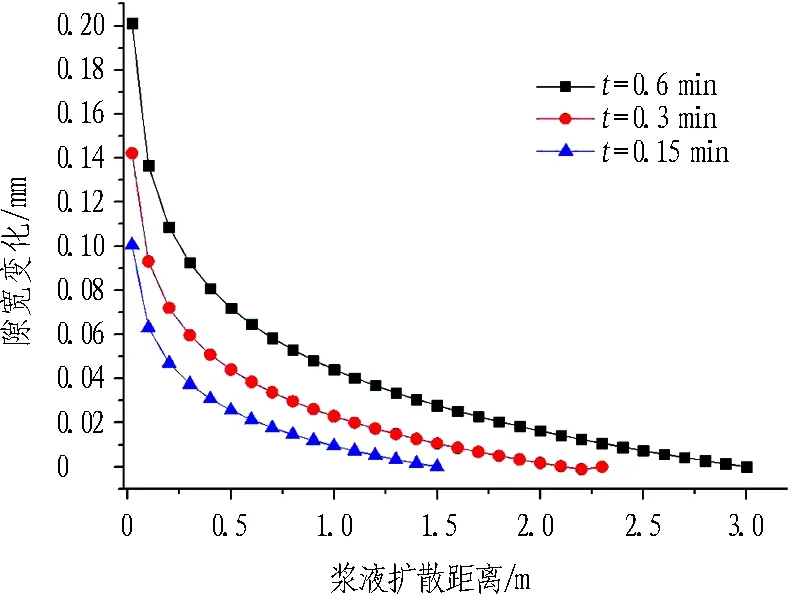
(c) E=30 GPa, b=0.1 mm

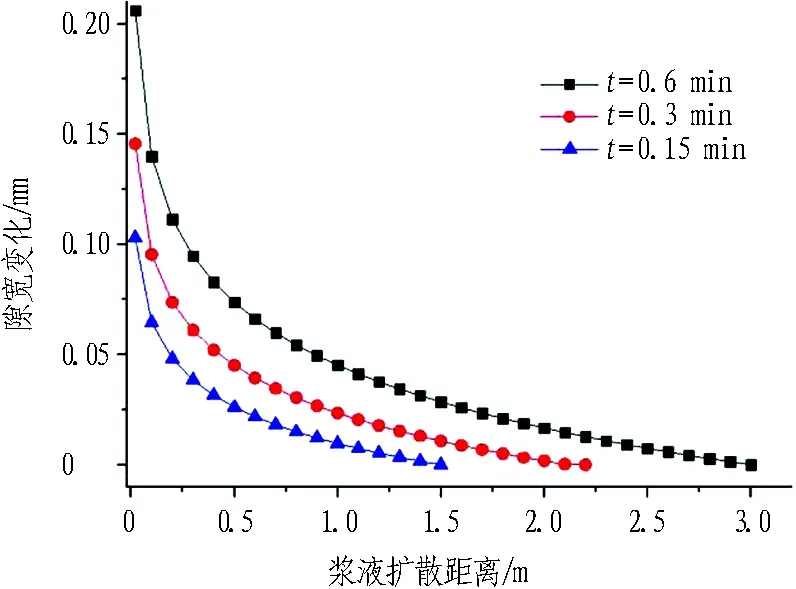
(d) E=50 GPa, b=0.1 mm

Fig. 5 Relationships between fracture opening and grouting diffusion distance

3.4 注漿壓力增長規律

不同工況條件下，注漿壓力隨時間變化規律如圖6所示。

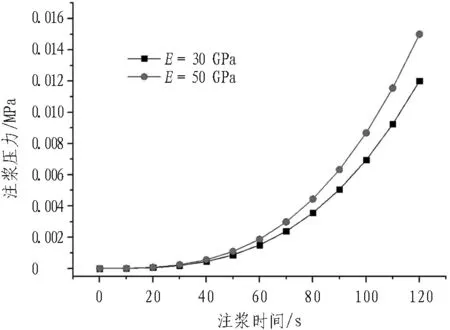
(a) b=0.3 mm

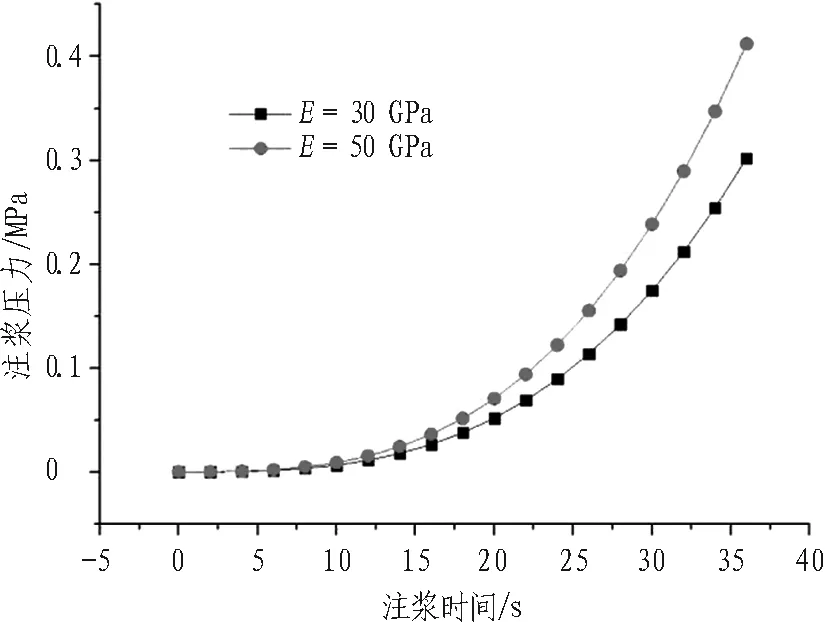
(b) b=0.1 mm

由圖6可知：

1)隨著注漿時間的增加，注漿壓力相應增大，注漿前期注漿壓力增長速率較慢，注漿后期注漿壓力增長速率加快。

2)當裂隙兩側圍巖彈性模量較大時，注漿壓力相應較高，這是因為圍巖彈性模量較高時圍巖難以壓縮變形，裂隙開度變化不大，故在該條件下對漿液擴散的阻力較大，最終導致注漿壓力較高。

4 考慮流固耦合效應的必要性分析

由于流固耦合效應的影響，巖體裂隙由于承受漿液壓力而導致裂隙隙寬變大，裂隙滲透率增大，進而導致裂隙巖體本身所引起的漿液擴散阻力減小。以往裂隙巖體注漿擴散理論較少考慮流固耦合效應對注漿擴散過程的影響，導致注漿壓力、注漿擴散范圍與實際測量值有較大區別，本節通過考慮與不考慮流固耦合效應時注漿壓力與漿液擴散范圍的對比，分析考慮流固耦合效應的必要性。

4.1 注漿壓力方面

考慮與不考慮流固耦合效應2種情況下注漿壓力對比如圖7所示。

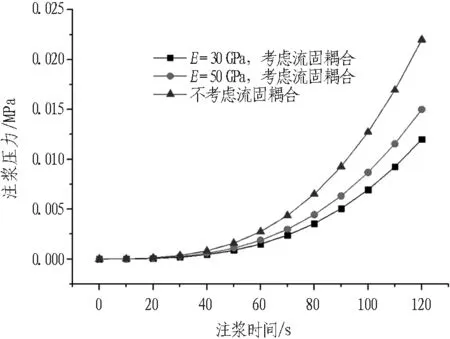
(a) b=0.3 mm

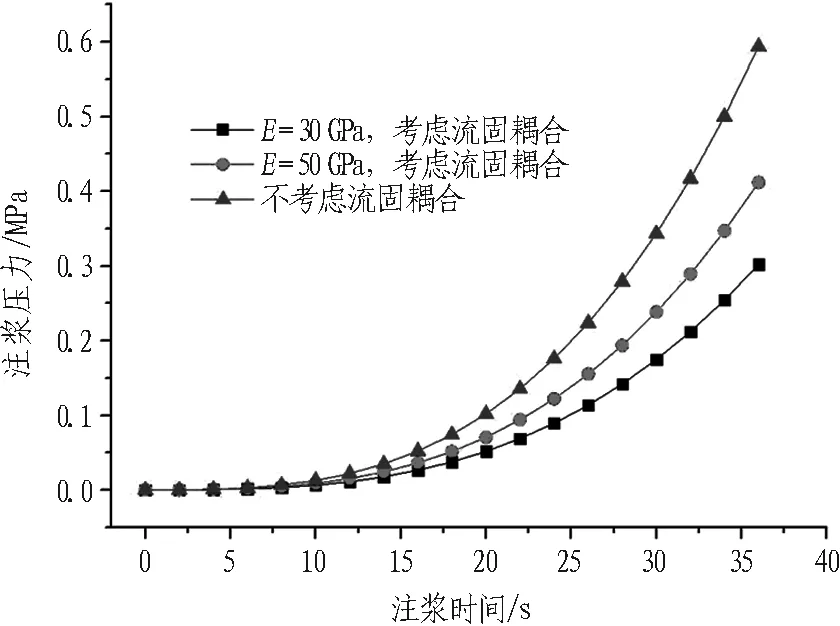
(b) b=0.1 mm

Fig. 7 Grouting pressures with and without consideration of fluid-solid coupling

不考慮流固耦合效應時，由于裂隙開度維持不變，漿液擴散阻力相比實際情況偏大，達到相同漿液擴散半徑時對應的注漿壓力也相應偏大。當裂隙開度較小時，考慮與不考慮流固耦合效應所引起的注漿壓力數值差別更大，不考慮流固耦合效應時注漿壓力的計算誤差可達到30%以上。

4.2 漿液擴散半徑方面

相同注漿壓力條件下，考慮與不考慮流固耦合效應所得漿液擴散半徑的大小對比如圖8所示。

不考慮流固耦合效應時，漿液擴散阻力相比實際情況偏大，相同注漿終壓條件所對應的漿液擴散半徑偏小。當裂隙開度較小、巖體彈性模量較小時，考慮與不考慮流固耦合效應所引起的注漿壓力數值差別更大，不考慮流固耦合效應時注漿擴散半徑的計算誤差可達到15%以上。

通過以上分析可知，不考慮流固耦合效應計算得到的注漿壓力明顯偏高，漿液擴散半徑明顯偏低，故在注漿設計中應充分考慮流固耦合效應對注漿擴散過程的影響。

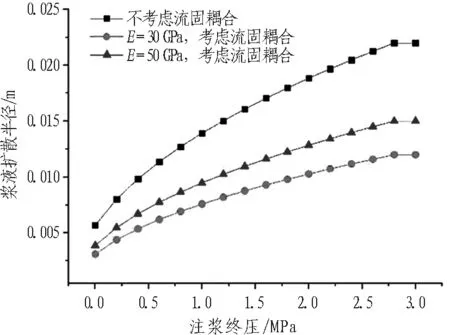
(a) b=0.3 mm

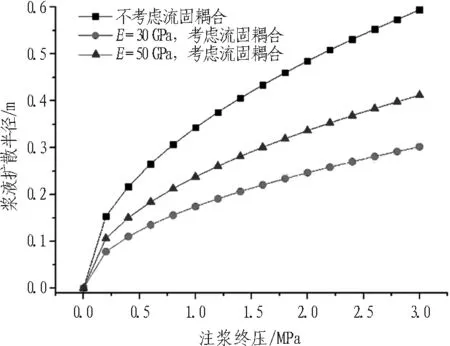
(b) b=0.1 mm

Fig. 8 Grout diffusion radius with and without consideration of fluid-solid coupling

5 結論與討論

1)綜合考慮漿液流場與圍巖變形之間的耦合作用，建立了考慮流固耦合效應的單一裂隙注漿擴散有限元計算模型，實現了注漿擴散過程的動態模擬。

2)注漿壓力由注漿孔向漿液擴散鋒面方向非線性衰減，導致注漿孔附近圍巖應力相對集中，注漿孔附近區域最先發生塑性破壞。

3)裂隙開度由注漿孔附近向漿液擴散鋒面處衰減，這與漿液壓力的空間衰減相對應，注漿壓力非線性增長。

4)在微裂隙巖體注漿中，不考慮流固耦合效應時注漿壓力的計算誤差可達到30%以上，注漿擴散半徑的計算誤差可達到15%以上，所以在注漿設計中應充分考慮流固耦合效應對注漿擴散過程的影響。

5)由于巖體裂隙發育情況復雜，很難通過單一的裂隙注漿計算結果來表征整個巖體裂隙網絡的注漿擴散情況，這方面還有待于開展進一步的研究。