循環荷載下膠凝砂礫石材料的滯后及阻尼效應

黃 虎, 黃 凱， 張獻才， 韓立煒

(1.華北水利水電大學 水利學院， 河南 鄭州 450045； 2.河南省水工結構安全工程技術研究中心， 河南 鄭州 450045； 3.河南省豫東水利工程管理局三義寨分局， 河南 開封 475000)

膠凝砂礫石(cemented sand and gravel, CSG)材料是一種將水、膠凝材料、河床砂礫石或開挖廢棄料等當地材料混合，然后利用簡易設備和工藝進行拌和后得到的新型筑壩材料.近年來，CSG壩在希臘、日本、土耳其[1-3]都有所應用.2004年，中國在貴州省松道塘水庫上游過水圍堰工程中首次采用 CSG壩方案，此后在福建白沙、街面和洪口3個水電工程中的上、下游圍堰相繼采用.隨著近年來大量理論成果的進展，2014年，中國第一座永久性CSG建筑物——守口堡大壩在山西省開工建設.目前，國內外在CSG材料的靜力學特性和本構模型研究方面取得了大量有價值的成果，但關于其動力學性能方面的研究主要集中于材料的動模量和阻尼比.Omae等[4]采用動三軸儀測試了Takizawa壩的筑壩材料動力性質，認為在小幅值循環壓力作用下，CSG材料的動剪切模量隨圍壓增大而增大，材料動力本構關系表現出明顯的非線性性質，隨著剪應變增大，材料動剪切模量減小.Haeri等[5]通過不排水動三軸試驗研究，認為水泥含量對CSG材料的最大剪切模量和阻尼比影響不大；隨著偏應力的增大，材料的阻尼比增大而剪切模量降低；圍壓越大，材料的剪切模量越大而阻尼比越小.明宇等[6]采用大型動三軸試驗研究了不同膠凝材料摻量下CSG材料的動力特性，給出了膠凝材料摻量、圍壓對CSG材料動力特性影響的變化規律，推導了非線性動彈性模量及阻尼比的表達式.傅華等[7]通過對不同膠凝材料摻量的CSG材料進行動三軸試驗，發現其動力學指標隨著膠凝材料摻量和養護齡期的增加得到了一定提高；隨著圍壓、固結應力以及動應力的提高，其動永久變形量相應增大.蔡新等[8]基于動三軸試驗，研究了不同圍壓、不同膠凝材料摻量下CSG材料的動本構關系及動模量衰減規律.

以上文獻對CSG材料阻尼比變化規律的研究主要集中在小應變狀態下，而對循環加載過程中應力-應變的滯后關系、滯回環演化規律鮮有提及.根據相似材料的研究經驗[9-10]，循環荷載下材料的變形和破壞是一個損傷不斷產生、累積的過程，也是能量不斷耗散的過程，而耗散能的變化可以從滯回環的演化入手；滯回環的形態不僅反映了循環加卸載過程中力和變形、阻尼等特性，同時材料的動彈性模量、阻尼比、能量耗散等動力學參數也是通過滯回環求得的.Tutuncu 等[11-12]利用單軸應力循環試驗分析了影響沉積巖非線性彈性行為的一些主要因素，認為滯后機制是由于裂紋表面和顆粒邊界之間的摩擦滑動引起的.肖建清等[13]通過花崗巖常幅循環加載試驗，探討了滯回環可能存在的形態，認為滯回環形態有橢圓形、新月形和長茄形，主要取決于應變相位和應力相位的關系.何明明等[14]通過常幅循環荷載試驗揭示了阻尼比隨循環次數的演化規律，認為應力上限會影響阻尼比的發展規律，在加卸載過程中阻尼比隨著循環次數的變化而變化.從CSG材料自身的特性來看，受到砂礫石形狀和低摻量膠凝材料的影響，其自身孔隙率遠大于常規土體和巖石，動力學特性也與一般材料存在差別.要想充分認識CSG材料的動力學性能，探明其在動荷載下的滯回環及相應動力學參數的演化規律，需要從CSG材料在循環荷載下的滯后特性和滯回環入手，研究整個循環過程中材料參數的變化規律.本文利用大型動三軸試驗系統，對循環荷載下CSG材料的滯后特性進行了研究和分析，根據滯回環的特征和演化規律，基于能量原理對新月形滯回環的阻尼比進行了討論，得出了整個循環過程中CSG材料的阻尼比演化規律，為進一步認識CSG材料的動力學特性奠定基礎.

1 試驗

1.1 試驗材料

CSG試件由水泥、粉煤灰、砂礫石和水按一定比例混合制備而成.水泥采用普通硅酸鹽水泥；根據GB/T 50146—2014《粉煤灰混凝土應用技術規范》對粉煤灰品質的要求，粉煤灰采用中國鄭州熱電廠干排F類 Ⅱ 級粉煤灰，比表面積為506m2/kg；砂礫料取自汝州市汝河河床，為減小因材料不均勻而造成試件力學特性波動太大的影響，將砂礫石混合料篩分，以便優選砂率進行配合比試驗，骨料采用二級配；水為自來水.根據SL 678—2014《膠結顆粒料筑壩技術導則》，膠凝材料用量不宜低于80kg/m3，其中水泥熟料用量不宜低于32kg/m3，水膠比(mW/mB)宜控制在0.7～1.3，膠凝砂礫石中砂率(質量比)宜為0.18～0.35.試驗采用的CSG材料配合比設計參數見表1.

1.2 試件制備及試驗設備

CSG試件為φ150×300mm的圓柱體，將砂礫石、水泥、粉煤灰和水按表1所示配合比放入攪拌機攪拌均勻，裝入鋼模具內，采用人工結合機器的振搗方式，48h后成型脫模，置于標準養護室內養護至規定齡期(28d).

試驗設備采用美國GCTS公司生產的 STX-600 型動三軸儀，該儀器由液壓站、數字信號調節控制單元、荷載架和三軸壓力室、壓力/體積控制器以及CATS軟件5部分組成.荷載架最大可以提供300 kN 的軸向力，三軸壓力室可以承受最大 2 MPa 的壓力.

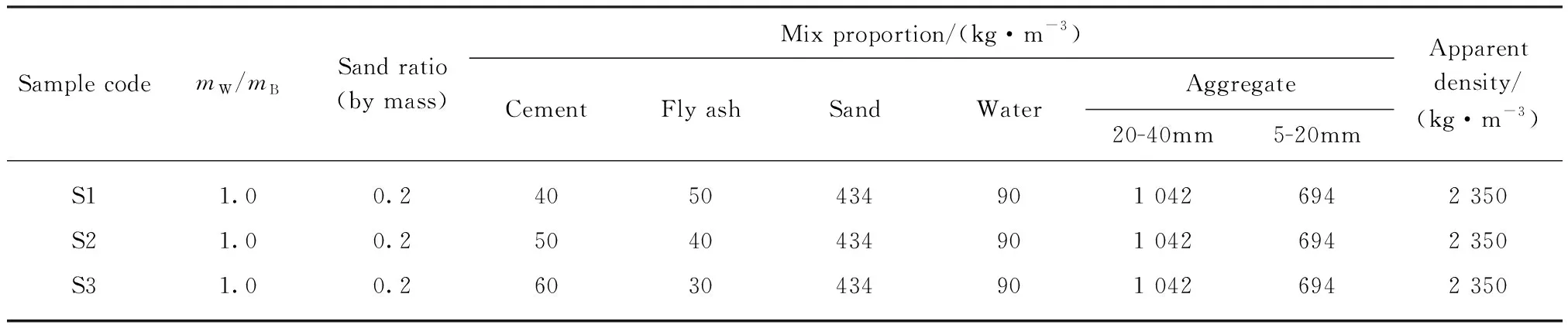
表1 CSG試件配合比設計參數

1.3 試驗加載方式

考慮水利工程遇到的動荷載類型主要為地震和波浪荷載，加載波形設為正弦波，頻率為1.0 Hz.根據靜力學試驗結果[15]，材料的彈性極限強度為其峰值強度σd的75%，因此，為了得到足夠的循環次數，等幅循環試驗的上限循環應力σup控制在75%σd以下；選定3組應力水平，以等幅值的正弦波方式施加循環荷載，直至試件破壞，記錄荷載的循環次數；當試件應變達到10%時停止.

2 非線性滯后特征分析

2.1 累積應變與循環次數關系

CSG材料的峰值強度與水泥含量有密切關系，水泥含量越大，材料峰值強度越大[16].故根據水泥含量不同，試驗時上限循環應力σup取試件σd的 50%～ 70%.圖1是各試件在循環荷載下的累積應變和循環次數關系曲線.由圖1可知，各試件的應變均表現出三階段特征：初始階段、等速階段和加速階段.每個階段在整個循環中的長度不同，初始階段最小，出現在前3個循環，此時變形速率迅速衰減；等速階段循環次數最多，變形速率基本為恒定值，該階段的長短與加載的上限循環應力大小密切相關，上限循環應力越小，等速階段越長；當應變接近臨界破壞應變時，變形速率迅速增大，循環進入加速階段，經歷兩三個循環后，試件破壞.

圖1 各試件在循環荷載下的累積應變與循環次數關系Fig.1 Accumulated strain-cyclic number curves of samples

從整個應變的變化過程看，不同階段間存在明顯的臨界應變值，且臨界應變值與水泥含量及上限循環應力的大小密切相關.從每個階段經歷的循環次數看，初始階段的循環次數相同；在等速階段，上限循環應力越接近75%σd，循環次數越少，加速階段循環次數也越少，試件達到臨界破壞應變后破壞越迅速.水泥含量越高，試件的臨界破壞應變越大.

2.2 非線性滯后分析

基于上述累積應變分布的三階段劃分，以試件S1為例，對不同上限循環應力下不同應變階段的應力-時間和應變-時間曲線進行歸一化處理，如圖2所示(其中L01，L02等分別表示第1個，第2個等滯回環).由圖2可見：在整個循環過程中，應力與應變曲線并不重合，在循環的加載階段，應變曲線一部分超前于應力曲線，應力與應變的相位差為負值，而應變曲線的另一部分滯后于應力曲線，兩者相位差為正值，且與循環次數有關；在循環的卸載階段，應變曲線滯后于應力曲線，應力與應變之間的相位差為正值.應變曲線在第1個和最后1個循環出現了明顯改變，呈非正弦分布.

圖2 試件S1的應力-時間和應變-時間曲線Fig.2 Stress-time and strain-time curves of sample S1

在不同階段，單個滯回環的應力峰值和應變峰值的相位差表現出不同的特征，可能為零，也可能為正值.如果應力與應變的相位差為零，說明應力與應變的相位相同，表明材料是線彈性的，且不存在滯后現象；如果應力與應變的相位差不為零，則表明在循環荷載作用下材料產生了滯后效應，相位差的大小表現了材料偏離線彈性性質的程度和產生滯后效應的強弱[17].圖2中，試件S1在初始階段的應變峰值滯后于應力峰值，應力與應變的相位差為正值且逐漸減?。辉诘人匐A段前期，二者相位差仍為正值，并逐漸減??；當接近總循環次數的一半左右時，應變峰值與應力峰值幾乎重合，二者相位差為零，隨后，應變峰值滯后于應力峰值的程度又逐漸增大；當進入加速階段后，應變峰值滯后于應力峰值的現象越來越明顯，應力峰值和應變峰值的相位差迅速增大，在試件破壞前的1個循環，應變曲線與應力曲線不再保持一致，滯后現象突出.從試件S1的整個循環過程來看，隨著循環次數的增大，加載階段應變與應力相位差為負值的部分由大—小—大，當應力峰值與應變峰值的相位差為零時，對應循環加載段的應變與應力相位差全部為負值，這與單個循環滯回環產生的塑性變形密切相關，單個循環的塑性變形越大，應變滯后于應力的程度越大.根據分析結果，試件S2，S3的應力、應變與時間關系也存在相同的特征，限于篇幅限制，這里不再給出具體的結果.

由于CSG材料中骨料形狀的不規則，加上低含量的膠凝材料不能完全充填骨料間的縫隙，使得材料內部分布著許多裂紋、孔洞以及微結構邊界，從而導致了其非線性彈性行為和顯著的滯后特征.當上限循環應力與峰值強度的比值較小時，在一定時期內，試件處于壓實過程，試件內部空隙和微裂紋逐漸閉合，并產生塑性變形，且該變形隨著循環次數的增加而逐漸減小；當壓實到一定程度后，試件內部新微裂紋萌生，新的塑性變形出現，且隨著新微裂紋的發展和貫通而逐漸增大，當接近試件的疲勞壽命時，塑性應變達到最大.當上限循環應力與峰值強度的比值較大時，由于上限循環應力接近試件的屈服強度，試件內部原始微裂紋的閉合過程與新微裂紋的產生過程沒有明顯的分界點，存在重疊期，從而使整個循環過程中的塑性變形均較大，應變峰值始終明顯滯后于應力峰值.前1次循環的塑性變形導致當前循環加載段的應變超前于應力，而當前循環過程中產生的塑性變形導致卸載段應變滯后于應力.

圖3給出了等速階段中各試件在不同上限循環應力下單個滯回環所對應的塑性應變.由圖3可知：隨著循環次數的增加，單個循環的塑性變形均先減小后增大，即滯回環下部開口先減小后又增大；當上限循環應力較小時，塑性應變的最小值接近零，滯回環幾乎閉合；當上限循環應力較大時，滯回環張開明顯.累積塑性應變整體呈增大的趨勢，說明塑性應變的存在是導致加載段應變相位超前于應力相位的根本原因.

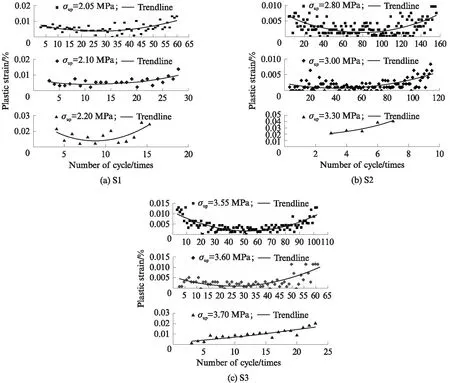
圖3 單個循環塑性應變分布Fig.3 Plastic strain distribution of single loop

2.3 滯回環形態分析

由于CSG材料自身結構特點的影響，在循環加載過程中幾乎每個循環都會有塑性變形產生，從而造成滯回環的不閉合.圖4給出了各試件在不同應變階段的單個滯回環形態.由圖4可以看出，初始、等速和加速階段滯回環下部的不閉合程度不同，初始階段和加速階段較大，說明在開始和結束前的幾個循環中，塑性變形以及消耗的能量都比較大.

圖4 試件S1，S2，S3的典型滯回環Fig.4 Typical hysteresis loops of sample S1, S2, S3

在1個完整循環周期內，若應變始終滯后于應力，則滯回環呈橢圓形；若加載段應變超前于應力，卸載段應變滯后于應力，則滯回環呈新月形；若加載段應變既有滯后于應力部分，也有相等和超前部分，則滯回環呈長茄形[13].根據以上分析，CSG材料的應力相位與應變相位在加載段和卸載段存在明顯不同，應力與應變相位差在加載和卸載時并不相等，這說明滯回環頂部應力方向反轉時刻對應的應變相位進行了調整，因此應力-應變滯回曲線在荷載反轉處是尖葉狀的，不是橢圓形的，滯回環為新月形，向應變增大的方向凸出.滯回環的形態不僅取決于加卸載過程中的塑性變形，還受到材料黏滯性的影響，而材料黏滯性主要受到其內部液體和顆粒摩擦的影響.本試驗過程中的試件均為干燥試件，故可忽略內部水產生的黏滯作用.但從各試件滯回環的演化過程來看，除了加載的第1個循環外，隨著循環次數的增加，初始階段和等速階段的新月形滯回環均比較扁薄，在接近破壞前的幾個循環逐漸趨于寬厚，滯回環的頂部由尖葉狀向橢圓形變化，說明破壞前的滯回環受到材料黏滯性的影響較大，主要原因是試件破壞前內部出現了大量裂紋，導致膠結鍵斷裂，骨料間的摩擦使材料表現出了黏滯性.材料黏滯性對滯回環的影響在試件內部出現大量裂縫以后表現明顯.

2.4 滯回環的描述

為分析每個滯回環的演化規律，根據單個滯回環加卸載段的應力-應變關系，將試驗數據采用分段的方式進行描述.限于篇幅限制，以試件S1，上限循環應力σup為2.05MPa時的典型滯回環為例，將每個滯回環分為加載段和卸載段，對各段曲線進行擬合(見圖5)，進而描述循環過程中加卸載段的應力-應變關系.

圖5 試件S1的典型滯回環擬合曲線Fig.5 Fitting curves of typical hysteresis loops of sample S1 (σup=2.05MPa)

由圖5可知，對于不同的單個滯回環而言，加卸載段應力-應變均可描述為以e為底的指數函數，即：

(1)

式中：σ為單個循環的應力；ε為單個循環的應變；a，t，b為擬合參數.

典型滯回環加載段和卸載段的擬合參數a，t，b與循環次數的關系如圖6所示.由圖6可知：隨著循環次數的增加，擬合參數呈非線性減??；在循環初期擬合參數的減小速率較大，經歷20個循環后，擬合參數的減小速率逐漸變??；隨著循環次數的增加，同一參數在加載段的變化幅度大于卸載段；t的變化速率明顯小于a和b.

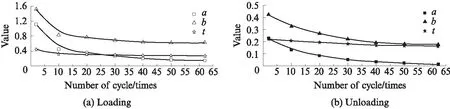
圖6 加卸載段擬合參數與循環次數關系Fig.6 Fitting parameters and cycle number curves

3 阻尼比分析

阻尼比是進行材料動力反應分析時必不可少的參數之一，是衡量材料吸收振動能力的一個重要指標.DL/T 5355—2006《土工試驗規程》針對對稱性橢圓形滯回環的阻尼比(λ)給出了如下的計算公式：

(2)

式中：A為滯回環的面積，表示單個循環消耗的能量；As為峰值應力、對應應變和橢圓中心圍成的面積，4As表示1個周期內所儲備的最大彈性應變能.

目前針對巖土和混凝土材料的阻尼比大多基于式(2)進行計算，由于新月形和長茄形滯回環上下左右都不對稱，因此嚴格意義上并不符合式(2)的前提條件.

從能量角度出發，在循環加載過程中，吸收的能量一部分形成彈性應變能，另一部分則以聲能、熱能、輻射能以及新塑性區產生所需要的能量等形式消耗掉，即耗散能，損耗的能量一部分用于微裂紋的萌生和擴展，一部分用于克服阻尼力做功.能量耗散是反映材料內部微缺陷不斷閉合、新裂紋萌生和發展演化的本質屬性.根據能量守恒原理，假設材料單元在外力作用下產生變形時與外界沒有熱交換，則外力功產生的總輸入能量U為：

U=Ue+Ud

(3)

式中：Ue為可釋放的彈性應變能；Ud為單元耗散能.

根據上述滯后性分析，在加卸載過程中，CSG材料在不同循環中存在不同的滯后效應，其在循環加卸載過程中的典型滯回環曲線見圖7.其中：加載階段的應力極值點為B點，應變極值點為C點；卸載段的應力極值點為D點，應變極值點為E點.由圖7可見，應力極值和應變極值不同步，滯回環不閉合，存在滯后和殘余變形，且滯后程度和殘余變形隨著循環次數的增加而變化.在循環加載過程中，從A點至B點的加載段，試件的應力、應變都在增大，外力對試件做正功；達到B點后，試件的應力減小，但是由于滯后效應，其應變繼續增大至C點，故BC段的變形仍然是外力對試件做正功；從C點開始，試件的應變開始減小，直到D點，其應力、應變都減小，試件向外釋放彈性應變能，外力對試件做負功；達到D點后，試件的應力反向增大，但是由于滯后效應，其應變繼續減小，直至達到下限應變極值E點，因此，DE段的變形仍然是外力對試件做負功.

圖7 循環加卸載典型滯回環曲線Fig.7 Typical hysteresis loop under cyclic loading and unloading

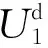
針對單個滯回環，將加卸載方程(1)代入式(3)，得到單個滯回環的耗散能，即：

(4)

根據阻尼比的定義，式(2)可修改為耗散能與彈性應變能之比再除以π，即：

(5)

采用式(5)得到各試件的阻尼比演化曲線如圖8所示.由圖8可見，阻尼比曲線也可分為3個階段，整體上呈U型：第一階段阻尼比快速下降，阻尼比位于0.025～0.090之間，特別是第1個循環的阻尼比最大；經歷3個循環后，進入第二階段，阻尼比位于0.025～0.035之間，此時阻尼比呈先下降后上升的拋物線形分布；當進入第三階段后，阻尼比又快速增大，阻尼比位于0.030～0.100之間，且在試件接近破壞時呈陡然上升趨勢.同時上限循環應力和水泥含量對試件的阻尼比存在一定影響，水泥含量相同試件的上限循環應力越大，其阻尼比越大.

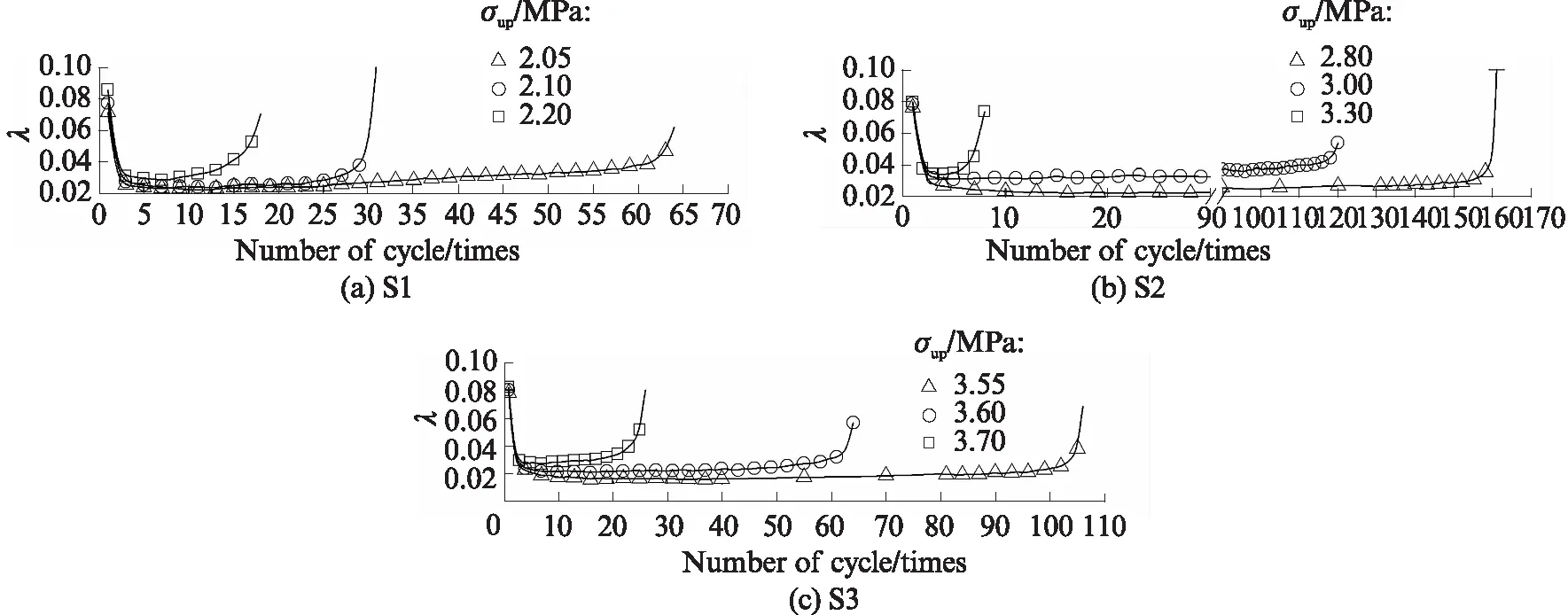
圖8 各試件的阻尼比演化曲線Fig.8 Evolution curves of damping ratios for different samples

在加載初期的第一階段，試件處于初期壓密狀態，直觀表現為滯回環的面積和底部張開相對較大，殘余變形和能量消耗較大(第1個循環尤為突出)，由此形成的阻尼比也較大.第二階段，由于試驗為等幅循環加載，同一上限循環應力下，總能量輸入基本相當，每個滯回環的面積也基本相同，試件的塑性變形隨著循環次數的增加而變化(見圖3)，從而使阻尼比隨其塑性變形(單個滯回環的殘余變形)的變化而變化.第三階段，由于試件臨近破壞，內部出現了大量裂縫，滯回環塑性變形增大，微結構面間的摩擦消耗了大量的能量，特別是破壞前1個循環，以致于形成了較大的阻尼比.

綜上，每個循環都存在不同程度的殘余變形，能量的耗散一部分用于克服阻尼力做功，一部分用于殘余變形的產生，故殘余變形對阻尼比的影響不可忽視；阻尼比的大小由殘余變形和滯回環面積共同決定，同時殘余變形還影響了阻尼比在整個加卸載過程中的變化形態.在試驗過程中第一階段和第三階段歷時較短(一般在3個循環左右)，在工程實際應用時，由于固結沉降作用可使材料內部的部分原始缺陷處于閉合狀態，因此在不考慮極限使用狀態的情況下，可參考第二階段的阻尼比取值，即認為膠凝砂礫石材料的阻尼比位于0.025～0.035之間.

4 結論

(1)在循環荷載作用下，膠凝砂礫石材料表現出明顯的非線性滯后特征.在加載階段，由于塑性變形的存在和累積，以及試件自密實的影響，使其應變有部分超前于應力，而另一部分則滯后于應力，兩者相位差與循環次數有關；在卸載階段，由于阻尼力的存在，應變相位滯后于應力相位，且滯后程度在試件破壞時達到最大.

(2)根據加卸載過程中應力與應變的滯后關系，在循環荷載作用下膠凝砂礫石材料的滯回環為下部不閉合的新月形，不閉合程度反映單個滯回環塑性變形的大小，且隨著循環次數的增大呈大—小—大的變化趨勢；當試件接近破壞時，受到黏滯作用的影響導致新月形頂部由尖葉狀趨向于橢圓形.

(3)鑒于膠凝砂礫石材料滯回環的特點，基于能量的方法討論了其阻尼比演化規律.結果表明:阻尼比呈U型分布，阻尼比與滯回環的面積及殘余變形正相關；在正常使用狀態下，可認為膠凝砂礫石材料的阻尼比為0.03.