交通運輸對人力資本的影響分析1
——基于動態一般均衡理論
王貴東
0 問題的提出
2014年,中國將京津冀的協同發展上升為國家戰略。對于北京,與上海一樣,是中國人力資本非常發達的城市,集聚了大批高端人才,涌現出大量科研成果;但京津冀城市群和長三角城市群的發展卻迥然不同:由于北京的虹吸效應大于涓流效應,甚至出現了環首都貧困帶;而上海則涓流效應大于虹吸效應,惠及了整個長三角。對于這種奇怪現象,國內一度出現了研究熱潮,但多數文獻為“分析現象+政策建議”式研究(趙奇偉和張誠,2006;姜玲等,2010;郭曄,2010;蓋美等,2013;李磊和張貴祥,2015)。對于現象背后的原因,學界并沒有達成共識,目前仍是一大研究難題,僅有的一些文獻試圖從中國制度、歷史演進(孫久文和原倩,2014),以及總部經濟(梁琦等,2012)等方面分析其原因。
透過現象看本質,京津冀與長三角人力資本的分岔現象僅是中國的一個縮影,本文的研究對象則是更為抽象的不同地域[注]每個地域都可以看作一個城市群系統。,及不同地域人力資本差異的產生原因。本文的理論模型為新古典經濟增長模型,該模型由Solow(1956)開創。雖然早在1960年, Schultz(1960)就已經提出了現代人力資本理論。但直到1980年代中期,Romer(1986)、Lucas(1988)才基于人力資本開創性提出了內生經濟增長理論。 Romer(1990)認為人力資本可以促進技術進步,推動經濟內生增長;而Lucas(1988)則認為人力資本的外溢性導致了地區經濟差異和增長發散。在實證方面,多數國內學者將人力資本作為參數,研究其對經濟和社會的影響,如研究人力資本對經濟增長的作用(賴明勇等,2005;錢曉燁等,2010;朱承亮等,2011;逯進和周惠民,2013),對員工工資差異、員工職業成功的作用(張車偉和薛欣欣,2008;周文霞等,2015),對非自愿移民的影響(石智雷等,2011)等。然而,如果僅單向地研究人力資本對經濟和社會的影響,則相當于把人力資本作為外生變量,甚至可以得出一個極端:只要提高人力資本,就可持續刺激經濟增長。為了避免此種極端,在技術層面上,可以考慮人力資本的獲取成本、折舊等。而本文則是利用一般均衡框架,通過市場手段來約束人力資本,故本文的人力資本是內生的。在人力資本的眾多影響因素中,本文認為交通運輸是破解中國人力資本地域差異的一個重要突破口,并且具有很強的時代意義[注]近幾年,中國政府機構最大的調整莫過于鐵道部的分拆,中國電商的繁榮突起得惠于強大的互聯網平臺和交通物流平臺支撐,中國高鐵也逐漸成為了中國的國家名片等,這些無一不與交通運輸相關。。同時,中國地域遼闊、地形復雜,既有平原地區,也有高原、山地、沙漠等地區,這些自然稟賦無疑會影響甚至決定交通道路的宏觀布局。
在具體模型構建中,鑒于中國政府已從重視經濟增長向重視經濟結構調整轉變,經濟結構的合理性主要反映在產業結構上,且經濟活動的主要場所為城市,故本文的經濟系統將涵蓋城市和產業兩大基本領域。其中,城市借鑒了單中心城市理論,即中心—外圍結構;產業主要指縱向產業,即產業鏈的上下游關系。當然,為了研究交通運輸對經濟系統的影響,并給出運輸成本與人力資本的相互關系,在技術上本文還引入了Samuelson冰川模型。
本文其余部分安排如下: 第1部分為模型介紹,主要從消費者和生產者兩方面展開。第2部分為均衡分析,研究了運輸成本對穩態人力資本的影響。第3部分為實證檢驗,利用2005—2014年中國31個省(區、市)數據,以SARAR(Spatial Autoregressive Model with Spatial Autoregressive Disturbances)、WSARAR(Weighted SARAR)作實證檢驗。最后為結語與啟示,并拓展分析了運輸成本的空間、時間以及社會屬性。
1 模型介紹
本文理論模型主要借鑒于Black and Henderson(1999),并進行了拓展,具體包括:(1)城市空間結構。城市空間結構由原來的人口密度處處相等,拓展為距離市中心越近人口密度越大。(2)運輸成本。將Samuelson冰川模型引入中間投入品市場。下面,將從消費者和生產者兩方面來闡述模型的一些基本情況。
1.1 消費者
按照Black and Henderson(1999)的假設,家庭成員生活在兩種城市。第一種城市處于產業鏈上游,生產中間投入品,不妨稱其為城市1。第二種城市處于產業鏈下游,生產最終消費品,不妨稱其為城市2。在每個家庭中,城市1的成員比重為z,則城市2的成員比重為1-z。那么,作為消費者,“綜合”代表人最大化家庭效用決策為
(1)
其中,c為消費;1/σ為不同時點的消費替代彈性,1-σ為效用的消費彈性,滿足σ>0;ρ為時間貼現率,g為人口增長率,滿足ρ>g。下標1、2分別代表城市1、城市2,I為收入,h為人力資本,P為最終消費品的價格。式(1)的隱含意義為:在家庭內部,家庭成員的收入會有所不同,但家庭成員(尤其是高收入的家庭成員)并不是以自身效用最大化,而是以家庭效用最大化。
需要說明的是,由于本文理論模型為動態模型,故消費c、人力資本h、最終消費品價格P等變量實際為時間t的函數,即c(t,·)、h(t,·)、P(t,·)。為了使本文表達式更具簡潔性,這里將省略時間t;而在后文也作相應處理,文后不再一一說明。
1.2 生產者—城市1
在城市1中,假設居民既是消費者又是企業本身,并且代表人i的生產函數為
(2)
其中,n1為城市1的企業數量(人口規模),h1為城市1的行業平均人力資本,h1i為企業i的人力資本。δ1為企業數量彈性,表示企業數量的外部性,側重于數量方面的外部性。ψ1為平均人力資本彈性,表示人力資本的外部性,側重于質量方面的外部性。θ1為企業i的人力資本彈性。
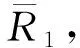
其中,b1≡τ[(2-β1)/(3-β1)][(2-β1)/(2π)]1/(2-β1)。
利用前面獲得的總通勤成本TCommuting1和總地租TRent1,可以分析城市1的居民收入I1。不妨將中間投入品的價格標準化為1,可以得到企業i的收益W1i=X1i。而在城市中生活,居民需要支付必要的通勤成本和地租,同時也能獲得城市管理者的轉移支付,所以居民的最終收入為:
I1=W1+T1-(TRent1+TCommuting1)/n1
現在分析城市管理者的決策,城市管理者收取租金,然后通過轉移支付形式返還給居民。具體為城市管理者宣布城市類型為城市1,選擇城市人口和轉移支付來最大化TRent1-n1T1。

(3)
其中,η1≡1-(2-β1)δ1,δ1<1/(2-β1)[注]因為對于個人,產出的人口規模彈性為δ1,成本的彈性為1/(2-β1)。當δ1>1/(2-β1)時,隨著人口的增加,產出增加的比例高于成本,城市1的人口會不斷膨脹,直到世界上只剩下一個城市,這顯然與現實矛盾,所以δ1<1/(2-β1)。;ε1≡(ψ1/η1)+φ1,φ1≡θ1/η1,φ1<1;Q1≡η1{[(1-η1)/b1]1-η 1D1}1/η 1。最后,綜合城市1中所有已得的關系式,可以得到
其中,式(5)第二個等號需要將式(3)代入W1并整理。
1.3 生產者—城市2
在城市2中,假設居民既是消費者又是企業本身,并且企業j的生產函數為:
(6)
在式(6)中,n2為城市2的企業數量(人口規模),h2為城市2的平均人力資本;h2j為企業j的人力資本;x1j為企業j需要的中間投入品數量。δ2、ψ2、θ2、1-α分別為企業數量、平均人力資本、企業j的人力資本、中間投入品彈性。同時,α還滿足邊際報酬遞減規律,即α<1。(特別地,對于零售企業,由于存在倉庫等其他要素投入,故中間投入品x1j仍要滿足邊際報酬遞減規律,即α不能取到0)
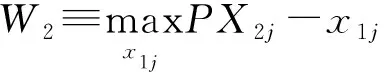
(7)

(8)
其中,η2≡α-(2-β2)δ2,0<η2<1;ε2≡(ψ2/η2)+φ2,φ2≡θ2/η2,φ2<1;Q2≡η2{(1-α)(1-α)[(α-η2)/b2]α-η 2D2}1/η 2。最后,綜合城市2中所有已得的關系式,可以得到
其中,式(10)第二個等號需要將式(8)代入W2并整理。
2 均衡分析
由式(1)構造“綜合”代表人的現值Hamilton方程:
(11)
由式(12)、式(13)可知,當ξ1<ξ2時,城市2的平均人力資本、收入均高于城市1;反之亦然。
2.1 中間投入品市場
接下來,分析中間投入品的市場均衡。令m1、m2為城市1、城市2的數量,N為所有城市1和城市2的加總人口。假設中間投入品既是城市2中企業的生產要素,又能支付城市1、城市2中居民的通勤費用。需要說明的是,Black and Henderson(1999)并沒有考慮到中間投入品從城市1運輸到城市2所產生的運輸成本。而本文試圖引入運輸成本,進一步拓展該模型。在技術處理上,本文采用Samuelson的冰川模型形式來描述運輸成本,即只有1/μ的中間投入品送達城市2,其中μ≥1,運輸成本越高,則μ越大;當運輸成本完全將為零時,μ=1。那么,中間投入品的市場均衡為
(1/μ)m1n1[X1i-(TCommuting1/n1)]=m2n2[x1j+(TCommuting2/n2)]
(14)
很明顯X1i-(TCommuting1/n1)=I1,又由式(9)得x1j+(TCommuting2/n2)=[(1-η2)/η2]I2;再結合式(13)和m1n1/m2n2=z/(1-z),可得
(15)
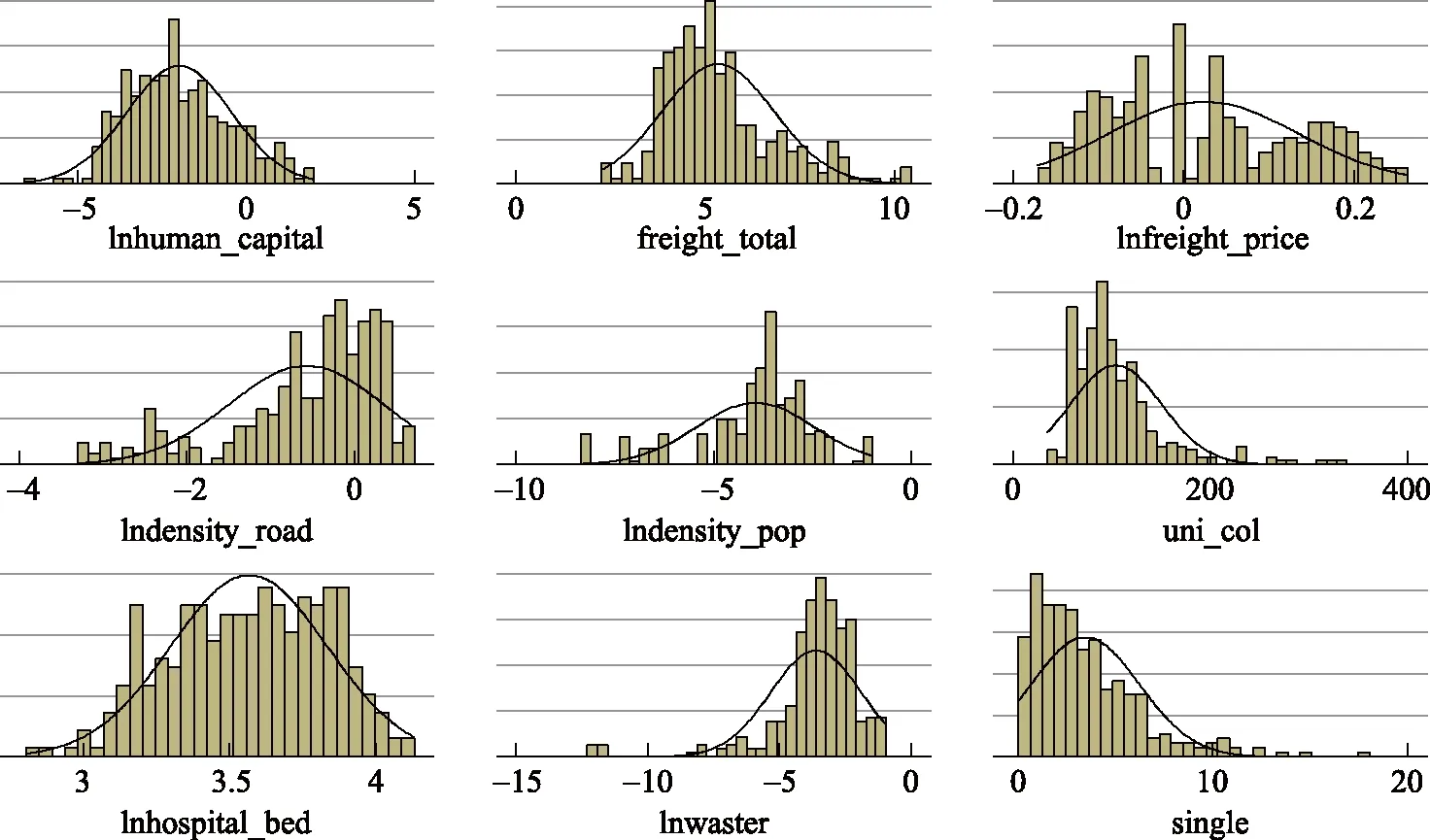
其中,E≡μξ1(1-η2)+ξ2η2,F≡μ(1-η2)+η2,E 另外,把式(15)代入h=zh1+(1-z)h2,并結合式(12)可得 (16) 其中,K≡(F-E)/E。將式(16)代入式(5)、式(10)后,結合式(13)可得 (17) 接下來,分析系統穩態。根據式(5)、式(10)、式(11)、式(16)、式(17)可得 其中, (20) (21) 下面,將研究運輸成本對鞍點的影響,式(20)結合前面所有關系式可得 (22) 另外,將式(20)代入式(16),可得 (23) 式(23)揭示了運輸成本如何影響人力資本穩態值,不難發現運輸成本僅通過z間接影響人力資本的穩定值。也就是在整個經濟體地域內,一些城市直接從城市1轉型為城市2或城市2相對于城市1更迅速的人口增長,均能促使該經濟體人力資本的穩態值增加,而運輸成本正是這個引擎。 本文的運輸成本,主要指經濟體內部不同點之間相互運輸,不包括“過路型”運輸(比如從廣州運往哈爾濱會經過河北省等)。現在,可回到本文一開始對京津冀(或長三角)的討論,并回答產生人力資本差異的原因:①對于京津冀,其發達的交通是毋庸置疑的,鐵路的八橫八縱有5條以北京為起始點,1開頭的所有國道均以北京為起始點。但如果將河北作為一個經濟體,會發現京津冀“輻射型”干道只是表面上的交通發達,河北自身則非常不方便。這是因為中間投入品從河北的城市A到河北的城市B,往往缺少直接相連的主干道,反而得繞行北京中轉,這無疑增加了運輸成本(既有貨幣成本也有時間成本)。根據本文命題可知,較高的運輸成本將限制河北的人力資本發展。另外,河北甚至還充當了“過路型”運輸的角色。②對于長三角,其交通同樣比較發達,但卻與京津冀的類型完全不同,長三角的交通多為“隨機型”干道,上海、蘇州、杭州、無錫、常州等城市兩兩之間幾乎都有多條干線相連。那么根據本文命題,長三角由市場內生決定的人力資本必然會很高(即使剔除了上海)。所以對于京津冀問題,若要提高河北的人力資本,則必須在河北內部投入更多的道路建設,而不是大力規劃河北與北京[注]一定程度上還會造成北京的擁堵。之間的道路建設,這將會是京津冀協同發展的一個重要誤區![注]北京的交通樞紐完全可以由河北某城市或天津進行分擔,這樣就不會出現原本目的地非北京,但必須經過北京中轉的現象。2015年底,津保鐵路的連通則是一個很好的例子,從保定到秦皇島不再繞行北京,可直接經過天津中轉,降低了保定到秦皇島的成本(既有貨幣成本也有時間成本)。 在實證檢驗部分,本文將利用中國數據來檢驗理論模型命題的正確性,即檢驗運輸成本與人力資本和消費是否存在負相關。需要指出的是:該命題的描述對象為城市1、城市2構成的整個經濟系統,而非單獨的城市1或城市2,從式(23)也可以直接看出這種區別。 下面,本文將比較市級數據、省(區)級數據以及國家級數據,并從中選擇最合適的數據。其中,市級數據相當于地級市內各縣、縣級市為城市1,市轄區為城市2;省級數據相當于省(區)內一部分城市為城市1,另一部分城市為城市2;國家級數據相當于全國一部分城市為城市1,另一部分城市為城市2。雖然在理論上國家級數據最為理想,但因其截面個體只有一個,故本文果斷放棄。對于市級數據和省級數據,本文認為省級數據較為理想,其原因:一是,市級數據有“虛假面板”現象。根據第六次人口普查數據,2010年全國總人口13.33億人,城市人口4.04億人,城市人戶分離人口1.70億人。在城市人戶分離人口中,有1.33億人,其中省內跨市轄區為0.75億人,跨省為0.58億人,共占城市人口的32.95%。若使用市級數據,則32.95%的跨市轄區人戶分離意味著“虛假面板”現象,也就是說即使有城市、年份兩個維度的數據,但人口的跨城市大量流動,將導致城市個體發生變動,已經威脅到面板使用條件。當然,如果研究對象是城市的公共物品、住房等,則對面板使用條件的影響較小。二是,市級數據有效變量的可得性低。目前,市級數據主要從《中國城市統計年鑒》《中國區域經濟統計年鑒》、各省(區、市)統計年鑒、全國人口普查中搜集。其中,《中國城市統計年鑒》數據以市轄區數據居多,這很難滿足理論命題對研究對象的要求;《中國區域經濟統計年鑒》數據以全市數據居多,但可用的指標較少;各省(區、市)統計年鑒數據參差不齊,口徑不一致;全國人口普查中關于人口的數據較全,但經濟類的數據幾乎沒有,且時間序列太少。總而言之,既要保證樣本量不能太少,又要保證個體間的相互作用不能太高,同時還要保證數據可得性不能太低,最終本文選擇了省級數據。當然,對于省(區、市)際的相互影響(比如人口流動等),在技術層面上,本文是通過空間計量解決的[注]但空間面板模型一般要求為平衡面板,這意味著:若某省在某年的某個變量為缺失值,則要么剔除該省,要么刪除該年,要么剔除該變量尋找替代變量。由于省際關系至少為省的二次關系,故刪省的方法應謹慎;又由于數據所支撐的時間跨度本身就不大,故刪時間的方法也應謹慎;而尋找替代變量的代價相對較小,故本文采之。另外,由于本文理論模型側重于分析個體內部的均衡,所以個體間的相互作用不應過大(而市際關系明顯過大),否則會喧賓奪主,即使空間計量在一定程度上可以解決此類問題。。 本文所用的省級數據主要來源于國家統計局,部分缺失數據由各省統計年鑒、Wind資訊數據庫、中國經濟與社會發展統計數據庫、中經網統計數據庫補充。接下來本文將選擇合適的被解釋變量、關鍵解釋變量及控制變量,如無特殊說明,本文中所有的價格變量均利用CPI進行調整,基期為2010年。 被解釋變量。被解釋變量為綜合人力資本,本文用human_capital表示。參考郭劍雄(2005)、鄧峰和丁小浩(2012)、李海崢等(2013)等文獻,本文選取了教育人力資本、科研人力資本來計算綜合人力資本。又因為身體越健康意味著抗病能力越強、可承受勞動強度越高(Fogel,1994a,1994b),故本文還加入了健康人力資本(王弟海,2012)。也就是,綜合人力資本由科研人力資本(強調成果)、教育人力資本(強調智力)、健康人力資本(強調體力)三部分構成。綜合人力資本計算,主要包括成本法(Kendrick,1976)、收入法(Jorgenson and Pachon,1983;Jorgenson and Fraumeni, 1992a,1992b)和特征法(Barro and Lee,1996)等,本文主要采用特征法,其計算公式為:綜合人力資本=科研人力資本s×教育人力資本s×健康人力資本s。其中,s取1(正向指標時)或-1(負向指標時);科研人力資本用人均發明專利申請量來推算,教育人力資本用受教育年限來推算,健康人力資本用修正死亡指標[注]需要說明的是,修正死亡指標是一個負向指標,由于死亡人數還包括因年邁而造成的自然死亡,故本文利用“死亡人數/65歲及以上人數”來削弱這種影響。來推算。圖2為2005—2014年中國31個省份的綜合人力資本圖,可以發現:北京、天津、上海、江蘇的綜合人力資本較高;同時,北京的綜合人力資本增速最快,這主要源于北京對周邊省份過強的虹吸效應。 圖2 2005—2014年中國31個省(區、市)綜合人力資本 關鍵解釋變量。由于關鍵解釋變量為運輸成本,出于計量模型穩健性的考慮,本文選擇了多個代理變量。需要注意的是,本文理論模型中的運輸成本是指“運輸單價×運輸線路長度”,故計量模型的代理變量也必須圍繞“運輸單價×運輸線路長度”。在計量主模型中,本文選用了總運輸成本占比freight_total作代理變量,其計算公式為:總運輸成本占比=交通運輸、倉儲和郵政業/GDP*100,該變量更側重于“運輸單價×運輸線路長度×運輸重量”。而在計量穩健性檢驗中,本文試圖采用相對運輸單價、公路密度、人口密度作代理變量。對于相對運輸單價freight_price,其推算過程為:先利用“交通和通信的居民消費價格指數/CPI”計算得到交通和通訊的相對指數,再以2010年為基期,通過連乘(除)計算即可,該變量更側重于“運輸單價”。對于公路密度density_road,其計算公式為:公路密度=公路線路里程/行政區域土地面積,選擇該變量是因為公路密度越大意味著最優運輸線路越短,越不易出現繞行,該變量側重于“運輸線路長度”。對于人口密度density_pop,其計算公式為:人口密度=年末人口數/行政區域土地面積,選擇該變量是因為人口密度越大意味著運輸起點和運輸終點的直線距離越短,而直線距離越短則意味著運輸線路越短,該變量也側重于“運輸線路長度”。考慮到人口密度往往還具有“運輸線路長度”之外的更多含義,故人口密度不直接替換主模型中的代理變量,而是與freight_total一起加入計量穩健性檢驗模型。 控制變量。①本科專科畢業生比uni_col。在數據處理層面,本科專科比所需數據主要包括:本(專)科招生數、本(專)科在校生數、本(專)科畢業生數、受教育程度為本(專)科的抽樣人數。由于新入學學生和在校學生幾乎不參與社會生產,故將這兩類數據棄之。又由于在計算被解釋變量綜合人力資本時,已經利用了受教育程度抽樣人數數據,若解釋變量仍利用該數據,則等同于人為構造了計量模型的顯著性,故也將該類數據棄之;通過排除法,本文認為畢業生數據更為合適。在變量選取層面,本科專科畢業生比要優于本科專科畢業生數,其原因為:一部分本科專科畢業生會選擇離開原就讀城市[注]當然,其他城市的本科專科畢業生也會選擇進入該城市。,導致剩余的本科專科人數發生較大變動,而本科專科畢業生比,則相對較為穩定。②人均病床數hospital_bed。人均病床數越多,意味著醫療硬件越完善,進而保障該地區居民的健康處在較高水準。③一般工業固體廢物waster。一般工業固體廢物有兩種處理方法,一種是“一般工業固體廢物產生量/年末總人口”,另一種是“一般工業固體廢物產生量/行政區域土地面積”。前者強調一般工業固體廢物的分配,后者強調一般工業固體廢物的外部性。很明顯,一般工業固體廢物是公共物品,并對附近所有人均具有負外部性,故“一般工業固體廢物產生量/行政區域土地面積”的處理方法更為合理。又考慮到環境庫茲涅茨曲線理論,故本文還引入了waste的二次項[注]由于在實際計量回歸時,本文對waster進行了對數化處理,故其二次項指的是對數化后的二次項。因為先取二次方再對數化,將會出現多重共線性。。④性別失衡single。其計算公式為:性別失衡=abs(15及以上男女人數差)/min(15及以上女性人數,15及以上男性人數)*100。“洞房花燭夜”是中國的四大喜事[注]“久旱逢甘雨,他鄉遇故知,洞房花燭夜,金榜題名時。”之一,再加上《中華人民共和國婚姻法》規定的一夫一妻制,所以較高的性別失衡意味著更多的人會被動單身(這里不考慮同性戀情況)。由于單身者將花費更多的時間和精力去追求異性,進而擠占了本應提升人力資本的時間精力,故本文初步判斷性別失衡與人力資本負相關。 表1匯總了本文所用變量的基本信息,可以發現:不同變量的數據相差較為懸殊,且被解釋變量的中位數不到其均值的四分之一。為了便于解釋變量的橫向對比(彈性關系),同時也為了提高被解釋變量的數據質量,本文對(除百分比變量freight_total 、uni_col、single以外)變量進行了對數化處理。圖3為對數化處理后的變量密度圖,可以發現:經過對數化處理后,被解釋變量的對稱性有所提高,其分布更接近于正態分布。 表1 變量統計 圖3 變量密度圖(以柱狀圖逼近) 本文回歸所用數據為2005—2014年中國省級數據,鑒于省際空間相互作用,本文的實證模型為空間面板(Spatial Panel)計量模型。 對于空間權重矩陣(Spatial Weighting Matrix),本文分別計算了三種空間權重矩陣[注]在實際計量回歸中,本文還對權重矩陣進行了行標準化處理。:第一種是基于省邊境是否接壤的二值權重矩陣;第二種是基于各省省政府經緯度的距離倒數權重矩陣;第三種是基于跨省人口流動的綜合權重矩陣,計算數據來源于第六次人口普查,該矩陣非主對角元素ij的計算公式為:元素ij=(2005年在j省居住而2010年在i居住的人口×2005年在i省居住而2010年在j居住的人口) /(2010年在i省居住的總人口×2010年在j省居住的總人口)。下面,本文將對空間權重矩陣進行篩選。 ①二值權重矩陣和距離倒數權重矩陣。二值權重矩陣僅考慮了鄰居省的相互影響,對鄰居的鄰居等二階以上空間滯后信息利用較少,故距離倒數權重矩陣更優。②距離倒數權重矩陣和綜合權重矩陣。距離倒數權重矩陣只考慮了(大部分)地理空間滯后信息,忽略了地形、方言、經濟、人口等信息。比如,西藏與新疆(接壤)的省會距離明顯小于西藏與河南,但由于昆侖山的阻擋反而不如西藏與河南的關系密切;上海與山東的距離明顯小于上海與北京的距離,但北京與上海的關系更為密切(在經濟、交通等方面)。而綜合權重矩陣則不同,它涵蓋了空間距離、地形、方言、經濟、人口、文化等全方位信息,其原因為:每個決策者在選擇具體流入的省時[注]當然,也包括繼續留在本省。,必然要考慮空間距離、地形、方言(李秦和孟嶺生,2014;劉毓蕓等,2015)、經濟、人口、文化等因素。最終,可以篩選出最優的空間權重矩陣——綜合權重矩陣,該矩陣是在被解釋變量為人的屬性變量時最為突出。 本文使用的空間計量模型為SARAR,具體如下: yt=ρWyt+Xtβ+Ztγ+u+εt (25) 其中,εt=λMεt+vt,vt~N(0,σ2I),向量yt為被解釋變量,矩陣Xt為關鍵解釋變量,矩陣Zt為控制變量,矩陣W、M分別為被解釋變量、誤差項的權重矩陣(本文假設W=M),向量u為個體固定效應。若變量有下標t,則表示該變量隨時間而變。該模型既考慮了被解釋變量的空間自回歸(SAC),又考慮了誤差項的空間自相關(SEM)。當ρ和λ均不為零時,模型為SARAR;當ρ不為零而λ為零時,模型退化為SAC;當ρ為零而λ不為零時,模型退化為SEM;當ρ和λ均不為零時,模型退化為普通面板模型。當然,在后面的穩健性檢驗中,本文還考慮了更為復雜的WSARAR。 表2給出了最終計量回歸結果。其中,標號A為只有控制變量的回歸結果,標號B為加入了關鍵解釋變量的回歸結果,Main列為解釋變量的回歸系數,Direct列為直接效應,Indirect列為間接效應。 表2 SARAR估計結果 注: 括號內為穩健標準差,***p<0.01,**p<0.05, *p<0.1。 觀察表2中的標號A情況,可以發現:所有控制變量對模型的解釋都非常顯著(p-value均小于0.01),且ρ和λ均顯著不為零,也就是被解釋變量空間自回歸,誤差項空間自相關。具體而言:uni_col系數顯著為正,說明本科生相對專科生越多,其綜合人力資本越高(主要為科研、教育人力資本)。lnhospital_bed系數顯著為正,說明醫療硬件越完善,其綜合人力資本越高(主要為健康人力資本)。lnwaster和(lnwaster )2系數均顯著為正,說明綜合人力資本(主要為健康人力資本)隨一般工業固定廢物的增加呈現先減后增[注]注:lnwaster可以取到負數。的變化趨勢,這與環境庫茲涅茨曲線不謀而合。這是因為在經濟起步時期,人們一般不太關心環境污染,也不會過多處理污染物;但隨著經濟的進一步發展,人們開始注重自身健康,即使此時期污染物產生量有所增加,但是經過對污染物的有效處理后,其排放量反而有所下降。single系數顯著為負,說明性別失衡一定程度上造成了綜合人力資本的下降。 橫向對比表2中的標號A情況和標號B情況,不難發現:關鍵變量freight_total的加入,并沒有明顯改變原控制變量的符號和顯著性,也沒有使得ρ和λ變為不顯著;同時,R2也從0.7579提高到了0.7988。更為重要的是:freight_total的系數顯著為負(p-value為0.003),與理論模型中的命題完全一致。 本文的穩健性檢驗主要包括:增減關鍵解釋變量,替換關鍵解釋變量,替換估計方法。①增減關鍵解釋變量。對于減少關鍵解釋變量,在表2中,本文已將關鍵解釋變量減少為零個,回歸結果顯示所有控制變量及模型整體均較為穩健。對于增加關鍵解釋變量,本文謹慎選取了人口密度density_pop作為第二個關鍵解釋變量,由于該變量僅“部分”反映了運輸成本(側重運輸線路長度方面,人口密度越大暗示著運輸線路越短),故加入后不易造成多重共線性;回歸結果顯示(見表3的C列)所有解釋變量及模型整體均較為穩健,且lndensity_pop的系數顯著為正(p-value為0.068),符合本文理論模型命題。②替換關鍵解釋變量。本文分別用相對運輸價格freight_price、公路密度density_road對總運輸成本占比feight_tota進行替換,回歸結果顯示(分別見表3的D列、E列)所有解釋變量及模型整體均較為穩健,且lnfreight_price的系數顯著為負(p-value為0.076),lndensity_road的系數顯著為正(p-value為0.008),符合本文理論模型命題。 ③替換估計方法。考慮到本文的被解釋變量為人均變量,而不同省份又擁有不同的人口,故本文將對31個省(區、市)進行賦權。賦權原理為人口越多權重越大,具體操作為:先計算每個省2005—2014年的平均人口,再以該時間平均值作為這31個省(區、市)的頻率權重(Frequency Weights)。根據頻率權重,本文將估計模型升級為WSARAR,回歸結果顯示(見表3的F列)所有解釋變量及模型整體均較為穩健。 表3 穩健性檢驗結果 注: 括號內為穩健標準差,***p<0.01,**p<0.05,*p<0.1。 在Black and Henderson(1999)的工作基礎上,本文構建了適用范圍更廣的經濟增長模型,該模型基本涵蓋了產業理論、單中心城市理論、冰川運輸理論、公共財政理論。利用該模型,本文得出運輸成本一般會負向影響(穩態)人力資本的命題。在實證部分,利用中國31個省(區、市)面板數據,通過控制被解釋變量空間自回歸、誤差項空間自相關、個體固定效應等因素,得到運輸成本確實顯著地負向影響了(綜合)人力資本的結果,而通過增減關鍵解釋變量、替換關鍵解釋變量、替換估計方法等操作,回歸結果仍然保持了一定的穩健性。本文的研究不僅可以解釋京津冀和長三角的人力資本差別,還可以解釋為什么偏遠地區(運輸成本一般較高)的人力資本較低,沿海地區、平原地區(運輸成本一般較低)卻集聚了較高的人力資本。按照本文邏輯,即使偏遠地區出現了部分高人力資本群體,在該地區也是一種“浪費”,于是該地區的高人力資本群體將會向沿海地區、平原地區流動,即人才集聚。這種現象非常切合中國實際,每年都有很多本碩博畢業生,而大部分本碩博畢業生沒有選擇回家鄉,很可能是他們的人力資本在家鄉很難有用武之地。總之,根據本文研究,中國政府通過投資鐵路、公路、橋梁等基建而拉動經濟增長的做法是值得肯定的,尤其是西部大開發,這對于縮小人力資本地域差距起到了關鍵作用,而人力資本地域差異的縮小也將會一定程度上縮小工資的地域差異。 下面,對本文理論作進一步拓展。μ作為關鍵變量,被定義為運輸成本,主要是指空間領域,強調的是物質從一個空間轉移到另一個空間產生的“成本”,若將μ的概念拓展至時間領域,μ可以定義為人的非耐心程度,當人越沒有耐心時,人將會給予未來的物質更低的權重,也就是μ越大。單位時間的貼現因子和時間的長度均會影響人的耐心,當單位時間的貼現因子越小時,人們對未來物質的賦權越小;當時間越長時,人們對未來物質的賦權也越小。鑒于此,本文原理論所指的不同空間中的兩類城市(代表著上下游產業),可以轉化為不同時間下的前后生產工序(或上下游產業)。當人對時間越沒耐性或前后生產工序越耗時,物質的總貼現“價值”越低,也就是μ越大。若將μ的概念拓展至社會領域,μ可以定義為交易成本,主要是為了交換所有權而產生的“成本”。其中,所有權是指所有人依法對物質所享有的占有、使用、收益和處分的權利,而交易成本屬于(新)制度經濟學范疇,Coase(1937)、Williamson(1981)作了更多原創性工作。2.2 系統穩態分析



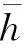
3 實證檢驗
3.1 數據選擇與討論


3.2 空間權重矩陣
3.3 空間計量回歸結果

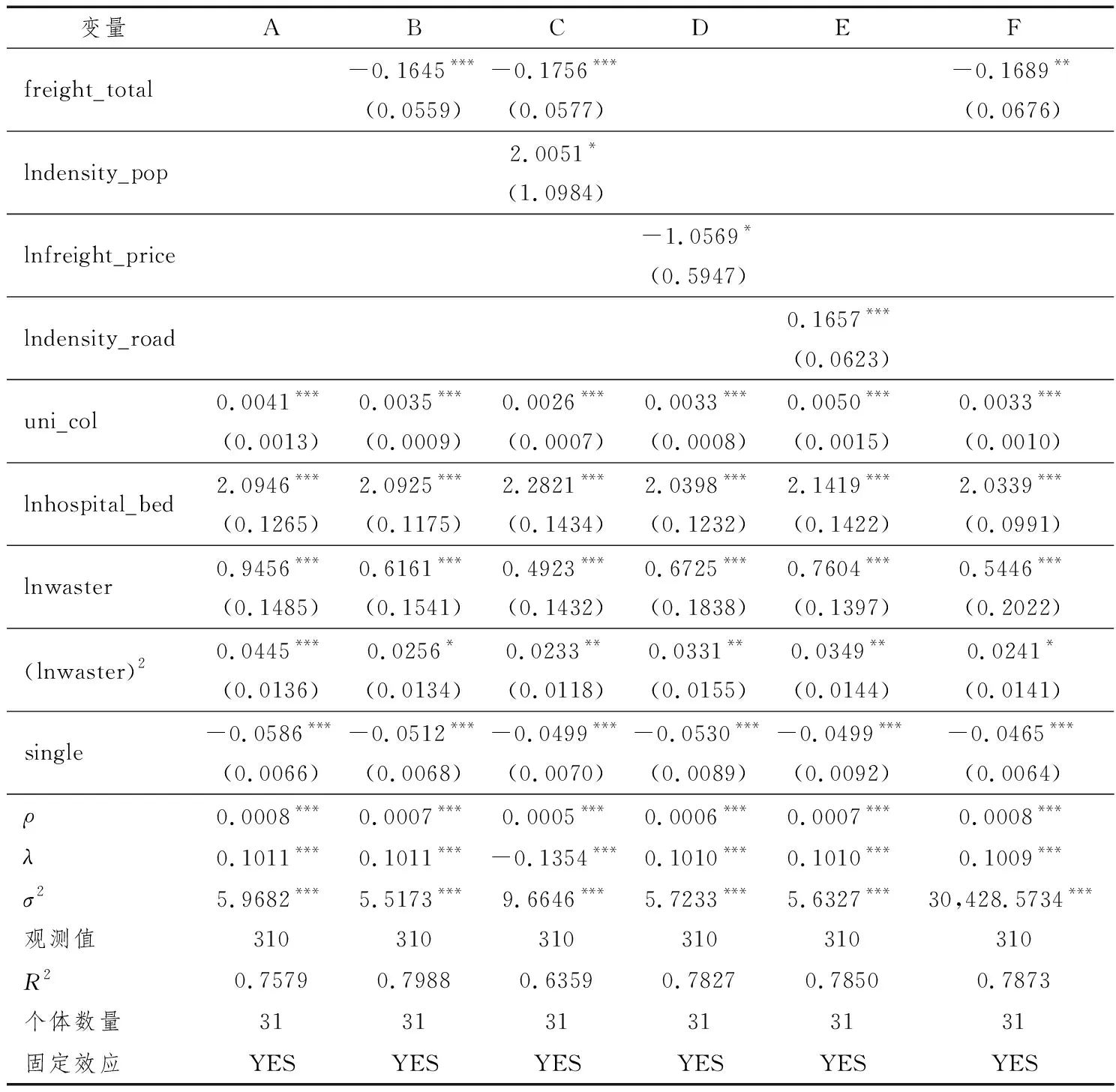
3.4 穩健性檢驗
4 結語與啟示

