基于TDOA/FDOA多星聯合定位誤差與衛星構型分析

秦耀璐 楊淑萍 束鋒,,3 孫琳琳 陸錦輝 許正文 桂林卿

(1.南京理工大學電子工程與光電技術學院,南京 210094; 2.中國電波傳播研究所 電波環境特性及模化技術重點實驗室,青島 266107; 3.東南大學 移動通信國家重點實驗室,南京 210096)

引 言

無源定位是指在不發射電磁波的條件下獲得目標的位置. 利用小衛星平臺,能進行大范圍的搜索和電子偵察,基于衛星的高精度無源定位技術在導航、跟蹤和電子對抗等軍事和民用領域有著廣泛的應用. 到達時間差(time difference of arrival, TDOA)定位技術利用由目標輻射源信號到達不同觀測站的時間差確定的多個雙曲面相交進行定位,到達頻率差(frequency difference of arrival, FDOA)定位技術則利用目標輻射源與觀測站相對運動產生的多普勒頻移差進行定位. 相較于其他無源定位技術,無源TDOA定位精度較高. 若目標輻射源與觀測站之間存在相對運動,利用FDOA信息可以進一步提高定位性能,TDOA/FDOA聯合定位能很大程度地提高定位精度,因此聯合定位技術有廣闊的應用前景[1]. Ho在文獻[2]中提出了利用TDOA/FDOA對運動目標進行定位的經典兩階加權的最小二乘(weighted least squares, WLS) 算法. 近年來,定位領域的國內外學者提出了許多利用TDOA和FDOA測量信息進行定位的算法[3-9]. 文獻[3]提出了基于加權代價函數的TDOA/FDOA聯合定位算法,避免了加權WLS算法存在的只能在一定的噪聲環境中使得定位誤差達到克拉美·羅界(Cramer-Rao lower bound, CRLB)的問題,使得定位對于噪聲的穩定性大幅提高. 文獻[4]提出了利用最大比合并技術基于最大似然原理的TDOA/FDOA定位算法,該算法的定位性能在有無地球約束的條件下均優于單獨定位性能,并且逼近CRLB,但最大比合并的聯合搜索定位算法實現復雜度較高. 文獻[5]提出了基于網格搜索的加權最大似然代價函數定位算法,該算法與最大比合并的定位性能近似相等,但在復雜度上,節省了一半左右的計算量. 由于最大似然估計問題的非凸性質,如果沒有良好的初步估計,難以獲得全局最優解,因此,文獻[6]將定位問題重新定義為加權最小二乘問題,將定位問題最終化成半正定松弛問題求解．TDOA/FDOA聯合定位方法通常不具有直接的解決方案,并且需要數值方法來確定發射器的位置,文獻[7]提出了解決非線性優化問題基于粒子群算法的TDOA/FDOA聯合定位方法. 文獻[8]研究了采用最陡下降法和最大似然估計法的分布式被動傳感網絡中移動目標源的TDOA/FDOA定位算法. 在最新的研究中,文獻[9]將目標位置估計問題轉化為二次約束二次優化問題,使用拉格朗日乘數法求得了近似解析解. TDOA/FDOA定位算法層出不窮,因而對評判定位算法性能的標準提出了迫切要求. 研究聯合定位的CRLB[10],可以衡量各種定位算法的性能優劣,分析影響定位精度的各種因素.

Ho和Chan于1997年推導了多星TDOA和FDOA聯合定位的誤差CRLB[11],由此確定了無偏估計器中最優無偏估計器所能達到的最好定位性能. 孫仲康在文獻[12]中推導了TDOA測量誤差較小情況下的多星TDOA定位方差. Pattison和Chou在文獻[13]中分析了雙星聯合定位的幾何精度因子(geometric dilution of precision, GDOP)和方差,發現TDOA定位曲面、FDOA定位曲面與地球表面夾角為90°時定位精度最好. 文獻[14]和文獻[15]對雙星聯合定位算法和誤差分析進行了更深入的研究. 由于Ho推導的聯合定位方差公式CRLB并不適合于TDOA/FDOA三星單獨定位,故文獻[16-17]討論了三星定位誤差分析. 文獻[18]分析了多星TDOA/FDOA聯合定位中時差誤差和頻差誤差對定位精度的影響. Ho等[2]于2007年在考慮接收機位置和速度存在測量誤差情況下,推導了運動目標多星聯合定位的方差下界,即CRLB,但是未能給出顯式表達式.

本文將應用Taylor級數、矩陣理論和統計理論等多種手段進行簡化處理獲得靜態目標的方差CRLB顯式表達式,有效地簡化定位精度分析. 同時考慮到三星單獨定位不能直接應用該式,我們將雙星的聯合定位誤差推導思路應用于三星單獨定位情況,并獲得其定位誤差公式. 進一步,本文分析和討論了多星衛星構型對定位性能的影響. 仿真結果表明,FDOA較容易產生定位盲區,且該盲區無法通過衛星構型設計來避免,而TDOA的定位盲區可以通過設計良好的衛星構型完全消除. 此外,TDOA/FDOA聯合定位時,能有效避免TDOA或FDOA帶來的定位盲區,且能顯著提高定位精度.

1 系統模型

三維空間的多星無源定位系統由M個衛星組成,位置向量為ri=(xi,yi,zi)T(i=1,2,…,M),未知目標源位置坐標向量為r=(x,y,z)T. 從未知目標源到衛星i的單位位置向量可表示為

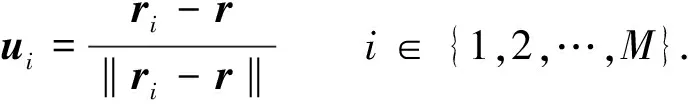
(1)

目標源到任何兩對衛星j和i的TDOA 和FDOA可表示為

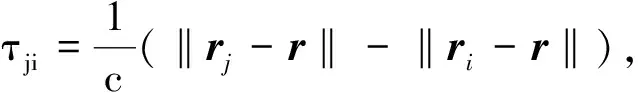
(2)

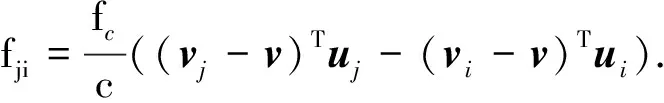
(3)

式中:c表示光速;fc為目標源載波頻率;vi和v分別為衛星i和目標源的運行速度. 考慮衛星位置誤差與速度誤差,對式(2)和式(3)進行Taylor展開,得到如下表達式:

Δτji=τji(r+Δr,ri+Δri,rj+Δrj)-τji(r,ri,rj)

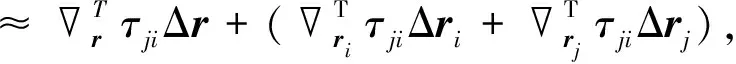
(4)

Δfji=fji(r+Δr,ri+Δri,rj+Δrj,vi+Δvi,

vj+Δvj)-fji(r,ri,rj,vi,vj)

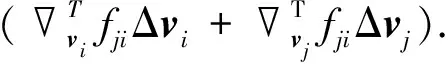
(5)

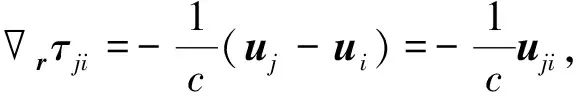
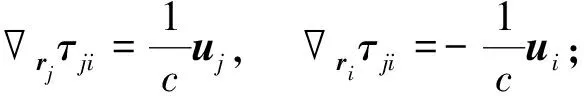
(6)

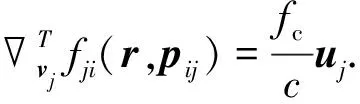
(7)

式中,βi和pij表示為

pij=ri-rj．

(8)

選擇衛星1為主星,收集所有的時差和頻差構成TDOA和FDOA向量,共有N=M-1個獨立時差和頻差對,即

Δτ=(Δτ21,Δτ31,…,ΔτM1)T,

Δf=(Δf21,Δf31,…,ΔfM1)T.

(9)

將時差向量和頻差向量合成大的向量,定義如下向量矩陣表達式

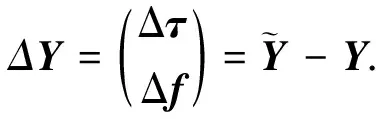
(10)

考慮TDOA和FDOA測量誤差、衛星自定位誤差,以及衛星速度測量誤差的影響,利用式(4)～(7),定位誤差方程可近似表示為向量矩陣形式

Y(r,rs+Δrs,vs+Δvs)-Y(r,rs,vs).

(11)

式中:r表示目標位置;rs+Δrs表示測量獲得的衛星位置,rs為衛星實際位置,Δrs為衛星位置測量誤差;vs+Δvs表示測量獲得衛星的速度向量,vs為衛星實際速度向量,Δvs為衛星速度向量測量誤差;而

Y(r,rs+Δrs,vs+Δvs)-Y(r,rs,vs)=Δrs+Δvs．

(12)

令

(13)

于是式(11)更改為

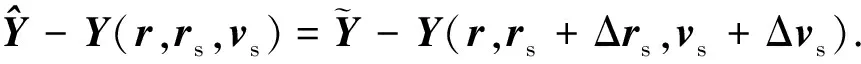
(14)

由式(14)有

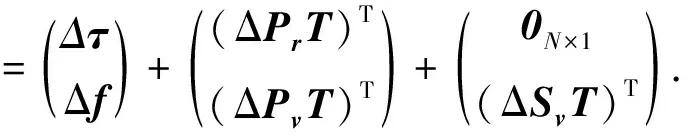
(15)

式中:左邊表示定位誤差;右邊第一項表示TDOA/FDOA測量誤差,第二項表示衛星自定位誤差,最后一項表示衛星速度測量誤差,均服從高斯分布．式(15)中各矩陣向量可表示如下:

T=(-e,IM-1)T.

(16)

式中:

Δri=Δr1+Δri1,i∈{2,3,…,M};

e=(1,1,…,1)T;

(17)

2 多星定位誤差分析

2.1 多星TDOA/FDOA聯合定位誤差

基于式(14)和(15)得到接收的時差頻差聯合向量概率密度如下[10]:

(18)

我們得到Fisher信息矩陣[10]

J=E{[lnp(Y;r)][lnp(Y;r)]T}

(19)

式中,

Gr=(Gτ,rGf,r),

(20)

Gτ,r與Gf,r均為3×N(N≥3)的矩陣．定義

u=(u1,u2,…,uM),β=(β1,β2,…,βM),

T=(-e,IM-1)T,

(21)

利用矩陣T,結合式(8)和式(21),得到:

(22)

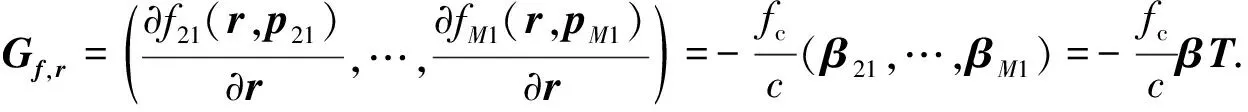
(23)

以及

Σ=E{ΔYΔYH}

(24)

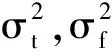
GDOP2(x,y,z) =tr{J-1}

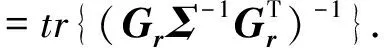
(25)

當考慮地球約束[11]時,

(26)

式中,re為地球半徑．則受地球約束的多星TDOA/FDOA聯合定位的GDOP為

GDOP2(x,y,z)=tr{J-1-J-1F(FTJ-1F)-1FTJ-1}.

(27)

式中,F=(2x,2y,2z)T. 上面推導的多星GDOP,也可稱為CRLB聯合公式,適用于四星及以上單獨定位系統和三星及以上聯合定位系統. 因此,我們將在下節推導考慮地球約束后的三星TDOA單獨定位誤差公式.

2.2 三星單獨定位誤差

上節推導的多星聯合公式不適用于三星單獨時差或頻差定位,主要原因是僅有兩個測量參數,導致Fisher信息矩陣為奇異矩陣,無法求逆. 本節將以TDOA為例,專門推導三星單獨TDOA定位的GDOP.

對于三星單獨定位,兩測量參數加上地球約束三個方程恰好可聯立求解目標的位置向量,其思路類似于雙星TDOA/FDOA. 類似于文獻[19],考慮衛星位置測量誤差后,如式(2) 所示的TDOA定位方程以及式(26)地球約束依據Taylor級數可展開為:

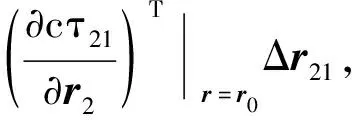
(28)

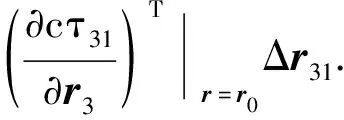
(29)

0=(2x,2y,2z)T|r=r0Δr

(30)

式中:Δr為定位目標的誤差項;Δr1為衛星1也就是主星的絕對測量誤差,Δri1為衛星i相對于主星的相對測量位置誤差,即Δri=Δr1+Δri1,i∈{2,3}. 為表達方便,下面推導中忽略r=r0. 將式(28)～(30)組合成矩陣向量形式,有

Δd=HΔr+H1Δr1+ΔH2．

(31)

式中:

H=(-u21,-u31,2r)T;

H1=(u2+u1,u3+u1,03)T;

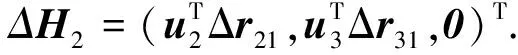
(32)

其中ui和uji見式(1)和式(6),03表示全零的三維列向量. 由式(31)得到

Δr=H-1(Δd-H1Δr1-ΔH2)．

(33)

根據GDOP的定義,我們有

GDOP2(x,y,z) =tr{E(ΔrΔrT)}

(34)

3 衛星構型設計討論

地球半徑re=6 378.137 km,以五星為例分析多星構型,圖1是五星的定位系統圖. 地心為O,其中主星為A,副星為B、C、D和E. 星下點定義為主星和地心的連線與地球表面的交點,星下點為S. 主星高程為h,假定目標位于P處,θ表示主星-副星連線與主星-星下點連線夾角.AB=AC=AD=AE為主副星之間的距離. 給定主星的位置,四顆副 星的經緯度坐標及高程隨θ變化而變化. 由于衛星間距一般在10 km到200 km之間變化,此值同衛星高程與地球半徑相比可忽略. 考慮到五星編隊飛行,于是五顆衛星速度向量可近似為相等.

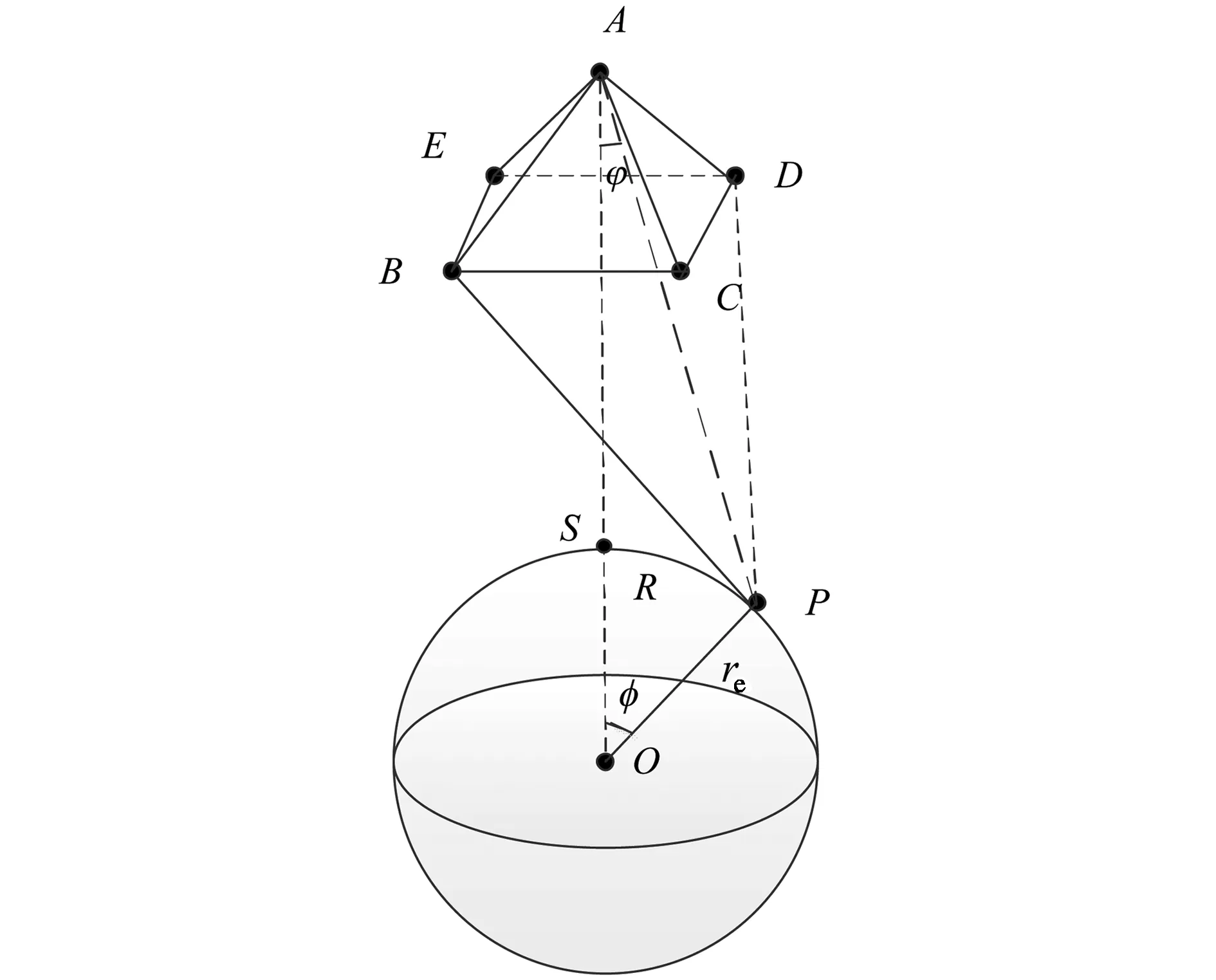
圖1 五星定位系統框圖Fig.1 Block diagram of five-satellite localization system

定理1 目標位于地球表面且距離星下點距離為Rkm范圍無定位盲區充分條件:主星-副星連線與主星-星下點連線夾角θ滿足φ<θ<180°-φ.

證明:

當目標P位于距離星下點Rkm圓周上時,對應的∠AOP為

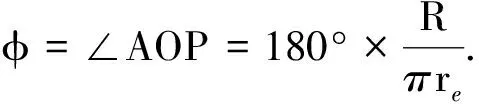
(35)

利用此角度可獲得線段AP長度等于

(36)

于是,可得∠PAO=φ如下:

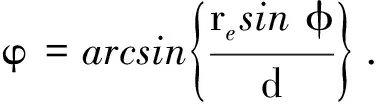
(37)

若φ>θ,顯而易見,在AC延長線與地球表面交點至P點一段存在定位盲區. 為了保證在星下點Rkm范圍內不出現定位盲區,令φ≤θ,考慮目標P距離星下點Rkm,且位于主星-副星連線AC的延長線與地球表面交點附近,此時φ=θ,即主星A、副星C、目標P在同一條直線上. 令主星A為衛星1,副星C為衛星3,由ui的定義式,且由于衛星間距變化與同衛星高程和地球半徑相比可忽略,得到u3=u1,即

u31=u3-u1=0．

(38)

僅考慮單獨TDOA定位時差測量誤差,式(25)簡化為

GDOP2(x,y,z) =tr{J-1}

(39)

(40)

根據Cauchy-Schwarz不等式可得

=9．

(41)

由式(41),有

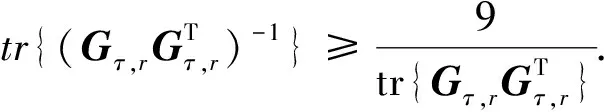
(42)

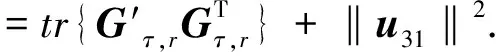
(43)

目標P位于主星-副星連線的延長線與地球表面的交點附近,利用式(38),得到‖u31‖2=0. 由式(43)可知,相較于其他區域,目標位于主星-副星連線的延長線與地球表面的交點附近時,定位性能下降,形成定位盲區.

同理,當θ>180°-φ,即θ+φ>180°,AE的反向延長線與地球表面的交點至目標P一段存在定位盲區.

令θ=180°-φ,即目標P位于AE的反向延長線與地球表面交點附近,可以得到,此時定位性能下降,該處形成定位盲區,證明同上.

綜上,為了保證在星下點Rkm范圍內不出現定位盲區,四顆副星與主星連線同主星到星下點連線的夾角θ必須滿足下面不等式:

φ<θ<180°-φ．

(44)

證畢.

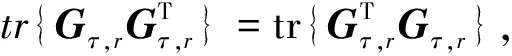
(45)

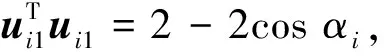
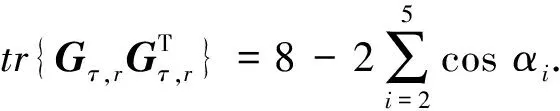
(46)

通過分析式(42)和(46)可知,增大αi可提高定位性能,當保持主副星之間的間距不變時,αi隨相鄰主星-副星連線間夾角βi的增大而增大. 如圖1所示具有良好對稱結構的衛星構形βi均為β,即∠BAC=∠BAE=∠CAD=∠DAC=β,利用余弦定理可得β與θ關系為

cosβ=cosθ2．

(47)

當θ=90°時,β取得最大值90°.因而主星-副星連線與主星-星下點連線夾角θ趨于90°時,則主星-目標連線與副星-目標連線的夾角αi越大,定位性能越好.

4 仿真分析

設置系統仿真參數如下:TDOA測量誤差為50 ns,FDOA測量誤差5 Hz. 采用五星定位系統,主星位于上方頂點,高程為h=1 000 km,東經130°,北緯0°,其他四顆副星位于主星下方構成正方形,主星到副星間距保持150 km不變,主星到其他四副星連線同主星到星下點連線夾角均為θ.

4.1 衛星構型對GDOP的影響

圖2、圖3和圖4分別繪出了θ=40°,θ=70°時,TDOA單獨定位的GDOP曲線、FDOA單獨定位的GDOP曲線以及TDOA/FDOA聯合定位的GDOP曲線.

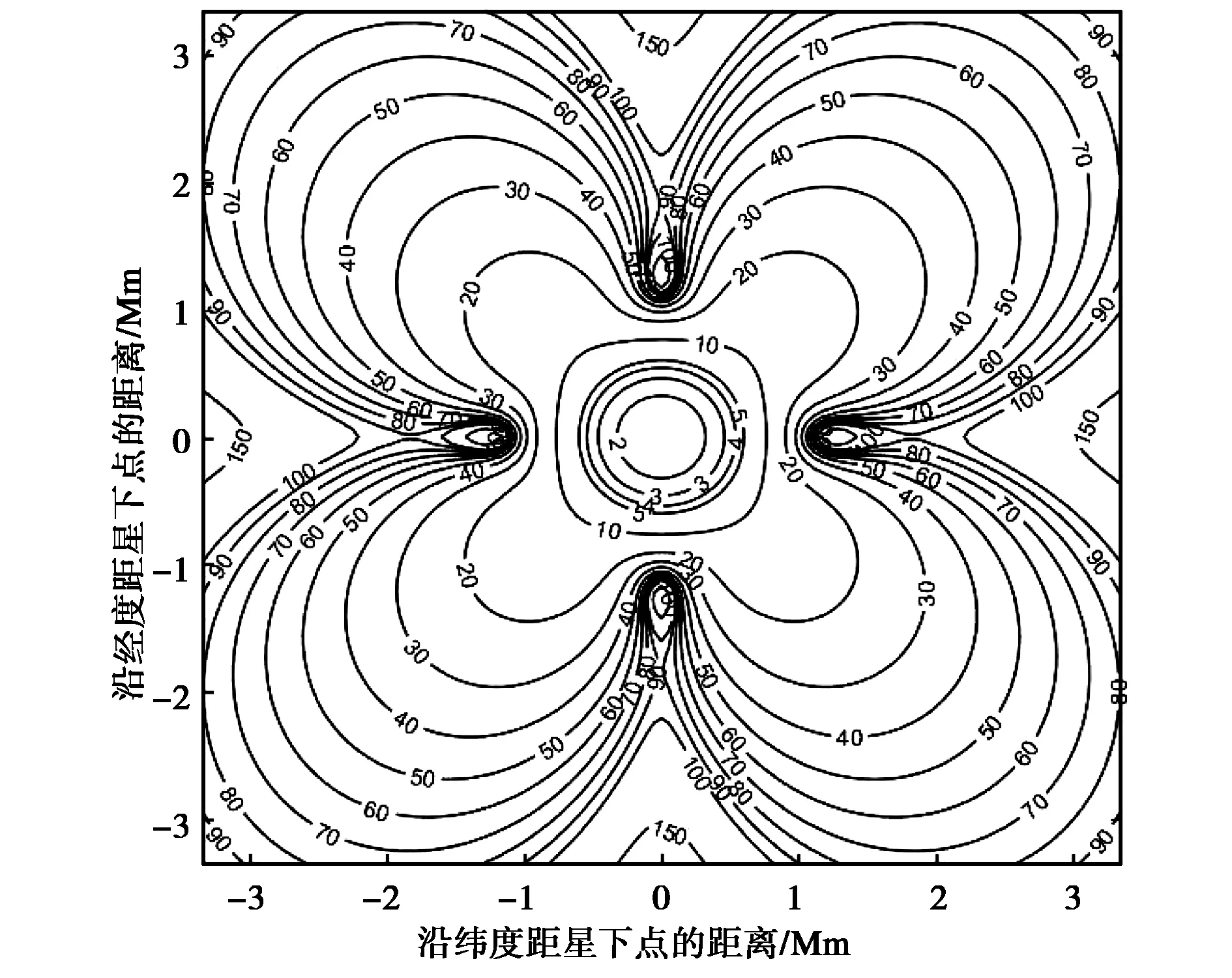
(a) θ=40°

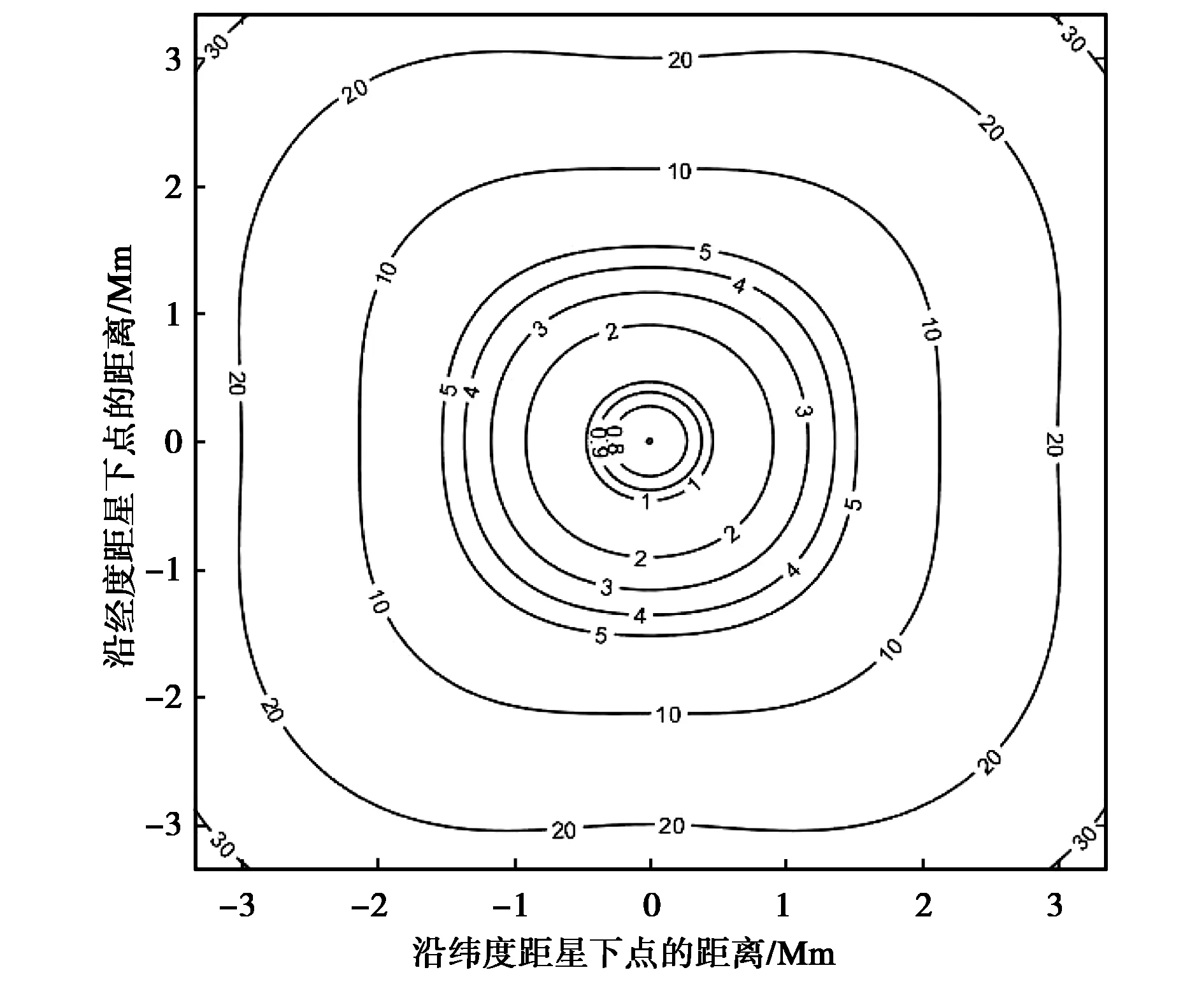
(b) θ=70°圖2 TDOA單獨定位的GDOP曲線Fig.2 GDOP of TDOA localization

(a) θ=40°

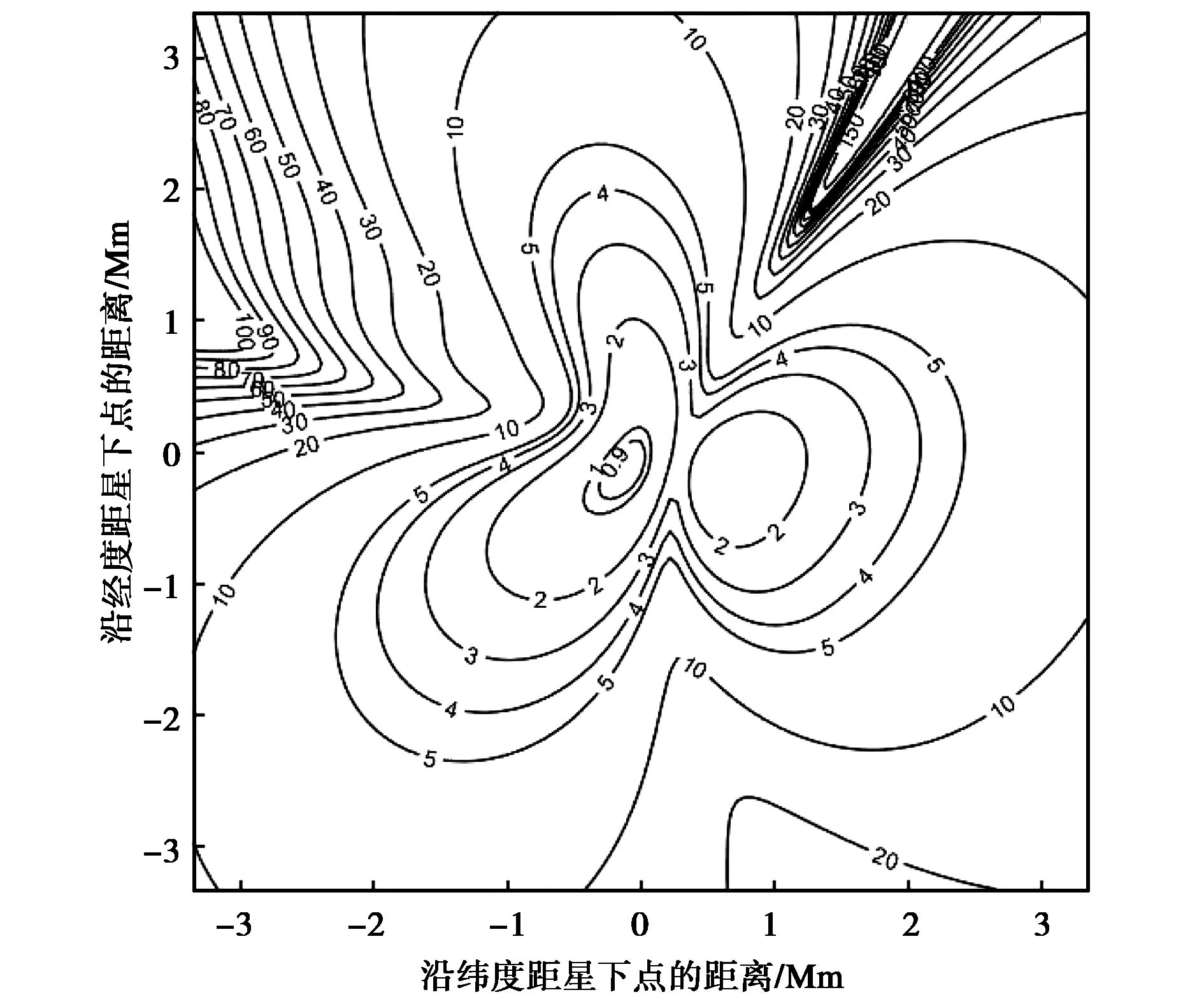
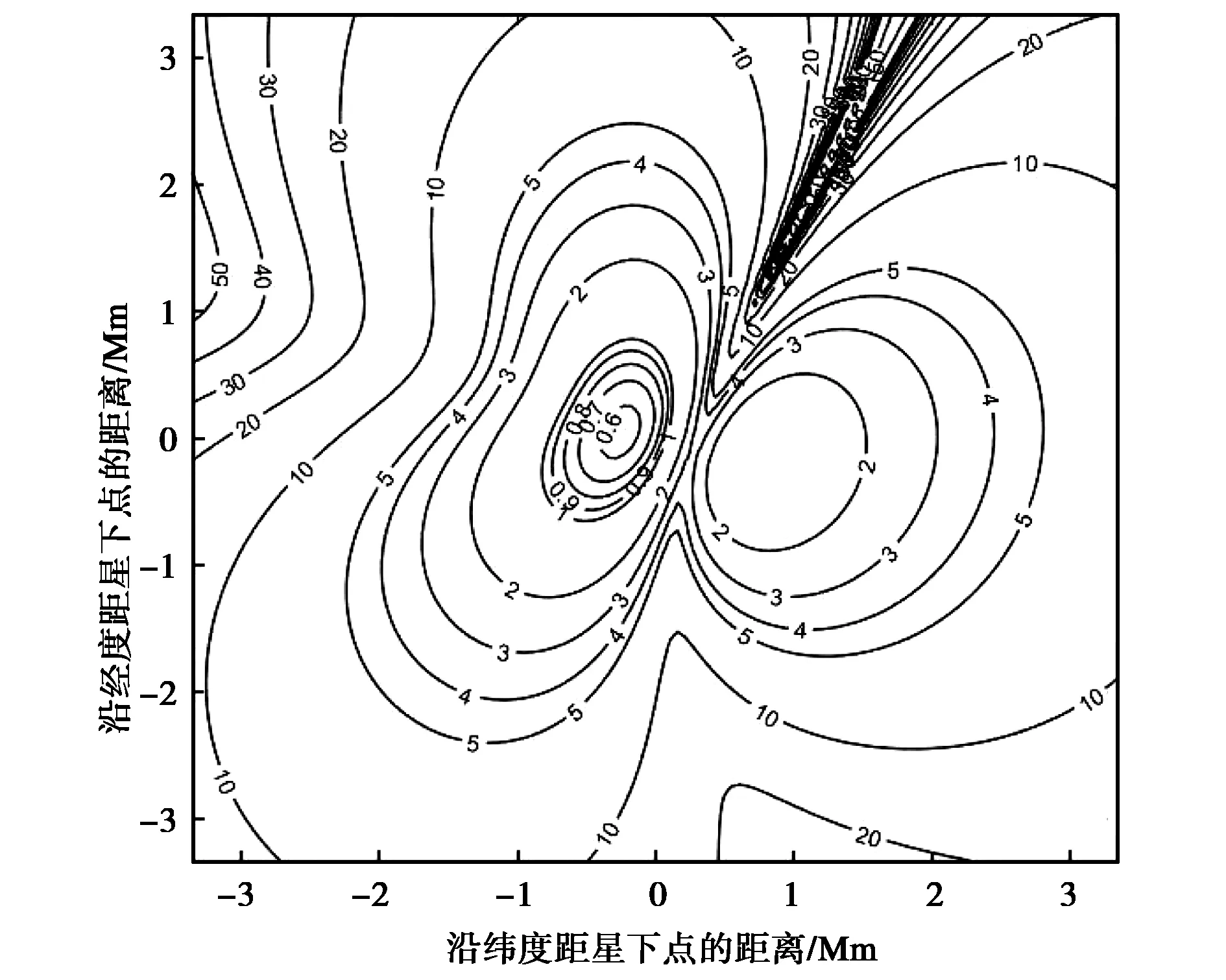
(b) θ=70°圖3 FDOA單獨定位的GDOP曲線Fig.3 GDOP of FDOA localization

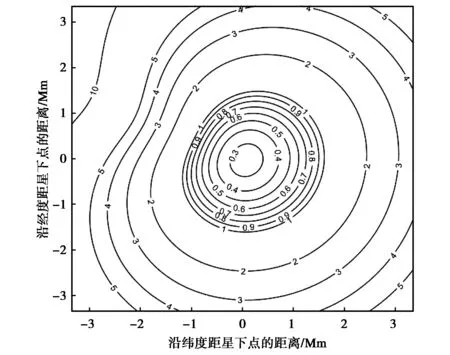
(a) θ=40°

(b) θ=70°圖4 TDOA/FDOA聯合定位的GDOP曲線Fig.4 GDOP of joint TDOA and FDOA localization

由圖2(a)可知,當θ=40°時,TDOA單獨定位存在四個定位盲區,它們由主星-副星連線與地球交點附近區域形成盲區. 在設計衛星構型時盡量保證所有主星-副星連線與地球不相交,則可避免這些定位盲區. 圖2(b)示出了θ=70°時定位盲區已經消除. 比較圖2(a)和圖2(b)發現TDOA在星下點的單獨定位精度由2 km提升到0.8 km,遠離星下點精度也有顯著提升,因此增加θ角可提高TDOA定位精度.

仔細觀察圖3會發現:有一條通過星下點的定位盲區,此盲區內FDOA的定位誤差較大．該盲區實際上是垂直于衛星速度方向通過主星的平面同地球相交圓周形成,由于衛星繞地球飛行,此平面與地球表面肯定相交,因此定位盲區是沒有地球約束FDOA定位系統本身所固有的. 產生物理機制如下:此圓周上任意一點到衛星連線近似垂直于衛星速度方向,因此速度在此連線上沒有分量,產生的Doppler頻率為零,不起任何作用,也就是不提供任何定位信息. 因此角度變化對FDOA定位盲區消除沒有影響.

結合圖4(a)和圖4(b)可知θ角度變化對聯合定位精度基本沒有影響．比較圖2、圖3和圖4可知,TDOA/FDOA聯合定位時,不存在定位盲區,且相較于TDOA單獨定位和FDOA單獨定位,定位精度明顯提高.

4.2 衛星位置誤差、衛星速度誤差對GDOP的影響

系統仿真參數設置如下:主星到其他四副星連線同主星到星下點連線夾角均為θ=70°.

圖5繪出了衛星位置絕對誤差和相對誤差為1 000 m、100 m,及100 m、10 m兩種情況下TDOA/FDOA聯合定位精度隨離星下點距離的變化曲線. 由圖5可知:當衛星位置絕對誤差為100 m,相對誤差為10 m時,衛星位置誤差對定位精度近乎沒有影響;在衛星位置絕對誤差為1 000 m,相對位置誤差為100 m時,衛星位置誤差較大,衛星位置對定位精度的影響已經凸顯,相較于衛星位置絕對誤差為100 m相對誤差為10 m,定位精度下降約1.2 km. 圖6繪出了衛星速度誤差分別為2 m/s,10 m/s時,TDOA/FDOA聯合定位精度隨離星下點距離的變化曲線. 由圖6可知,衛星速度誤差對定位精度影響較大. 相較于無衛星速度誤差的TDOA/FDOA聯合定位,對距星下點2 000 km左右的區域,衛星誤差為2 m/s時,定位精度下降約3 km;衛星誤差為10 m/s時,定位精度下降約6 km. 比較圖5與圖6可知,衛星位置誤差提升一個數量級,定位精度約下降1.2 km,而衛星速度誤差由2 m/s增大至10 m/s,定位精度平均下降約2.7 km. 速度測量精度對定位精度的影響較大,而測距精度對目標定位精度的影響較小. 圖7繪出了同時考慮衛星位置誤差和速度誤差,TDOA/FDOA聯合定位精度隨離星下點距離的變化曲線. 比較圖5和圖6可知,當衛星位置誤差較小時,速度誤差為影響定位精度的主要因素. 同時圖7示出綜合考慮位置誤差與速度誤差,當位置誤差達到一定量級時,衛星位置誤差將會使定位精度產生大幅度下降.

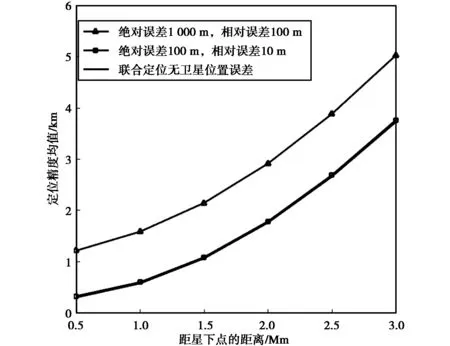
圖5 衛星位置測量誤差對定位精度的影響Fig.5 The effect of satellite position measurement errors on location accuracy

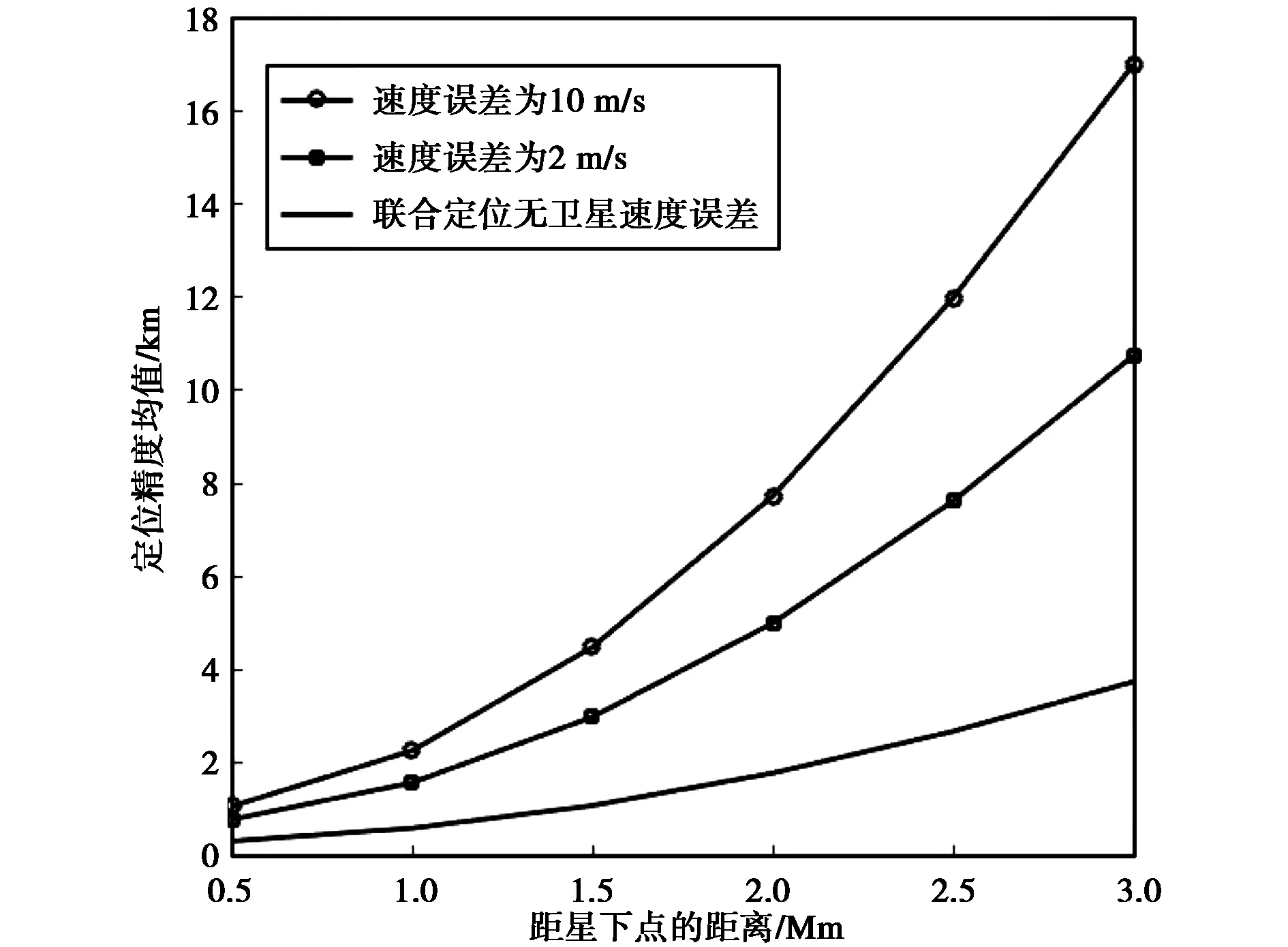
圖6 衛星速度測量誤差對定位精度的影響Fig.6 The effect of satellite velocity measurement errors on location accuracy

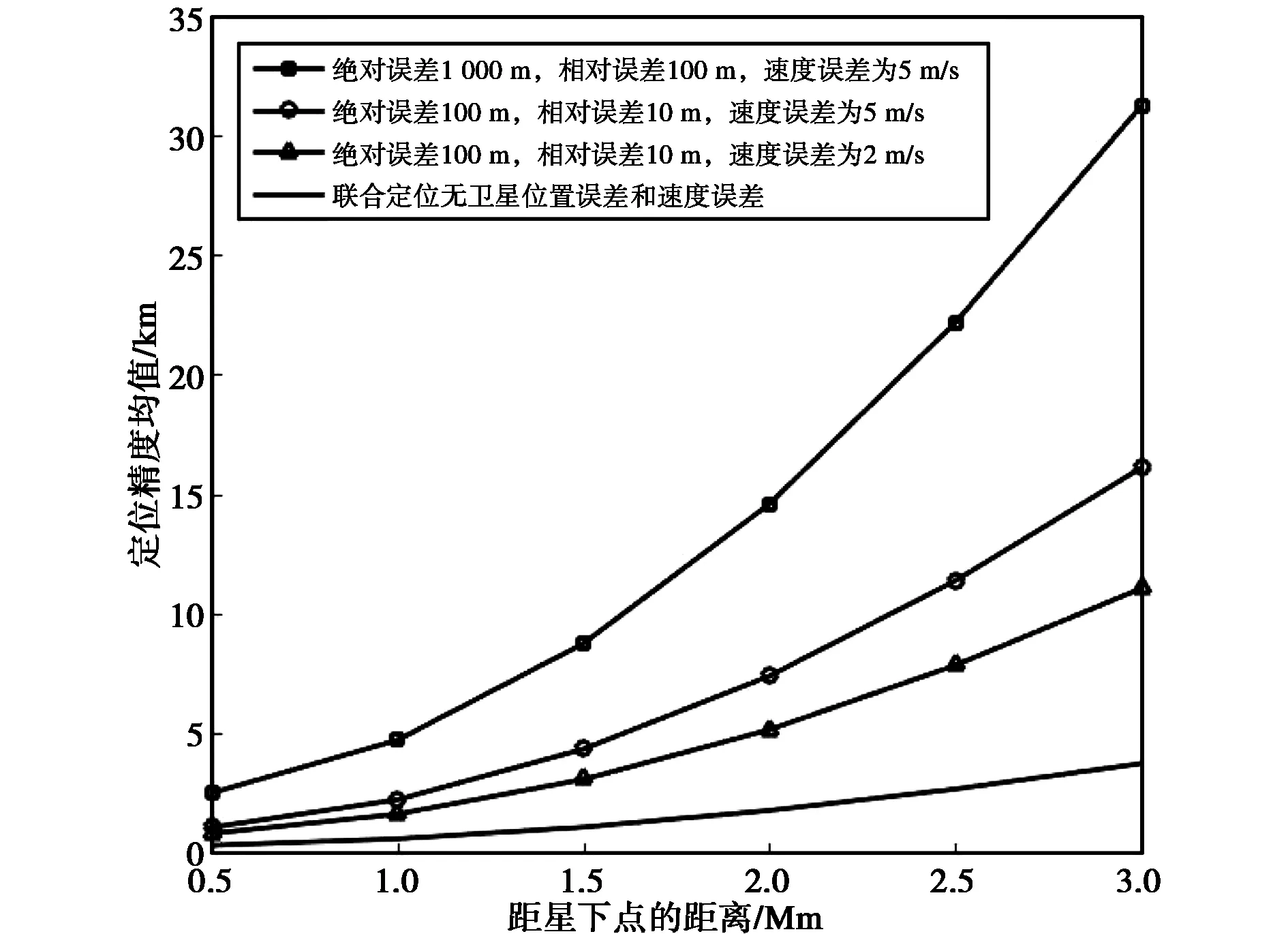
圖7 衛星位置和速度測量誤差對定位精度的影響Fig.7 The effect of satellite position measurement and velocity measurement errors on location accuracy

5 結 論

本文推導了多星TDOA/FDOA聯合定位的誤差公式,該公式充分考慮了TDOA測量誤差、FDOA測量誤差、衛星自定位誤差和速度測量誤差. 并且對衛星自定位誤差與速度誤差進行仿真分析,發現衛星速度誤差是影響定位精度的關鍵因素. 最后對衛星構型進行了簡單的討論. 由此可見,良好的衛星構形、高精度的衛星速度測量與TDOA/FDOA聯合定位相結合可以保證相當高的定位精度．