基于人工神經元網絡和多特征參數的預警震級估算

楊黎薇 林國良 邱志剛 江汶鄉 王玉石

摘要：預警震級測定是地震預警的關鍵技術環節之一。在滿足地震預警系統時效要求的前提下，以國內現有的人工神經元網絡構架為基礎，考慮采用更多的特征參數，對實時持續計算確定預警地震震級的方法進行研究。通過對日本部分實際強震數據進行持續估算預警震級與實際震級間的偏差情況，對預警震級和實際震級進行線性擬合，提出對預警震級結果的修正公式，進一步完善本方法快速估算預警震級的準確程度。

關鍵詞：地震預警；震級估算；人工神經元網絡；特征參數；線性擬臺

中圖分類號：P315.9 文獻標識碼：A 文章編號：1000-0666（2018）02-0302-09

0 引言

自然災害本身不可避免，但如果能預先采取一些合理的防御措施就可以有效地減少這些災害造成的損失。為了達到減輕地震災害的目的，除加強城市工程結構抗震設計外，人們最先想到的就是地震預報，但現有科技水平還無法徹底攻克這一難題，地震的預測預報必將長期處于探索和研究階段。地震預警是目前世界上公認的能夠有效減輕地震災害的新手段之一（金星等，2012；何少林，2017）。

實時震級計算是地震預警系統中最重要功能模塊之一，也是整個地震預警系統中最復雜、最困難的部分（張紅才，2013；楊黎薇等，2017）。預警震級對時效性要求很高，主要利用布設在潛在震源區周圍的實時傳輸地震觀測臺站，在破壞性地震發生后極短時限內，根據距離震中較近的若干個觸發臺站信息，迅速判斷地震規模，并采用這若干個觸發臺站數據估算震級，隨著觸發臺站數目不斷增多，以不停變更的信息量對震級最初測定結果進行修正，在規定時限內得到最終測定結果。

1 預警震級估算相關研究

目前，國際上也發展形成了一些實用的實時震級測定方法，所采用的參數雖然各不相同，但基本突破點主要建立在有效利用P波段攜帶地震信息這一基礎條件上。Nakamura（1988）最早提取P波段初始數秒內地震信息去評估地震震級大小。在此思路的影響下，地震學家通過對P波段以及s波段記錄的深入分析，以實測地震記錄為基礎，得到了一些比較成熟的地震預警震級測定方法。最常見的計算方法大致可分為周期（頻率）參數算法、幅值參數算法、能量參數算法以及其他算法。

1.1 周期（頻率）參數算法

大多數的地震預警系統使角的地震預警震級估算主要是以周期（頻率）參數為依據推演得到的。其代表方法有τpmax方法及τc方法。

τpmax方法主要利用實時速度記錄去計算地震動的卓越周期，τpmax值是從臺站觸發開始的若干時間內（通常為3 s）計算得到的卓越周期最大值。多年來，各國專家學者不斷對τpmax參數法進行改進，其中Shieh等（2008）所定義的τpmax公式得到廣泛認可：式中：α表示平滑參數，該值決定了平滑過程的速度，一般取值0.999；xi表示記錄中地面運動的速度時程；Xi表示平滑后地面運動的速度導數平方值；Di表示平滑后地面運動的加速度導數平方值。

Kanamori（2005）對τpmax改進后提出τc方法。其后，Shieh等（2008）對τc參數的計算方式進行詳細推導：式中：積分區間[0，t0]表示記錄中P波觸發后3s內的時間窗；u（t）是位移時程。τc方法的基本思路與τpmax方法是一脈相承的。τpmax通過步步積分獲取固定時間窗內周期參數；τc通過區間積分獲取固定時間窗內周期參數。

周期參數與震級之間并不是簡單的線性函數關系。τpmax參數是幅值和頻率的非線性函數，其準確性和穩定性受采樣率影響，且與記錄的預處理過程密切相關，采用不同濾波器或者不同長度時間窗，計算出的預警震級有明顯差異；而改進后的τc參數直接將時間窗長度設置為3s，對于6.5級以下的地震，基本可以根據τc參數算法做出準確的預警震級估算。從目前的研究現狀來看，使用周期參數估算預警震級對于中小震而言，估算結果是較為理想的。

1.2 幅值參數算法

幅值參數算法是為了有效利用地震P波初始數秒內的波段信息而引入了記錄波形峰值位移的幅值參數，其對位移幅值Pd參數的定義是初始P波3s時間窗內的垂直分量峰值位移。Wu等（2007）采用2階高通巴特沃斯濾波器（低頻截止頻率為0.075Hz）進行濾波，利用美國南加州地震記錄，選用撿拾到P波后3s時間窗內的位移幅值Pd的衰減關系去預側震級，以此為基礎，張紅才（2013）利用基本的震源理論推導出初始P、S波段的位移幅值Pd與最終震級間的關系，具體公式如下：式中：u（t）表示震中距為R處的P、S波位移場；const表示常數；R表示震中距；M表示地震矩速率；c表示地震波速；Δu表示斷層平均滑動速率；∑表示斷層中初始階段的滑動斷層面積；C表示一階幾何參數；L表示斷層線性尺度。

多數學者對幅值參數算法的穩定性及可靠性表示肯定，這種算法利用單個臺站觸發3s時間內的信息記錄就可得到相關參數，對臺網密度的要求有了極大的降低，張紅才（2013），金星等（2012）主要推薦絇Pd問ㄗ魑詰卣鷦ぞ？統中優先采用的方法。這種算法相對較簡便，節約時間，但對于M≥6.5的地震，其預警結果誤差較大。

1.3 能量參數算法

能量參數算法是從能量角度去考慮預警震級的測定方法，它充分利用了累計絕對速度（CAV）作為強地面運動的快速檢拾量，最初是用于伊斯坦布爾的早期地震預警系統，用來決定是否有破壞性地震正在發生。其定義式為：

CAV=∫0tmax|a（t）|dt（6）式中：積分下限0表示從臺站觸發開始計算，積分上限tmax可自行設定，即累計絕對速度（CAV）是通過對加速度積分計算得到的。該算法的基本思路是設定閾值，當給定臺站的CAV超過設定閾值時，第一觸發就會發生，有3個臺站超過設定閾值觸發時初始警報就會產生并對外宣布地震警報；初始警報過后，系統將自動更新設置一個更高的閾值，同樣，當3個臺站超過新設置的閾值時第二次警報繼續發布。能量參數主要是用于甄別地震是否具有破壞性，并不直接用于震級估算。

1.4 其他算法

Odaka等（2003）提出從單個地震記錄快速估算震中距與震級的新方法。為了定量分析不同的地震波形，采用Bt·exp（-At）這種簡單的函數形式，時間t從p波到達開始，通過對波形包絡線最初的部分進行最小二乘擬合，確定出擬合系數A，B，進而將A，B值作為快速估算震級大小的重要參數。用△表示震中距時，lgB與lgΔ成反比關系，這種關系適用于不同的地震震級，同時不受高頻噪聲的影響。

在震級、震源深度、震中距等因素影響下，地震波會在特定來源和觀測環境下形成各不相同的包絡波形，故本文考慮用1個直觀的形式去展現這些包絡波形。與后來P波與S波的最大振幅相比，初始P波最開始的振幅通常是非常小的，本文構建1個對數波形，先基線校正消除零點漂移或直流電（DC）組件的影響，再添加1個比標準噪聲偏差更小的振幅以免除零振幅現象。Odaka等（2003）使用Kyoshin-Net（K-Net）網上下載的強震動記錄，通過對數波形擬合，探尋初始地震波某部分（縱波到達后數秒內）不同的包絡系統在形式上對應的地震震級和震中距，進而確定出擬合系數A與B。具體操作如下：（1）繪出豎向加速度記錄包絡波形，確定P波到時：（2）取p波到時后3s內的包絡波形，擬合Bt·exp（-At）中A、B值，通常采用最小二乘法。

Odaka擬合系數法主要運用于日本UrEDAS系統，根據該系統的運行經驗，采用該方法也能夠快速準確獲取地震震級。可是參數B的取值需從大量的地震記錄中統計獲取，且參數B具有強烈的區域性，因而在我國實際應用并不廣泛。

綜上，實際的地震記錄是非常復雜的，地震震級的確定涉及到震源過程、傳播介質、場地條件、儀器性能等多個方面，并不是單一的周期參數、幅值參數或能量參數等就能準確穩定估算出來，這些參數只能在一定程度上反映地震的規模，不同參數估計得到的預警震級結果也可能存在著一些差異（林華偉等，2016）。因此，以國內較成熟的構建為基本，合理發展多種特征參數，也是非常值得研究的問題。本文以國內現有人工神經元網絡構架為基礎，除了選用常見的地震震級指示參數，考慮增加τpmax、τc、Pd、CAV以及記錄前半段擬合系數A、B等特征參數，對實時持續計算預警震級進行研究。通過實測擬定相應的預警震級修正公式，進一步完善快速估算預警震級的準確程度。

2 基于人工神經元網絡選取特征參數

本文的預警震級測定是在實測地震記錄基礎上，將地震p波段或者s波段的前幾秒記錄獲取特征參數與實際震級大小相聯系，得到預警震級測定的經驗擬合關系。由于不同特征參數之間屬于非線性關系，采用人工神經元網絡來確定預警震級。

2.1 選取人工神經元網絡

人腦神經元既有局部的計算和存儲功能，又可通過聯結構成統一體系。人工神經元網絡（簡稱ANN）是采用物理可實現的系統去模仿人腦神經細胞結構與功能的一種信息處理系統。ANN由大量簡單處理單元構成，具有巨量并行性、存儲分布性、高度非線性、結構變化性及自組協調性等特點（叢爽，2003）。它最大的特點是僅僅借助樣本數據，無需建立系統的數學模型，就可對系統實現由Rn空間（n為輸入節點數）到Rm空間（m為輸入節點數）的高度非線性映射。故而在結構分析中，可以直接使用人工神經網絡模型實現結構系統輸入參數與輸出參數之間的非線性映射，無需建立系統的數學模型（毛健等，2011）。圖1是最常見的人工神經元網絡結構模型，對輸入參數選取控制做了多項嘗試，并對一些在線計算非線性控制算法結果進行對比研究，其利用人工神經元網絡作為非線性過程模型，結合控制思想來組成控制器，在線尋找最優的ANN過程輸入參數，經過多種選擇比較，選擇出適合于控制思想的輸入量。

網絡信號只允許從較低層流向較高層，層號確定層的高低，層號較小者，層次較低；層號較大者，層次較高。本文采用了目前應用最廣泛的BP網絡，該網絡屬于3層網絡，涵蓋有輸入層、輸出層以及隱藏層，除輸入層和輸出層以外的其他各層都叫隱藏層。輸入層被記作第0層，負責接收來自網絡外部的信息；隱藏層不直接接受外界的信號，也不直接向外界發送信號；輸出層是網絡的最后一層，具有該網絡的最大層號，負責輸出網絡的計算結果。當信息向網絡輸入時，信息首先由輸入層傳遞至隱層節點，經特征函數作用后再傳至隱層，最終傳遞至輸出層進行輸出，期間節點的特性函數通常選用S型函數（叢爽，2003）。如圖2所示，本文以BP算法為基礎構架，隱藏層所采用的傳遞函數是tansig函數，輸出層傳遞函數設為線性函數。有數據觸發時，直接提取P波觸發3 s內所有的選取特征參數，從輸入層經傳遞函數到隱藏層，再經輸出層運算后確定震級估計值。

2.2 多特征參數選取

國內常用震級指示參數主要以周期和幅值兩方面的參數為主。從周期參數與震級的關系來看，P波的有效位移首脈沖累積寬度、P波位移脈沖有效上升時間以及峰值比Vmax/Amax與震級之間的擬合關系較好；而在幅值參數中，P波在某時間段內不同頻率的加速度峰值、速度峰值、位移峰值則直接影響著震級的結果（馬強，2008）。故而，本文在震級指示參數的基礎上，綜合考慮增加τpmax，τc，Pd，CAV，擬合系數A與B等與震級大小關系密切的特征參數，以此提高預警震級的準確程度。

圖3顯示了具體參數的選取，在綜合應用初始P波3s內的多個震級指示參數、有效特征參數，并采用人工神經元網絡中的ANN算法模型進行震級預測時，該網絡模型的實例輸入多參數分量，可連續估算出預警震級結果。

3 數據選取

以日本KiK-Net網（http：//www.kik.basai.go.jp/kik/）下載的強震動記錄為主，選取2011-2015年112個M5.0～7.0地震事件（記錄數據3500余條），震級統一使用M表示，挑選出波形記錄完整、不同震中距的臺站數據，將數據以震中距50km內、100km內以及大于100km分類，具體如圖4所示。

4 預警震級統計結果

連續估算預警震級需要設置合理時限，最早估算出的預警震級稱為最初預警震級，最后估算出的預警震級稱為最終預警震級。以圖4統計震例為主，選取主要特征參數進行人工神經網絡強震預警震級估算，通過預警震級與實際震級間的偏差統計，尋求預警震級與實際震級間的擬合關系。

4.1 內陸地震中預警震級與實際震級間的差異

為了探尋內陸地震與海底地震間預警震級的差異，本文將分別進行統計分析，將2者結果展開討論。

圖5主要展現了預警震級與實際震級間偏差變化趨勢，在該震級區間內，2者偏差以正數為主，即預警震級估算值比實際震級發震值大。圖5a中每1個數據點均代表了1個地震事件最初預警震級偏離實際震級的結果，震級相同但發震不同的地震，預警結果也各不相同。隨著實際震級逐漸增大，最初預警震級與實際震級間偏離程度逐漸減小。圖5b中每1個數據點均代表了1個地震事件最終預警震級偏離實際震級的結果，隨著實際震級逐漸增大，最終預警震級與實際震級的偏離程度也逐漸減小。可以看出圖5a中數據的離散程度大于圖5b。為了尋求兩者實質區別，本文計算了M5.0～6.0地震事件的預警震級與實際震級的平均偏差，如表1所示。

由表1可見，實際震級為M5.0時，預警震級與實際震級的平均偏差最大，基本接近0.8；隨著實際震級逐漸增長至M6.0，預警震級與實際震級的平均偏差越來越小，基本接近0.1。僅從表1可看出，最初預警震級與最終預警震級間差別非常小。

綜上，最終預警震級的偏差相對更小，故而選擇最終預警震級作為最后的預警震級結果，對其結果進行線性擬合，得到：

Mwarn-Mpra=-0.81649Mpra+4.91948（7）

Mwarn=0.18351Mpra+4.91948（8）式中：Mwarn表示預警震級；Mpra表示實際震級，下同。

由此，對于內陸地區的強震預警，我們可嘗試先以主要特征參數進行人工神經網絡強震預警震級估算，再結合公式（8）對預警震級進行修正。

4.2 海底地震中預警震級與實際震級間的差異

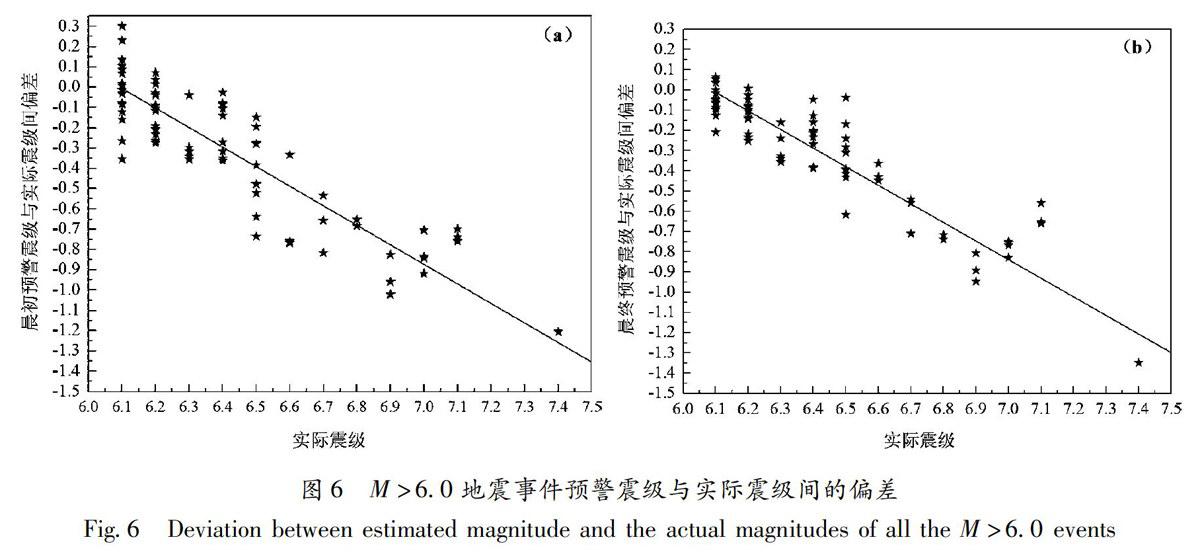
圖6為M>6.0地震事件的預警震級與實際震級間的偏差變化，與圖5的變化趨勢基本一致，但由圖6可看出，在該震級區間內，預警震級與實際震級間的偏差以負數為主，即預警震級估算值比實際震級發震值小。比較圖6a和6b，兩者的離散程度相差不大，偏差程度隨著震級增大而逐漸增大（偏差值為負數）。

表3的計算結果顯示，實際震級為M6.1時，預警震級與實際震級的平均偏差為0，屬于最佳理想結果；隨著實際震級逐漸增大，預警震級與實際震級的平均偏差越來越大，最大偏差值超過了-2.8。僅從表3可看出，最初預警震級與最終預警震級間差別接近于0。

表4主要計算了M>6.0地震的預警震級與實際震級的平均標準偏差。表4結果中有一個明顯劃分，M6.0～7.0地震的最終預警震級與實際震級的平均標準差小于最初預警震級與實際震級的平均標準差，對比單獨使用τc法和Pd法有明顯改善；M>7.0地震的，最終預警震級與實際震級的平均標準差大于最初預警震級與實際震級的平均標準差。

綜上，當實際震級M>7.0地震，預警震級基本無效。本文對M6.0～7.0地震的最終預警震級結果進行線性擬合，得到：

Mwarn-Mpra=-0.91899MPa+5.5943（9）

即：Mwarn=0.081011Mpra+5.5943（10）

由此，對于海底地區的強震預警，我們可嘗試先以主要特征參數進行人工神經網絡強震預警震級估算，再結合公式（10）對預警震級進行修正。

5.3 不同震級下預警震級與實際震級間的差異

將所有M5.0～7.0地震事件的預警結果與實際結果進行對比，如圖7所示，可看出M6.0地震事件預警震級與實際震級基本吻合。M<6.0地震事件預警震級大于實際震級；M>6.0地震事件預警震級小于實際震級（圖7a）。取每一個震級所有事件預警結果的平均偏差值，其平均偏差隨著實際震級增大呈線性變化（圖7b）。

對所有破壞性地震的預警結果進行線性擬合，在M5.0～7.0地震的預警震級與實際震級間的關系為：

Mwarn-Mpra=-0.84268Mpra+4.95758（11）

即：Mwarn=0.17532Mpra+4.95758（12）

公式（12）可用于所有破壞性地震的預警震級修正，其準確程度還需以國內大量地震數據進行下一步的驗證。

6 討論與結論

地震預警關鍵是首報的準確度，首報越準，越能保證地震預警的實際效益。本文在總結借鑒前人預警震級方法的基礎上，引入國際上成熟的特征參數τpmax，τc，Pd，CAV以及地震記錄前半段擬合系數A，B，利用2011-2015年日本KiK-Net網112余組M5.0～7.0地震事件（記錄數據3500余條），提出1套基于人工神經網絡和多種特征參數的預警震級估算法。通過持續估算預警震級與實際震級間的偏差，對預警震級和實際震級進行線性擬合，擬定對預警震級結果的修正公式，進一步完善快速估算預警震級的準確程度。

通過對研究結果的統計分析，得到如下結論：

（1）實際的地震記錄是非常復雜的，單一的周期參數或者幅值參數估算預警震級時，其離散程度與估算結果準確性息息相關。采用人工神經網絡方法持續對震級進行預測，應先檢驗選取的特征參數與地震震級間相關性是否緊密，即能否解決實質問題。本方法估算出的預警震級結果，其準確程度總體依賴前期工作中測試樣本的可信性，故前期的訓練極其關鍵。

（2）內陸地震震級多數為M7.0以內，以內陸地震為主的地震事件，預警震級的估算值通常比實際震級發震值大，可采用公式（8）進行相應的修正。海底地震震級多數在M7.0以上，以海底地震為主的地震事件，預警震級的估算值通常比實際震級發震值小，可采用公式（10）進行相應的修正。對所有M5.0～7.0破壞性地震而言，預警震級的估算值均可采用公式（12）進行相應修正。

（3）最后，本文所得到的結論與統計結果均是建立在日本臺網地震事件的基礎上，是否適用于中國地區還需更多國內的地震事件進行檢驗，有針對性完善并改進本文所提出的方法。

綜上所述，本文所提出的預警震級估算法，以人工神經網絡為基礎，綜合多個特征參數快速計算預警震級，并擬定了不同破壞性地震發生時可對應采用的修正公式，提高了預警系統震級信息的準確性，為地震預警系統建設提供一定的技術支持。

參考文獻：

叢爽.2003.面向MATLAR工具箱的神經網絡理論與應用[M].北京：中國科學技術出版社.

何少林.2017.地震烈度速度與預警臺站選址相關問題探討[J].地震研究，40（1）：15-21.

金星，張紅才，李軍，等.2012.地震預警震級確定方法研究[J].地震學報，34（5）：593-610.

林華偉，邱勇，劉超，等.2016.聯合卓越周期的震級預測新方法[J].價值工程，29：226-227.

馬強，2008.地震預警技術研究及應用[D].哈爾濱：中國地震局工程力學研究所，80-122.

毛健，趙紅東，姚倩倩.2011.人工神經網絡的發展及應用[J].電子設計工程，19（24）：62-65.

吳逸民，2006.如何利用地震初達波從事地震預警[J].自然科學簡訊，18（1）：8-11.

楊黎薇，邱志剛，林國良.2017.強震預警中P波到時STA/LTA和貝葉斯RIC雙步驟檢拾研究[J].地震研究.40（4）：629-637.

張紅才.2013.地震預警系統關鍵技術研究[D].哈爾濱：中國地震局工程力學研究所，43-70.

Kanamori H..2005，Real-Time Seismology and Earthquake DamageMitigation[J].Annual Review of Earth and Planetary Sciences，33：195-214.

Nakamura Y.1988.On the urgent earthquake detection am.system[C].Proceedings of Ninth World Conference on Earthquake Engineering.Ⅶ：673-678.

Odaka T，Ashiya k，Tsukadas，S，et al.2003.A New Method of Quickly Es-timating Epicentral Distance andMagnitude from a Single SeismicRecord[J].Bulletin of the Seismological SOciely of America，93（1）：526-532

Shieh，T，Wu Y M，Allen R M.2008.A comparison ofτc andτp mar formagnitude estimation in earthquake early warning[J].GeophysicalResearch Letters，35（20）：1-5.

Wu Y M，Kanamori H，Richard M A，et al 2007，Determination of earth-qaake early warning parameters，τc and Pd，for southern California[J]，Geophys J Int，170：711-717.