基于CA-Markov模型與ANUDEM內插法的崩崗侵蝕量預估

季 翔，黃炎和，林金石，蔣芳市，余明明，李紹鑫

?

基于CA-Markov模型與ANUDEM內插法的崩崗侵蝕量預估

季 翔1,2，黃炎和1※，林金石1，蔣芳市1，余明明1，李紹鑫1

（1. 福建農林大學資源與環境學院，福州 350002；2. 福建省土壤環境健康與調控重點實驗室，福州 350002）

崩崗是中國南方最為嚴重的土壤侵蝕類型之一，產生的大量泥沙危害農業生產和生態環境，因此對其侵蝕量的預估是防治該現象的重要途徑。崩崗面積較小且侵蝕劇烈，難以應用現有方法預估侵蝕量。該文應用CA-Markov模型和ANUDEM內插法對其高程級別模擬和空間內插，從而實現對崩崗侵蝕量的預估，并以福建省安溪縣龍門鎮的一處崩崗為例進行實證研究。結果表明：CA-Markov模型適用于對崩崗高程級別的模擬；ANUDEM內插法對崩崗地形的整體還原度較好，但對細節的刻畫不夠；以經過級別劃分和內插處理的高程數據為基期底圖計算得的崩崗侵蝕量較符合實際值，且實際侵蝕量越大，模擬精度越高；案例崩崗在一般年景、干旱年景和多雨年景中的年侵蝕量分別為：824.69、731.03和 924.57 m3，不同年景之間侵蝕量的最大差值為193.54 m3，因此在修建崩崗攔沙壩時需考慮不同降雨年景中侵蝕量的差異。研究結果不僅提供了預估崩崗侵蝕量的新思路，還可為崩崗侵蝕的防治工作提供參考依據。

侵蝕；模型；崩崗；侵蝕量；CA-Markov；ANUDEM

0 引 言

崩崗是指在水力和重力的作用下，山坡土石體受破壞而崩塌和受沖刷的侵蝕現象，主要集中在中國南方花崗巖發育的紅壤丘陵區。根據相關研究[1-3]，南方紅壤丘陵區共有各類崩崗239 125個，總侵蝕面積為1 220.05 km2，主要集中在江西、廣東、湖南、福建、湖北、安徽、廣西七省（自治區）。崩崗侵蝕產生的泥沙量巨大，不僅造成表土流失無法利用，而且泥沙被帶到下游埋沒農田、淤積河道水庫，給農業生產、生態環境以及人民生活帶來極大危害[4-5]。因此，預測和估算崩崗侵蝕量對減緩危害以及防治水土流失有重要作用。

土壤侵蝕量的估算方法眾多，主要是根據通用土壤侵蝕方程（universal soil loss equation, USLE）計算土壤侵蝕模數[6-7]或通過流域模型估算土壤侵蝕量[8-9]。然而由于崩崗相對其他類型的土壤侵蝕空間尺度較小，且侵蝕劇烈地表變化迅猛[10-11]，因此較難應用該方法預估崩崗的侵蝕量。崩崗的侵蝕量可由其地形體積的變化表示[12-13]，如劉希林等曾利用3D激光掃描儀對廣東五華縣蓮塘崗崩崗的演化過程進行空間監測，獲得了精確的崩崗侵蝕 量[13]。因此，可通過對崩崗空間的動態模擬計算其地形變化體積，從而實現對崩崗侵蝕量的預估。由于崩崗侵蝕過程的復雜性限制了機理型模型的應用[14-17]，經驗型模型更為適合。目前應用普遍的空間模擬模型是由馬爾科夫鏈（Markov）和元胞自動機（Cellular automatic，CA）耦合的CA-Markov模型[18-20]。該模型適用于離散的類型數據，對于連續變量需要進行級別劃分[21-22]。因此，應用該模型對崩崗地形變化進行模擬得到的結果為離散的高程級別，難以實現對崩崗侵蝕量的精確預估。

高程級別是將一定區間的高程值劃分為一個級別，相鄰級別邊界線上的高程取值相同，這與等高線類似。因此，可通過空間內插將離散的高程級別轉化成連續的高程數據，由此實現對崩崗侵蝕量的估算。空間內插法是一種將空間離散數據連續化的工具，在空間數據方面的應用較為成熟[23-25]，其中ANUDEM法在高程內插中的精度較高，應用成熟[24]。崩崗地表溝壑橫生，若單純根據等高線進行空間內插，難以體現地表細節。ANUDEM不僅可將等高線內插為精度較高的DEM數據，并且該方法可以根據地表徑流、湖泊等輔助信息強化地表細節，較為適用于對崩崗高程的空間內插。

本研究按照“連續-離散-連續”的思路，將連續的崩崗高程進行級別劃分使之適用于CA-Markov模型，并將預測得的崩崗高程級別進行ANUDEM空間內插，得到連續的崩崗高程預測值。通過與基期高程疊加得到土體體積變化量，從而實現對崩崗侵蝕量的估算。研究結果不僅提供了預估崩崗侵蝕量的新思路，還可為有針對性地防治崩崗侵蝕、減少河流泥沙提供參考依據。

1 研究方法

1.1 CA-Markov模型

1.1.1 Markov鏈

Markov鏈是基于Markov過程理論而形成的預測事件發生概率的一種方法，常用于具有無后效性特征地理事件的預測。一定區域內，不同空間類型具有相互轉化的可能，各類型之間的轉化過程有一些難以用函數關系準確描述的事件。在崩崗侵蝕過程中不同高程級別對應Markov過程中的“可能狀態”，而不同高程級別間相互轉換的面積數量或比例即為狀態轉移概率，可以利用如下公式對各高程級別的變化進行預測：

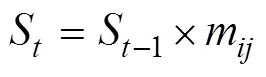
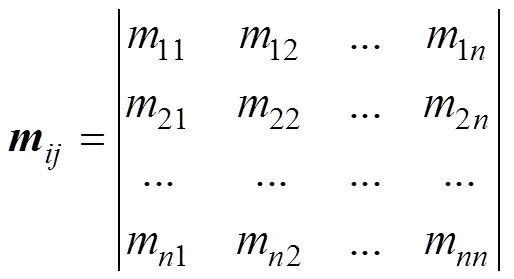
式中S1和S分別表示前一時刻和后一時刻的高程級別；m表示級高程轉變為級高程的概率，%，且各行之和為1；為高程級別的數目。

m是由前后兩期數據疊加而得，由于兩期數據時間間隔難以控制，因此需要將轉移概率進行轉換，使其符合預測的時間長度，這在模擬相對勻速的空間變化時效果較好[20]。然而，崩崗侵蝕劇烈且在時間尺度上差異較大[26-27]，若采用時間長度對其轉移概率進行轉換，難以反映崩崗侵蝕特征，模擬結果精度不高。崩崗是受水力和重力共同作用的復合侵蝕，水力作用主要來自于降雨后的地表徑流沖刷，重力作用同樣由于降雨增加土體重力導致，由此可知降雨量對崩崗侵蝕起著決定性的作用[28-30]。因此，本研究采用降雨量對其轉移概率進行轉換，公式如下：

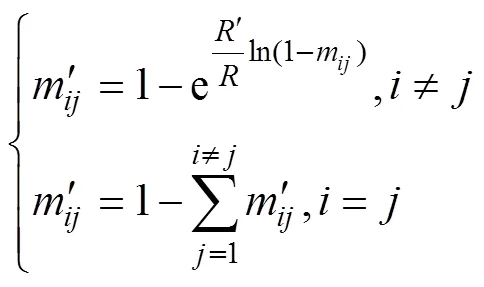
根據轉移概率矩陣可以計算得下一時刻每種類型的面積，從而對CA的空間分配進行數量約束。

1.1.2 CA-Markov耦合模型

CA模型是一個空間分配的自動機制，其對變量沒有要求，可以是離散數據也可以是連續數據，在土壤侵蝕方面得到過較多應用。該方法是通過將柵格圖中每柵格視為一個元胞，每個柵格值即為元胞狀態，根據轉換規則計算元胞的下一個狀態。CA-Markov模型是將Markov鏈的經驗性與CA的空間分配結合起來，以崩崗的地形級別為基礎數據，具體參數設置如下：

1）元胞：元胞大小即為柵格圖像大小，本研究設定柵格大小為0.1 m×0.1 m。

2）元胞狀態：在標準CA模型中，元胞狀態為一個有限的離散集合。因此在對崩崗地形的模擬中，需要將連續的高程數據進行級別劃分，高程級別即為元胞狀態。

3）鄰域：元胞的下一個狀態由元胞自身及其鄰域決定，需要計算鄰域對該元胞狀態轉變的影響。由于崩崗高程為連續型變化，因此本研究采用元胞到目標狀態最近距離表征鄰域影響，距離越小則鄰域影響越大，計算公式為：

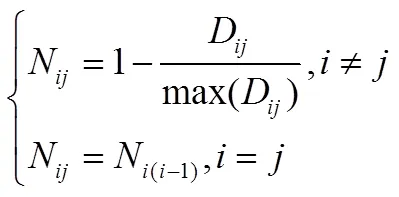
式中N為某個級元胞轉變為級的鄰域影響；D為該級元胞到級的最近直線距離，m；將所有級元胞的到級最近直線距離組成集合，集合的最大值為max(D)，由此可將N的取值轉化為0~1區間內。由于崩崗侵蝕的趨勢為高程下降，越接近下一級別，越難保持不變，因此保持高程級別不變的鄰域影響為到下一級別高程的 逆值。

4）適宜性圖集：適宜性和鄰域影響共同控制元胞狀態的轉變，由影響元胞轉變的驅動因素計算而得，計算公式如下：

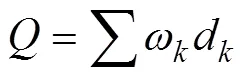
式中為適宜性，d和ω分別為第個驅動因素取值與該驅動因素的權重。

如前所述，崩崗受降雨后的地表徑流沖刷和重力的雙重作用。其中，崩崗的地表徑流即為溝道，重力則主要作用在坡度陡峭的土體上[29-32]。因此，本研究選擇溝道距離和坡度為表征崩崗侵蝕力的驅動因素。其中，降雨為崩崗侵蝕的關鍵驅動力，其作用遠大與土體自身的重力[30-32]，結合前期研究將這兩個驅動因素的權重設為0.75和0.25。

5）轉換規則：轉換規則是元胞自動機模型的核心，決定了元胞分配的動態過程。按照每個元胞的鄰域影響與適宜性之和，從最高值開始賦值，然后次高，直到滿足預測的數量。

1.2 ANUDEM內插

ANUDEM在對高程點或等高線的內插過程中，加入了如懸崖、河流等其他地形細節的數據作為約束，使內插后地形結構連續且地形細節準確，因此通過此方法能夠構建出體現水文地貌關系的DEM[20]。該方法的輸入數據包括基礎數據和約束數據兩部分。其中，基礎數據為：等高線、高程點；約束數據為：洼地點、地表徑流、湖泊、懸崖、海岸、邊界以及不需要計算的區域。

崩崗的高程級別為面狀數據，因此在進行ANUDEM時需要將其轉換為線文件，然后根據高程級別的分級值對各邊界線賦值，從而得到等高線數據，即ANUDEM內插的基礎數據。例如，級高程同時與-1級和+1級相鄰，將和-1級共用的邊界線賦值為級和-1的分級值，將和+1級共用的邊界線賦值為級和+1的分級值。崩崗侵蝕區的溝道對其土壤侵蝕以及崩崗地貌改變起著關鍵性作用，并且其空間位置較為穩定。因此，選擇溝道（地表徑流）作為應用ANUDEM對崩崗高程空間內插的約束數據。

1.3 崩崗侵蝕量

土壤侵蝕量可以通過質量或體積表示，考慮到在計算質量時，對土壤容重的選擇會產生誤差。因而，本研究采用崩崗的體積變化對崩崗侵蝕量進行表征，通過高程的柵格數據計算，公式如下：

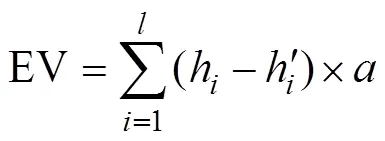
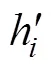
1.4 降雨情景設置

降雨量對崩崗侵蝕起著決定性的作用，因此本研究在構建模擬崩崗高程級別變化的CA-Markov模型時，根據降雨量對轉移概率矩陣進行轉換。然而，降雨是一種具有不確定性的自然現象，以現有數據難以準確預測未來的降雨量。情景分析法是對未來可能出現情況的分析及預測。因此，本研究采用情景分析法，根據研究區域的歷史降雨數據設置降雨情景，預測不同降雨情景下 崩崗地形的變化，從而估算出不同降雨情景時崩崗的侵蝕量。

2 結果與分析

2.1 案例點及數據

2.1.1 案例點選取

本研究的案例點位于福建省泉州市安溪縣龍門鎮（24°57￠N, 118°3￠E），該區域為亞熱帶季風氣候，年均氣溫為19 ℃，降雨量高且集中，年降雨量1 546.2～2 023.8 mm，且多在5—9月。該崩崗面積較大，約5 300 m2，雖然曾被橫斷修路治理過，但由于該崩崗侵蝕劇烈，道路已無法辨別。因此本研究以此崩崗為案例點，如圖1。

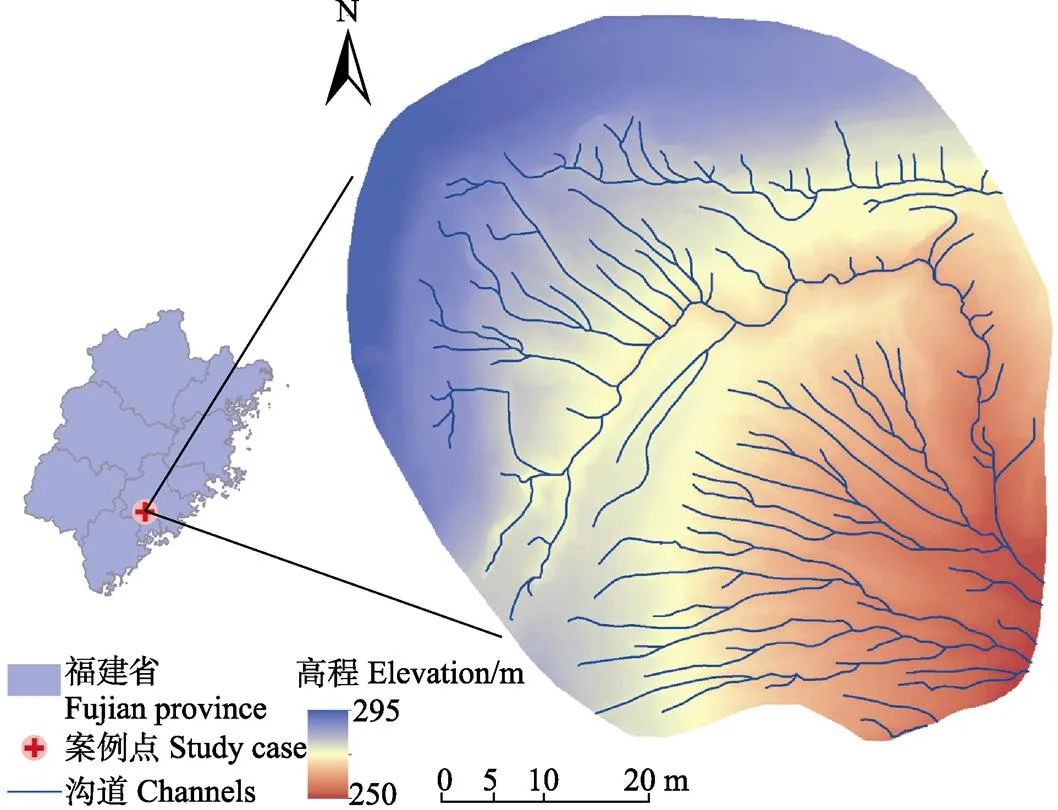
圖1 案例崩崗示意圖

2.1.2 數據來源與處理

1）高程及高程級別

分別于2017年3月11日、2017年7月21日和2017年12月2日，由RTK（Trimble R4 GNSS）設置控制點，無人機飛行器（DJI GO 4 APP）對案例崩崗進行低空攝影測量。經過拼接校正等處理，得到3個時期案例崩崗的DEM，其空間分布率為2.8 cm，投影坐標系為WGS-1984- UTM-zone-50N。過高的空間分布率將增加模型運行負擔，因此本研究對3期DEM進行了重采樣處理將其空間分辨率降為10 cm。

本研究中需要將連續的崩崗高程數據劃分級別。一般來說，級別劃分的越詳細，模擬結果越準確，但數目過多會造成模型運行負擔。因此，根據數據特征并結合現有研究成果[32]，將案例崩崗進行了高程級別的劃分，如圖2。

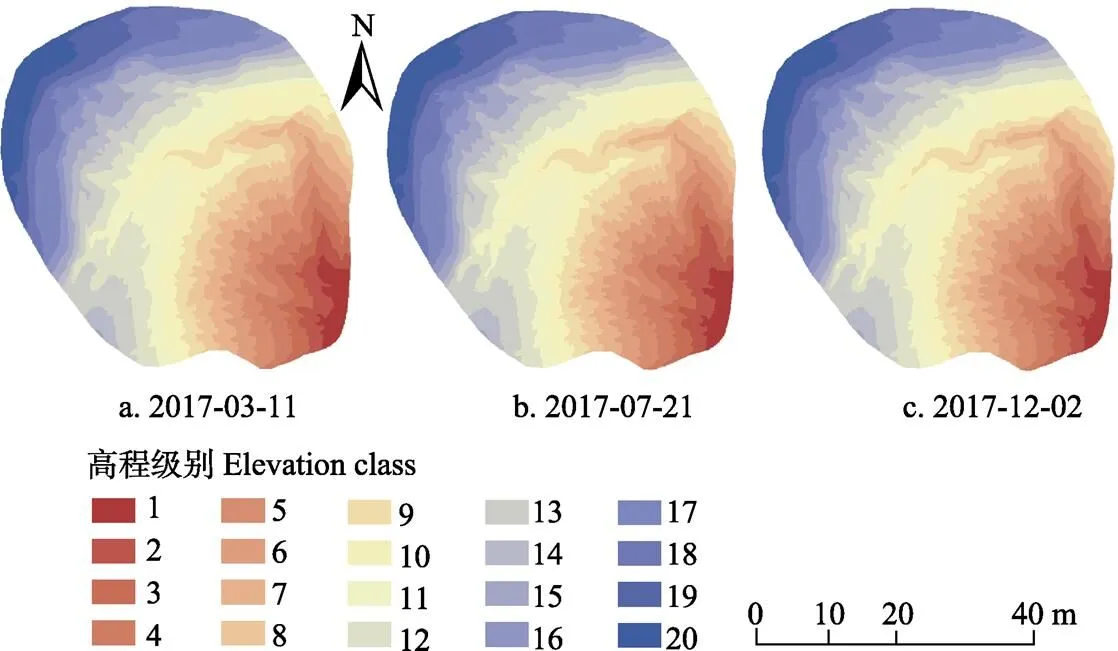
注：以2.25 m為間隔將案例崩崗劃分為20個高程級別，其中1為最低級別高程250~252.25 m，20為最高級別高程292.75~295 m。下同。

2）降雨量

降雨量作為修正轉移概率的指標在本研究中非常重要，與崩崗高程數據相應時間（2017年3月11日－2017年12月2日）的降雨量由放置在距離案例點約740 m的翻斗雨量計（Onset rg3-m）獲取，其精度為2 mm。

降雨情景需要根據研究區域的歷年降雨量記錄進行設置，從而使其分析結果具有代表性。而翻斗雨量計測定雨量的時間較短，不符合情景設置的要求。因此，采用福建省安溪縣第二次土壤普查成果《安溪土壤》[33]的降雨量記錄進行降雨情景的設置。

2.2 精度驗證

根據2017年3月11日和2017年7月21日的高程數據以及2017年3月11日－2017年7月21日和2017年7月21日－2017年12月2日的降雨量數據，對2017年12月2日的崩崗高程進行模擬并估算崩崗侵蝕量，然后與基于實測數據計算的崩崗侵蝕量進行對比，完成模擬精度和估算精度的驗證。

2.2.1 CA-Markov模型

1）面積檢驗

首先計算2017年3月11日和2017年7月21日的轉移概率矩陣，并根據該時段降雨量和2017年7月21日－2017年12月2日的降雨量進行轉換，將2017年3月11日和2017年7月21日的轉移概率矩陣轉換為2017年7月21日－2017年12月2日的轉移概率矩陣，如 表1所示。

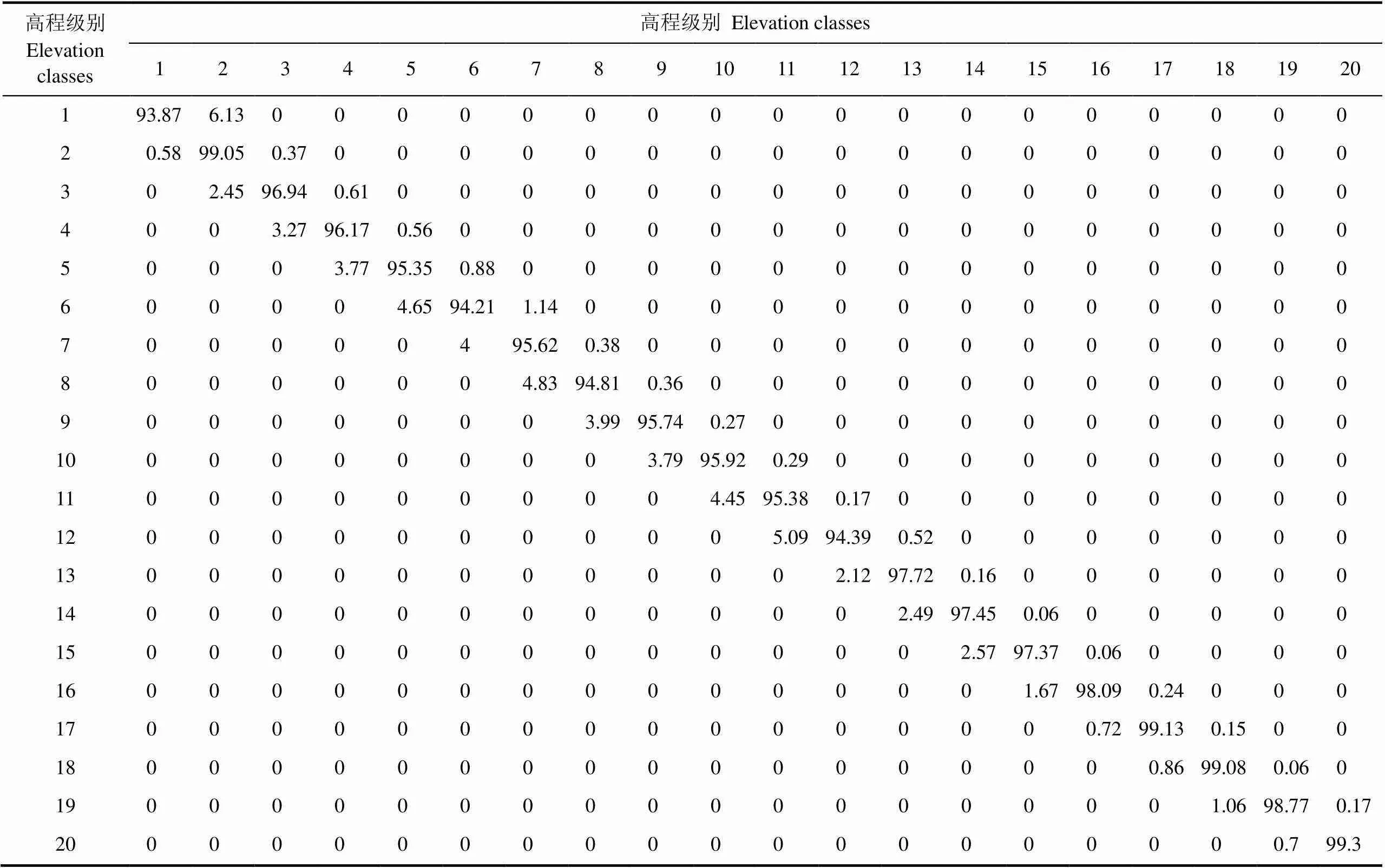
表1 2017年7月21日－2017年12月2日的轉移概率矩陣

然后根據轉移概率矩陣計算2017年12月2日時各高程級別面積的模擬值，并計算與實測高程的各級別面積（圖2）之間的誤差，面積誤差越小說明模擬精度越高，計算公式如下：

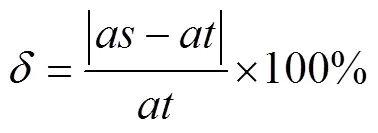
式中δ為面積誤差，%；as和at分別為高程級別面積的模擬值和實測值，m2。各高程級別的模擬值與實測值的面積誤差如圖3所示。

圖3中，各高程級別面積誤差平均為1.47%，除第1級高程的面積誤差較大（7.5%）外，其他級別的面積誤差均小于5%，說明高程級別的模擬面積精度較好，可以用于下一步的空間模擬。

2）空間檢驗

借助ArcGIS和Matlab軟件獲得CA-Markov模型所需參數，并完成2017年12月2日時案例崩崗高程級別的空間模擬，然后計算其Kappa系數。Kappa系數是通過模擬值與實測值之間的誤差矩陣計算得的，矩陣列表示實測類，矩陣行表示模擬類，矩陣中的數值表示像元數目，其計算公式如下：

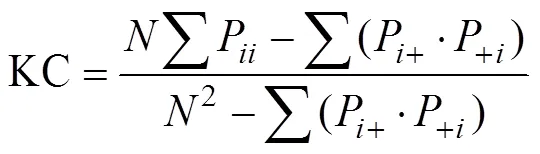
式中KC為Kappa系數；為樣本數目；P為第類被正確分類的樣本數目；P為第類所在列的像元數目；P為第類所在行的像元數目。當KC≥0.75時，兩圖的一致性較高，精度較高；當0.4≤KC<0.75時，精度一般；當KC<0.4時，精度較差。

根據公式（8）計算得總Kappa系數為0.958，說明該模型的模擬結果可靠。另外，各高程級別的Kappa系數如圖4。

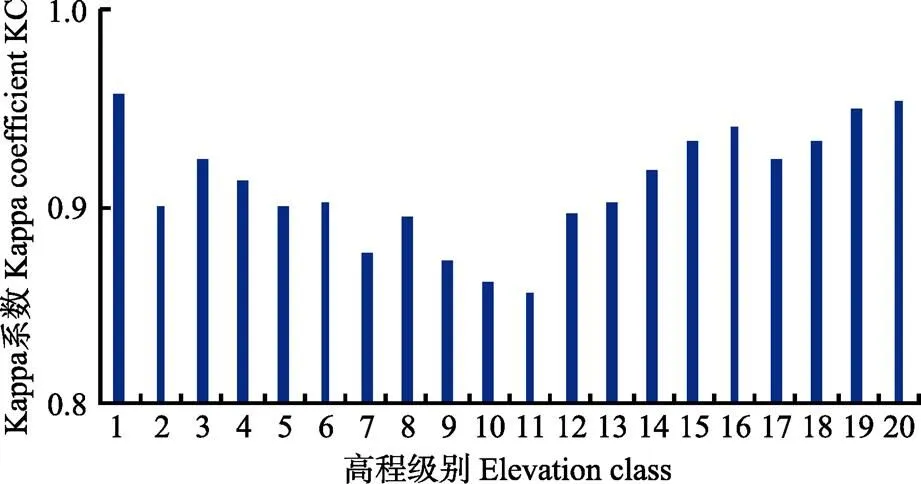
圖4 各高程級別的Kappa系數

由圖4可以看出各高程級別的Kappa系數均大于0.85，說明各高程級別的模擬精度均可接受。

2.2.2 ANUDEM內插

1）崩崗高程

對崗高程級別的CA-Markov模擬結果進行ANUDEM空間內插，將離散的高程級別轉化為連續的高程數據，即崩崗的模擬高程。然后與同期的實測高程進行對比，計算擬合度2和平均誤差ME用以檢驗精度，擬合度2用以驗證地形的整體還原度，平均誤差ME則用以反映地形細節的一致性，計算公式如下：

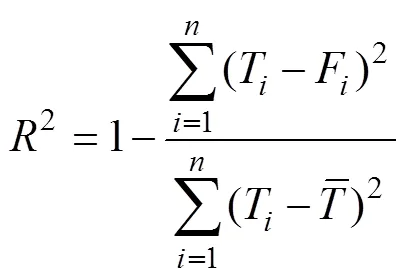
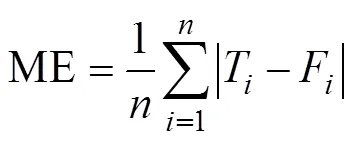
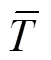
根據式（9）和式（10）計算出擬合度2為0.998 7，說明ANUDEM內插后的崩崗地形整體上還原較好，精度可以接受；但平均誤差ME為0.27 m，該值表示模擬高程與實測高程之間的平均差值，雖然數值較小，但相對于模擬期的崩崗地形變化較大。由此可以看出ANUDEM可以根據崩崗高程級別很好的還原崩崗的整體地貌形態，但對于崩崗地表細節刻畫的準確度一般。

2）崩崗侵蝕量

將模擬高程與基期高程疊加，根據式（6）計算出崩崗侵蝕量的模擬值；同時，將相同時段的無人機實測DEM疊加，根據式（6）計算出崩崗侵蝕量的實際值。由于ANUDEM對基于高程級別還原崩崗整體地貌的精度較高，但對其細節刻畫不夠理想。因此，為了使基期高程與模擬高程對崩崗地形的還原程度一致，對原始DEM進行級別劃分和ANUDEM內插處理。并將原始DEM和處理后的高程數據分別與模擬高程疊加，得崩崗侵蝕量的模擬值Ⅰ和模擬值Ⅱ。然后計算與實際值之間的誤差，記為誤差Ⅰ和誤差Ⅱ。計算結果如表2。

由表2可以看出，2個時段的誤差Ⅰ均較大，而2個時段的誤差Ⅱ均較小，僅為17.55%和8.66%，這一方面確認了模擬值Ⅱ的精度可以接受，另一方面進一步確認了ANUDEM對還原崩崗整體地形的可靠性，但對其細節的刻畫不夠。另外，可以看出2017年7月21日－2017年12月2日時段的2個誤差均大于2017年3月11日－2017年12月2日時段，這主要是由于后一時段的侵蝕量遠大于前一時段，而大量的侵蝕導致崩崗地形的變化較為顯著，減小了地形細節對計算侵蝕量的影響，從而提高的模擬精度。綜合而言，模擬值Ⅱ的精度較高，因此在估算崩崗侵蝕量時，選擇經過級別劃分和ANUDEM內插處理的高程為基期數據；并且，崩崗的實際侵蝕量越大，估算精度越高。

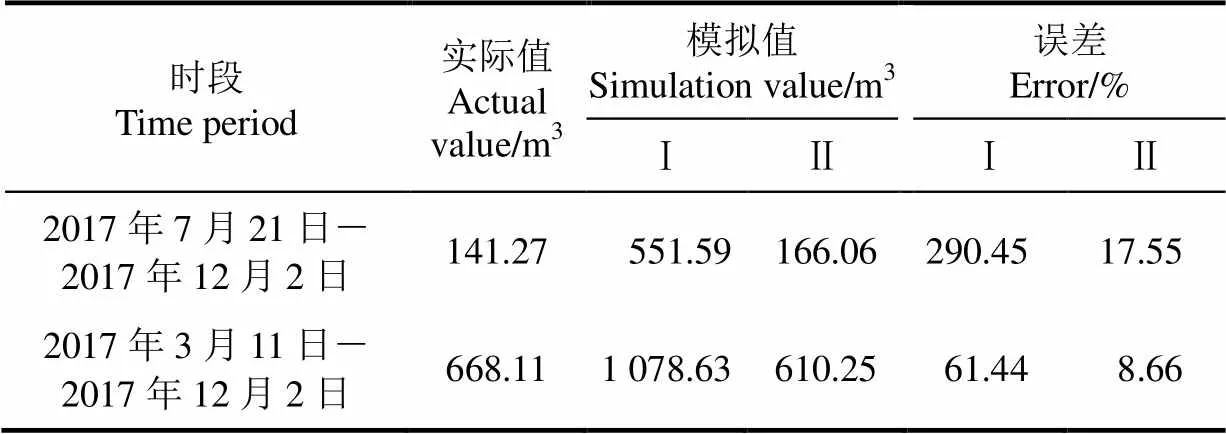
表2 崩崗侵蝕量的模擬精度

注：模擬值Ⅰ和誤差Ⅰ是以原始DEM為基期數據；模擬值Ⅱ和誤差Ⅱ是以級別劃分和內插處理后的高程為基期數據。

Note: Simulation Ⅰ and error Ⅰ are based on original DEM; Simulation Ⅱ and error Ⅱ are based on the elevation data processed by classification and interpolation.

2.3 崩崗侵蝕量預測

由于降雨是崩崗侵蝕的關鍵影響因素，因此本研究根據案例區歷年降雨數據設置了一般年景、干旱年景和多雨年景3個情景，分別對應年降雨量的平均值1 785 mm、最小值量1 546.2 mm和最大值2 023.8 mm。然后根據CA-Markov模型和ANUDEM空間內插，估算出這3個情景中案例崩崗的2017年12月2日－2018年12月2日的侵蝕量，即該崩崗的年侵蝕量。

2.3.1 崩崗高程級別預測

首先根據2017年3月11日－2017年12月2日計算出轉移概率矩陣，然后根據此時段的降雨量以及3個情景中2017年12月2日－2018年12月2日的降雨量對其進行轉換，得到3個情景中2017年12月2日－2018年12月2日的轉移概率矩陣。然后，應用CA-Markov模型對3個情景中2018年12月2日時崩崗高程級別進行空間模擬，如圖5。

2.3.2 崩崗侵蝕量預測

應用ANUDEM對2018年12月2日時崩崗高程級別預測圖進行內插，得到2018年12月2日時崩崗高程預測圖，如圖4。同時，對2017年12月2日時實測高程進行級別劃分與內插處理。然后，分別與3個情景中2018年12月2日時崩崗高程預測圖疊加，求得3個情景中，崩崗在2017年12月2日－2018年12月2日這一時段里的侵蝕量（年侵蝕量），如表3。

由表3可以看出，該崩崗在一般年景中的年侵蝕量為824.69 m3，即使在干旱年景時，該崩崗的年侵蝕量也有731.03 m3，說明該崩崗的泥沙產量巨大；該崩崗在2個極端情景之間的侵蝕量差值為193.54 m3，說明了不同降雨年景對崩崗泥沙產量的影響較大，在防治崩崗侵蝕修建攔沙壩時應考慮到不同降雨年景時侵蝕量的差異。

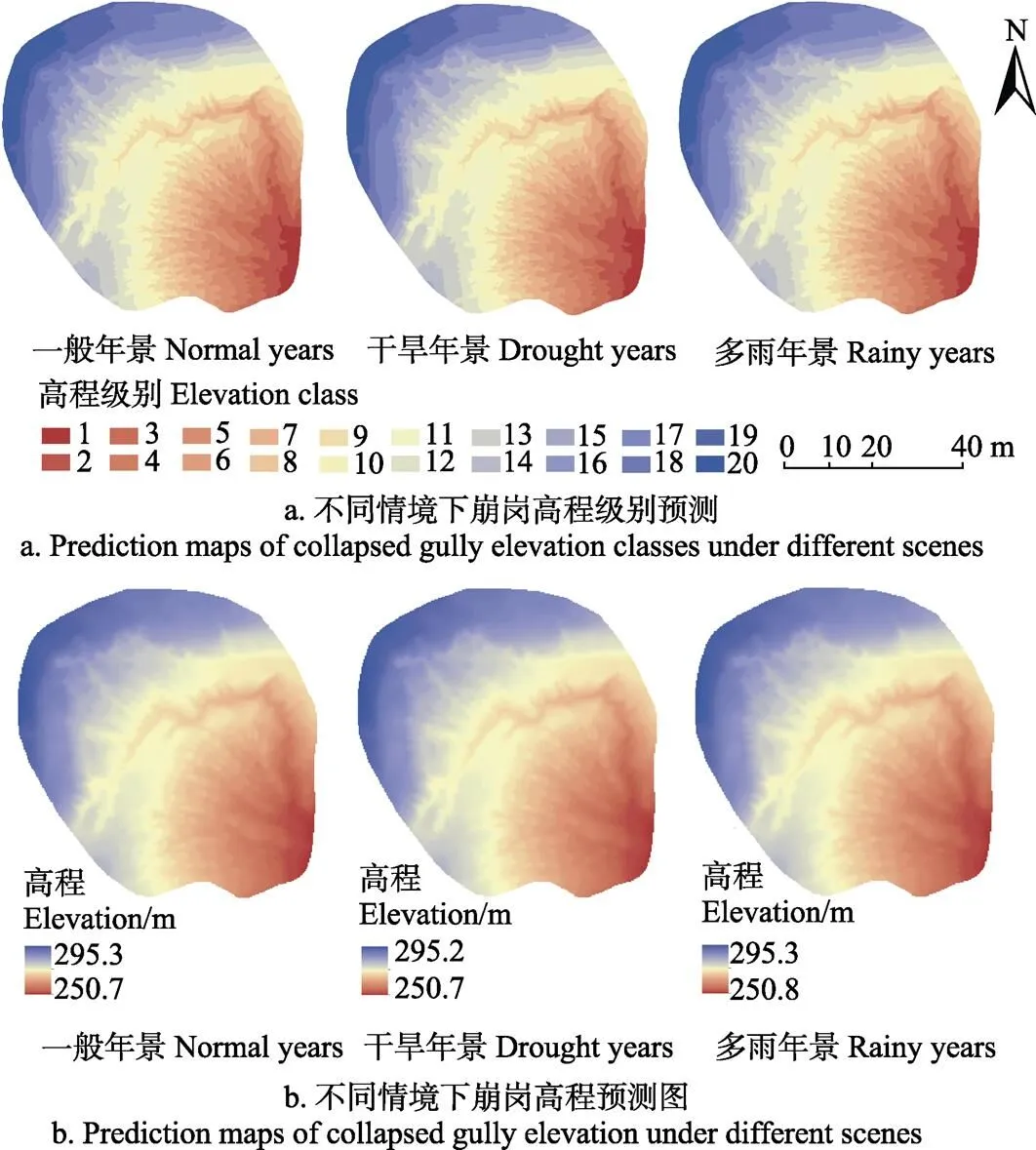
圖5 不同情景下崩崗高程級別預測圖和崩崗高程預測圖（2018-12-02）

表3 3個情景中崩崗2017年12月2日－ 2018年12月2日的侵蝕量

3 討 論

崩崗侵蝕劇烈，泥沙產量巨大，給當地的農業生產以及生態環境帶來威脅。但目前對崩崗侵蝕的研究側重于事后的治理工作，對崩崗侵蝕的預測、預警方面的研究相對較少。在實際的崩崗侵蝕治理工作中，多以修建堤壩攔截泥沙為主要途徑，而這更加大了對預測崩崗侵蝕量的需求。由于崩崗面積較小，且侵蝕劇烈地表變化迅速[10-11]，難以應用現有方法對其侵蝕量進行預估。因此，本研究在應用CA-Markov對崩崗高程級別的進行預測的基礎上，應用ANUDEM對高程級別進行空間內插實現對崩崗地形變化的預測，從而實現對崩崗侵蝕量的預估。不僅為預測和估算土壤侵蝕量提供新的思路和方法，并且為崩崗侵蝕的防治工作提供參考依據。

關于崩崗侵蝕量預測方面的研究相對較少，一般通過實測方式獲取崩崗侵蝕量，如劉希林等[32]借助三維激光掃描儀測得蓮塘崗崩崗（與案例崩崗相似）的3 a平均侵蝕量為833 m3，這與本所得結果非常接近。但由于不同崩崗的巖土及降雨等條件的影響，其侵蝕量也存在一定差異，且同一崩崗在不同時期其侵蝕量也不同。

CA-Markov為經驗型模型，根據上一時段變化預測下一時段變化，即將模擬的生態過程視為勻速過程。而崩崗侵蝕過程的驅動力主要來自于在時間尺度上較為多變的降雨，為此本研究選擇降雨量取代時間步長修正轉移概率矩陣，且模擬精度較高。同時由于該模型的經驗性，使經驗期和模擬期中降雨量對崩崗侵蝕的作用機制一致，因而難以探討不同降雨事件對崩崗侵蝕的作用。

有學者認為降雨強度對崩崗侵蝕也存在較為顯著[34-35]的作用，如Jiang等[34]通過室內試驗發現降雨強度與侵蝕泥沙顆粒的平均重量直徑成正比。但降雨量是降雨強度與降雨時長的綜合結果，與降雨強度相比，降雨量更適用于估算土壤侵蝕量[36]。但將降雨強度納入該模型中將會提高模擬精度，因而這方面還有待進一步研究。

另外，崩崗地表土壤的理化性狀以及如結皮等土壤方面的因素[37-38]，對崩崗侵蝕的空間差異性產生影響，但由于數據獲取困難，本研究在進行崩崗侵蝕量預估時未能考慮該因素。

4 結 論

1）根據崩崗侵蝕特征，構建了適用于模擬崩崗地形變化的CA-Markov模型。并通過對案例研究對其進行精度驗證：各高程級別面積誤差的平均值為1.47%，空間分布的總Kappa系數為0.958，各高程級別的Kappa系數均大于0.85，由此驗證了該模型對模擬崩崗高程級別變化的可靠性。

2）應用ANUDEM對崩崗高程級別進行內插，得到連續的崩崗模擬高程。通過與實測數據對比得到擬合度和平均誤差，分別為0.998 7和0.27 m，說明該方法雖然對崩崗地表細節的還原度一般，但對崩崗整體地形的還原度很高。

3）選擇了2種基期高程計算崩崗侵蝕量：原始DEM和經過級別劃分和內插處理的高程數據。通過與基于實測高程計算的侵蝕量對比發現，采用后者為基期數據計算得的崩崗侵蝕量更接近實際值，誤差為17.55%和8.66%；且實際侵蝕量越大，崩崗侵蝕量的估算精度更高。這主要是由于侵蝕越劇烈，地形改變越顯著，對還原地表細節的需要越低。

4）由于降雨量較難以預測，本研究根據案例點所在區域的歷史降雨數據設置了3種情景：一般年景、干旱年景和多雨年景。并對這3個情景中案例崩崗在2017年12月2日－2018年12月2日的侵蝕量（年侵蝕量）進行了預估，分別為824.69、731.03和924.57 m3。其中2個極端情景的侵蝕量之差較大，為193.54 m3，由此說明在修建崩崗攔沙壩時需考慮不同降雨年景時侵蝕量的差異。

[1] 水利部，中國科學院，中國工程院. 中國水土流失防治與生態安全[M]. 北京：科學出版社，2011：924－925.

[2] 梁音，寧堆虎，潘賢章，等. 南方紅壤區崩崗侵蝕的特點與治理[J]. 中國水土保持，2009 (1)：31－34. Liang Yin, Ning Duihu, Pan Xianzhang, et al. Characters and control of collapsing hill erosion in South China[J]. Soil and Water Conservation in China, 2009 (1): 31－34. (in Chinese with English abstract)

[3] 牛德奎. 華南紅壤丘陵區崩崗發育的環境背景與侵蝕機理研究[D]. 南京：南京林業大學，2009. Niu Dekui. Research on the Environmental Factors and Erosive Mechanism of Collapsing Hill in South China[D]. Nanjing : Nanjing Forestry University, 2009. (in Chinese with English abstract)

[4] 王禮先，孫保平，余新曉，等. 中國水利百科全書——水土保持分冊[M]. 北京：中國水利水電出版社，2004：48－49.

[5] 王學強，蔡強國. 崩崗及其治理措施的系統分析[J]. 中國水土保持，2007(7)：29－31. Wang Xueqiang, Cai Qiangguo. Systematic analysis on dilapidated granite and measures for management[J]. Soil and Water Conservation in China, 2007(7): 29－31. (in Chinese with English abstract)

[6] 趙明松，李德成，張甘霖，等. 基于RUSLE模型的安徽省土壤侵蝕及其養分流失評估[J]. 土壤學報，2016，53(1)：28－38. Zhao Mingsong, Li Decheng, Zhang Ganlin, et al. Evaluation of soil erosion and soil nutrient loss in Anhui Province based on RUSLE Model[J]. Acta Pedologica Sinica, 2016, 53(1): 28－38. (in Chinese with English abstract)

[7] Kazuya Yoshimura, Yuichi Onda, Hiroaki Kato. Evaluation of radiocaesium wash-off by soil erosion from various land uses using USLE plots[J]. Journal of Environmental Radioactivity, 2015, 139: 362－369.

[8] 賈寧鳳，段建南，李保國，等. 基于 AnnAGNPS模型的黃土高原小流域土壤侵蝕定量評價[J]. 農業工程學報，2006，22(12)：23－27. Jia Ningfeng, Duan Jiannan, Li Baoguo, et al. Soil erosion quantitative evaluation of small watershed in Loess Plateau based on AnnAGNPS model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(12): 23－27. (in Chinese with English abstract)

[9] 于國強，李占斌，李鵬，等. 黃土高原小流域重力侵蝕數值模擬[J]. 農業工程學報，2009，25(12)：74－79. Yu Guoqiang, Li Zhanbin, Li Peng, et al. Numerical simulation on gravitational erosion of small watershed system in Loess Plateau[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(12): 74－79. (in Chinese with English abstract)

[10] 阮伏水. 福建省崩崗侵蝕與治理模式探討[J]. 山地學報，2003，21(6)：675－680. Ruan Fushui. Study on slump gully erosion and its control in Fujian Province[J]. Journal of Mountain Science, 2003, 21(6): 675－680. (in Chinese with English abstract)

[11] 林敬蘭，陳志明，黃炎和，等. 安溪縣崩崗侵蝕空間分布特征探討[J]. 水土保持研究，2009，24(6)：63－68. Lin Jinglan, Chen Zhiming, Huang Yanhe, et al. Study on the charactistics of spatial distribution of slope disintegration erosion in Anxi County[J]. Research of Soil and Water Conservation, 2009, 24(6): 63－68. (in Chinese with English abstract)

[12] Marco Cavalli, Barbara Goldin, Francesco Comiti, et al. Assessment of erosion and deposition in steep mountain basins by differencing sequential digital terrain models[J]. Geomorphology, 2017, 291：4－16.

[13] 劉希林，張大林. 基于三維激光掃描的崩崗侵蝕的時空分析[J]. 農業工程學報，2015，31(4): 204－211. Liu Xilin, Zhang Dalin. Temporal－spatial analyses of collapsed gully erosion based on three－dimensional laser scanning[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(4)：204－211. (in Chinese with English abstract)

[14] Aliakbar Nazari Samani, Hassan Ahmadi, Mohammad Jafari, et al. Geomorphic threshold conditions for gully erosion in Southwestern Iran (Boushehr－Samal watershed)[J]. Journal of Asian Earth Sciences, 2009, 35(2): 180－189.

[15] Kakembo Vincent, Xanga WW, Rowntree Katharine. Topographic thresholds in gully development on the hill slopes of communal areas in Ngqushwa Local Municipality, Eastern Cape, South Africa[J]. Geomorphology, 2009, 110 (3/4): 188－194.

[16] Antonina Capra, Paolo Porto, Baldassare Scicolone, et al. Relationships between rainfall characteristics and ephemeral gully erosion in a cultivated catchment in Sicily (Italy)[J]. Soil and Tillage Research, 2009, 105(1): 77－87.

[17] 蔣芳市. 花崗巖崩崗崩積體侵蝕機理研究[D]. 福州：福建農林大學，2013. Jiang Fangshi. Erosion Mechanism of Colluvial Deposits in Granite Benggang[D]. Fuzhou: Fujian Agriculture and Forestry University, 2013. (in Chinese with English abstract)

[18] Kuswantoro Marko, Faris Zulkarnain, Eko Kusratmoko. Coupling of Markov chains and cellular automata spatial models to predict land cover changes (case study: upper Ci Leungsi catchment area)[C]// IOP Conference Series: Earth and Environmental Science. Bristol, England: IOP Publishing Ltd, 2017: 012032.

[19] Zhou De, Lin Zhulu, Liu Liming. Regional land salinization assessment and simulation through cellular automaton－markov modeling and spatial pattern analysis[J]. Science of the Total Environment, 2012, 439: 260－274.

[20] 季翔，劉黎明，李洪慶. 基于生命周期的鄉村景觀格局演變的預測方法——以湖南省金井鎮為例[J]. 應用生態學報，2014，25(11)：3270－3278. Ji Xiang, Liu Liming, Li Hongqing. Prediction method of rural landscape pattern evolution based on life cycle: A case study of Jinjing Town, Hunan Province, China[J]. Chinese Journal of Applied Ecology, 2014, 25(11): 3270－3278. (in Chinese with English abstract)

[21] Liu Ruimin, Men Cong, Wang Xiujuan, et al. Application of spatial Markov chains to the analysis of the temporal-spatial evolution of soil erosion[J]. Water Sci Technol, 2016, 74(5): 1051－1059.

[22] Rhonda Skaggs, Soumen Ghosh. Assessing changes in soil erosion rates: A Markov chain analysis[J]. Journal of Agricultural and Applied Economics, 2009, 31(3): 611－622.

[23] 王俊，江帆，朱長青，等. 利用等高線柵格化的DEM精度評估[J]. 武漢大學學報·信息科學版，2009，34(8)： 952－955. Wang Jun, Jiang Fan, Zhu Changqing, et al. Estimate the accuracy of DEM based on reconstructed contours[J]. Geomatics and Information Science of Wuhan University, 2009, 34(8): 952－955. (in Chinese with English abstract)

[24] 張笑，陳剛，段淼然，等. 南方復合地貌區DEM內插算法的對比研究[J]. 水土保持研究，2015，22(5)：106－112. Zhang Xiao, Chen Gang, Duan Miaoran, et al. Comparative study of different DEM interpolation algorithms in the southern complex geomorphologic zone[J]. Research of Soil and Water Conservation, 2015, 22(5): 106－112. (in Chinese with English abstract)

[25] 徐亞莉，羅明良，梁倍瑜，等. DEM 空間插值方法對土壤侵蝕模擬的影響研究：以USPED分析干熱河谷典型沖溝為例[J]. 地理科學進展，2016，35(7)：870－877. Xu Yali, Luo Mingliang, Liang Beiyu, et al. Effects of different DEM spatial interpolation methods on soil erosion simulation: A case study of a typical gully of dry－hot valley based on USPED[J]. Progress in Geography, 2016, 35(7): 870－877. (in Chinese with English abstract)

[26] 劉希林，張大林. 崩崗土體剖面水分分布特征及變化規 律：以廣東五華縣蓮塘崗崩崗為例[J]. 熱帶地理，2015，35(3)：291－297. Liu Xilin, Zhang Dalin. Distribution characteristics and spatial variation of Benggang soil moistures: A case study of Liantanggang in Wuhua County, Guangdong[J]. Tropical Geography, 2015, 35(3): 291－297. (in Chinese with English abstract)

[27] 史德明. 我國熱帶、亞熱帶地區崩崗侵蝕的剖析[J]. 水土保持學報，1992，6(4)：32－37. Shi Deming. Analysis of collapsing erosion in tropical and subtropical regions of China[J]. Journal of Soil and Water Conservation, 1992, 6(4): 32－37. (in Chinese with English abstract)

[28] 林敬蘭，黃炎和，張德斌，等. 水分對崩崗土體抗剪切特性的影響[J]. 水土保持學報，2013，27(3)：55－58. Lin Jinglan, Huang Yanhe, Zhang Debin, et al. Influence of soil moisture content on shear characteristics of Benggang[J]. Journal of Soil and Water Conservation, 2013, 27(3): 55－58. (in Chinese with English abstract)

[29] Vincent Chaplot, James Brown, Phumlani Dlamini, et al. Rainfall simulation to identify the storm-scale mechanisms of gully bank retreat[J]. Agricultural Water Management, 2011, 98: 1704－1710.

[30] 蔣芳市，黃炎和，林金石，等. 坡度和雨強對崩崗崩積體侵蝕泥沙顆粒特征的影響[J]. 土壤學報，2014，51(5)： 974－982. Jiang Fangshi, Huang Yanhe, Lin Jinshi, et al. Effects of slope gradient and rainfall intensity on particle size composition of erosion sediment form conlluvial deposits of Benggang[J]. Acta Pedologica Sinca. 2014, 51(5): 974－982. (in Chinese with English abstract)

[31] 劉希林，張大林，賈瑤瑤. 崩崗地貌發育的土體物理性質及其土壤侵蝕意義：以廣東五華縣蓮塘崗崩崗為例[J]. 地球科學進展，2013，28(7)：802－811. Liu Xilin, Zhang Dalin, Jia Yaoyao. Soil physical properties of collapsing hill and gully and their indications for soil erosion: An example of Liantanggang collapsing hill and gully in Wuhua county of Guangdong[J]. Advances in Earth Science, 2013, 28(7): 802－811. (in Chinese with English abstract)

[32] 劉希林，張大林. 崩崗地貌侵蝕過程三維立體監測研 究：以廣東五華縣蓮塘崗崩崗為例[J]. 水土保持學報，2015，29(1)：26－31. Liu Xilin, Zhang Dalin. Study on erosion process of collapsing hill and gully by Three-dimensional Monitoring: An example of Liantanggang in Wuhua County of Guangdong Province[J]. Journal of Soil and Water Conservation, 2015, 29(1): 26－31. (in Chinese with English abstract)

[33] 福建省安溪縣土壤普查辦公室. 安溪土壤[R]. 1984.

[34] Jiang Fangshi, Huang Yanhe, Wang Mingkuang, et al. Effects of rainfall intensity and slope gradient on steep colluvial deposit erosion in Southeast China[J]. Soil Science Society of America Journal, 2014, 78(5): 1741－1752.

[35] 熊傳祥，王濤，魯曉兵. 降雨作用下崩崗形成細觀機理模擬[J]. 山地學報，2013，31(6)：710－715. Xiong Chuanxiang, Wang Tao, Lu Xiaobing. Meso-mechanical simulation of slope disintegration erosion under rainfall[J]. Journal of Mountain Science, 2013, 31(6): 710－715. (in Chinese with English abstract)

[36] 彭雙云，楊昆，洪亮，等. 基于 USLE 模型的滇池流域土壤侵蝕時空演變分析[J]. 農業工程學報，2018，34(10)：138－146. Peng Shuangyun, Yang Kun, Hong Liang, et al. Spatio- temporal evolution analysis of soil erosion based on USLE model in Dianchi Basin[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(10): 138－146. (in Chinese with English abstract)

[37] 程琴娟，蔡強國，李家永. 表土結皮發育過程及其侵蝕響應研究進展[J]. 地理科學進展，2005，24(4)：114－122. Cheng Qinjuan, Cai Qiangguo, Li Jiayong. Summarization on study of soil surface crust or sealing and its effects on erosion[J]. Process in Geography, 2005, 24(4): 114－122. (in Chinese with English abstract)

[38] 蔣芳市，黃炎和，林金石，等. 花崗巖崩崗崩積體顆粒組成及分形特征[J]. 水土保持研究，2014，21(6)：175－180. Jiang Fangshi, Huang Yanhe, Lin Jinshi, et al. Soil particle size distribution and fractal dimensions of colluvial deposits in granite Benggang[J]. Research of Soil and Water Conservation, 2014, 21(6):175－180. (in Chinese with English abstract)

Estimation of erosion amount in collapsed gully based on CA-Markov model and ANUDEM interpolation

Ji Xiang1,2, Huang Yanhe1※, Lin Jinshi1, Jiang Fangshi1, Yu Mingming1, Li Shaoxin1

(1.350002,; 2.350002,)

Collapsed gully is a kind of soil erosion in South China threating agriculture production and ecological environment due to its considerable sediment yield. Therefore, the prediction and estimation of erosion amount play a significant role in its prevention and control. However, collapsed gullies normally cover a relatively smaller area and eroded more severely than other kinds of soil erosion, which made existing methods and approaches hardly to apply on it. In this research, cellular automation-Markov (CA-Markov) model and Australian National University digital elevation model (ANUDEM) are employed to estimate and predict the erosion amount of collapsed gully. The former is taken to simulate the transition of collapsed gully elevation classes, and the latter is taken to spatial interpolate on the simulation results of collapsed gully elevation classes. Based on the two processes, the continuous elevation data of collapsed gully can be simulated and predicted. Then the erosion amount is computed according to the prediction result and base time data. To test this approach, a collapsed gully located in the Longmen Town, Anxi County, Fujian Province is chosen as the case study. And it contains two parts, which are the confirmation of simulating accuracy and the prediction under 3 types of scenes for annual erosion amount. The results show that the modified CA-Markov model performances well on the simulation of collapsed gully elevation classes, which resulted from a lower area error between simulation results and actual value (1.47%), and a higher Kappa coefficient of 0.958. The goodness of fit (2) of the interpolation result using ANUDEM is 0.998 7 and its mean error (ME) is 0.27 m, which means ANUDEM is good at the integral restoration of collapsed gullies terrain but not sufficient at details. As a consequence, two types elevation at the base time are chosen to estimate the erosion amount, one is original DEM, and the other one is the elevation data through classes division and interpolated processing. The erosion amount calculated from the second type of base data performances difference rates of 17.55% and 8.66%, which are much lower than the one derived from the first type of base data. Thus, the second type of base data is accessible for computing collapsed gully erosion amount, and the huger the real erosion amount, the higher the accuracy. After the confirmation of modeling accuracy, 3 types of rainfall scenes were set based on the historical records of rainfall, which are normal years, drought years and rainy years. The annual erosion amounts of case collapsed gully under the 3 types of rainfall scenes are 824.69, 731.03 and 924.57 m3, and the difference of the two extreme rainfall scenes is 193.54 m3, which means that the difference of erosion amount between different rainfall scenes should be taken into account when building a sediment storage dam to control the damage of a collapsed gully. The methods proposed in this research can not only provide a novel way to study the erosion process and erosion amount of collapsed gully, but also supply a reasonable reference for the prevention and control of collapsed gully erosion.

erosions; models; collapsed gully; erosion amount; CA-Markov; ANUDEM

10.11975/j.issn.1002-6819.2018.21.016

S157

A

1002-6819(2018)-21-0128-09

2018-05-18

2018-09-17

國家自然科學基金項目（41601557; 41571272）；國家科技支撐計劃項目（2014BAD15B0303）

季 翔，講師，博士，主要從事景觀生態及水土保持研究。 Email：jixiangss@126.com

黃炎和，教授，博士，主要從事水土保持和崩崗侵蝕研究。 Email：yanhehuang@163.com

季 翔，黃炎和，林金石，蔣芳市，余明明，李紹鑫. 基于CA-Markov模型與ANUDEM內插法的崩崗侵蝕量預估[J]. 農業工程學報，2018，34(21)：128－136. doi：10.11975/j.issn.1002-6819.2018.21.016 http://www.tcsae.org

Ji Xiang, Huang Yanhe, Lin Jinshi, Jiang Fangshi, Yu Mingming, Li Shaoxin. Estimation of erosion amount in collapsed gully based on CA-Markov model and ANUDEM interpolation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(21): 128－136. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.21.016 http://www.tcsae.org