需求可拆分的節(jié)點具有雙重需求的車輛路徑問題研究進(jìn)展

，

(中南大學(xué) 交通運輸工程學(xué)院， 湖南 長沙 410075)

一般車輛路徑問題(vehicle routing problem，VRP)中各客戶點僅具有送貨需求或取貨需求， 即純送(取)貨車輛路徑問題。 隨著逆向物流的快速發(fā)展及環(huán)保政策的切實落實， 實際操作中需要對一部分客戶點送貨， 對另一部分客戶點取貨， 于是產(chǎn)生了取送貨問題(general pickup and delivery problem，GPDP)。 無論是VRP還是GPDP， 客戶更愿意接受以盡可能少的服務(wù)訪問次數(shù)下完成所有需求。 目前大部分的研究都是針對每個客戶點的需求只能由一輛車服務(wù)， 即需求不可拆分的問題類型， 但是， 在實際運行中，客戶需求被拆分運輸?shù)那闆r并不少見，例如不同貨物需要不同的運輸工具及裝卸設(shè)備，將客戶需求根據(jù)貨物類型特性分類運輸， 可提高作業(yè)物流作業(yè)效率。 具有集中管理制度的中心物流配送中心可以為需求拆分運輸模式提供技術(shù)及設(shè)備支持。

已有理論研究及事實證明，需求可拆分的運輸方式有利于充分利用車輛裝載能力和降低車輛行駛成本。Dror等[1-3]首次提出需求可拆分的純送(取)貨車輛路徑問題(split delivery vehicle routing problem，SDVRP)，此后越來越多學(xué)者致力于需求可拆分問題領(lǐng)域的研究，但是較少有針對GPDP需求可拆分問題類型的研究。2005年，Mitra[4]和Nowak[5]分別就不同類型GPDP考慮需求可拆分的運輸模式，開啟了需求可拆分的取送貨問題(GPDP with split loads，GPDPSL)的研究。本文中提出了適用于各種節(jié)點具有雙重需求的車輛路徑問題(SVRPNDD)的數(shù)學(xué)模型，分析比較各種問題的特性，并歸納總結(jié)各種問題算法的研究進(jìn)展。

1 GPDP分類

在已有研究中，不同學(xué)者從不同角度、不同準(zhǔn)則對GPDP進(jìn)行分類。大部分GPDP中假設(shè)所有客戶點均只能被訪問一次，即需求不可拆分類型。借鑒Parragh等[6-7]提出的分類準(zhǔn)則，本文中將GPDP劃分為2個不同問題類型。在第1類問題中，所有配送貨品必須由單一(或多個)配送中心發(fā)送至各收貨客戶點，且從各具有發(fā)貨需求的客戶點收集的貨品必須全部運送回配送中心，此類問題統(tǒng)稱為帶回程的車輛路徑問題(vehicle routing problems with backhauls，VRPB)。需要說明的是，目前大部分VRPB的經(jīng)典定義是假設(shè)運輸方式為“先取后送”形式，在Parragh等[6-7]的問題定義及分類中，歸類為帶聚類回程的車輛路徑問題(VRP with all linehauls before backhauls或VRP with clustered backhauls，VRPCB)。在第2類問題中，取送貨需求存在于各客戶點之間，本文中定義為收發(fā)問題(pickup and delivery problem，PDP)。借鑒王科峰等[8-10]的研究，本文中根據(jù)客戶節(jié)點具有的需求類型情況，進(jìn)一步將VRPB細(xì)分為節(jié)點具有單一需求的車輛路徑問題(VRP with nodes of single demand，VRPNSD)及節(jié)點具有雙重需求的車輛路徑問題(VRP with nodes of double demands，VRPNDD)。VRPNSD中所有客戶點只能具有取貨或送貨中的一種需求，而VRPNDD中客戶點可同時具有取貨及送貨2種需求。PDP根據(jù)發(fā)、收貨客戶是否對應(yīng)分為2個子類，即不對稱的PDP及對稱的PDP。為了便于理解，將GPDP分類進(jìn)行歸納，如圖1所示。

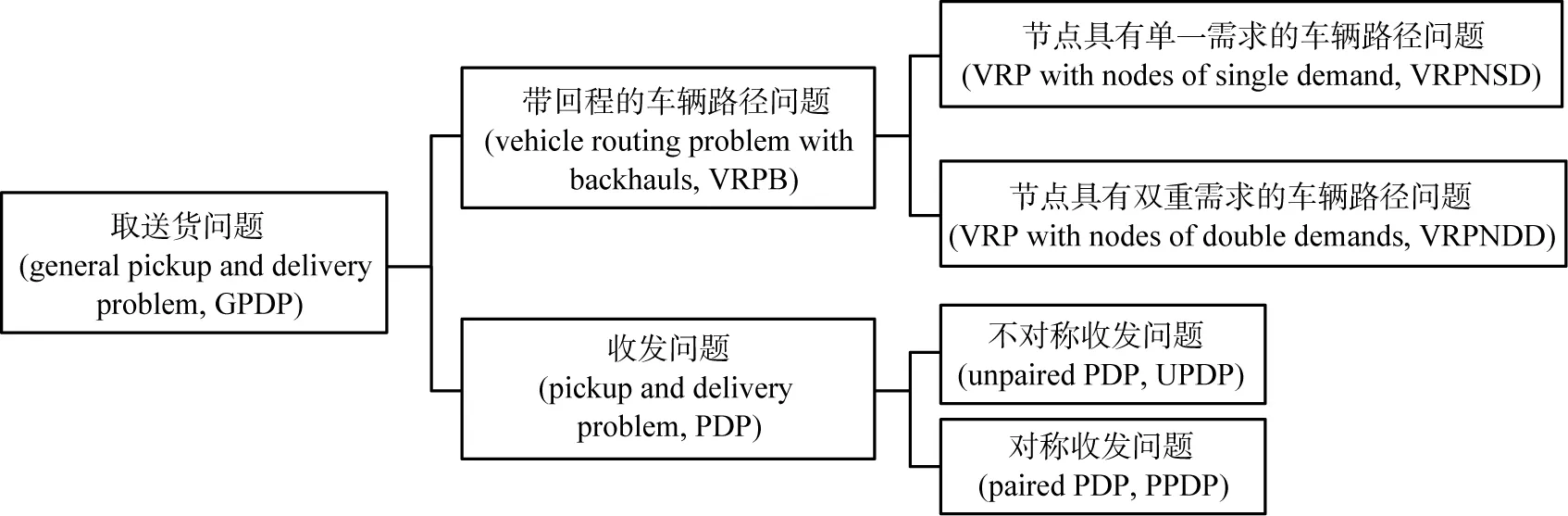
圖1 取送貨問題分類

1.1 VRPNSD概述

VRPNSD中的客戶被分為配送客戶(只具有送貨需求)及集取客戶(只具有取貨需求)。假設(shè)所有客戶集為N，配送客戶集為D，集取客戶集合為P，則有N=D∪P且D∩P=○/。若任意車輛只有在訪問完路徑中的所有配送客戶后才能開始對集取客戶進(jìn)行訪問，則稱此類問題為VRPCB。如果問題對送貨服務(wù)及取貨服務(wù)順序無約束，則為混合取送貨車輛路徑問題(VRP with mixed linehauls and backhauls，VRPMB)。

1.2 VRPNDD概述

VRPNDD中客戶可同時具有取貨及送貨2種需求，即客戶可能既是配送客戶，也是集取客戶。同時取送貨的車輛路徑問題(VRP with simultaneous delivery and pickup，VRPSDP)是VRPNDD的代表類型。值得注意的是，VRPSDP假設(shè)所有客戶需求均不得大于車輛最大裝載能力。

Parragh等[6-7]將取送貨可分割的車輛路徑問題(VRP with divisible delivery and pickup，VRPDDP)列入VRPB中，VRPDDP中同時具有取貨及送貨需求的客戶，允許被訪問2次，一次完成取貨服務(wù)，一次完成送貨服務(wù)，即客戶需求可能被拆分成2次。由于本文中假設(shè)GPDP中所有客戶不允許被拆分運輸，因此將VRPDDP列為VRPNDD類型。

2 GPDPSL的研究現(xiàn)狀

針對GPDPSL的研究，Mosheiov[11]于1998年最早提出了單位需求(single-unit demand)的假設(shè)。在此假設(shè)下，客戶的任意需求(取或送)均可以最小計量單位進(jìn)行拆分，從而由多輛車運輸。Nagy等[12]雖然在研究中未直接考慮GPDPSL，但是針對GPDP特別設(shè)計了一組算法求解鄰域，其中包括“Neck”與“Unneck”一組對偶算子，分別用于對客戶需求進(jìn)行拆分及合并。

GPDPSL研究的正式開端可追溯至2005年，Mitra[4]首次將需求可拆分運輸方式引入VRPSDP中， 并在文獻(xiàn)[13]中正式定義該類問題為需求可拆分的同時取送貨車輛路徑問題(vehicle routing problem with split pickups and deliveries，VRPSPDP)。更多學(xué)者也致力于GPDPSL領(lǐng)域研究，包括研究其求解難度、問題特性、最優(yōu)解特性及求解算法等。圖2所示為全球在GPDPSL領(lǐng)域研究論文的發(fā)表數(shù)量。從圖中可以看出，該問題在早期的研究成果相對較少，近年來呈增長趨勢。

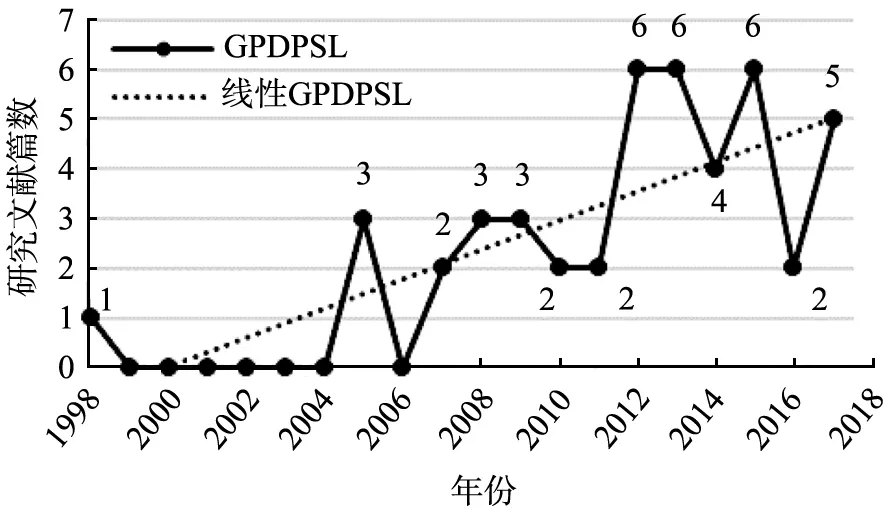
圖2 需求可拆分的取送貨問題(GPDPSL)研究論文發(fā)表情況

已知GPDP分為2個大類，本文中也相應(yīng)地將GPDPSL分為2類，即需求可拆分的帶回程的車輛路徑問題(VRPB with split loads，VRPBSL)及需求可拆分的收發(fā)車輛路徑問題(PDP with split loads，PDPSL)。已有研究中，PDPSL的研究熱度略高于VRPBSL的，兩者的比例大致為56∶44。

2.1 VRPBSL研究現(xiàn)狀

VRPBSL同樣可以分為2大類，即需求可拆分的VRPNSD(split VRPNSD，SVRPNSD)及需求可拆分的VRPNDD(split VRPNDD，SVRPNDD)。自Mitra[4]開始VRPSPDP研究以來，隨后更多學(xué)者聚焦VRPBSL領(lǐng)域研究。Lai等[14]將需求可拆分操作模型引入VRPCB，提出需求可拆分的VRPCB(split VRPCB，SVRPCB)，這也是目前針對SVRPNSD的唯一研究文獻(xiàn)。可見，絕大多數(shù)的VRPBSL研究均是針對SVRPNDD的，其比例約占95%。本文中分析認(rèn)為，這是因為SVRPNDD更加貼合實際運輸活動的復(fù)合型，所以具有更重要的研究意義及更強的實用性。如果假設(shè)SVRPNDD中具有雙重需求的客戶中的某一項需求為0，則SVRPNDD即可轉(zhuǎn)換成SVRPNSD。

2.2 PDPSL研究現(xiàn)狀

2005年Nowak[5]首次針對PDPSL進(jìn)行研究，并在后續(xù)幾年繼續(xù)對該領(lǐng)域進(jìn)行較全面的研究[15-17]。在已有研究中，針對PDPSL的研究大部分是基于實際應(yīng)用問題的，特別是應(yīng)用于海上商貿(mào)運輸，其比例約占60%，其余的32%、8%分別是關(guān)于理論及算法和其他應(yīng)用。近年來，PDPSL研究問題呈現(xiàn)較大的個性化趨勢，這里不進(jìn)行詳盡闡述。

3 SVRPNDD研究進(jìn)展

目前大部分SVRPNDD研究以VRPSPDP問題為主，其比例占到85%，其中Mitra[4,13]為VRPSPDP的研究奠定了基礎(chǔ)，王科峰等[8-10]深入研究VRPSPDP問題特性，為該問題研究提供了更加詳盡的理論依據(jù)。文獻(xiàn)[18-19]中在解決現(xiàn)實第三方物流案例時采用VRPSPDP模型，考慮時間窗限制，提出了帶時間窗的VRPSPDP(VRPSPDP with time windows，VRPSPDPTW)。Yin等[20]提出一種特殊的VRPSPDP，對各客戶點拆分次數(shù)進(jìn)行限制(最多只能被拆分2次)，且行駛路徑不能超過最大長度的限制。2017年，Wassan等[21]將VRPDDP以需求可拆分類型問題呈現(xiàn)在學(xué)者面前，Nagy等[22]進(jìn)而就VRPDDP需求可拆分特性進(jìn)行深入、全面的研究，拓展了研究領(lǐng)域。2005—2017年12月全球SVRPNDD領(lǐng)域研究論文的發(fā)表情況如圖3所示。

3.1 問題描述與數(shù)學(xué)模型

SVRPNDD可統(tǒng)一表示為無向圖G=(V，E)，其中V={0，1，2，…，n}代表配送中心及客戶點的集合，其中0表示配送中心，{1,2,…,n}表示客戶點的集合；E表示邊集。

SVRPNDD旨在滿足下列約束條件的情況下求得最小運輸成本(使用最少車輛數(shù)使得行駛總路程最短)：

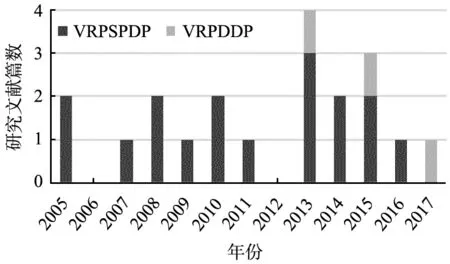
VRPSPDP—需求可拆分的同時取送貨車輛路徑問題；VRPDDP—取送貨可分割的車輛路徑問題。

1) 所有車輛離開同一車場， 并最終返回該車場；

2)所有車輛裝載能力相同，車輛的實際裝載量不得超過該車最大裝載能力；

3)各客戶點可同時具有收取、發(fā)送2種需求，且任意類型需求量可能大于車輛裝載能力；

4)客戶總需求量可同時被不只一輛車訪問，或被同一輛車服務(wù)1次以上；

5)任意車輛對客戶點取、送服務(wù)無順序要求；

6)無時間窗及最長路徑距離限制。

通常認(rèn)為，多用一輛車所產(chǎn)生的固定費用總是超過總行駛費用減少帶來的節(jié)省，因此即使存在不進(jìn)行最小車輛數(shù)限制，可能求解得到總行駛距離更短的情況，問題仍然設(shè)定最小車輛數(shù)K為已知參數(shù)。最小車輛數(shù)為

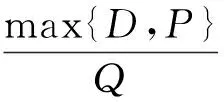
式中：「?表示向上取整；D為總送貨量；P為總?cè)∝浟浚籕為車輛最大裝載能力。

大部分考慮帶時間窗的問題初始條件并未設(shè)定最小車輛數(shù)約束，原因是增加時間窗約束會導(dǎo)致問題求解變得更加困難。為了能在接受的時間內(nèi)得到滿意解，允許使用盡可能少而非最少的車輛完成服務(wù)，但是，Tang等[18]得出結(jié)論是，在一個時間窗內(nèi)，需要的最小車輛數(shù)與非時間窗約束下問題使用的最小車輛數(shù)相等，且在一個時間窗內(nèi)，存在一個可行方案，其所需車輛數(shù)為問題最小車輛數(shù)。

SVRPNDD數(shù)學(xué)模型符號說明見表1。

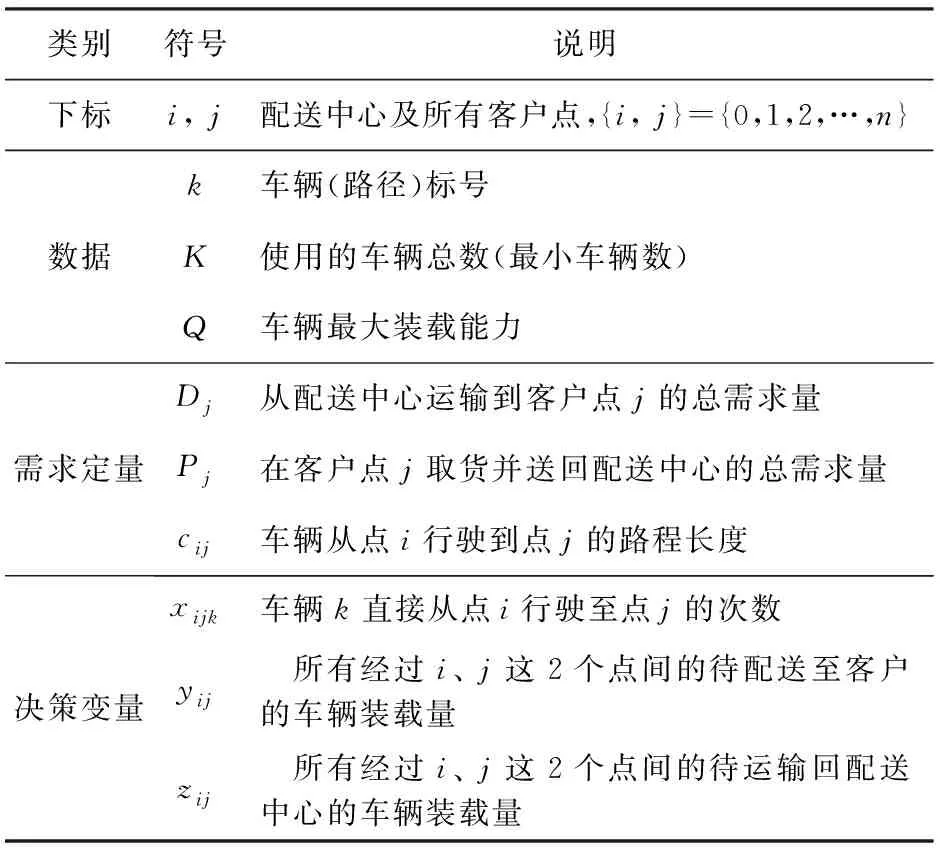
表1 需求可拆分的同時取送貨車輛路徑問題的數(shù)學(xué)模型符號及說明

SVRPNDD的數(shù)學(xué)模型為

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

yij,zij≥0

，

(9)

xijk≥0,xijk∈+

，

(10)

式中：i,j∈{0,1,…,n}；k∈{1,2,…,K}。

目標(biāo)函數(shù)(1)為最小化車輛行駛總路程；約束條件(2)—(3)保證所有客戶點的需求均被滿足；式(4)—(5)確保離開配送中心時，車上沒有收集的貨物，當(dāng)車輛返回車場時，車上沒有待配送給客戶點的貨物；約束條件(6)表示車輛訪問某點的次數(shù)等于離開該點的次數(shù)；條件(7)表示每輛車僅離開配送中心1次，并最終返回配送中心；約束條件(8)保證車輛的實際裝載量不超過其最大裝載能力；式(9)—(10)表示變量約束。

也有學(xué)者描述目標(biāo)函數(shù)時，把最小化車輛使用數(shù)量作為第1層優(yōu)化目標(biāo)，最小化車輛行駛費用作為第2層優(yōu)化目標(biāo)，即

(11)

式中P1、P2(P1>>P2)與目標(biāo)規(guī)劃中的定義一樣，為優(yōu)先因子，是定性的概念，不賦予具體數(shù)值，只表示各目標(biāo)的優(yōu)先級。若固定費用和行駛費用都能準(zhǔn)確度量，則也可以用統(tǒng)一的費用量綱表示，轉(zhuǎn)化為單目標(biāo)優(yōu)化函數(shù)，直接進(jìn)行求和來比較優(yōu)劣，即

(12)

式中w1、w2分別表示單位車輛使用費和單位行駛距離行駛費用。Mitra[13]在研究VRPSPDP過程中給出一種假設(shè)，令w1=100，w2=0.1。Ai等[23]在考慮VRPSDP時，假設(shè)w1=100,w2=1。

VRPSPDP中對各客戶被拆分的次數(shù)無限制，可直接采用SVRPNDD數(shù)學(xué)模型。因為VRPDDP對客戶拆分方式及次數(shù)有限制，各客戶需求最多只能被拆分2次，所以需要在SVRPNDD模型中修改約束條件(10)為

0≤xijk≤2,xijk∈+,i,j∈{0,1,…,n},k∈{1,2,…,K}。

(13)

又因為VRPDDP中能夠被拆分的客戶只能是具有雙重需求的客戶，且被拆分的2次服務(wù)中，一次完成全部送貨需求，一次滿足所有取貨需求，所以SVRPNDD模型中的式(7)需要替換為

x0jk∈{0,1},j∈{0,1,…,n},k∈{1,2,…,K}，

(14)

xi0k∈{0,1},i∈{0,1,…,n},k∈{1,2,…,K}。

(15)

3.2 問題特性

縱觀已有SVRPNDD研究，主要研究重點為問題的算法求解，針對問題本質(zhì)特性的專項研究較少。問題特性的主要成果來自于王科峰等[8-10]。文獻(xiàn)[9]中指出，SDVRP是SVRPNDD中當(dāng)客戶點送貨和取貨2種需求之一為0時的特例，因此節(jié)點需求的雙重性帶來的問題結(jié)構(gòu)方面的改變，使得SVRPNDD比只有單一需求的SDVRP在固有性質(zhì)方面的研究更為困難。在研究SVRPNDD特性時，學(xué)者們通常會將其與SDVRP進(jìn)行比較。

3.2.1 計算復(fù)雜度

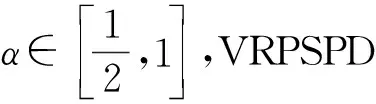
3.2.2 最優(yōu)解特性

問題最優(yōu)解特性是研究SVRPNDD的首要關(guān)鍵所在。雖然SVRPNDD是SDVRP的擴(kuò)展，但是，在最優(yōu)解的性質(zhì)方面兩者之間存在著明顯的差異。其原因是SVRPNDD中客戶點可以同時具有取貨及送貨2種需求，且2種需求相互制約。王科峰等[10]指出，目前直接研究SVRPNDD與SDVRP最優(yōu)解性質(zhì)的差異還存在困難。

已知的SDVRP重要最優(yōu)解特性見定理1、 2。

定理1[1]若距離矩陣滿足三角不等式， 則SDVRP最優(yōu)解中任意2條線路最多只存在一個公共點。

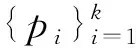
定理2[1]若距離矩陣滿足三角不等式， 則SDVRP最優(yōu)解中不存在k-拆分循環(huán)，k≥2。

定理3[25]若距離矩陣滿足三角不等式，則SDVRP最優(yōu)解中需求拆分點的個數(shù)少于路徑數(shù)。

王科峰等[8-9]研究了SVRPNDD是否具有與SDVRP相同的最優(yōu)解特性， 論證得出結(jié)論， 在SVRPNDD的最優(yōu)解中， 2條路徑間可能存在不止一個公共點， 與定理1不符。 同時VRPSPD中解的一條路徑中含有子回路的路徑相對于不含子回路的路徑可能會使行駛距離更短， 與定理3性質(zhì)相異。 Nagy等[22]也指出， VRPDDP最優(yōu)解不符合定理1及定理3， 且實際需求拆分點的個數(shù)沒有數(shù)量上限約束。

對比SDVRP最優(yōu)解特性，可得出SVRPNDD最優(yōu)解特性如下：1)若距離矩陣滿足三角不等式，則SVRPNDD最優(yōu)解中任意2條線路可存在多個公共點；2)若距離矩陣滿足三角不等式，則SVRPNDD最優(yōu)解中路徑中可能存在子環(huán)；3)若距離矩陣滿足三角不等式，則SDVRP最優(yōu)解中需求拆分點的個數(shù)無上限約束。

3.2.3 可還原性

王科峰等[8]研究了VRPSPD是否有與Archetti等[24-25]提出的SDVRP可還原性相類似的性質(zhì)，給出SVRPNDD可簡化性定義。

定義2[8]當(dāng)客戶點的取貨、送貨需求都大于或等于車輛最大裝載能力Q時，車輛滿載Q單位貨物，從車場出發(fā)直接到達(dá)該客戶點，在卸下車場運送來的Q單位貨物的同時，裝載需要運走的Q單位貨物，然后直接返回車場的運輸過程，稱之為直送(out-and-back)運輸操作。

定義3[8]若存在客戶點i的集貨、送貨需求均大于或等于車輛最大裝載能力Q，求得SVRPNDD的最優(yōu)解必須先通過對節(jié)點i進(jìn)行若干直送服務(wù)，直到該節(jié)點的收貨或送貨需求其中一個小于Q時直送服務(wù)停止。通過這種操作方式將問題簡化為求解一個新的SVRPNDD，則稱該SVRPNDD是可簡化的。

定義3與Archetti等[24-25]提出的SDVRP可還原性的定義方式相同， 王科峰等[8]經(jīng)論證提出， 如果問題距離矩陣對稱且滿足三角不等式， 則只有當(dāng)Q=1時，SVRPNDD是可簡化的。

3.2.4 成本節(jié)約

Archetti等[26]研究證明了客戶平均需求量與車輛裝載能力的關(guān)系是SDVRP成本節(jié)約的最大影響因素。 只有當(dāng)該因素滿足一定條件時， 才能使SDVRP獲得較大的成本節(jié)約。同時，SDVRP帶來的成本節(jié)約首先來源于需求可拆分所導(dǎo)致的車輛使用數(shù)的減少。雖然SVRPNDD與SDVRP在最優(yōu)解的性質(zhì)方面存在明顯的差異，但是在問題成本節(jié)約情況及特點方面存在許多共同之處。

Dror等[1]通過算例證明，當(dāng)客戶需求量與車輛裝載能力差異較小時，SDVRP的解較VRP并沒有太大的改進(jìn)。當(dāng)平均客戶需求量大于車輛裝載能力的10%時，需求拆分運輸將帶來明顯成本節(jié)約。該結(jié)論同樣適用于SVRPNDD。

Wang等[27]指出，當(dāng)平均客戶需求量為車輛最大裝載能力的50%，且需求量方差較小時，需求拆分運輸將帶來的最大運輸成本節(jié)約。該結(jié)論與Archetti等[26]的研究結(jié)論一致，即SDVRP帶來的成本節(jié)約情況受客戶需求量方差影響。不同的是，Wang等[27]指出SVRPNDD帶來的成本節(jié)約受客戶點的位置分布及聚類情況影響，而Archetti等[26]得到的研究結(jié)論與之相異，即SDVRP不受客戶點的位置分布影響。

綜上所述，SVRPNDD及SDVRP在成本節(jié)約方面的結(jié)論基本一致，兩者的比較如表2所示。

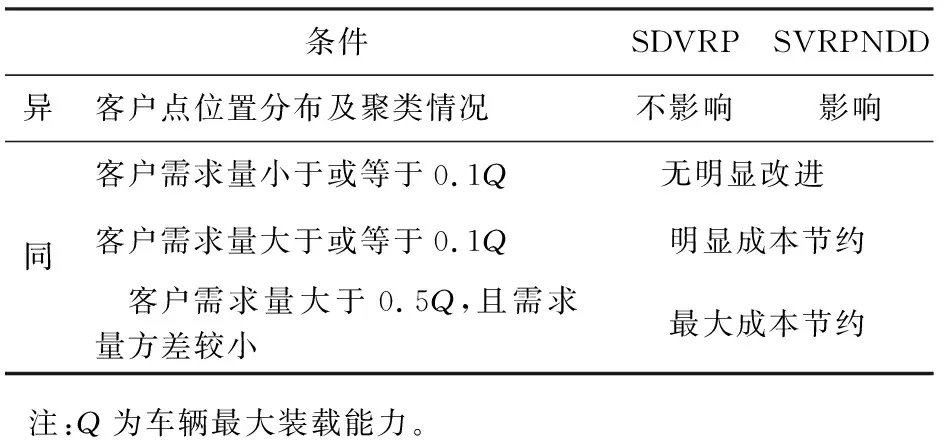
表2 需求可拆分的純送(取)貨車輛路徑問題(SDVRP)與需求可拆分的節(jié)點具有雙重需求的車輛路徑問題(SVRPNDD)在成本節(jié)約方面的比較

Nagy等[22]通過算例測試及分析發(fā)現(xiàn)，當(dāng)VRPDDP能夠得到較大成本節(jié)約時，往往發(fā)生在客戶2種需求量差異較大的情況。同時，文中進(jìn)一步分析總結(jié)得到最優(yōu)可能被拆分的客戶點一般具有如下特點，其中以1)尤其顯著： 1)客戶點鄰近配送中心(車場)； 2)客戶點某一需求量明顯較大； 3)客戶點位于某一較為密集的客戶點群中。

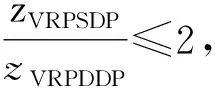
同時在文獻(xiàn)[22]中研究VRPDDP通過取送、送貨拆分運輸?shù)牟僮鞣绞浇o對應(yīng)VRPSDP能夠得到最大的成本節(jié)約，給出定理4，與Archetti等[28]針對SDVRP的研究結(jié)論相符。

3.3 求解算法

已知SVRPNDD是NP-難問題，高效的求解算法研究是解決該問題的重要途徑。已有研究中，大部分學(xué)者采用啟發(fā)式算法，原因是規(guī)模較大的問題中，即使在VRPNDD模型(需求不可拆分的運輸方式)中能夠輕松求解，相應(yīng)的SVRPNDD模型也不一定能夠求得問題最優(yōu)解。這是因為各客戶點被拆分的次數(shù)在SVRPNDD模型中是決策變量，所以會使整數(shù)規(guī)劃模型產(chǎn)生巨大的不完整空隙。

精確算法只能求解小規(guī)模的NP-難問題，已有SVRPNDD的求解算法研究均采用啟發(fā)式算法。早期的算法研究主要以構(gòu)造啟發(fā)式算法為主，特別是元啟發(fā)式算法(metahueristics，也稱智能優(yōu)化算法、超啟發(fā)式算法、亞啟發(fā)式算法、通用啟發(fā)式算法等)及混合啟發(fā)式算法已成為求解SVRPNDD的主要研究方向。

構(gòu)造啟發(fā)式算法的研究主要出現(xiàn)在該領(lǐng)域研究早期(2005—2012年)[4,11,18-19,29-30]，其中主要通過先聚類后路徑(cluster-first-route-second)方法求解。在聚類階段，學(xué)者們通過各種貪婪算法生成初始路徑方案，再結(jié)合最短路及智能算法對解進(jìn)行優(yōu)化。

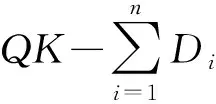
在路徑優(yōu)化階段，Mitra[13]與楊亞璪等[29]采用的是最短路徑法，而大多數(shù)學(xué)者則是采用智能算法進(jìn)行優(yōu)化，其中以禁忌搜索算法的應(yīng)用居多[20-22,31]。除此外，還包括蟻群算法[32-33]、競爭決策算法[30,34]、模擬退火算法[31]及平行算法[35]等。

4 結(jié)語

GPDP的研究對物流配送路徑的確定具有重要意義及應(yīng)用前景，特別是在客戶點可能同時具有取貨及送貨2種需求的情況下，即VRPNDD問題類型。允許對客戶需求進(jìn)行拆分，由多輛車共同運輸或由同一輛車多次運輸?shù)牟僮鞣绞剑軌蛟谧畲蟪潭忍岣咂骄囕v裝載率，充分利用車輛裝載能力的同時，降低車輛行駛成本，帶來整體運輸成本節(jié)約。

近幾年關(guān)于SVRPNDD的研究得到了一些富有意義的研究成果，但是無論是在理論還是求解算法方面，在深度及廣度上仍有較大的研究及拓展空間。主要表現(xiàn)在如下2個方面：

1)相對于SDVRP，SVRPNDD在問題性質(zhì)研究方面仍有很大的探索空間。目前已有的對SVRPNDD性質(zhì)的研究結(jié)論大部分仍為猜測及推論，需要進(jìn)一步論證和分析，例如SVRPNDD的最優(yōu)解特征、成本節(jié)約情況等。

2)在實際物流實例中，客戶更加傾向于較少的訪問次數(shù)，或多種類貨物多車型混合運輸?shù)龋粼赩RPSPD中考慮客戶最大訪問次數(shù)、多種貨物或多車型混合運輸?shù)雀郊蛹s束條件，將增大問題的復(fù)雜程度。同時，附加條件將限制可行解的數(shù)量，因此需要研究設(shè)計性能更好的求解算法。