電動機中反電動勢模型的建立與釋疑*

吳廣國

(北京景山學校 北京 100006)

張思宇

(北京市東城區教師研修中心 北京 100009)

黃琭琰 鄒斌

(中央民族大學理學院 北京 100081)

1 問題來源

人教版普通高中《物理·選修3-2》的“法拉第電磁感應定律”一節中講到反電動勢．教材中給出如圖1所示的直流電動機，并提出了這樣的問題：處于磁場中的線圈轉動，會使得線圈中產生感應電動勢．那么，線圈中的感應電動勢對電源產生的電流是起了加強作用還是減弱作用呢？是推動還是阻礙線圈的轉動呢？[1]

圖1 直流電動機的模型和側面圖[2]

由圖1可知，直流電動機工作時，當線圈處于圖中位置處，ab與cd均切割磁感線，根據右手定則，該兩部分動生電動勢串聯在電路中，與原回路中電源相反，使得原電源產生的電流減小，并阻礙了線圈的轉動．

電動機工作時，線圈中也會產生感應電動勢，線圈產生的感應電動勢對電源電動勢總是起反作用，因此通常把這個電動勢稱為反電動勢．它的作用是阻礙線圈的轉動．如果電動機工作中發生突發情況使得機械阻力過大，導致電動機停止轉動，這時反電動勢為零，線圈就等于直接短接在電源兩端；而一般線圈電阻都很小，這時通過其的電流很大，長時間的大電流很容易把線圈燒毀．因此，當發現電動機由于機械故障停轉時，應立刻切斷電源，維修檢查．

如圖2通過實驗研究直流電動機轉動過程中，回路中電流隨時間變化情況．電流的測量用Vernier電流傳感器，每秒鐘測樣200次，通過I-t圖像可以看出，當閉合開關電動機開始轉動時，電流較大等于0.37 A，隨著電動機轉速越來越高，反向電動勢越來越大，從而消弱了電源產生的電流．在該實驗中，電動機處于空載狀態，電動機轉速較高，從而產生較大的反向電動勢，電動機穩定轉動后，回路中的實際電流很小等于0.024 A．在5 s時刻后用手去摩擦電動機阻礙電動機的轉動，直到電動機停止轉動，實驗圖像和數據表明，當降低轉速時，反向電動勢減小，回路中電流增大，當電動機停止轉動時，回路中電流約等于0.404 A．

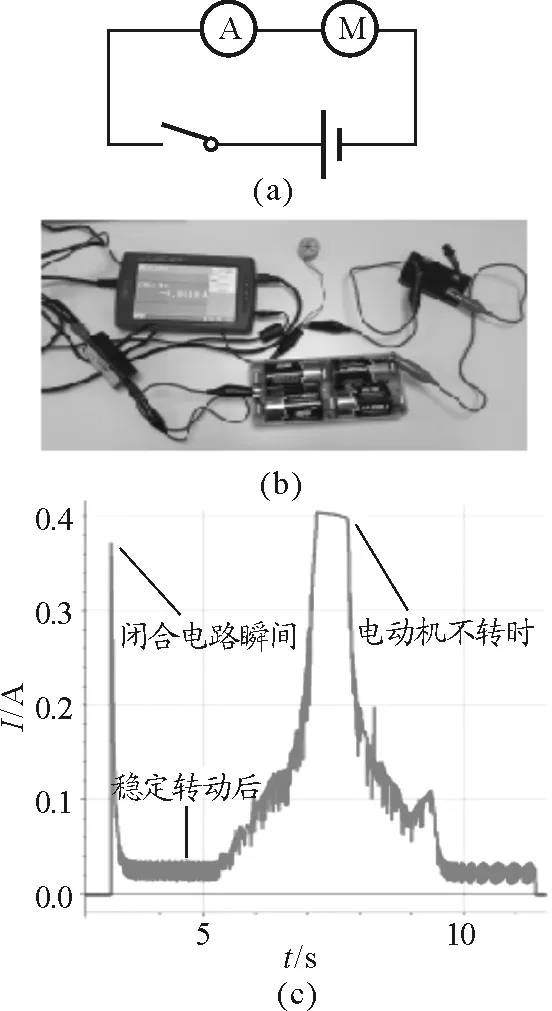
圖2 利用傳感器觀察電動機啟動過程中電流的變化情況

2 電動機中反電動勢模型

在直流電動機中，無論是圖1電動機中線圈的切割磁感線產生的反電動勢，還是如圖3所示運動的導體棒切割磁感線產生的反電動勢原理都是相同的．如圖3所示，足夠長的平行光滑導軌PQ，MN相距l，處在同一水平面中，磁感應強度B的勻強磁場豎直向下穿過導軌面．橫跨在導軌上的金屬棒ab靜止，質量為m，電阻為R，導軌電阻不計．導軌間通過開關S將電動勢為E，內電阻r的電池接在M，P兩端，試分析開關S剛閉合的瞬間和后續過程中，金屬棒ab的加速度、速度如何變化？導體棒中的電流如何變化？

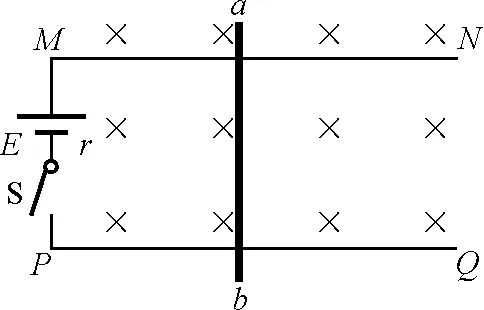
圖3 導體棒ab運動切割磁感線產生反電動勢

開關S閉合瞬間，導體棒的速度為零

BIl=ma

求得此時加速度為最大值

(1)

設后續任意時刻t,導體棒ab的速度為v(t)，則ab棒切割磁感線產生反電動勢，電路圖變為圖4所示．

圖4 ab棒充當反電動勢

E-Blv(t)=I(t)(R+r)

(2)

(3)

安培力使導體棒產生的加速度可由牛頓第二定律得

(4)

所以

(5)

解該微分方程，得

(6)

(7)

(8)

通過以上v(t)、a(t)、I(t) 3個物理量的表達式，可以定性地畫出v(t)、a(t)、I(t)函數圖像如圖5所示．

圖5 導體棒v-t，a-t和I-t圖像

3 從微觀角度理解電動機的工作原理

2017年高考北京物理卷中第24題考查了電動機的問題，如圖6所示，ab棒充當電動機中導體棒，導體棒ab最后通過定滑輪拉動重物勻速直線運動．軌道端點MP間接有直流電源，導體棒ab通過滑輪勻速提升重物，電路中的電流為I.

(1)求在Δt時間內，圖6“電動機”輸出的機械能；

(2)從微觀角度看，導體棒ab中的自由電荷所受洛倫茲力在上述能量轉化中起著重要作用．為了方便，可認為導體棒中的自由電荷為正電荷．

我們知道，洛倫茲力對運動電荷不做功．那么，導體棒ab中的自由電荷所受洛倫茲力是如何在能量轉化過程中起到作用的呢？請以圖6“電動機”為例，通過計算分析說明．

圖6 2017年高考北京第24題“電動機”模型

解析：

(1)“電動機”輸出的機械能轉化為重物重力勢能的增加

ΔEp=mgvΔt

mg=BIl

所以 ΔEp=BIlvΔt

(9)

拓展：其實該“電動機”的輸出功率P出=Iε反，對整個回路，由閉合電路歐姆定律有

(E-ε反)=I(R+r)

等式兩邊同時乘以電流I，得

I(E-ε反)=I2(R+r)

移項得IE=I2(R+r)+Iε反

(10)

由能量守恒定律可知，電源E消耗的電功率，一部分為電路中ab棒電阻R與電源內阻r產生焦耳熱功率，其他為提升重物的機械輸出功率，即P出=Iε反．

(2)如圖7所示為電動機中導體棒ab中載流子所受洛倫茲力的情況．設導體棒橫截面積為S，單位體積內自由電荷的數目為n，自由電荷電荷量為q，自由電荷沿桿方向速率為vy，則

垂直于導體棒方向(x方向)洛倫茲力分力為

Fx=Bqvy

沿導體棒方向(y方向)洛倫茲力分力為

Fy=Bqv

因此，得到洛倫茲力x，y方向的分力所做功

Wx=nSlFxvΔt=

nqSvyBlvΔt=BIlvΔt

(11)

Wy=-nSlFyvyΔt=

-nqSvyBlvΔt=-BIlvΔt

(12)

綜上，洛倫茲力不做功，但沿導體棒方向的洛倫茲力分力Fy做負功，阻礙自由電荷運動，消耗電能；垂直導體棒方向洛倫茲力分力Fx做正功，推動導體棒運動，使得機械能增加．從微觀上說，雖然洛倫茲力對運動電荷不做功，但在宏觀上看，運動的自由電荷借助于洛倫茲力將電能轉化為機械能[4]．

圖7 電動機導體棒ab中載流子所受洛倫茲力情況

疑惑1：為何“沿桿方向洛倫茲力分力Fy做負功是在消耗電能”？

從功能關系角度來看，“垂直導體棒方向洛倫茲力分力Fx做正功，推動導體棒運動，使桿的機械能增加”，這個結論很好理解，因為根據動能定理：合外力對物體做正功，其作用是使質點的動能增加，因此判斷出Fx的功為正值，即可知其作用是使電荷的動能增加．但是“沿導體棒方向的洛倫茲力分力Fy做負功，阻礙自由電荷運動，消耗電能”，這個結論就不容易找到依據了．如果根據動能定理，通過Fy對電荷做負功，只能得出使電荷的動能減少的結論；如果從“靜電力和非靜電力做功”的角度來看，電荷在電路中的電池(E,r)提供的靜電力作用下沿桿從a向b運動，若將洛倫茲力分力Fy視為“非靜電力”，此“非靜電力”正在克服靜電力做功，而克服靜電力做功的結果應該是使電勢能增加．到底如何解釋Fy做負功所起的作用呢？可以結合圖4所示的宏觀模型來解釋Fy的作用：確實可以將Fy視為“非靜電力”，但它是電路中另一個電源，即圖4中由于切割磁感線產生反電動勢的ab棒這個電源的“非靜電力”，它的作用是克服靜電力做功使ab棒這個電源的電勢能增加，而非使電路中電池的電勢能增加[5]．從整個電路的角度來看，正是由于這個反電動勢的存在，使圖4中由電池所提供的電能沒有全部轉化為內能(與沒有反電動勢時相比)，而是通過Fy做功產生反電動勢使電流減小的途徑將本來也會變為內能的一部分電能“接住”，再通過Fx做正功轉化為機械能．這就從微觀解釋了是通過反電動勢完成了電能到機械能的轉化．

疑惑2：所有載流子在x方向上的洛倫茲力的合力∑Fxi，宏觀上表現為導體棒受到的安培力，洛倫茲力是作用在導體棒中的載流子，如何就體現為作用在導體棒的安培力呢？

拓展釋疑：以靜止的載流導體為例，如圖8所示．

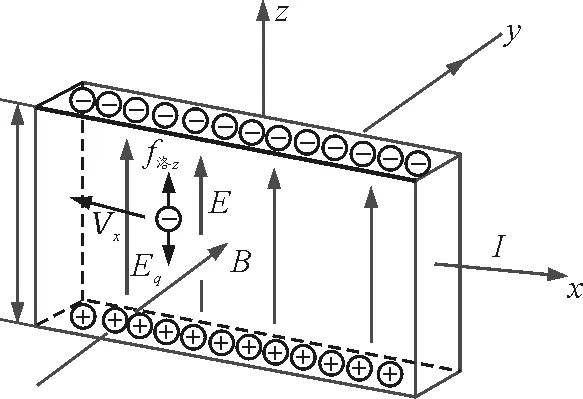
圖8 靜止載流導體霍爾效應圖

如圖8所示為一載流導體，載流導體置于勻強磁場B中，載流導體中所有定向運動的電子都受到洛倫茲力f洛作用，f洛=-ev×B,沿z方向.這導致導體的上表面出現負電荷堆積，而在下表面出現正電荷的堆積，結果與霍爾效應一樣，載流導體產生了沿+z方向的電勢差.一段時間后，電場力與洛倫茲力平衡，此時電子運動情況與外磁場B不存在時相同(沿-x方向運動)；不同在于載流導體內部出現了橫向電場[6].而對定向移動的電子進行受力分析可知，電場力和洛倫茲力受力平衡。由穩恒的電場力必須遵從牛頓第三定律可知，電子將給載流導體上下表面上聚集的電荷施加沿+z軸的反作用力，這個反作用力與外磁場對運動電子施加的沿+z軸的洛倫茲力等大反向.綜上，外磁場作用在運動電子上的洛倫茲力雖不做功，但能通過橫向電場的中間作用，表現為外磁場推動載流導體的安培力做功[7].因此，安培力是洛倫茲力的宏觀表現.