平行光垂直入射光柵面的調節方法探討

李子良

[中國礦業大學(北京)理學院 北京 100083]

陸丁

(北京交通大學附屬中學 北京 100081)

根據光柵的衍射現象，利用分光計測量光柵常數是普通物理實驗中的重要內容[1～3]．通常光柵常數的測量是利用平行光垂直入射光柵時的光柵方程實現的，所以操作上要求平行光是垂直入射到光柵上的．就平行光非垂直入射對測量結果的影響，文獻[4]討論了光柵以3種不同方式傾斜時對光譜波長測量的影響，文獻[5]則證明了光柵以與小平臺接觸的長邊為軸有旋轉時對光柵常數測量的影響可以忽略．但是，光柵以中心刻線方向為軸有旋轉時對光柵常數測量的影響是不能忽略的．此時，可以用自準直法調節光柵實現平行光垂直入射到光柵上[6]，還可以通過調節光柵使正負一級光譜的偏向角之差達到一定范圍來實現．由于學生在光柵衍射實驗之前做過測量三棱鏡折射率的實驗，對自準直法已經非常熟悉，所以第二種方法更能拓寬學生的知識面，提高學生的實驗技能，加深學生對光柵衍射實驗的理解．下面主要討論該操作方法．

1 調節方法

首先，打開光源預熱并對分光計進行必要的調節[1,2]．然后，在分光計載物臺上目測放置光柵使光柵面垂直于平行光管光軸，分別測量出零級光譜(中央眀紋)及其左右兩側的負正k級光譜的方位．根據測量結果計算出正負k級光譜所對應的偏向角(正負k級光譜偏離入射光的角度)，并判斷它們的大小．如果正k級光譜的偏向角大，那么就逆時針轉動載物臺(從俯視的角度觀察)，如果負k級的大，就順時針轉動載物臺．之后，再次測量正負k級光譜的方位，計算相應偏向角之差，判斷是否達到了垂直入射的標準．如果還不滿足，則重復上述的操作技巧，直到調節到平行光垂直入射到光柵為止．另外，需要注意判斷平行光是否垂直入射到光柵上的標準是與測量精度的要求有關的．通常實驗教材里認為平行光垂直入射到光柵上的判斷標準是正負一級光譜的偏向角之差不超過2′[1,2]．事實上，這一標準所對應的測量精度是非常高的，在實際教學中，學生操作起來并不容易．因此，在測量精度要求不高的情況下可以適當放寬判斷標準，這既能讓學生掌握操作方法，又能高效地完成實驗．

2 理論證明

該部分將通過給出正負k級光譜對應的偏向角之差與斜入射角度的關系，從理論上證明平行光垂直入射光柵的調節方法的合理性．

首先，考慮入射角θ比較小時，如圖1所示，φ+和φ-分別為正負k級光譜與光柵法線的夾角．此時，φ+和φ-分別位于光柵法線上下兩側，正負k級光譜對應的偏向角分別為φ+-θ和φ-+θ，則由斜入射光柵方程[3]

可得正負k級光譜對應的偏向角之差為

F1(θ)=φ+-θ-(φ-+θ)=φ+-φ--2θ=

其中λ為實驗室所用光源的光波波長，d為光柵常數．

圖1 斜入射角度θ 較小時，光柵衍射示意圖

當入射角θ比較大時，如圖2所示，φ+和φ-都在光柵法線上側，正負k級光譜對應的偏向角分別為φ+-θ和θ-φ-，則由斜入射光柵方程[3]

圖2 斜入射角度θ 較大時，光柵衍射示意圖

可得正負k級光譜對應的偏向角之差為

F2(θ)=φ+-θ-(θ-φ-)=φ++φ--2θ=

由上述討論可知，對于任意入射角θ，正負k級光譜對應的偏向角之差為

值得注意的是，雖然上述討論針對的是平行光斜向上入射到光柵面的情況，但是根據對稱性對于平行光斜向下入射的情況也可得到相同的規律，只不過F(θ)表示的是負正k級光譜對應的偏向角之差．

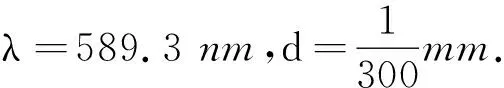
圖3 斜入射時，正負k級譜線的偏向角之差F(θ)隨斜入射角度θ的變化，其中

3 誤差分析

根據垂直入射時的光柵方程dsinφ=±kλ,通過測量正負k級光譜的衍射角φ，即可求出光柵常數d．如果平行光是以入射角θ斜入射到光柵上的，而實驗中仍然使用垂直入射時的光柵方程求解光柵常數，那么結果為

(1)

圖4分析了當平行光非垂直入射光柵時所導致的相對誤差隨正負k級光譜對應的偏向角之差F(θ)的關系．從圖中可以看到，相對誤差隨F(θ)的增加而增大，對于相同的F(θ)值，由高級次光譜求得的光柵常數誤差較小，而由較低級次光譜求得的誤差較大．因此，從誤差分析來看選取三級光譜調節測量時會比一級光譜效果要好．但是，在實際的教學過程中還要綜合考慮測量精度要求和操作的難易程度來確定選取哪一級光譜進行調節測量．

圖4 光柵常數的相對誤差隨正負k級譜線的偏向角之差的變化，其中

當選取一級光譜調節測量時，如果使正負一級光譜對應的偏向角之差F(θ)=2′，則由一級光譜得到的光柵常數相對誤差約為0.017%．由此可以看出，此時光柵常數的測量誤差已經非常小，完全可以忽略斜入射的影響，即認為平行光是垂直入射到光柵上的．當選取三級光譜調節測量時，如果要達到上述測量精度，那么需要調節光柵位置使正負三級光譜對應的偏向角之差達到21′．

如果對光柵常數的測量精度要求更高，那么就要要求正負級次光譜對應的偏向角之差更小．但是，對于一級光譜，當偏向角之差降到1′時，就達到了分光計的儀器誤差范圍，由正負一級光譜得到的光柵常數的相對誤差約為0.004 2%已達最小，無法繼續提高測量精度．而此時，對于三級光譜，達到相同的測量精度時，偏向角之差約為10′，還可以繼續提高光柵常數的測量精度．所以，對于光柵常數測量精度要求非常高時，選取三級光譜調節測量更合適．但是，在物理實驗教學中，測量精度的要求并不是很高，又考慮到選取三級光譜進行調節測量時光譜的強度較弱不容易被觀察、光譜的級次較高不容易被確定等因素的影響，所以選取一級光譜調節測量更合適．總之，在測量精度允許的范圍內，選取一級光譜進行調節會更加簡便易行，利于學生掌握．

如果實驗中要求光柵常數的測量相對誤差小于0.5%，那么對正負一級光譜對應的偏向角之差的要求可以放寬到10′．以一級光譜作為研究對象，從圖3可以看到F(θ)=10′時對應的斜入射角θ≈5°9′．在這種情況下斜入射角已經很大，眼睛就能觀察出來，通常目測放置光柵使光柵面盡量與平行光管光軸垂直就能滿足條件，所以光柵實驗中測量精度要求不是很高時，是比較容易調到平行光垂直入射光柵的．另外，此處的討論是基于鈉黃光波長的，又由公式 (1) 可以看出隨著光波波長的增加測量誤差會更小，所以增加光源的光波波長是可以有效減小斜入射對光柵常數測量的影響的．

上述討論中計算光柵常數的公式 (2) 是對由正負k級光譜的偏向角計算的光柵常數求平均得到的．實驗教材中[1,2]通常強調為了提高精度使用的是公式

(2)

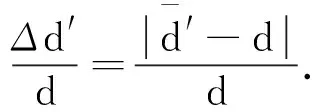
4 結束語

光柵衍射實驗可以通過測量正負一級光譜的偏向角判斷平行光是否垂直入射光柵，進而調節光柵位置以滿足垂直入射到要求．具體調節技巧得到了理論上的證明．另外，通過分析斜入射對光柵常數測量造成的誤差，發現部分實驗教材中指出的調節光柵使正負一級光譜對應的偏向角不超過2′即認為達到垂直入射對精度的要求已經非常高了[1,2]．一般精度要求不是很高的情況下，可以把偏向角之差的要求放寬到10′，這在實驗教學中既能讓學生掌握思想和方法，又能節省操作時間，提高實驗效率．當然，如果實驗室光源的光波波長較短的話，正負一級光譜對應的偏向角之差還要要求更小一些．