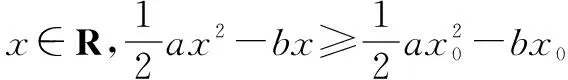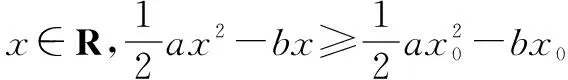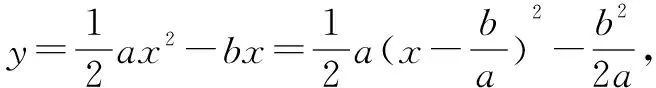盤點高考中的二次函數

付一駿

(河南省民權縣高級中學 476800)

一、二次函數的圖象

整合二次函數的圖象信息通常有以下幾點:開口方向(向上或向下)、對稱軸的位置、頂點(特別是與坐標軸的交點)坐標、最值的大小等.

例1 設abc>0,二次函數f(x)=ax2+bx+c的圖象可能是( ).

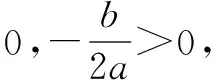
二、二次函數的定義域

二次函數的定義域是一個自變量的取值區間,對于值域等性質的影響也是客觀存在的,不可小視.

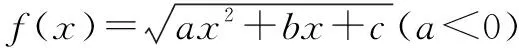
A.-2 B.-4 D.-8 D.不能確定

三、二次函數的值域

值域要在單調區間,以及對稱軸,相應的定義域內結合圖象來分析.

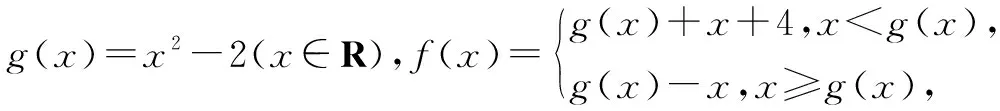
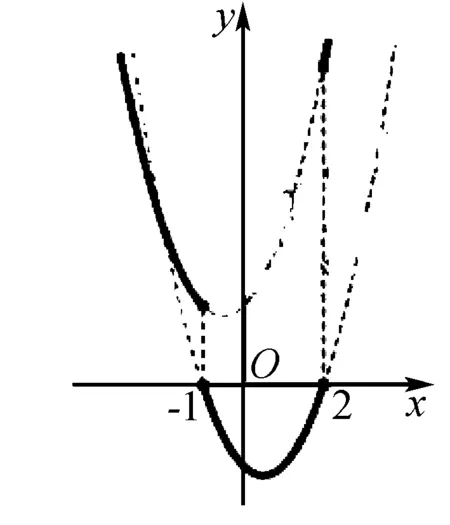
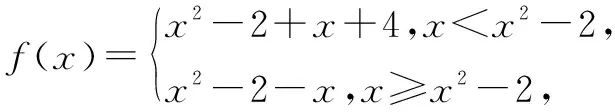
四、二次函數的解析式

二次函數的對應法則有頂點式、零點式、一般式等三種,注意三者之間的相互轉化.

例4 若f(x)和g(x)都是定義在實數集R上的函數,且方程xf[g(x)]=0有實數解,則g[f(x)]不可能是( ).

解設x0為方程x-f[g(x)]=0的一個實根,則f[g(x0)]=x0.設g(x0)=y0,則f(y0)=x0,所以g(x0)=g[f(y0)]=y0,即g[f(y0)]-y0=0.這說明方程x-f[g(x)]=0至少有一個實根y0,于是有結論:定義在R上的函數f(x)與g(x),若x0是方程f[g(x)]=x的實數解,則g(x0)必是方程g[f(x)]=x的實數解.

五、二次函數的零點

一般情況下,可通過畫函數圖象、判斷特殊點的函數值的情況,布列不等式(組)來解決問題.

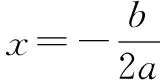
A. {1,2} B. {1,4}

C. {1,2,3,4} D. {1,4,16,64}

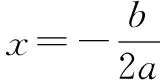
六、二次函數的最值

二次函數的最大值和最小值一般在對應圖象的頂點或區間端點處取得.因此,關于對稱軸與區間的相互位置關系的討論往往成為解決二次函數在閉區間上的最值問題的關鍵,通常需要考察“一軸四點”,即對稱軸、頂點、區間兩端點和區間中點.

例6 已知a>0,則x0滿足關于x的方程ax=b的充要條件是( ).