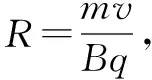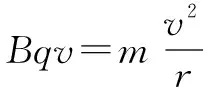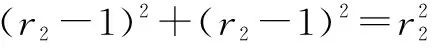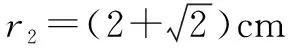大量粒子運動的臨界問題

陶漢斌

(浙江金華第一中學 321015)

浙江省的選考物理試題中常出現“大量粒子”的運動問題，由于這類問題涉及的研究對象是大量的粒子，而我們不可能對大量粒子中的每一個粒子都進行分析，那么我們應該如何選取恰當的粒子做為研究對象呢？從粒子源射出的大量粒子有自己的個性與共性問題，比如大量粒子的速率相同而方向不同，比如大量粒子的速度方向相同而速率大小不同.同學們要根據運動的臨界條件，恰當地選取“臨界”粒子，利用“臨界”粒子進行分析使問題變得簡潔明了、形象生動.

例1如圖1所示，x軸上方存在垂直紙面向外的勻強磁場，坐標原點處有一正離子源，單位時間在xOy平面內發射n0個速率均為v的離子，分布在y軸兩側各為θ的范圍內.在x軸上放置長度為L的離子收集板，其右端點距坐標原點的距離為2L，當磁感應強度為B0時，沿y軸正方向入射的離子，恰好打在收集板的右端點.整個裝置處于真空中，不計重力，不考慮離子間的碰撞，忽略離子間相互作用.

(2)如果發射的離子被收集板全部收集，求θ的最大值；

(3)假設離子到達x軸時沿x軸均勻分布.當θ=37°，磁感應強度在B0≤B≤3B0的區間取不同值時，求單位時間內收集板收集到的離子數n與磁感應強度B之間的關系.(不計離子在磁場中運動的時間)

解析正離子源射出的離子速率是相同的，因此它們在磁場中都做相同半徑的勻速圓周運動，只是轉過的圓心角不同，也就是經歷的圓弧長度不同.那么分布在y軸兩側各為θ的范圍內大量粒子，哪個是臨界粒子呢？我們知道圓周中最長的弦長是直徑，因此沿y軸正方向射入的粒子是打到收集板上最遠的臨界粒子，而沿y軸兩側以θ角射入的兩個離子也是臨界粒子，因為這兩個離子的弦長是最短的，是打到收集板上最近的臨界粒子，其中一個是優弧，另一個是劣弧.具體解答如下：

(1)對帶電粒子的圓周運動

而沿y軸正方向入射粒子軌跡為半圓R=L

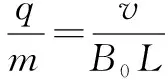
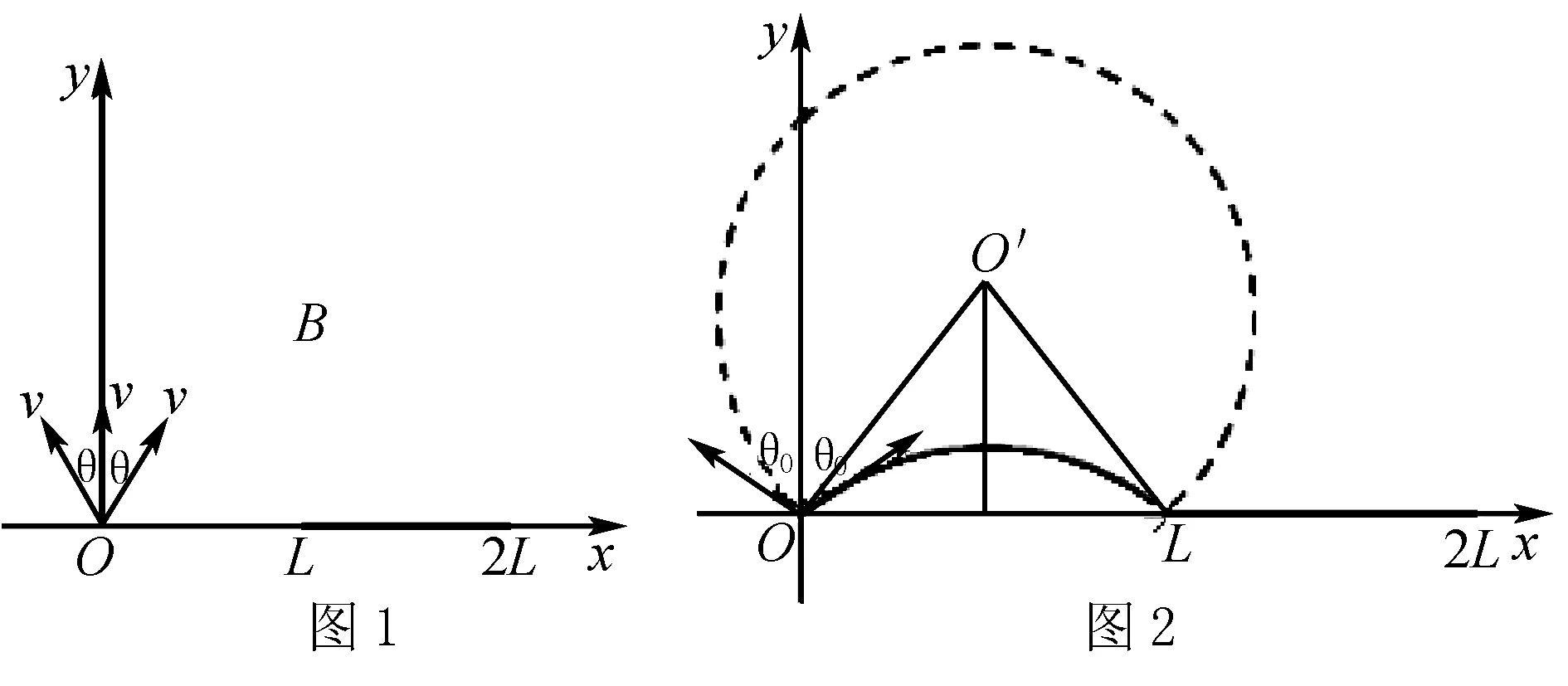
(2)選取與y軸正方向夾角相同的向左和向右2個粒子為臨界粒子.當粒子恰好達到收集板最左端時，θ達到最大，粒子軌跡如圖2所示

由圖中幾何關系得2Rcosθm=L=R

因此可得θmax=600

(3)以沿y軸正方向入射的粒子為臨界粒子，打在x軸上距離原點最遠的距離為2R.

沿與y軸正方向馬θ=37°入射的臨界粒子，打在x軸上距離原點最近距離為2Rcosθ=1.6R

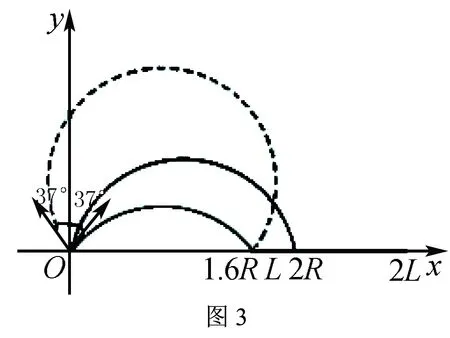
也就是說粒子打在x軸上的區間為1.6R～2R，而在x軸上吸收板的區間為L～2L，如圖3所示.若全部收集到離子時的最小半徑為R1，則有

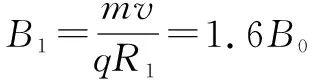
當B0≤B≤1.6B0時收集板上收集到的離子數n1=n0

若恰好收集不到離子時的半徑為R2，則有2R2=L

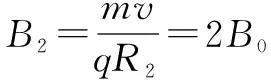
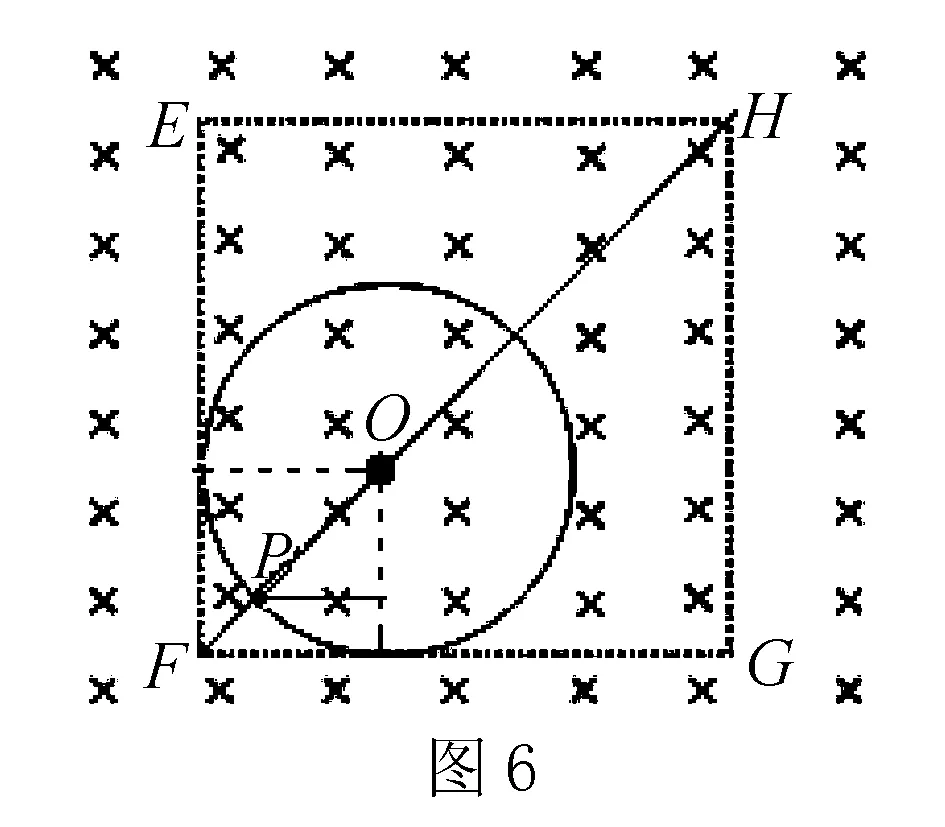
當2B0

例2 如圖4所示，在B=0.1 T的勻強磁場中畫出 邊長為L=8 cm的正方形EFGH，內有一點p，它與EF和FG的距離均為1 cm，在P點有一個發射正離子的裝置，能夠連續不斷地向紙面內的各個方向發射出速率不同的正離子，離子的質量為1.0×10-14kg，電荷量為1.0×10-5C，離子的重力不計，不考慮離子之間的相互作用.(計算結果可保留根號)

(1)速率在什么范圍內的離子不可能射出正方形區域?

(2)速率為1×106m/s的離子在紙面上向各個方向均勻發射，求不會射出正方形區域的離子與能射出正方形區域的離子的個數之比.

(3)速率大于多少的離子將全部射出正方形區域？

解析這些大量粒子的速率不同，在磁場中運動的軌道半徑也不同，但這些粒子是從同一個點P出發的.在粒子做圓周運動的過程中，弦長最長的是直徑.具體解法如下：

(1)P到正方形邊界最近的距離為1 cm，選取直徑為1 cm向左或向上的粒子為臨界粒子，臨界條件是粒子運動的軌跡剛好與邊界相切.

解得v=5×105m/s

因此只要v<5×105m/s離子不可能射出正方形區域.

(2)速率為v1=1×106m/s的離子在磁場運動的軌道半徑為r1=1.0 cm

選取向下和向右運動的粒子為臨界粒子，此粒子的臨界條件是運動軌跡恰好與邊界相切，如圖5所示.兩個臨界粒子速度間角度為900，在360°的整個空間平面內，粒子速度從水平向右順時針轉到豎直向下的90°范圍內的粒子將不會射出磁場區域，而再從豎直向下順時針轉270°范圍內的粒子將射出磁場區域，因此，不會射出正方形區域的離子與能射出正方形區域的離子的個數之比為1比3.

上文中的兩個案例對大量粒子的運動問題進行了分析闡述，求解大量粒子的運動問題時，根據臨界條件恰當地選取臨界粒子，搞清楚什么物理事件，物理事件的臨界條件是什么.

一旦找到了滿足臨界條件的臨界粒子，就可以利用“臨界”粒子進行分析使問題變得簡潔明了、形象生動.