笛卡爾方法論及解析思想在平面幾何中的應(yīng)用

李 旭

(遼寧省盤錦市遼河油田第三高級(jí)中學(xué) 124000)

方法論思想最初由法國(guó)數(shù)學(xué)家笛卡爾在《談?wù)劮椒ā芬粫刑岢?在此摘取其中四條規(guī)則，作為本文討論的核心.分別是：1.凡是我沒有明確地認(rèn)識(shí)到的東西，我決不把它當(dāng)成真的接受；2.把我所審查的每一個(gè)難題按照可能和必要的程度分成若干部分，以便一一妥為解決；3.按次序進(jìn)行我的思考，從最簡(jiǎn)單、最容易認(rèn)識(shí)的對(duì)象開始，一點(diǎn)一點(diǎn)逐步上升，直到認(rèn)識(shí)最復(fù)雜的對(duì)象；4.在任何情況之下，都要盡量全面地考察，盡量普遍地復(fù)查，做到確信毫無遺漏.結(jié)合高中考生所面對(duì)的問題，對(duì)以上四條簡(jiǎn)單說明.1.解決問題時(shí)只可用已知的定義、定理，不可盲目造定理；2.將完整復(fù)雜問題拆分成若干簡(jiǎn)單問題，逐個(gè)解決；3.分析條件，理清各對(duì)象之間的層級(jí)關(guān)系，最終將各低層級(jí)對(duì)象聯(lián)系在一起解出題目；4.不可遺漏條件，檢查.以下題為例，將上述理論思想用于實(shí)踐.

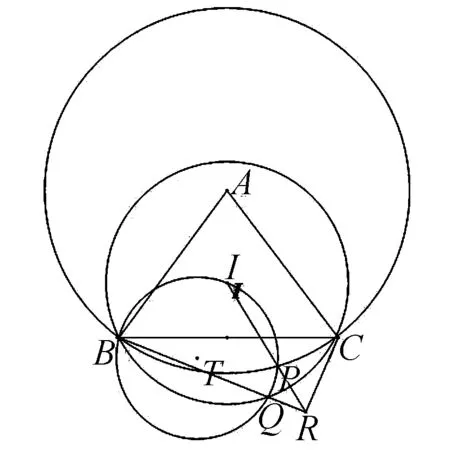
題目如圖，在△ABC中，AB=AC，I為△ABC的內(nèi)心.以AB為半徑作圓A，以IB為半徑作圓I，過點(diǎn)B，I的圓與圓A、圓I分別交于點(diǎn)P、Q(不同于點(diǎn)B).設(shè)IP與BQ交于點(diǎn)R.證明：BR⊥CR.(2017年全國(guó)高中數(shù)學(xué)聯(lián)合競(jìng)賽加試第一題)

解析題干中所涉及各幾何元素父對(duì)象、子對(duì)象關(guān)系如下圖：

證明思路是：將要證明的命題，轉(zhuǎn)換為各路徑對(duì)應(yīng)的簡(jiǎn)單問題，利用解析知識(shí)逐個(gè)解決，最終利用斜率證得垂直關(guān)系.

解法如下：

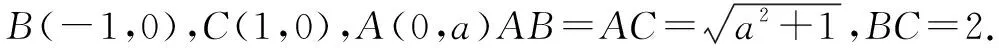
⊙A:x2+(y-a)2=a2+1;

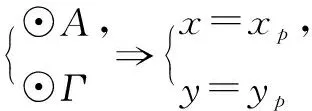
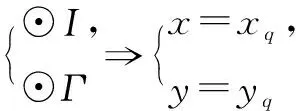
B(-1,0),Q(xq,yq),I(0,yi),P(xp,yp),

lBQ∩lIP=R,R(xr,yr),

在計(jì)算過程中， 參數(shù)為點(diǎn)A縱坐標(biāo)a與圓Γ圓心橫坐標(biāo)xt，將其代入到方程組解中，得

經(jīng)化簡(jiǎn)，kBR·kCR=-1,得證.

此解法與傳統(tǒng)幾何方法相比，思路較為簡(jiǎn)單清晰，但對(duì)應(yīng)計(jì)算量較大，需要扎實(shí)的運(yùn)算基礎(chǔ).兩種解法各有利弊，在解題時(shí)可根據(jù)自身情況選擇方案.