如何用高等數學知識解初等數學題

關 鍵

(黑龍江省大慶四中 163000)

數學知識是相通的，許多高等數學中的解題方法可直接用來求解初等數學題，使我們能快速地確定解題思路，進而能夠找出更簡捷的解題方法.因此作為高中的數學教師在進行教學時，可以教會學生一些高等數學的解題方法，以幫助他們能夠用多種方法解決初等數學問題，同時還可以激發學生學習數學的積極性，提高他們解決實際問題的能力.

一、高等數學與初等數學之間的聯系

初等數學是高等數學的基礎，高等數學是由初等數學發展而來的.因此只有先學習和掌握了初等數學知識才能夠學會和運用高等數學知識.同理，學習高等數學知識有助于加深對初等數學知識的理解，進一步提高學生解決問題的能力.如在研究函數的增減性以及求極值和最值等一些特性時，具有較大的局限性.如果用高等數學知識中的極限、級數和導數就可以很好地解決函數的特性問題.有些題可以選擇用高等數學知識和初等數學知識同時解決，通過對比，提高學生對這兩種方法的理解和認知水平，同時還可以激發學生的學習興趣.有些問題在初等數學中沒有得到充分的解決，但是應用高等數學知識就很容易解答.如函數的遞增性問題.

二、高等數學知識解決初等數學題的應用

1.用高等數學知識解決初等數學中不等式的問題

如可以利用柯西不等式或者用導數的性質證明不等式等.運用高等數學知識中的導數方法證明不等式，把需要證明的一元不等式通過構造成函數的方式轉化 成了關于x的函數，然后再通過求F(x)的最值的方法達到證明不等式的目的.進而打破了利用初等數學解不等式的局限性，也最終能夠使不等式這類問題得到充分的解決.

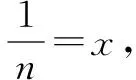
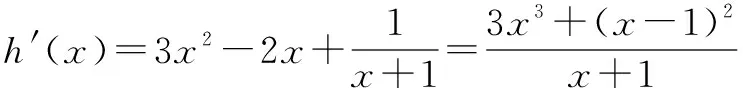
通過解題可知，當F(x)在[a,b]上單調遞增，則aF(a)．如果f(a)=φ(a)，要證明當x>a時，f(x)>φ(x)，那么，只要令F(x)=f(x)-φ(x)，就可以利用F(x)的單調增性來推導．也就是說，在F(x)可導的前提下，只要證明F′(x)>0即可．

2.高等數學中離散數學在初等數學問題中的應用

離散數學的內容包括數理邏輯、數論、圖論、集合論以及代數結構等知識.其中利用數理邏輯的方法解決初等數學問題，具有較強的概括性和推理便捷性，便于分析.

如對于若P則Q類的證明，可以順著P、Q的成立條件來進行分析，當P滿足時Q則滿足，意識P為Q的先導條件.可以假設P已經成立時，推導出Q是否成立，命題即可得到證明.具體證明實例如下.

3.常微分方程的建模技術應用

方程在實際問題的解決中占有非常重要的地位，它是解決問題的一種重要的方法.笛卡兒曾經設想過把任何問題轉化為數學問題然后再把任何數學問題轉化為代數問題，再指導代數問題歸結為解方程的萬能方法.雖然笛卡兒的設想沒有成功，但是它仍然是個偉大的思想.常微分方程建模技術的形成，讓方程的思想發揮越來越重要的作用.如有一個空水池，如果單獨灌水需24個小時灌滿，單獨排水需48小時.如果同時灌水和排水，用多少小時可將空水池灌滿？可以設水池的容積為V，水池灌滿所需的時間為t建立方程，結果需要48小時灌滿水.但是在實際中，可以用灌水為衡量，排水是隨水池水位下降流量而不斷減少的.而簡單通過建立微分方程是無法灌滿水的，通過實驗或者觀察而求解的做法是行不通的.通過建立和處理數學模型，把數學理論知識運用于實際的問題中，問題就迎刃而解了.

用高等數學中的理論和方法對初等數學的相關問題進行分析，可以很好地拓寬學生的解題思路；把高等數學中的一些內容融合到初等數學中，還可促進學生更好地學習初等數學知識，使學生的思維更加靈活.