一種模糊PID控制器的設計與仿真
黃良沛, 鄒東升, 陳磊, 王岳峰
(湖南科技大學a.機械設備健康維護湖南省重點實驗室;b.機電工程學院,湖南湘潭411201)
0 引言
PID控制技術是工業過程控制中最廣泛使用的控制技術[1-15],PID控制技術建立在被控對象具有精確數學模型(傳遞函數和狀態方程)的基礎上[16],采用PID控制對被控對象進行控制時,通過調節PID控制器的3個控制參數Kp、Ki、Kd來獲得期望的控制效果。被控對象的數學模型精確,PID控制的控制效果較好。對于難以建立精確數學模型的復雜系統,PID控制的控制效果不理想。模糊控制在求解復雜系統時不依賴精確的數學模型,能實現參數的自適應調整,結合PID控制與模糊控制的模糊PID控制技術,具有模糊控制的參數自適應調整與PID控制技術控制精度高的優點,將模糊PID控制技術用于難以建立精確數學模型的復雜系統能獲得較好的控制效果,模糊PID控制器不依賴于精確的數學模型[17]對被控對象求解,而根據控制規則對PID控制參數實行自調整來獲得較好的控制效果,適用于復雜系統等建模不準確的系統。本文介紹了模糊PID控制器的工作原理及參數自整定調整的原理;確定了模糊PID控制器的模糊論域與隸屬度函數;制訂了模糊PID控制器的控制規則;設計了一種模糊PID控制器并以二階系統作為測試系統,考慮加入干擾的影響,以模糊PID控制器與常規PID控制器同時對系統進行控制,并對兩者的控制性能進行對比分析性能,分析結果更具有意義。
1 模糊PID控制器的設計
1.1 模糊PID控制器的工作原理
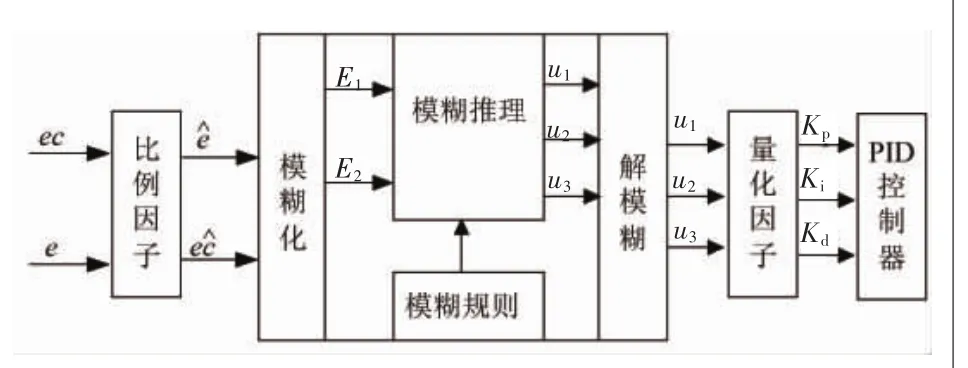
圖1 模糊PID控制器結構示意圖
模糊PID控制器的輸入為誤差e和誤差變化率ec,誤差為反饋值與控制設定值通過對比所得,輸出為PID的三個調節參數Kp、Ki、Kd。控制器工作時,首先通過比例因子Ke和Kec將誤差和誤差變化率轉化到標準值e^、ec^∈[-1,1],再經過模糊化處理將標準值e^、ec^生成模糊變量E1、E2,然后基于Mamdani算法和模糊推理規則求解出U1、U2、U3。最后經過解模糊方法(如最大隸屬度法,加權平均分等)得到標準化u^1、u^2、u^3再乘以相對應的量化因子k1、k2、k3即得到PID調節值Kp、Ki、Kd。將調節值傳入控制器即可對被控對象實行控制。模糊PID控制器結構如圖1所示。
1.2 模糊PID控制器的論域與隸屬度函數
設定模糊推理的輸入e和ec的論域均為 {-3,-2,-1,0,1,2,3},對應的語言值為{負大(NB),負中(NM),負小(NS),零(ZO),正小(PS),正中(PM),正大(PB)},采用的隸屬度函數均為三角形(trimf);設定模糊推理的輸出Kp、Ki、Kd的論域均為{1,2,3,4},對應語言值{零(ZO),正小(PS),正中(PM),正大(PB)},采用的隸屬度函數為三角形(trimf),Z型(zmf)和S型(smf)三種。模糊推理使用隸屬度函數的大小表征誤差的大小,影響模糊PID控制器輸出的PID調節值的大小。
1.3 模糊PID控制器的控制規則
模糊控制規則是模糊PID控制器中最重要的一部分,決定著模糊PID控制器的控制精度與控制性能。在系統處于不同的e和ec值時,為了獲得好的控制結果,需要設定以下模糊控制規則:當誤差e的絕對值與誤差變化率ec的絕對值較大時(誤差語言值為正大或正中,對應論域分別為±3,±2),為了降低調整時間,初始Kp調節值要取較大值(Kp語言值為正大,對應論域為4);為了保證系統在可控范圍內,Kd值應該較小(Kp語言值為0,對應論域為1);為了防止控制過程中系統出現較大的超調量,應限制積分環節,Ki取值應該極小(Ki語言值為正小,對應論域為2。當誤差e的絕對值與誤差變化率ec的絕對值適中時(誤差語言值為正中或正小,對應論域分別為±2、±1),為了降低超調,Kp值應稍微降低(Kp語言值為正大,對應論域為4);系統響應速度取決于Kd的取值,此時Kd值應適中(Kd語言值為正小或正中,對應論域分別為2、3)。同時為了增強控制效果,Ki值不宜太大(Ki語言值為正小或零,對應論域分別為2、1)。當誤差e的絕對值與誤差變化率ec的絕對值較小時(誤差語言值為正小或零,對應論域分別為±1、0),為了獲得好的穩態性能,取較大的Kp(Kp語言值為正大,對應論域為4),Ki(Ki語言值為正大,對應論域為4);此時系統可能出現振蕩現象,為防止出現這種現象,當e的絕對值與誤差變化率ec的絕對值趨向于減小,Kd取較大值(Kp語言值為正大,對應論域為4),當e的絕對值與誤差變化率ec的絕對值趨向于增大,Kd取較小值(Kp語言值為零,對應論域為1)。根據以上分析,可以總結出Kp、Ki、Kd的自調整規則,如表1所示。
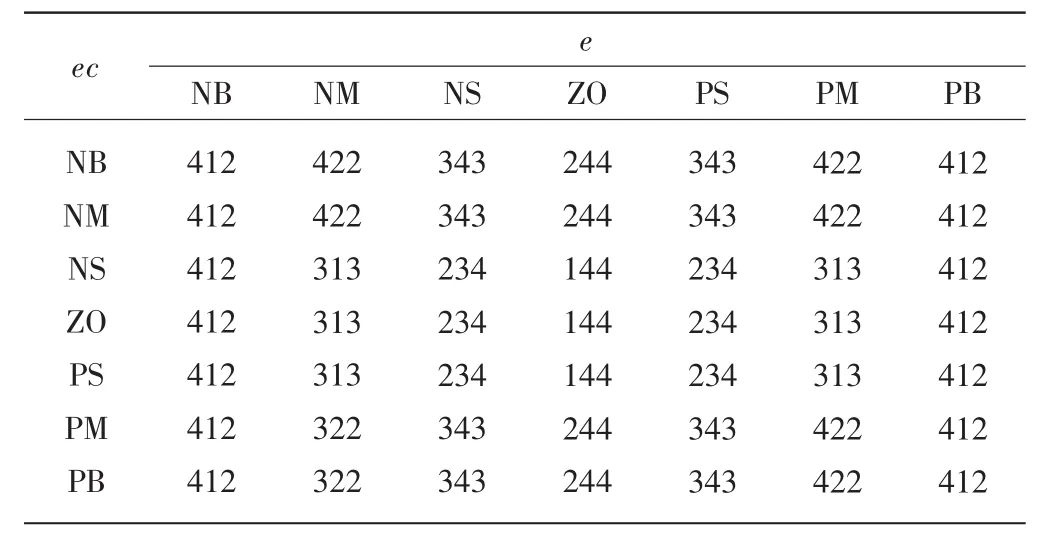
表1 模糊PID控制規則中Kp、Ki、Kd值查詢表
根據模糊PID控制器的隸屬度函數、論域及控制規則查詢表,可在MATLAB軟件中的fuzzy工具箱生成模糊PID控制器,生成的模糊PID控制器為兩輸入,三輸出系統,包含49條模糊規則。輸入變量e、ec的隸屬度曲線如圖2所示,輸出變量Kp、Ki、Kd的隸屬度曲線如圖3所示。
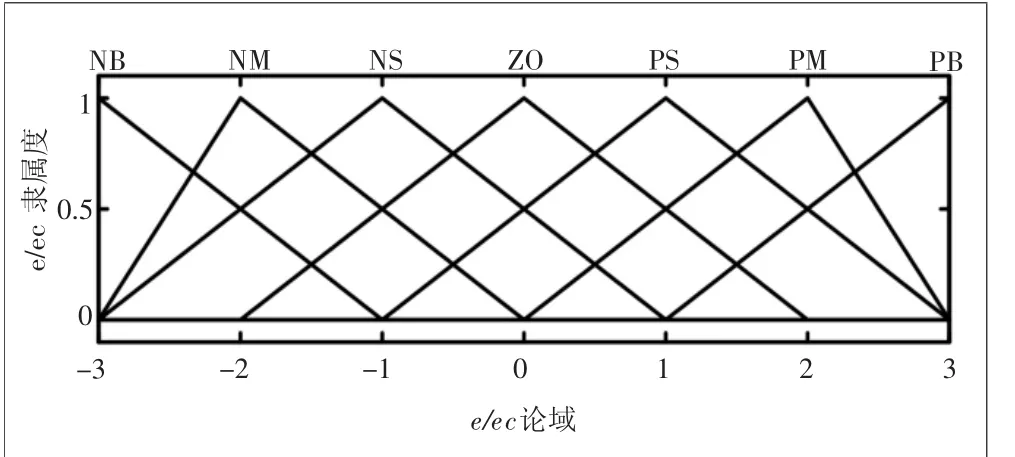
圖2 輸入變量隸屬度曲線

圖3 輸出變量隸屬度曲線
1.4 模糊PID控制器參數自整定原理
由表1可知:模糊PID控制器的調整參數由三個參數決定:e,ec的絕對值對應的論域和PID控制參數的論域。設定某時刻e,ec的絕對值|e|、|ec|已知。根據表1,可寫出PID調節器中Kp對應的每條調整規則,如第一條可寫為:R1:if|e|=NB and |ec|=NB then Kp=PB。
該條規則隸屬度計算公式為
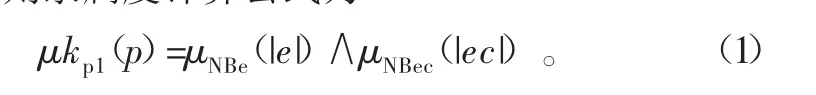
式中:μNBe(|e|)表示誤差e對應語言值為NB時的隸屬度函數,μNBc(|ec|)表示誤差變化率ec對應語言值為NB時的隸屬度函數;同理可求出Kp的其他所有規則的隸屬度μkpi(p)(i=1,2,3···,n),其中,n為Kp的總規則條數,pi為第i條規則中Kp所取論域的中心值。
Kp調整值的計算公式為
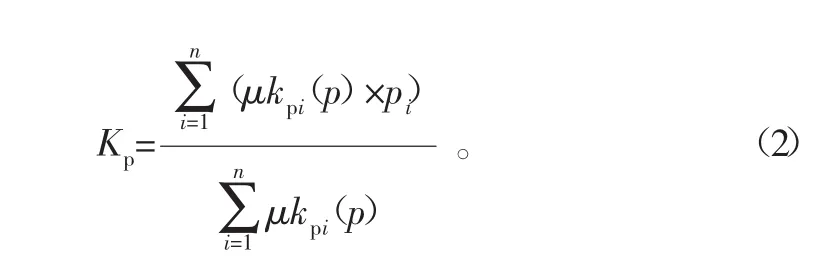
同理可以得出Ki,Kd的計算公式,其中μkIi(I)(i=1,2,3···,n) 為Ki所有規則的隸屬度,l為Ki的總規則條數,Ii為第i條規則中Ki所取論域的中心值;μkdi(D)(i=1,2,3···,n)為Kd所有規則的隸屬度,其中n為Kd的總規則條數,Di為第i條規則中Kd所取論域的中心值。計算公式如下所示:

由式(1)~式(4)中可知,Kp、Ki、Kd調整值與誤差、誤差變化率之間存在著函數關系,滿足了系統在不同e、ec狀態下對PID控制參數的調節需要。在MATLAB軟件中的fuzzy工具箱可查看模糊PID控制器在不同誤差和誤差變化率下的PID控制參數調整值,下面列舉一些在不同誤差和誤差變化率下的PID控制參數調整值。誤差隸屬度為0.5,誤差變化率隸屬度為0時,Kp調整值為1.1,Ki調整值為1.92,Kd調整值為1.58。誤差隸屬度為1.5,誤差變化率隸屬度為0時,Kp調整值為1.5,Ki調整值為1.48,Kd調整值為1.53。誤差隸屬度為0,誤差變化率隸屬度為0.5時,Kp調整值為1.12,Ki調整值為2.2,Kd調整值為1.7。誤差隸屬度為0,誤差變化率隸屬度為1.5時,Kp調整值為1.25,Ki調整值為2.2,Kd調整值為1.72。由以上數據可知控制參數是實時調整的,滿足了系統在不同e,ec狀態下對PID控制參數的調節需要。
2 模糊PID控制器建模與仿真分析
2.1 模糊PID控制器建模
在MATLAB/simulink仿真軟件下建立系統仿真模型,模型主要由模糊PID控制器,干擾信號,被控系統(被控對象),控制設定值等組成,如圖4所示。
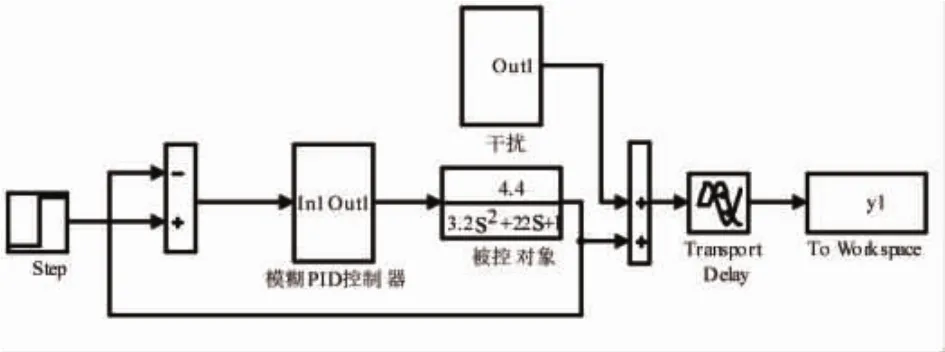
圖4 仿真模型
2.2 模糊PID控制器仿真分析
選擇二階系統G(S)=4.4/(3.2S2+22S+1)作為被控系統進行仿真,測試信號為單位階躍信號,分別在無干擾和加入隨機干擾條件下進行仿真,仿真結果分別如圖5、圖6所示。
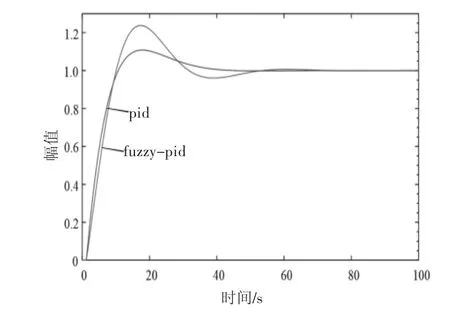
圖5 無干擾仿真結果
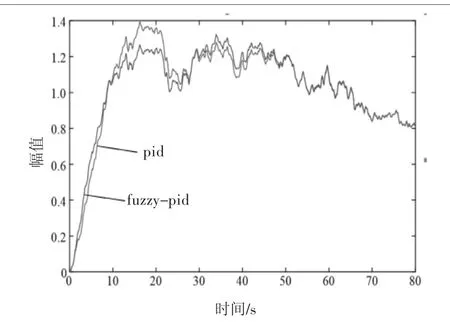
圖6 有干擾仿真結果
測試信號為單位階躍信號,即控制設定值的大小為1。將圖5進行處理后可以得到以下結論:在無干擾條件下,在模糊PID控制器控制下,系統的調整幅值峰值為1.08,經計算可知其超調量為8%;調整時間為41 s。常規PID控制下,系統的調整幅值峰值為1.25,經計算可知其超調量為24%,調整時間為72 s。在兩種控制器控制下,系統的響應時間相差不大。在有干擾條件下,模糊PID控制器的控制效果也要優于常規PID控制器的控制效果。

