基于改進型支持向量機的偵察無人機作戰效能評估*

陳 俠，胡乃寬

（沈陽航空航天大學自動化學院，沈陽 110136）

0 引言

當前軍用無人機的主要使命仍然是執行戰場偵察任務。由于作戰理念的不斷更新和現代化武器的不斷列裝，作戰環境越來越復雜多變，因此，有必要預先對偵察無人機的作戰效能進行評估。為了客觀準確地對偵察無人機作戰進行效能進行評估，本文提出了基于粒子群算法優化支持向量機的偵察無人機作戰效能評估方法。支持向量機是一種新的機器學習方法，其是根據統計學習理論發展而來的，具有較快的收斂速度和較強的泛化能力，并且能夠以任意的精度逼近非線性函數。除此之外，該方法還解決了貝葉斯網絡[1]，灰色關聯分析法[2]，層次分析法[3]，ADC 法[4]，模糊推理法[5]等傳統方法需要專家評估出各個作戰效能影響因素的權重的缺點，降低了作戰效能評估的主觀性。但是支持向量機應用在無人機作戰效能評估時，需要選擇合適的懲罰參數c和核函數參數δ，才能獲得精確的效能評估結果[6]。而以往支持向量機的懲罰參數c和核函數參數δ是根據經驗來選取的，因此，具有一定的局限性[7]。為了解決人為設定懲罰參數c和核函數參數δ的盲目性，本文采用粒子群算法尋找最優懲罰參數c和核函數參數δ。粒子群算法是一種基于群智能的優化算法，該算法可以通過粒子的不斷迭代尋優，搜索到最優懲罰參數c和核函數參數δ，使得支持向量機表現出更加優異的性能[8]。因此，本文采用基于粒子群算法優化支持向量機的方法對偵察無人機作戰效能進行評估，并通過仿真實驗證明了該方法具有較高的評估精度。

1 支持向量機回歸模型

支持向量機回歸算法的基本思想是將輸入空間的樣本通過非線性映射傳遞到高維特征空間，并且在這個高維特征空間下進行線性函數擬合，進而實現偵察無人機的作戰效能評估功能[9]。在解決不同的實際工程問題時，應該結合問題的特點選取恰當的核函數類型和核函數參數δ。其中在作戰效能評估領域，徑向基核函數是一種常用的核函數，該核函數的表達式如下：

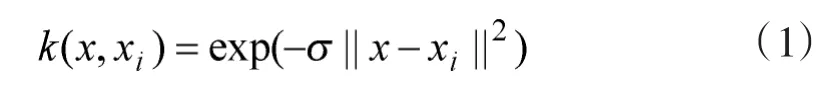
其中，δ是核參數。為了提高支持向量機的評估精度，需要選擇合適的懲罰參數c和核參數δ。其中懲罰參數c實現了函數擬合精度和算法復雜度的折衷，而核參數δ的選取會直接影響到支持向量機的泛化性能。

2 粒子群算法

粒子群算法[10]是一種基于群智能的隨機優化算法，其通過制定種群中的各個粒子的運動規則，使得整個粒子群表現出復雜的特性，用來求解復雜的問題。其中各個粒子的速度和位置更新公式分別如式（2）和式（3）所示[11]。

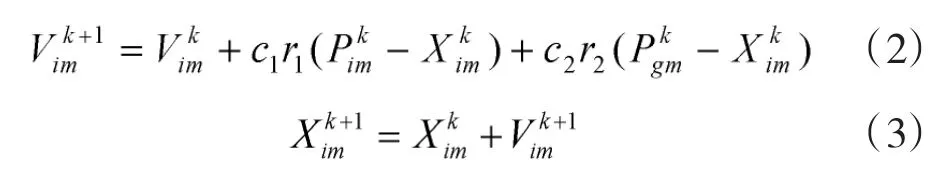
式中，Vim為粒子的速度；Xim為粒子的位置；c1和c2為加速度因子；r1和r2是介于[0，1]之間的隨機數；；為當前迭代次數。

3 PSO-SVM預測模型的建立

本文通過建立基于粒子群算法優化支持向量機的模型對偵察無人機進行作戰效能評估，而支持向量機性能的優劣主要取決于核函數參數c和懲罰參數δ[12-13]。當偵察無人機作戰效能評估模型的結構及參數確定后，其評估的具體步驟如下：

步驟1：初始化支持向量機參數。s選擇為4，即v-SVR；核函數類型t選擇2，即徑向基函數。懲罰參數c和核函數參數δ用粒子群算法進行搜索，其初始值和其他參數一樣選取默認值。

步驟2：粒子群算法參數的設定。根據所設置的粒子的維數，設定加速度因子；迭代次數為1 000次；種群規模為50，其他參數采用系統默認[14]。

步驟3：將初始懲罰參數c和核函數參數δ賦給支持向量機，然后根據適應度函數計算每個粒子的適應度值。根據需要，本文選用支持向量機輸出的相對誤差和作為粒子群的適應度值。則適應度函數如式（4）所示。

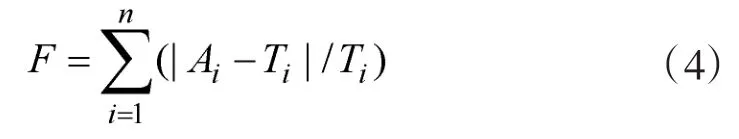
步驟4：判斷適應度值是否達到要求，如果達到要求，則將此時的懲罰參數c和核函數參數δ設置為最優參數，賦給支持向量機，進行偵察無人機的作戰效能評估。如果沒有搜索到最佳的懲罰參數c和核函數參數δ，則繼續迭代尋優。

步驟5：根據適應度值更新粒子群的個體極值和群體極值。

步驟6：根據式（2）和式（3）分別更新種群各個粒子的位置和速度，獲取相應的懲罰參數c和核函數參數δ，轉到步驟3繼續計算。

為了更加直觀地說明本文提出的粒子群優化支持向量機的步驟，本文制作了其流程圖如下頁圖1所示。

4 建立評估指標體系

為了提高對偵察無人機作戰效能的評估準確度，本文分析了影響其作戰效能的各種因素，歸納總結了影響其作戰效能評估的主要因素。本文建立的評估指標體系如下：航程，實用升限，情報獲取能力，情報處理能力，操作水平系數，環境影響系數[15]。

1）航程：航程指無人機依靠自身所攜帶的燃料而能夠飛行的最大距離。飛行距離的長短直接關系到偵察區域的大小。

圖1 粒子群優化支持向量機的流程圖

2）實用升限：實用升限是偵察機的工作高度。

3）情報獲取能力：信息獲取水平主要反映偵察設備的性能，可分為極強、強、弱、極弱4種。

4）情報處理能力：信息處理水平主要反映了機載設備的情報加工能力和加工后情報的傳輸性能。

5）操作水平系數：操作水平系數與偵察無人機作戰效能評估密切相關，受人員素質、人機界面和自動化程度的影響。

6）環境影響系數：反映了環境對偵察無人機作戰的影響程度，通常包括自然環境因素和人為環境因素。它可以分為4種：極弱、弱、強、極強。

5 實際算例與分析

設航程、實用升限、情報獲取能力、情報處理能力、操作水平系數、環境影響系數是影響偵察無人機作戰效能評估的6個因素，對應著粒子群算法優化支持向量機（PSO-SVM）評估模型的6個輸入節點，而PSO-SVM評估模型的輸出對應著偵察無人機的作戰效能評估值。

本文選取1～1 000組樣本為PSO-SVM評估模型的訓練樣本，1 001～1 007組樣本為測試樣本。為了證明PSO-SVM的評估模型有較高的評估精度。本文構建了用于和PSO-SVM評估模型作對比的粒子群算法優化BP（PSO-BP）神經網絡的評估模型和BP神經網絡。為了客觀公正地證明本文提出的評估模型具有較高的評估精度，本文使用同樣的訓練樣本，分別對PSO-SVM評估模型、PSO-BP神經網絡和BP神經網絡進行訓練，待3個評估模型訓練結束后，分別向PSO-SVM評估模型、PSO-BP神經網絡和BP神經網絡輸入測試樣本，得到了PSO-SVM評估模型、PSO-BP神經網絡和BP神經網絡的輸出評估值與期望輸出的對比曲線圖如圖2所示。從圖2中可以直觀看出，相對于PSO-BP神經網絡和BP神經網絡輸出評估值，PSO-SVM評估模型的輸出值與期望輸出的擬合程度更高，更能得到符合實際的評估結果。

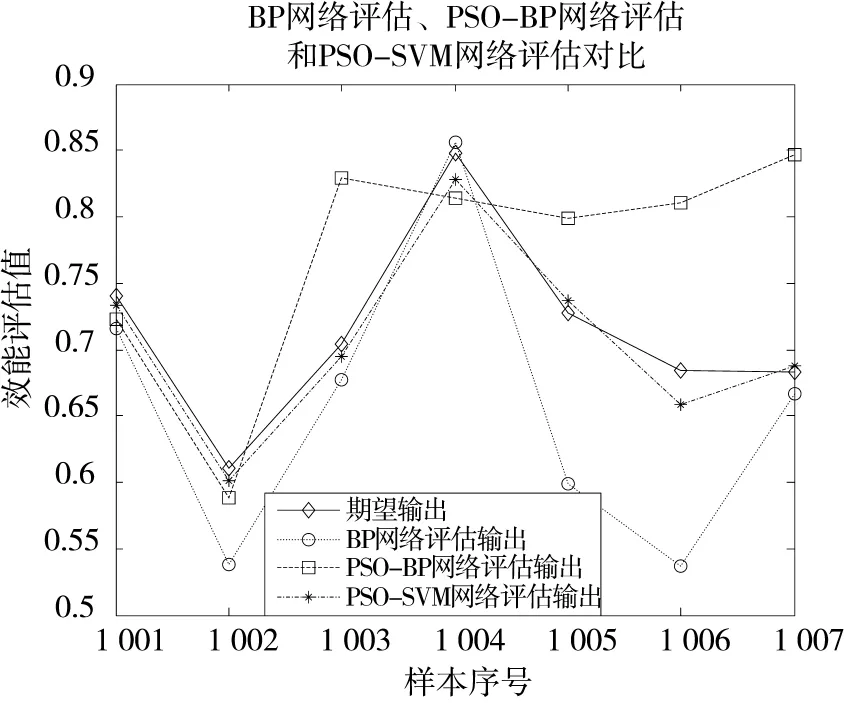
圖2 預測輸出結果對比

本文對PSO-SVM評估模型、PSO-BP神經網絡和BP神經網絡的評估值分別與期望輸出比較，得到了輸出誤差曲線如圖3所示，相對誤差曲線如圖4所示。從圖3和圖4中可以直觀地看出，PSO-SVM評估模型的輸出誤差和相對誤差相對穩定且趨向于0，而PSO-BP神經網絡和BP神經網絡的輸出誤差及相對誤差都相對較大，反映PSO-SVM評估模型對偵察無人機作戰效能評估的可信程度更高。

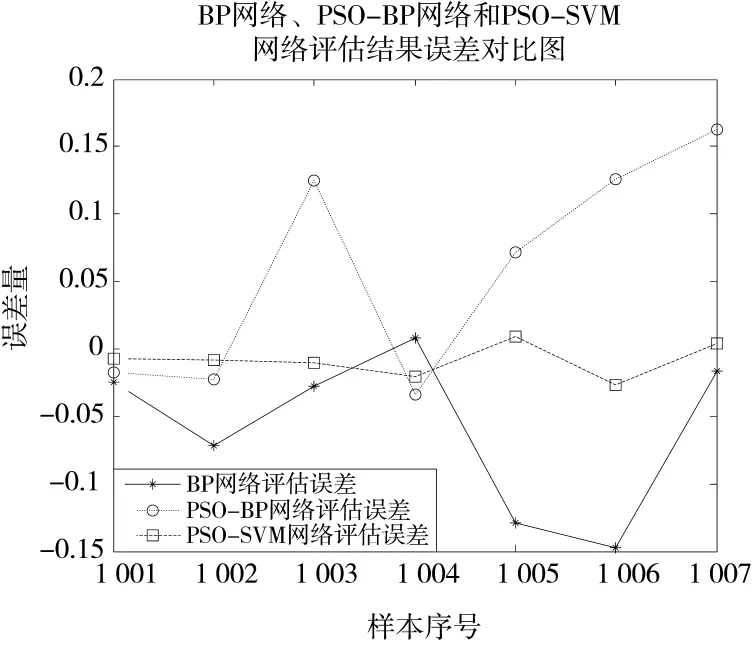
圖3 預測誤差曲線

6 結論

本文構建了PSO-SVM評估模型對偵察無人機作戰效能進行評估。PSO-SVM評估模型是利用粒子群算法選擇支持向量機的最佳懲罰參數c和核函數參數δ，然后用樣本數據對PSO-SVM評估模型進行訓練和評估。通過實例證明相對于PSO-BP神經網絡和BP神經網絡評估模型，PSO-SVM評估模型可以得到精度更高的輸出值，取得了很好的評估效果。這種基于群智能算法優化的支持向量機具有強大的信息處理能力，可以用來處理復雜的非線性問題，得到精度較高的輸出結果，具有較高的實用價值。

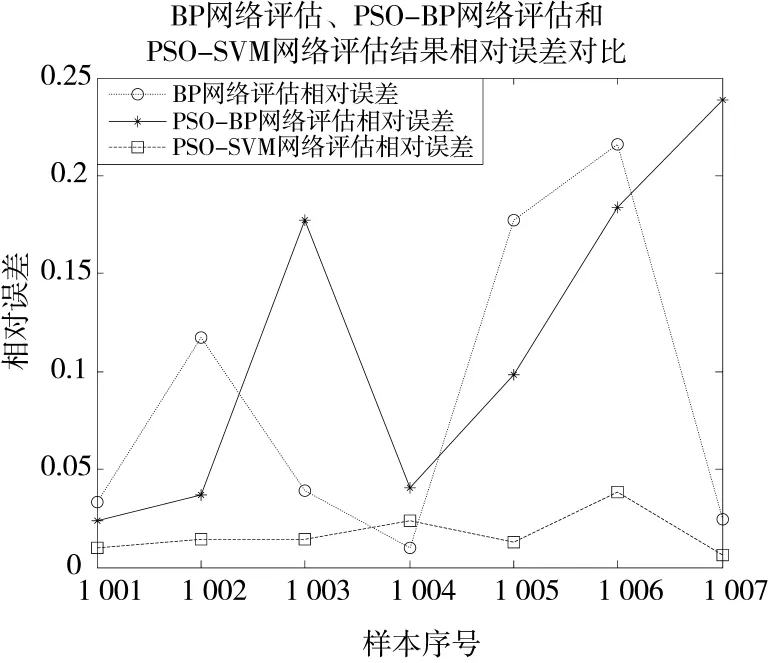
圖4 相對誤差曲線