支腿-輪胎載荷分配比對混合支撐發射過程的影響*

王玲麗，馬大為，張震東，朱忠領，王澤林

（南京理工大學機械工程學院，南京 210094）

0 引言

導彈無依托隨機發射是一種新型作戰模式，在作戰過程中，導彈發射將不需要依托預設陣地，隨機選取發射場地，即時進行戰斗[1]，這種導彈無依托發射方式相較于傳統發射方式在很大程度上節省了發射準備時間，提高了作戰效率。

現有的導彈發射裝置的支撐方式包括剛性支撐，混合支撐，柔性支撐。剛性支撐是指導彈起豎與發射過程中載荷完全通過千斤頂傳遞到地面；混合支撐是支腿與輪胎同時承受載荷；而彈性支撐指載荷僅通過輪胎傳遞到地面。鄭夏[2]研究了發射箱箱口回彈的變化規律，提出將箱口回彈情況納入出箱安全性分析因素的方法。閆攀運[3]建立了車載系統快速仿真模型，研究了發射管底座-支腿載荷分配比和附加因子對發射穩定性的影響。高星斗[4]研究兩種不同發射角下車載導彈傾斜發射對導彈發射箱體振動的影響。陳大雄[5]驗證了車載導彈發射時柔性支撐的可行性。

目前，尚未有人針對混合支撐支腿、輪胎載荷分配比對導彈發射穩定性有何影響做出研究。本文基于顯式動力學方法，運用有限元分析軟件ABAQUS對導彈系統發射過程進行建模仿真運算，針對某型導彈在混合支撐這種支撐方式下，研究不同支腿、輪胎載荷分配比對導彈發射過程中穩定性的影響。

1 顯式非線性動力學

1.1 動力學問題基本方程

非線性動力學求解的基本方程形式如下[6]：

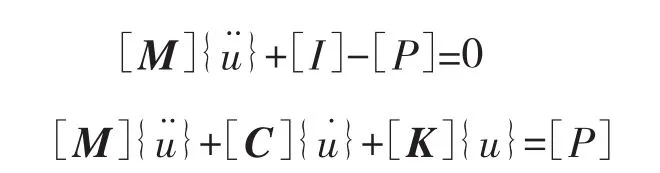
其中：[M]為質量矩陣；[C]為阻尼矩陣；[K]為剛度矩陣；為粘性效應項，考慮阻尼、粘塑、粘彈等效應；[P]為外部激勵作用；為節點加速度向量；為節點速度向量；為節點位移向量。

1.2 顯式時間積分

1）節點計算

①動力學平衡方程

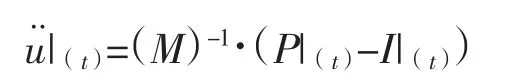
②對時間顯式積分

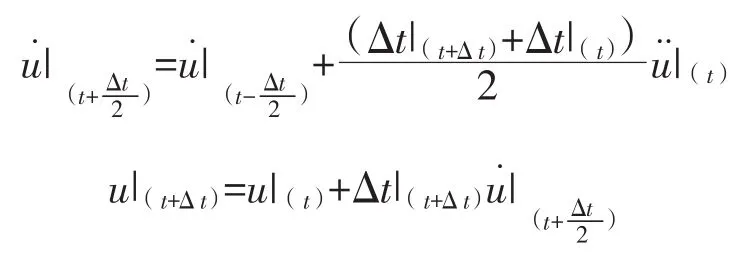
2）單元計算

②根據本構關系計算應力σ：

3）設置時間t為 t+△t，返回到步驟1）

顯式方法最顯著的特點是沒有整體切線剛度矩陣，而且由于是顯式地前推模型的狀態，所以不需要迭代和收斂準則。

1.3 顯式方法的條件穩定性

穩定性限制以系統中最高頻率（ωmax）來定義。無阻尼的穩定性限制由下式定義：

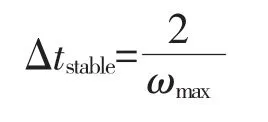
有阻尼的穩定性限制由下式定義：

式中，ξ為最高頻率模態的臨界阻尼。

2 導彈發射系統仿真模型

2.1 系統簡化

車載導彈武器系統主要包括發射車、起豎裝置、發射裝置、導彈等組成部分。導彈在發射過程中力學環境非常復雜，本文在計算時只考慮發射裝置對發射過程的影響。圖1為某雙聯裝導彈發射系統簡化示意圖。

圖1 車載導彈系統混合支撐簡化模型

如圖1所示，整個車載導彈系統簡化為車頭、車架、發射箱、導彈、支腿、輪胎、起豎油缸、適配器等部件；該模型中將彈體簡化為剛體，車頭簡化為質量點，耦合于車架上，其余部件均設置為可變形體，為了簡化建模，將系統中的起豎液壓油缸、支腿、輪胎、懸架等用彈簧阻尼代替，車橋、車輪軸等用梁單元簡化，由于混合支撐方式中，支腿的變形量遠小于輪胎的變形量，所以設定支腿處的連接單元屬性為剛性連接。

整個發射系統可以看作關于面對稱的結構[7-9]，規定與發射車前進方向為Y軸正向，Z軸的正方向沿著重力垂直向上，X軸根據右手定則確定。

2.2 輪胎、支腿載荷分配

混合支撐采用的支腿與輪胎共同支撐，整個導彈發射系統（不含地面）質量約為2.35×104kg，以支腿、輪胎各承受一半的載荷為例，即發射系統8個輪胎共承受1.175×105N，由于整個發射系統質心不是處于模型的幾何中心。經過測量，整個導彈系統的質心所在位置如圖2所示。其中，F1、F2、F3、F4分別表示沿Y軸方向從左往右四組車輪中每組車輪所承受的載荷。

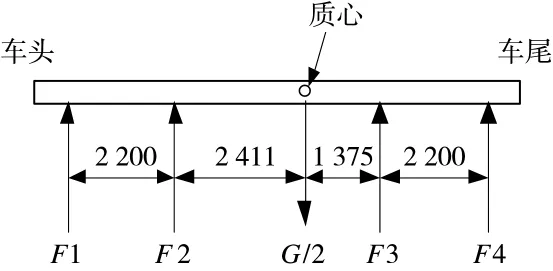
圖2 輪胎承受一半重量時輪胎受力圖

將其簡化為平面力，根據平面力系平衡方程

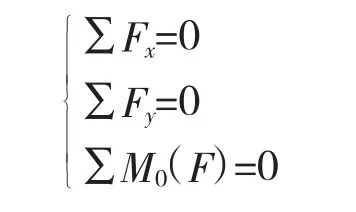
為了簡化計算，將導彈發射車前兩組輪胎所受載荷等效為大小相同的載荷，即F1=F2，同理，后兩組輪胎所受載荷F3=F4，由此計算出

2.3 載荷分配工況

設支腿所承受的總載荷為Q1，發射系統總重為Q2，定義支腿承載占總重的比例為R，其中，

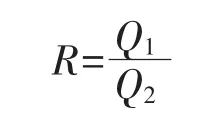
R值選取3個代表性的數值進行分別進行計算，選定R值為1/4，1/2，3/4分別進行計算，由于導彈發射系統動力學分析計算動態響應之前需要進行靜平衡分析得到系統的平衡位置，將計算出的初始受力狀態導入導彈發射系統的動態模型。

3 仿真結果與分析

計算結果顯示導彈完全出筒時間約為0.822 s。本文主要從發射車穩定性以及導彈出筒品質這兩方面考慮支腿、輪胎載荷分比配對導彈發射過程的影響。

3.1 支腿、輪胎載荷分配對發射車穩定性影響

以導彈前進方向的視角為正方向，發射系統分為左右兩側，選取左側輪胎動態響應進行分析。圖3、圖4分別為導彈左前輪與左后輪在導彈發射過程中輪胎載荷隨時間變化曲線。

由圖3、圖4可看出，R值越小，輪胎在法向上的位移越大，R值不同，但前后輪胎在法向上的位移量隨時間的變化規律基本一致。左后輪R值為1/4與R值為3/4時，其同一時刻位移量相差約為6.54 mm，而左前輪R值為1/4與R值為3/4時，其同一時刻位移量相差約為3.62 mm。同時，對比圖3、圖4可發現，由于后輪所承受的載荷比前輪大，發射車后輪位移量隨R值變化的影響比前輪大。

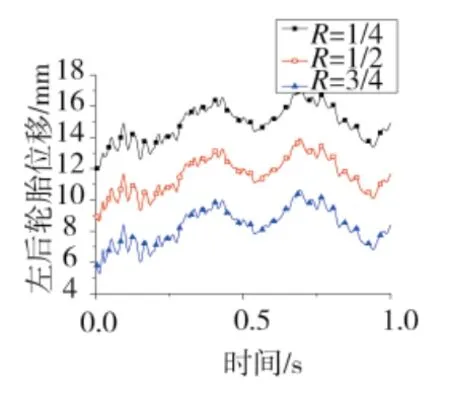
圖3 左后輪位移曲線

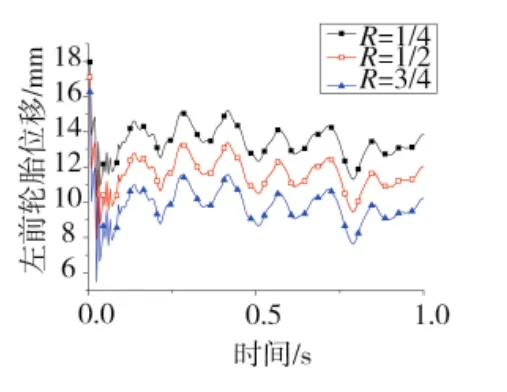
圖4 左前輪位移曲線

圖5為左前輪與左后輪在3種工況下輪胎所受載荷隨時間變化曲線，從圖中可以看出，R值分別為1/4，1/2，3/4時，左前輪與左后同一時刻所受法向輪載荷相差約為5.3 kN，3.6 kN，1.9 kN。輪胎所分配載荷越大，前后輪法向載荷差值越大，后輪相較于前輪負擔更重，這與載荷分配比的大小與輪胎在法向位移上的影響是一致的。

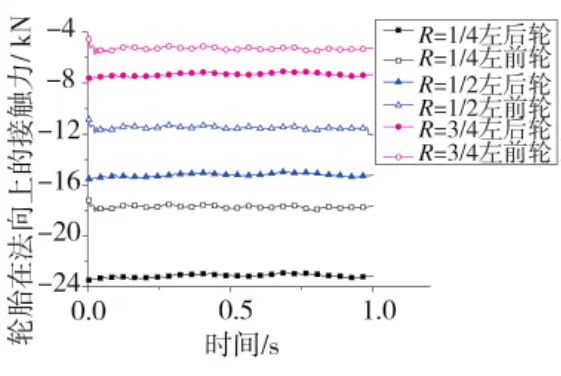
圖5 輪胎載荷隨時間變化曲線

圖6 駕駛室垂向位移曲線

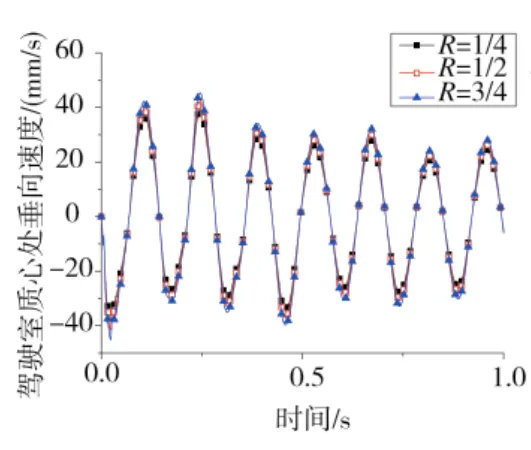
圖7 駕駛室垂向速度曲線

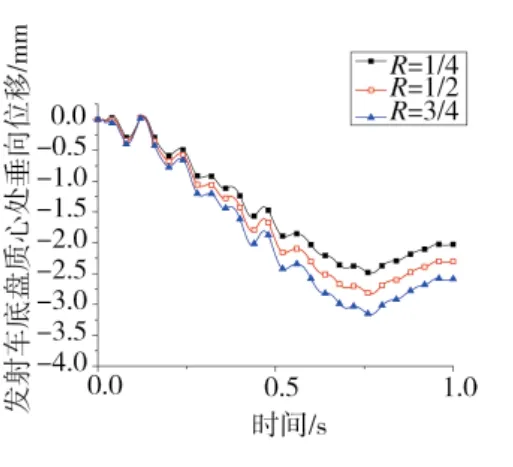
圖8 發射車底盤垂向位移曲線

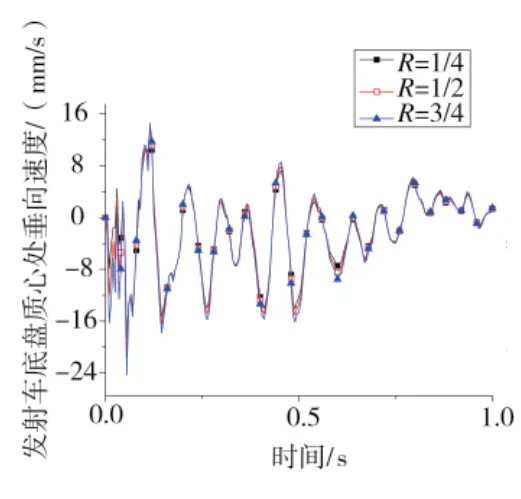
圖9 發射車底盤垂向速度曲線

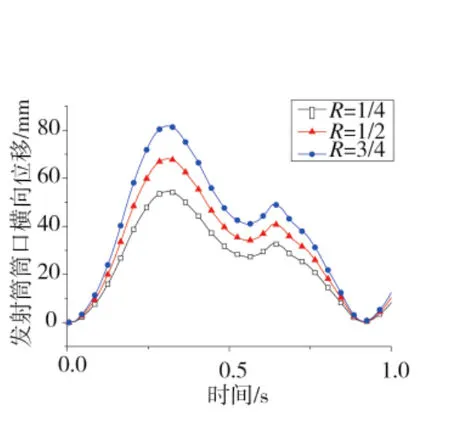
圖10 發射筒筒口橫向位移曲線

圖6、圖7為導彈系統中駕駛室的垂向位移曲線與垂向速度曲線，圖8、圖9為發射車底盤質心處的垂向位移曲線與垂向速度曲線。通過駕駛室以及發射車底盤處的位移與速度隨R值的變化的對比圖可發現，R值為3/4時，駕駛室與底盤質心在垂向上的波動最大。

3.2 支腿、輪胎載荷分配比對導彈出筒的影響

圖10、圖11分別為發射筒筒口橫向位移、縱向位移隨時間變化曲線，導彈發射初始時，筒口橫向位移與垂向位移均時間增大，0.3s處，垂向與縱向位移均達到最大，之后位移呈減小趨勢。表1為不同支腿、輪胎載荷分配比下發射筒橫向、垂向位移在0.3 s的位移量。由表1可知，R為1/2相較于R為1/4的橫向位移峰值增大了25.13%，垂向位移峰值增大了11.17%，R為3/4相較于R為1/4橫向位移峰值增大了50.13%，垂向位移峰值增大了33.47%。

表1 發射筒位移峰值

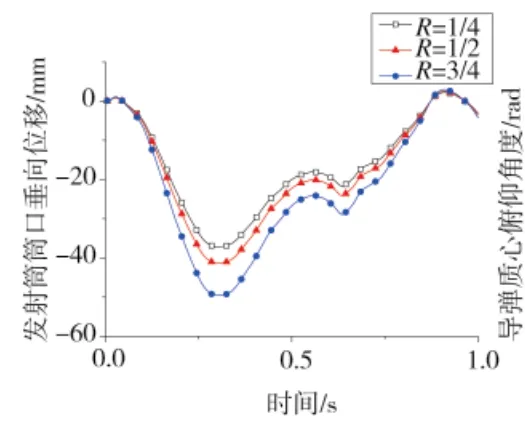
圖11 發射筒筒口垂向位移曲線

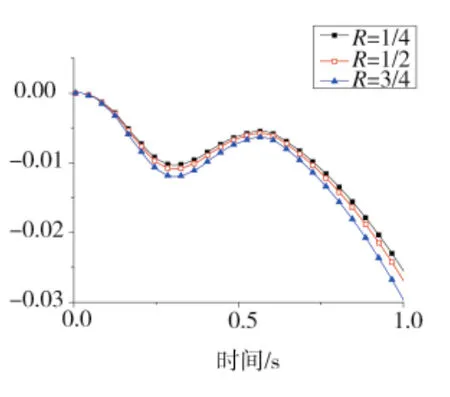
圖12 導彈質心俯仰角度曲線

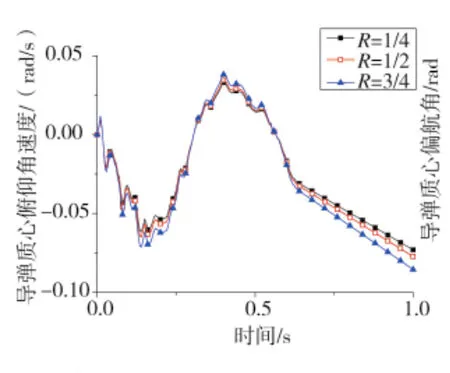
圖13 導彈質心俯仰角速度曲線

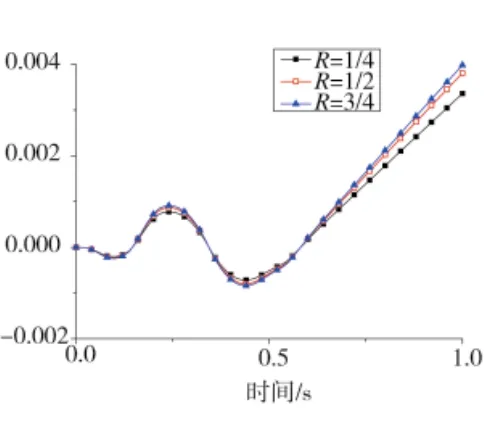
圖14 導彈質心偏航角度曲線

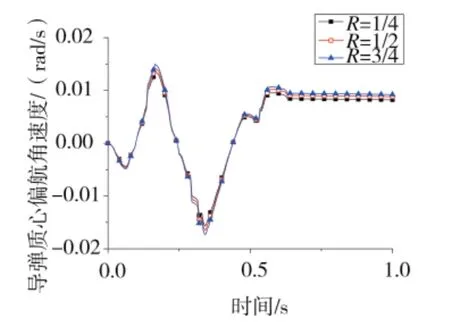
圖15 導彈質心偏航角速度曲線

圖12、圖13分別為導彈質心處的俯仰角度與俯仰角速度曲線，圖14、圖15分別為導彈質心處偏航角度與偏航角速度曲線。從這4幅圖可看出導彈質心處的俯仰角度與俯仰角速度以及偏航角度與偏航角速度在一定程度上均隨著R值的增大而增大。3種工況中，R為1/4時導彈俯仰角度與俯仰角速度以及偏航角度與偏航角速度均最小。

4 結論

本文通過在通用有限元軟件中建立的多體動力學模型，針對3種不同的支腿、輪胎載荷分配比進行分析，可以得出如下結論：

1）支腿、輪胎載荷分配比不同，在導彈發射過程中對輪胎在法向上的位移量有一定的影響，混合支撐時，輪胎所承受的載荷越大，輪胎在法向上的位移越大。

2）支腿、輪胎載荷分配比不同，在發射過程中對發射車的穩定性以及導彈出筒姿態也有一定的影響，綜合考慮駕駛室與發射車底盤質心處的縱向位移與速度，可以得出，對比這3種工況，R為1/4時，發射車在縱向上的跳動最小，在此種工況下發射車較為穩定。同時發射筒筒口的橫向位移與垂向位移較小，導彈的俯仰角速度與偏航角速度較小，導彈出筒姿態較好。

3）通過計算并分析3種工況下的導彈發射過程的動態響應，對比其導彈發射過程擾動的大小，為導彈發射裝置混合支撐時載荷分配的選擇提供了參考。