雷諾數對柱面屋蓋脈動風壓非高斯特性與風壓極值的影響★

邱 冶 王曉夢 朱召泉

(河海大學土木與交通學院，江蘇 南京 210098)

0 引言

大跨屋蓋結構因造型優美且受力合理，被廣泛地運用于體育場館、機場航站樓和會展中心等公共建筑中。由于屋蓋結構周圍分離流和旋渦脫落等特征湍流的影響，其表面脈動風壓具有明顯的非高斯特性，此時中心極限定理的前提條件不再滿足，如果采用高斯模型來描述，往往會產生較大偏差[1]。葉繼紅等[2]研究了五種典型大跨屋蓋表面局部風壓的高斯和非高斯特性，非高斯分區往往集中在屋蓋迎風前緣、尾流區及角部區域，并建議適當提高相應的峰值因子取值。Liu等[3]研究了大跨鞍形屋蓋表面的脈動風荷載特性，受到分離流和錐形渦的影響，屋蓋高角部位的風壓具有明顯的非高斯特性。已有研究表明[4]，大跨曲面屋蓋的風荷載特性具有明顯的雷諾數效應，但研究大多針對平均和脈動風荷載，鮮有研究關注非高斯特性和極值風壓的雷諾數效應。

本文基于矢跨比1/3柱面屋蓋的風洞測壓試驗，分析了不同雷諾數下屋面脈動風壓的非高斯特性，對高斯與非高斯進行分區，同時利用風壓極值估計的改進獨立風暴法，獲得屋蓋表面極值風壓分布，并探討了雷諾數的影響。

1 風洞試驗

本次試驗在哈爾濱工業大學封閉回流式風洞中進行。柱面屋蓋模型采用有機玻璃制成，矢跨比R/D=1/3，寬跨比B/D=1。采用兩組不同跨度的測壓模型，分別為0.2 m和0.6 m，簡稱為小模型和大模型。試驗風速U在5 m/s～24 m/s之間變化，選取模型跨度D為特征長度，依據雷諾數定義Re=6.9×104UD，得到試驗雷諾數變化范圍為6.90×104～8.28×105。測壓信號采樣頻率為625 Hz，單個樣本時長20 s，每組風速均采集5個樣本數據。

2 試驗結果分析

2.1 脈動風壓的非高斯特性

對于非高斯信號，可使用三階和四階統計矩進行表征，稱為偏度(skewness)和峰態(kurtosis)，分別描述風壓信號概率密度函數曲線的偏離度和凸起程度，表達式如下：

(1)

(2)

其中，Cpimean和Cpirms分別為風壓系數Cpi(t)的平均值和方差。

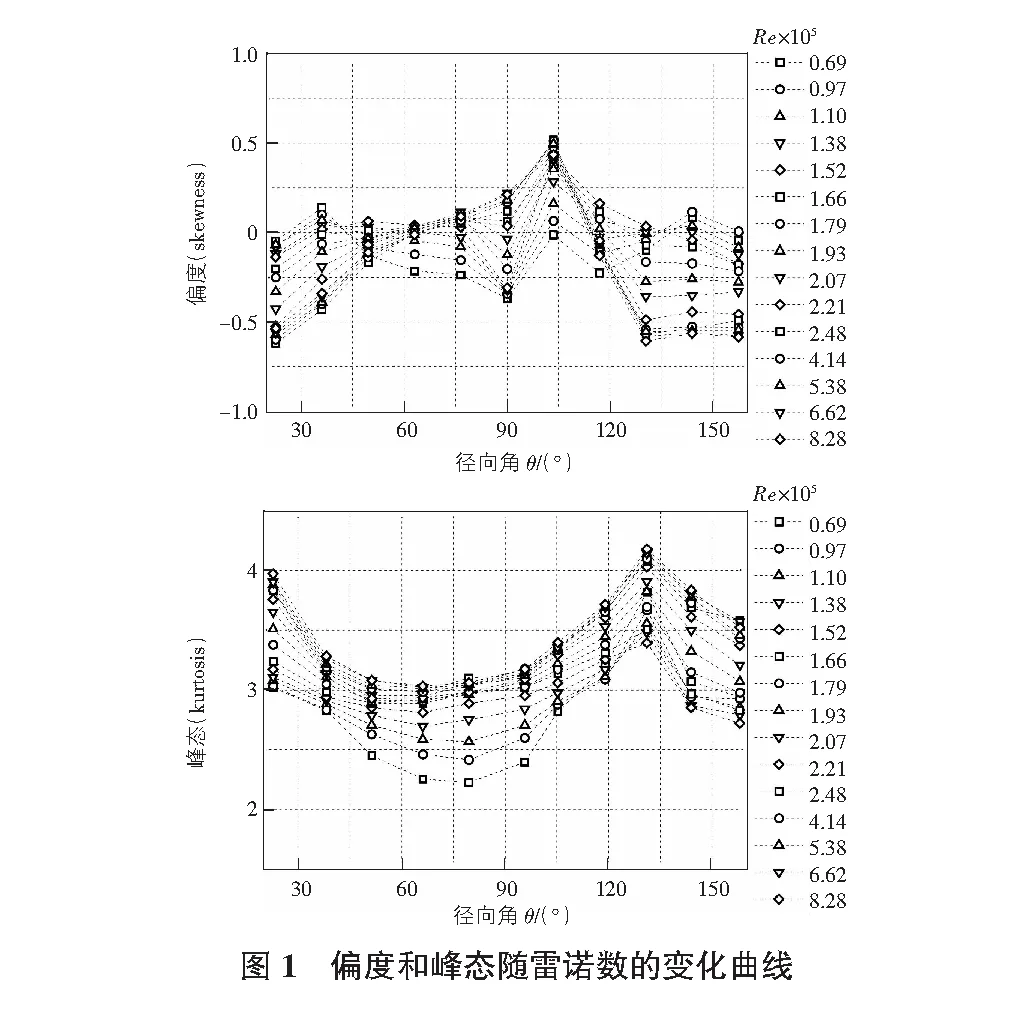
筆者在文獻[5]中對矢跨比1/3柱面屋蓋的風力系數—Re曲線進行了分析，已確定雷諾數轉捩區(Re=6.90×104～2.48×105)和超臨界區范圍(Re>2.48×105)。模型中心線條帶處的偏度和峰態分布隨Re的變化情況如圖1所示。在轉捩區間內，偏度和峰態明顯地受雷諾數變化的影響，且大部分測點具有較低的偏度(|Cpisk|<0.5)和峰態(Cpiku<3.5)，說明測點信號大多近似為高斯分布。但當Re>2.48×105時，偏度和峰態分布形式基本與Re無關，較大偏度(|Cpisk|>0.5)和高峰態(Cpiku>3.5)分別位于屋蓋迎風面(θ<38°)和尾流局部區域(θ>103°)。

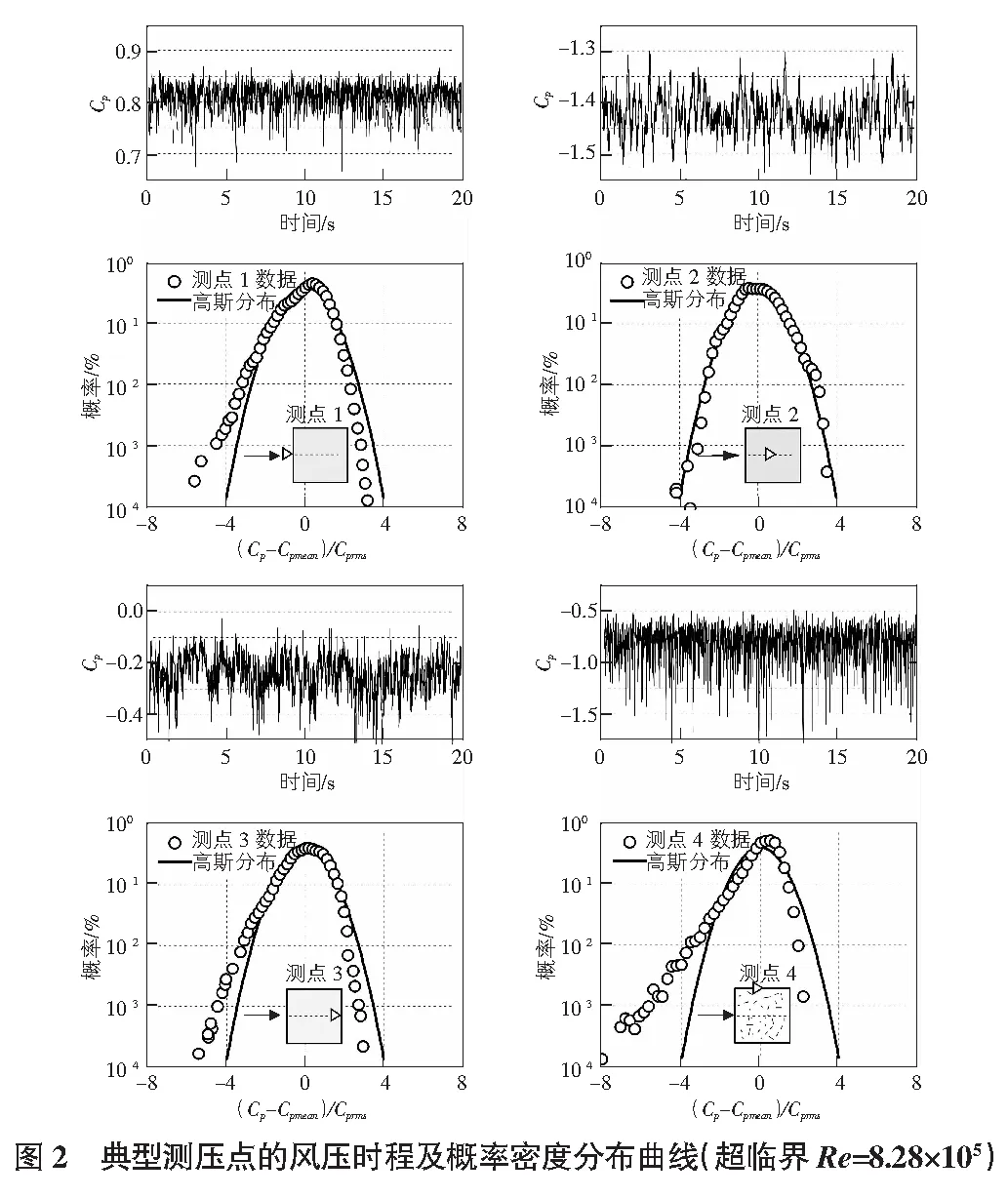
為探討脈動風壓非高斯特性產生的原因，圖2給出屋面典型測點的風壓時程曲線及概率密度分布曲線，限于篇幅，僅給出超臨界雷諾數情況(Re=8.28×105)。從圖2可知，在迎風前緣局部區域內(測點1)，受到柱狀渦的影響，風壓曲線具有明顯的不對稱性，帶有許多間歇性的脈沖信號。而處于迎風下游和頂部區域內的測點受到特征湍流的影響較小(測點2)，風壓曲線基本圍繞平均值波動，表現為高斯分布。在屋蓋尾流區域(測點3)以及兩側邊緣區域(測點4)的風壓信號則呈現顯著的非高斯特性。Qiu等[4]對柱面屋蓋繞流的研究可知，在尾流區域存在大尺度脫落旋渦結構，同時兩側邊緣區域的風壓脈沖主要與屋蓋側面的分離剪切流作用有關，故產生非高斯特性的原因可歸結為特征湍流的影響。

由于實際工程結構常處于超臨界或高超臨界范圍，因此本文僅根據超臨界Re試驗結果給出相應測點的高斯與非高斯區的所屬范圍。統計結果表明，在屋蓋迎風前緣、尾流區以及兩側邊緣區域的測點存在大偏度(|Cpisk|>0.5)和高峰態(Cpiku>3.5)，模型中部區域大部分測點都屬于小偏度和低峰態情況。鑒于此，本文將滿足|Cpisk|>0.5且Cpiku>3.5的測點劃分為非高斯區，其余屬于高斯區，如圖3所示。

2.2 雷諾數對風壓極值的影響

探討不同雷諾數下柱面屋蓋表面風壓極值的變化規律，對圍護結構的抗風設計具有一定指導作用。本文采用針對小容量樣本的極值概率分析方法(改進獨立風暴法)，來確定具有確定保證率的非高斯風壓極值，具體計算過程可參考文獻[6]。

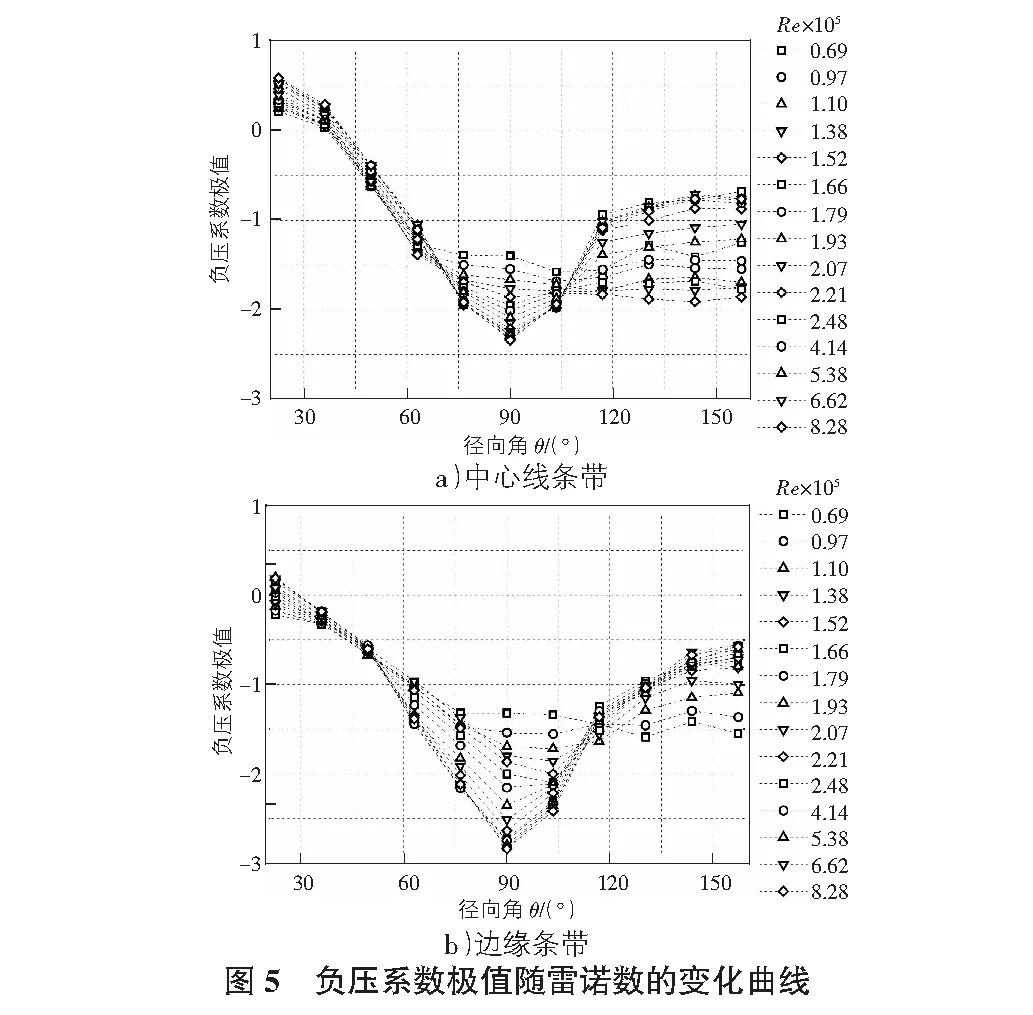
圖4給出了不同雷諾數下具有95%保證率的負壓系數極值分布。在轉捩區間(Re=6.90×104～2.48×105)內，負壓系數極值分布明顯地受雷諾數變化的影響，主要與分離流發生由層流向湍流狀態的過渡有關。隨著Re由6.90×104增大至2.48×105，屋蓋頂部區域的負壓極值逐漸增大，同時在兩側接近頂部區域，由于屋蓋側面分離剪切流對風壓脈動的影響增強，使得負壓極值隨著Re增加迅速增大。但當Re>2.48×105時，負壓系數極值分布基本不再依賴于雷諾數，最不利負壓極值出現在屋蓋邊緣局部區域。

3 結語

1)通過對風壓信號第三、四階統計矩進行歸納分析，在雷諾數轉捩范圍內(Re=6.90×104～2.48×105)，屋面脈動風壓主要呈現高斯特性，當Re>2.48×105時，屋蓋迎風前緣、尾流區及頂部邊緣附近表現出明顯的非高斯特性，并在此基礎上對高斯和非高斯區進行劃分；2)雷諾數對柱面屋蓋負壓系數極值分布的影響顯著。在雷諾數轉捩范圍內，屋蓋頂部及邊緣區域的負壓極值隨著雷諾數的增加而增大，但在超臨界范圍(Re>2.48×105)內，負壓極值分布基本與雷諾數無關，且幅值最大的負壓極值出現在屋蓋頂部邊緣區域。