含電力電子裝置電力系統戴維南參數頻域特性研究*

陳姍姍，查曉明，黃萌

(武漢大學 電氣工程學院，武漢 430072)

0 引 言

隨著半導體技術的發展，大量的電力電子裝置作為變換器或電子開關接入電力系統，電力電子裝置以其功率密度高、控制靈活等諸多優點，在電力系統的發、輸、配、用等各個環節得到廣泛的應用。電力電子裝置在電網中的滲透水平不斷提高，電力電子化成為電力系統的重要趨勢，電力系統正經歷著深刻的歷史性變革[1-2]。

電力電子裝置在提高電網輸電能力、改善電網運行狀態的同時，也給電網的穩定帶來了巨大的挑戰。傳統電網中，變壓器、發電機是主要的諧波源，諧波含量較小，一般可以忽略不計。而在電力電子化電網中，電力電子裝置是主要的諧波源，給電網造成較大的諧波污染[3]。電力電子裝置產生的諧波一是源于其具有拓撲時變的特性，功率開關器件的開通和關斷狀態的組合對應不同的拓撲結構，二是由于電力電子裝置中功率開關器件一般存在占空比控制，開關器件的占空比與狀態變量的瞬時值相關。所以，電力電子裝置成為了現代電網中又一種新的諧波源[4]。

戴維南等值是將電網等效為一個電壓源與阻抗串聯形式，是電網穩定性研究的重要方法之一[5-6]。在傳統電網中，由于諧波現象不明顯，僅考慮基波下的戴維南等值是可行的。但在電力電子化電網中，在基波條件下做電網的戴維南等效已不能完全反映實際電網的阻抗變化情況。因此，需要考慮戴維南參數的頻域特性，關鍵問題在于戴維南參數的獲得以及戴維南參數準確性的驗證。

目前，已有的戴維南參數跟蹤方法主要分為以下兩種[7]：(1)網絡解析法,按照戴維南定理求取開路電路和短路電流或通過導納矩陣求逆的方法直接求取戴維南阻抗[8]；(2)基于潮流結果的方法，根據計算過程中使用的時刻點可以分為單時間斷面法[9]和多時間斷面法[10-11]。這兩類方法考慮了穩態下、小擾動下及大擾動下的三類場景，但均是在基波條件下做電網的戴維南等效。戴維南參數的取值與負荷特性、故障擾動、發電機調節和系統控制等因素均相關[12-13]。系統接入若干電力電子裝置后，若將其看成是一種特殊的負荷，則系統的阻抗特性會發生變化。

基于以上的情況，文中采用基于多時間斷面法的電力系統戴維南等值參數計算方法，提出了一種電網在不同頻率下戴維南等值參數表達的新形式。考慮電網中可能存在的大容量整流性負載情況，對一個含三相不控整流負荷的IEEE 9節點簡單系統進行分析，發現其等值節點的戴維南阻抗參數與頻率不存在正相關關系。通過對系統最大諧波功率傳輸能力進行仿真，驗證了以上戴維南等效參數的有效性。

1 基于多時間斷面的電網戴維南參數計算方法

對于第n次諧波，實際電力系統中，在時刻t從任一線性節點向系統看過去，均可把系統看成一個電壓源經過一個阻抗向該負荷節點供電的兩節點系統，如圖1所示。這里取等值節點負荷模型為恒定電阻與恒定電感并聯模型，ZnL的阻抗值僅與考慮的諧波次數有關。

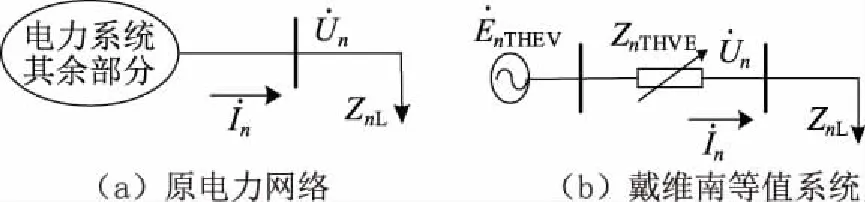
圖1 電力系統戴維南等值

圖1中，對于第n次諧波，各電氣量有如下關系：

(1)

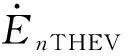
式(1)中選用電壓和電流進行計算，而不沿用文獻[10]中用電壓和功率進行計算，主要是基于以下的考慮：

(1)實際系統中諧波功率的測量較為困難；

(2)在諧波次數較大時，諧波功率和諧波電壓的數值比較小，諧波功率往往達不到基波功率的1%，在采用標幺值進行計算時，功率和電壓就更小了，在計算過程中可能會出現嚴重錯誤。

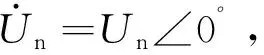
(2)

式中EnTHEV,r、EnTHEV,i分別為戴維南等值電勢EnTHEV的實部和虛部；RnTHEV、XnTHEV分別為戴維南諧波電阻和電抗；In,r、In,i分別為等值節點負荷電流的實部和虛部。

該方程組有2個方程，4個未知數。因此必須再給定兩個方程，一般認為當等值系統內部未發生擾動，僅等值節點側發生較小的擾動時，兩個運行點具有相同的戴維南參數。按照此思路在基態下給等值節點一定大小的擾動，由此得到基態附近的另一個運行點，采集這兩個運行點的數據，該種方法即是使用較為廣泛的多時間斷面法[10-11]。

由式(2)可以得到：

(3)

根據式(3)即可計算出戴維南參數，如式(4)～式(7)所示。

(4)

(5)

(6)

(7)

其中：

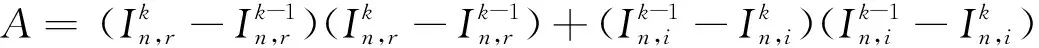
多時間斷面法跟蹤方法基于兩個運行點的戴維南參數相同的假定，因此其跟蹤戴維南參數準確性的關鍵在于領域點的選取，等值節點處的負荷擾動太大，會使擾動后的采集數據與擾動前系統的運行數據偏差較大，計算得出的等值參數誤差也會變大；擾動太小，則存在參數漂移現象，等值結果可能不正確。文中在實際算例中，采用擾動負荷功率的方式，擾動幅度小于2%。

2 算例分析

為探究含電力電子裝置系統的戴維南參數的頻域特性，以含整流裝置的IEEE 9節點簡單系統進行分析。

對于含電力電子裝置的IEEE 9節點系統，建立阻抗解析模型十分困難，如何證明阻抗等值參數的準確性極具挑戰性。

傳統電網中，負荷阻抗減小時，電網阻抗和負荷阻抗逐漸接近，兩者相等時，負荷功率取得最大值，電壓達到崩潰點，這時，負荷阻抗再減小，功率也不再增加，電壓迅速下降。故已有文獻用阻抗模裕度來判斷系統臨界穩定狀態[14]。

考慮某次諧波時，同樣滿足上述的最大功率傳輸定理，阻抗模裕度可以反映系統在該頻率下當前運行狀態離極限傳輸狀態的距離。因此文中采用阻抗模指標的系統最大諧波功率傳輸仿真來驗證戴維南參數等值的準確性。

擴展阻抗模裕度的定義，定義第n次諧波下的阻抗模裕度為：

(8)

當μn取0時，表示在該頻率下系統運行在最大功率點；μn越小，表示系統離極限傳輸功率點越近。

2.1 仿真系統介紹

含整流裝置的IEEE 9節點簡單系統的系統結構拓撲如圖2所示。

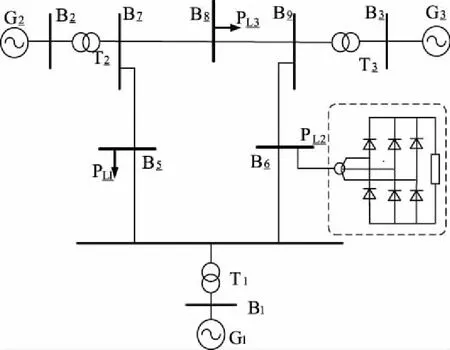
圖2 9節點系統結構圖

BPA暫態仿真程序采用基波相量進行計算，無法計及系統的諧波分析，而PSCAD采用時域分析，基于三相瞬時值進行計算，故采用PSCAD電磁暫態穩定程序作為仿真工具，在PSCAD平臺下搭建系統。

各模型參數大體上參照IEEE 9節點系統中的參數，發電機為同步電機模型，均帶勵磁機，G2帶穩定器，變壓器采用雙繞組變壓器模型，輸電線路采用集中模型。模型參數由BPA暫態仿真模型轉換而來，轉換方法參照文獻[15]，BPA中未給出的參數按照默認值設定，主要參數如表1所示。

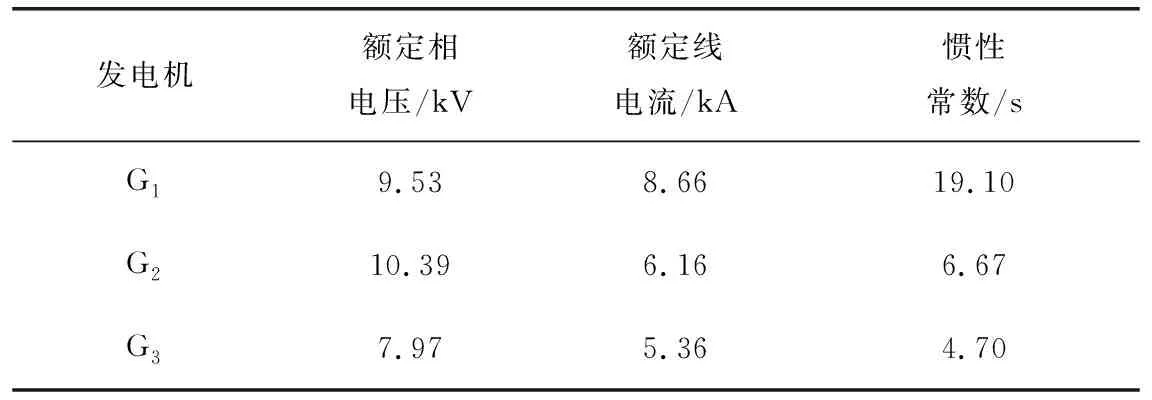
表1 IEEE 9系統主要參數

潮流計算中，各節點負荷均作為節點注入功率處理[10]，文中需要計及諧波分布，顯然不適用。簡便起見，負荷均采用電阻與電感的靜態負荷模型，為了模擬含整流器的情況，母線B6負荷以功率為105+j20(MVA)的三相不控整流負荷代替標準系統中的負荷PL2，整流負荷不考慮濾波，PL1、PL3負荷均為電感、電阻恒定模型，負荷的電阻值和電感值根據標準系統中的參數計算而來，取基準容量為100 MW，基準電壓為額定電壓，負荷的阻抗標幺值如表2所示。

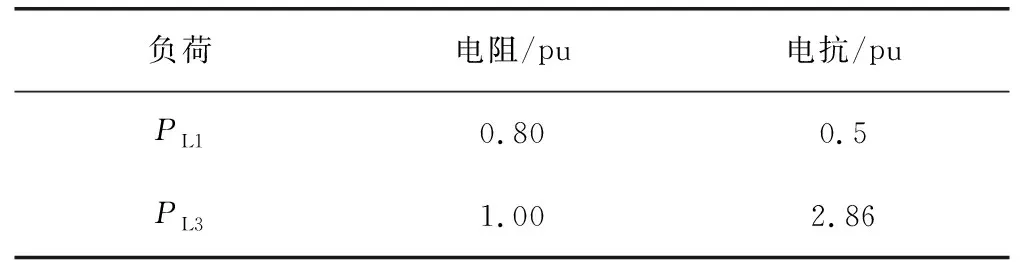
表2 負荷阻抗參數

利用IEEE 9節點系統接入三相不控整流負荷后，負荷母線B6處的波形畸變情況如圖3所示。圖4給出了某一負荷水平下母線B8處電壓、電流和諧波分析情況。由圖可知，系統主要含整數次諧波，不控整流負荷接入母線B6電壓畸變較為嚴重，諧波含量達到了20%。與母線B6相比，母線B8處諧波含量較小。

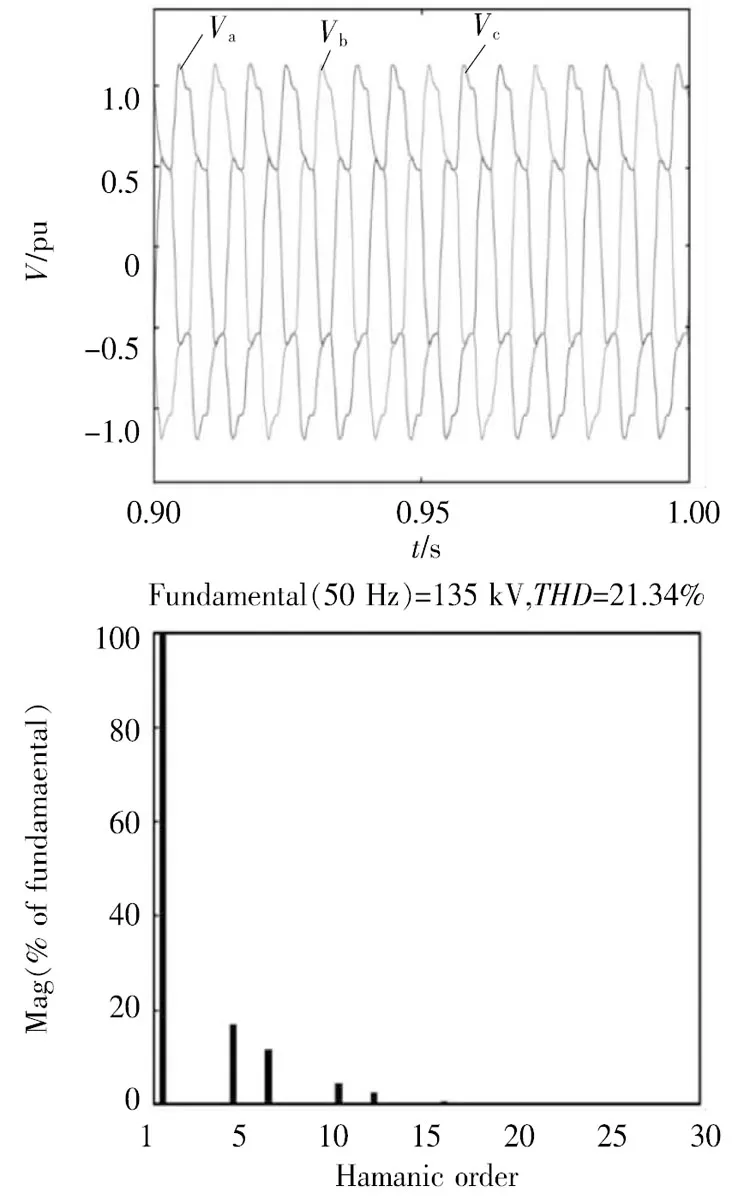
圖3 B6節點處諧波畸變情況

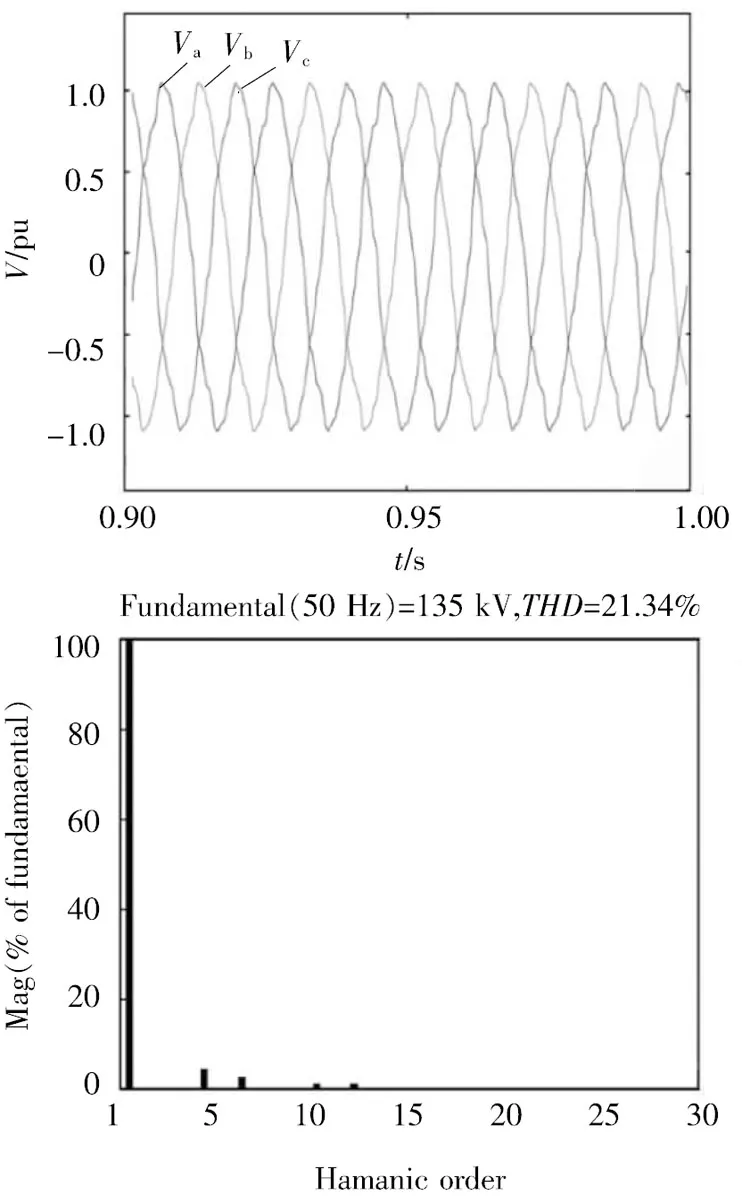
圖4 B8節點處諧波畸變情況

2.2 戴維南等值結果

算例中，選擇從負荷母線B8處進行戴維南等值，采用以上第1節提到的多時間斷面法，已有文獻中忽略了諧波，領域點按照一定程度的功率擾動給定[11]，文中需要計及諧波，故領域點按照等值節點負荷電阻擾動2%，電感保持不變選取，此時負荷側的波動占主導。

三相不控整流負荷的諧波特征次為6k±1 (k=1, 2,3…)，以1, 5, 7, 11, 13次為例進行分析。采用PSCAD自帶的FFT模塊進行傅里葉分解，此模塊采樣1個基頻周波的數據，帶抗混疊濾波器，可以較為準確地輸出整數次諧波的幅值和相位。

戴維南等值參數不是固定不變的，受負荷水平、網絡拓撲、發電狀況、運行模式等因素的影響[13]，文中探究不同負荷水平下電網戴維南等值參數與頻率的關系。

文中采用的阻抗標幺值(R及XL)來表征等值節點負荷水平。圖5給出了不同負荷水平下的戴維南諧波阻抗模。圖5(a)中，負荷節點僅含R支路，改變電阻參數，通過戴維南等值得到了一系列諧波阻抗模。圖5(b)是保持負荷節點電感不變，改變電阻參數得到的諧波阻抗模。圖5(c)則是保持電阻不變，改變電感參數得到的諧波阻抗模。

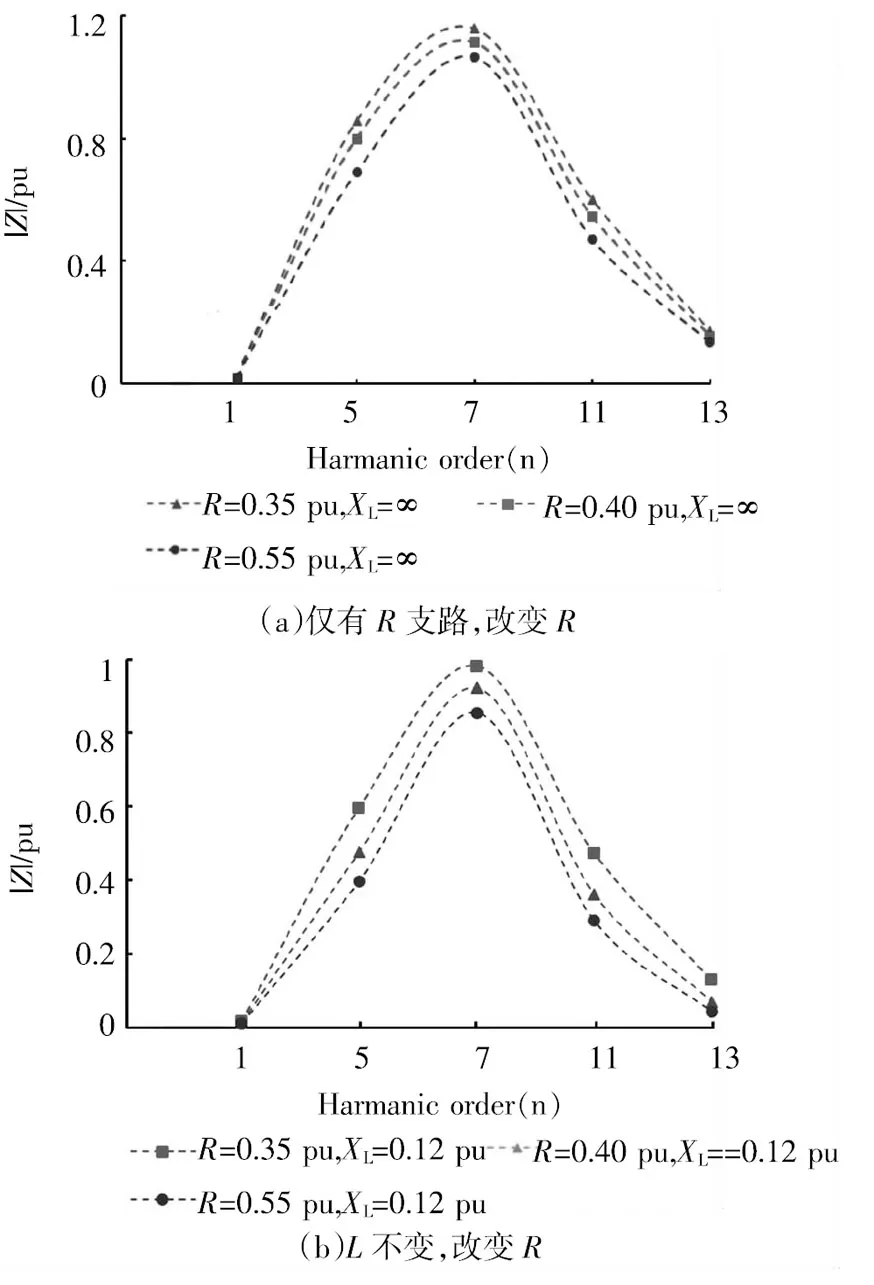
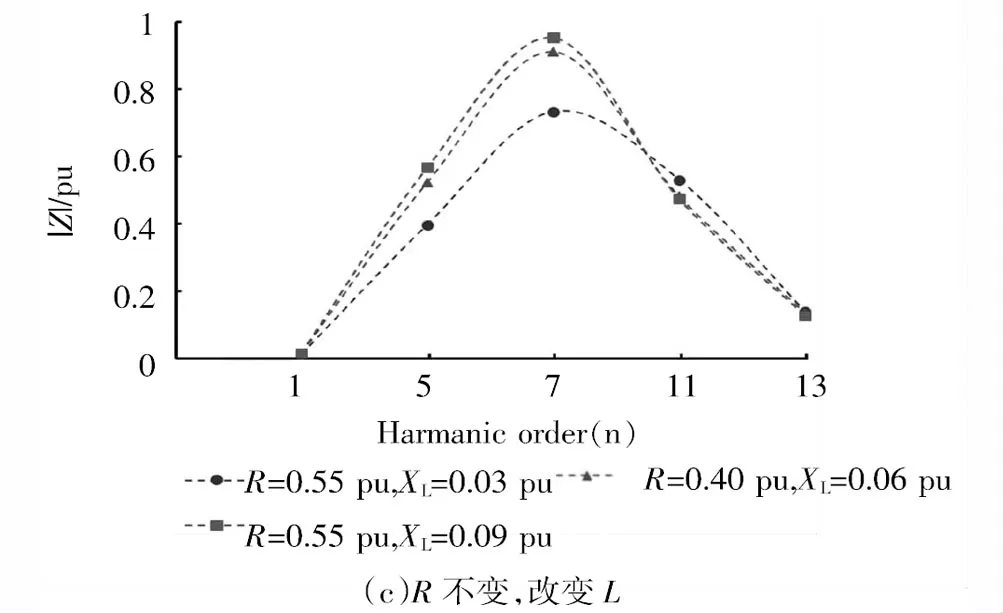
圖5 戴維南等值結果

從圖5可以發現，改變等值節點負荷水平，諧波阻抗變化比基波阻抗變化稍大，但總體來說變化較小。盡管節點負荷水平不同，含大功率整流性裝置的電網其戴維南等效參數的阻抗模值都具有隨頻率先增大后減小的非線性關系。這與傳統電網戴維南等效阻抗X/R比值持續增大的情況完全不同。對于本算例來說，阻抗模最小值出現在基波頻率下，大致為0.01 pu左右。阻抗模值最大值均出現在第7次諧波頻率下，大致為0.8 pu～1 pu左右。

同時僅考慮某一諧波頻率下的戴維南參數，發現保持電感不變減小電阻值，即增大等值節點負荷，諧波阻抗模逐漸增大；保持電阻不變，增大電感值，5次、7次處諧波阻抗模逐漸增大，但11次、13次處增大趨勢不明顯。

2.3 結果驗證

等值節點負荷水平為R=0.55 pu，XL=0.06 pu時(即負荷水平一)，戴維南阻抗模與負荷阻抗模的取值如表3所示。

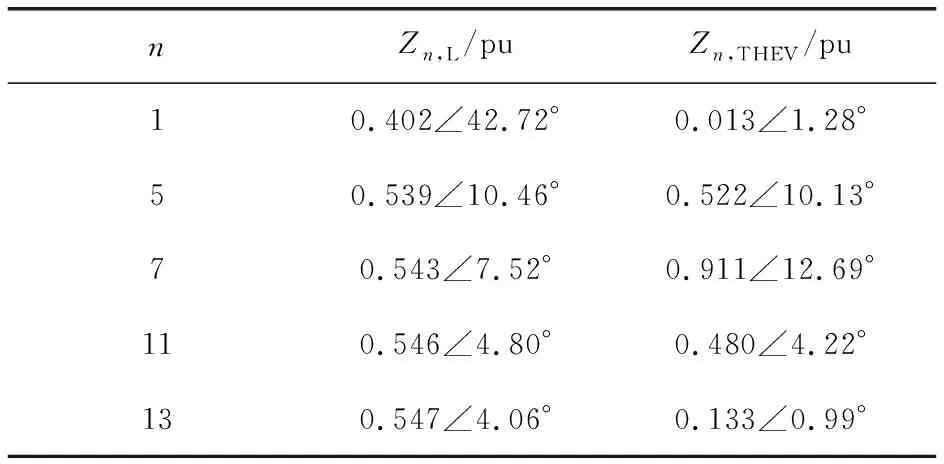
表3 負荷水平一時負荷阻抗模及戴維南阻抗模

由表3可知，n=5時，Zn,L和ZnTHEV模值近似相等。按照阻抗模裕度指標來檢驗5次下諧波阻抗的準確性，保持等值節點負荷電感不變，改變等值節點電阻，n=5時有功功率、戴維南參數及阻抗模裕度指標如表4和圖6所示。

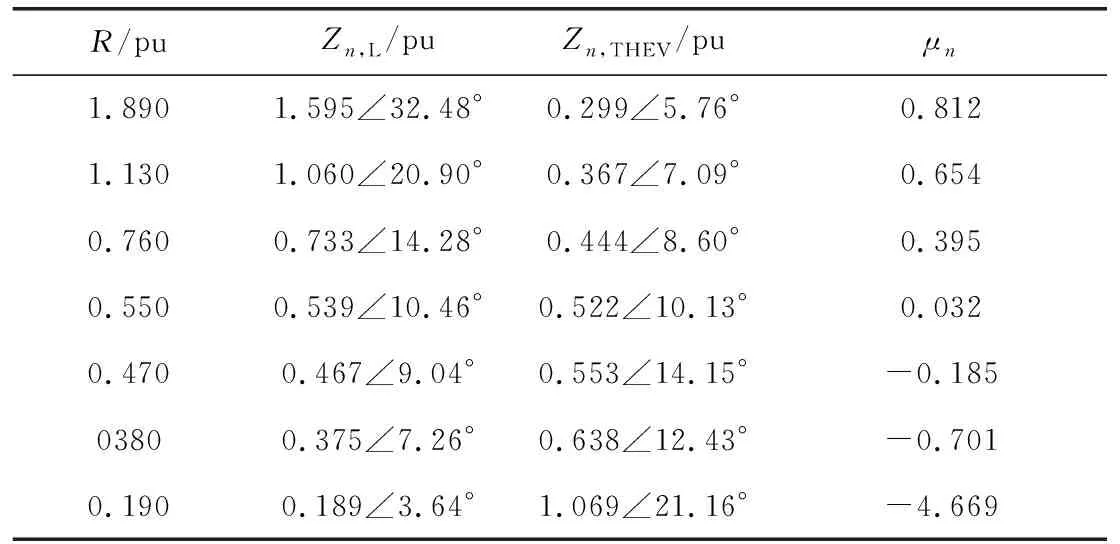
表4 n=5時，不同負荷水平下的阻抗模指標

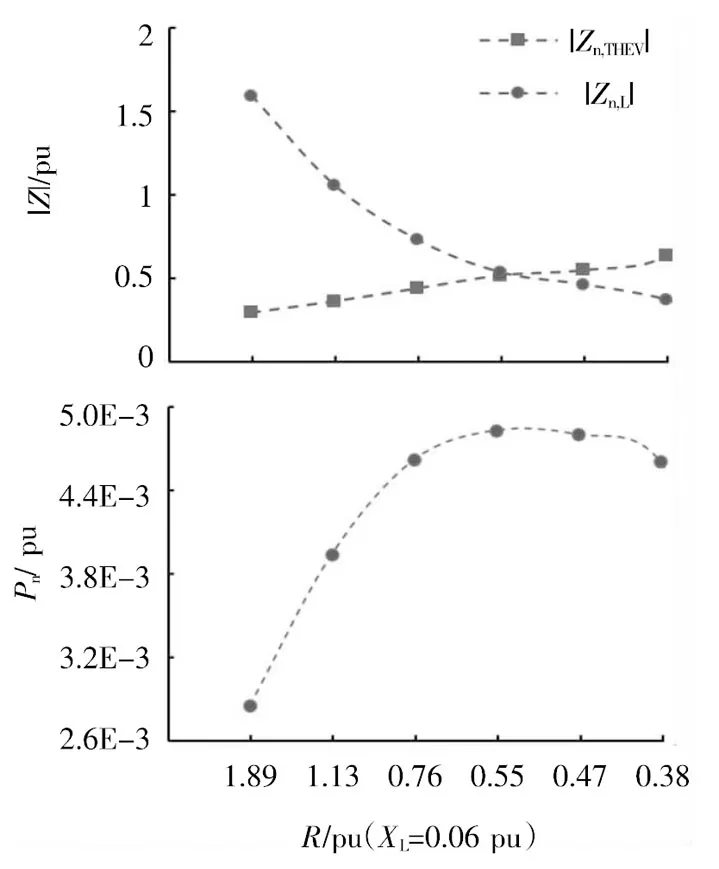
圖6 n=5時，不同負荷水平下的戴維南參數

僅考慮n=5時，隨負荷水平增加，負荷阻抗模和諧波阻抗模逐漸接近，阻抗模裕度μn減小，當負荷水平為R=0.55 pu，XL=0.06 pu時，μn為很小的正數0.032，線路傳輸的該次有功功率達到最大值，達到電壓崩潰點。這時，負荷水平再增加，阻抗模裕度由正數變為了負數，有功功率不再增加。

在等值節點負荷水平為R=0.95 pu，XL=0.12 pu時(即負荷水平二)，戴維南等值阻抗模與負荷阻抗模的取值如表5所示。

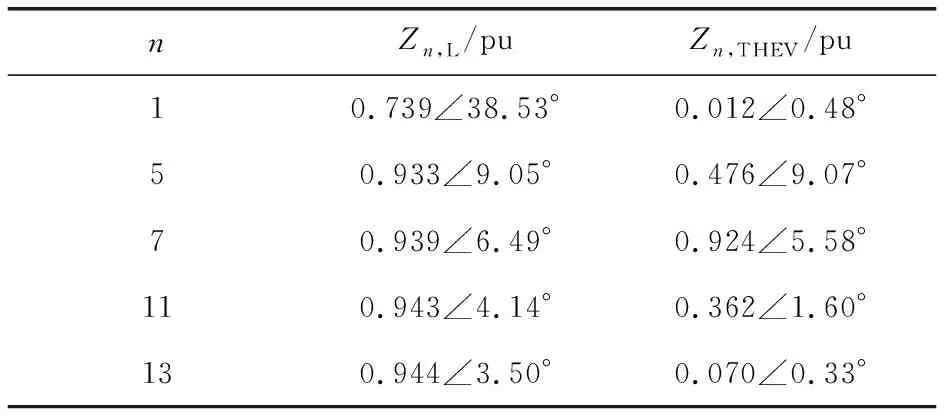
表5 負荷水平二時負荷阻抗模及戴維南阻抗模

n=7時，Zn,L和ZnTHEV模值近似相等。同樣保持等值節點負荷電感不變，改變等值節點電阻，n=7時有功功率、戴維南參數及阻抗模裕度指標如表6及圖7所示。

當負荷水平為R=0.95 pu，XL=0.12 pu時，線路傳輸的該次有功功率達到最大值。

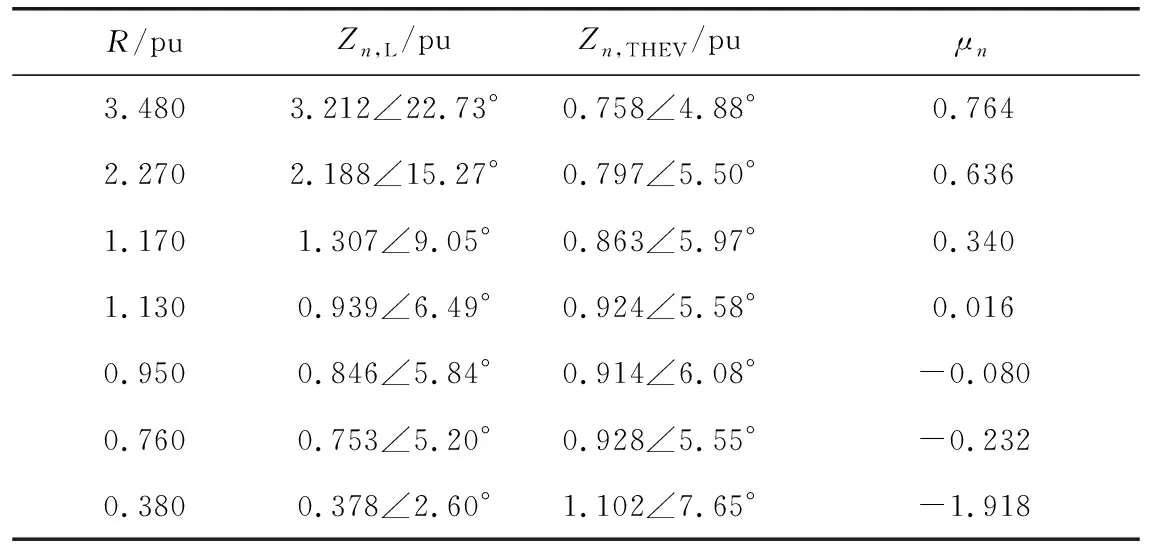
表6 n=7時，不同負荷水平下的阻抗模裕度

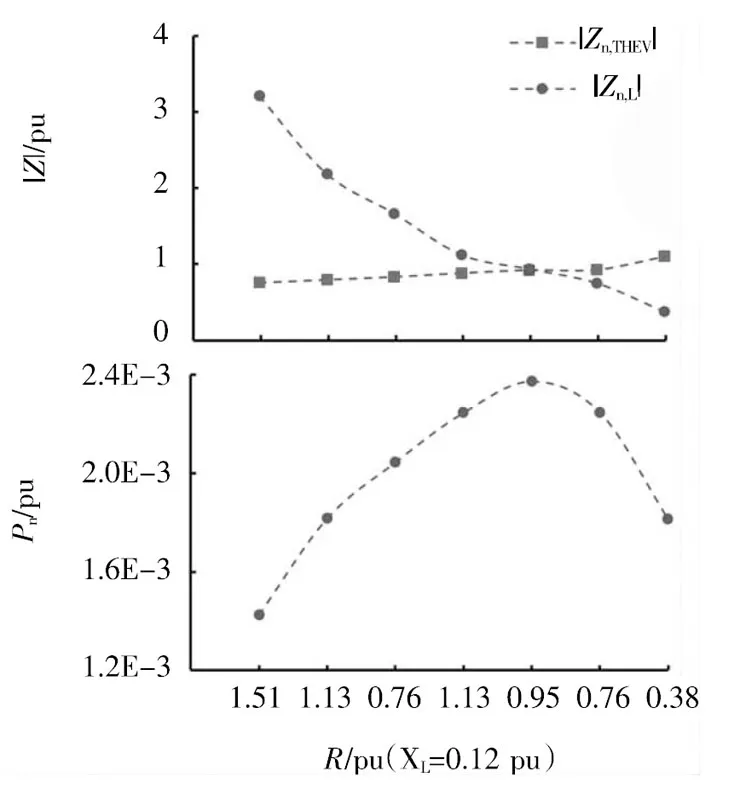
圖7 n=7時，不同負荷水平下的戴維南參數

在等值節點R=0.55 pu，XL=0.03 pu的負荷水平下(即負荷水平三)，諧波阻抗模與負荷阻抗模的取值如表7所示。

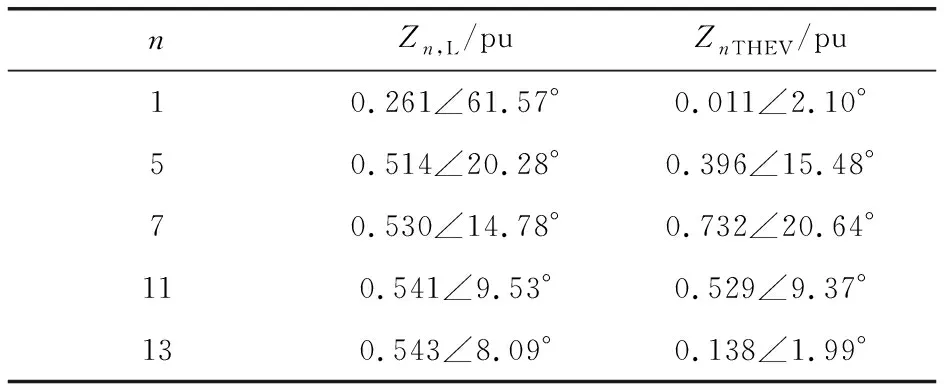
表7 負荷水平三時負荷阻抗模及戴維南阻抗模

n=11時，Zn,L和ZnTHEV模值近似相等。因此保持等值節點負荷電感不變，改變等值節點電阻。n=11時有功功率、戴維南參數及阻抗模裕度指標如表8和圖8所示。

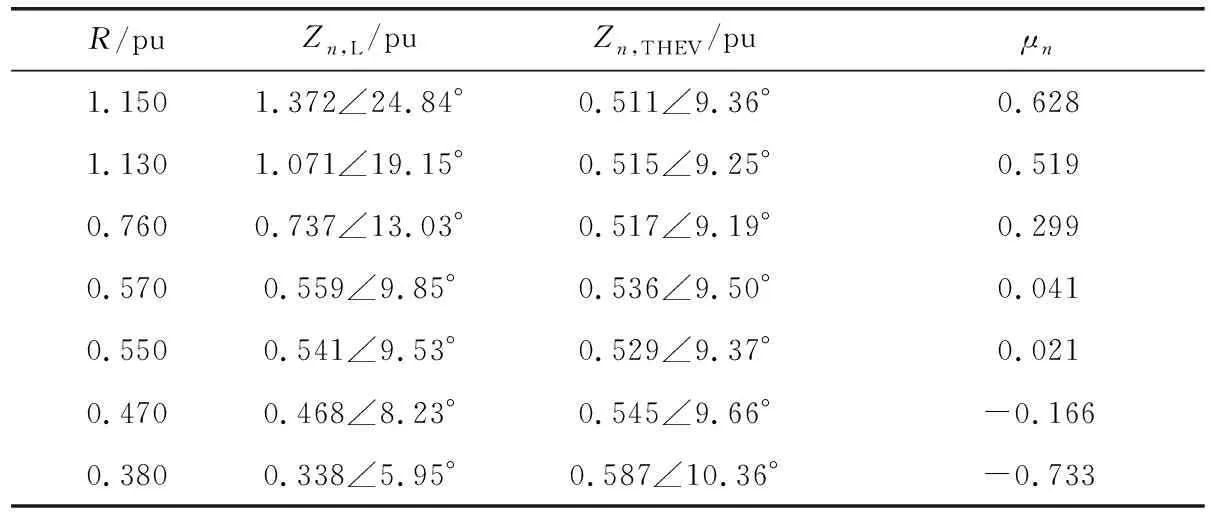
表8 n=11時，不同負荷水平下的阻抗模裕度

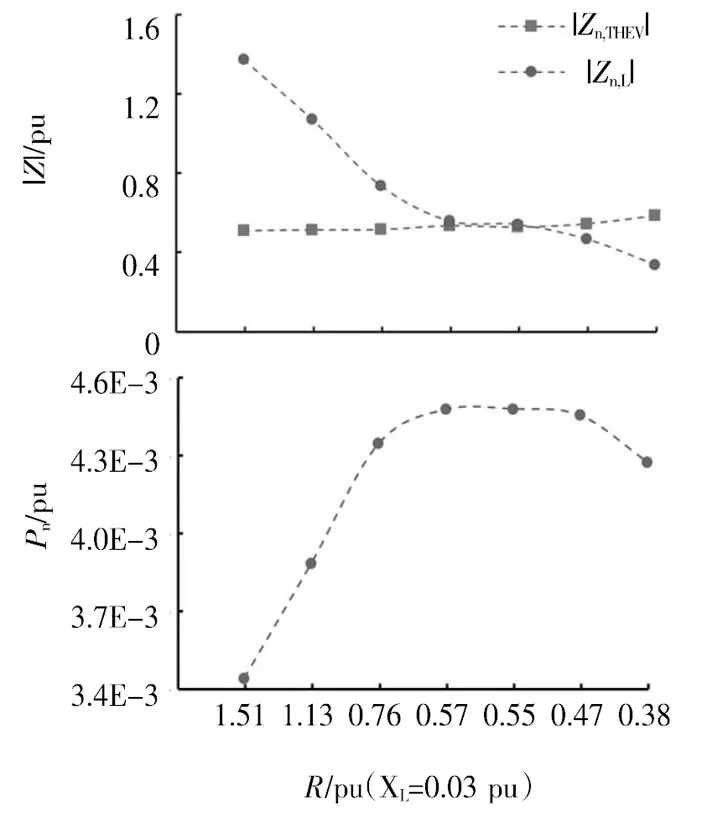
圖8 n=11時，不同負荷水平下的戴維南參數

由圖8可知，Zn,L和ZnTHEV在R=0.55 pu，XL=0.03 pu時達到負荷匹配狀態，傳輸的第11次諧波功率達到最大。

在等值節點R=0.20 pu，XL=∞的負荷水平下(即負荷水平四)，戴維南等值阻抗模與負荷阻抗模的取值如表9所示。

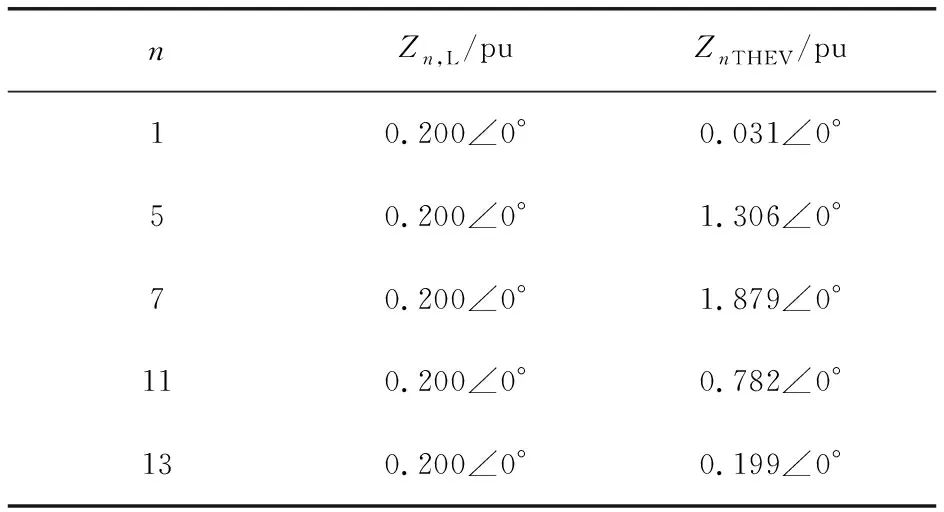
表9 負荷水平四時負荷阻抗模及戴維南阻抗模

n=13時，Zn,L和ZnTHEV模值近似相等。因此僅改變等值節點電阻參數，n=13時有功功率、戴維南參數及阻抗模裕度指標如表10和圖9所示。

由仿真結果可知，在R=0.20 pu，XL=∞時，諧波阻抗模與負荷阻抗模接近，μn基本為0，此時，系統傳輸的第13次諧波功率取得最大值。

從以上阻抗模指標的仿真結果可以看出，在研究的系統中，戴維南阻抗與頻率為非正相關關系，各次諧波頻率下的阻抗模值分別如圖6～圖9所示。

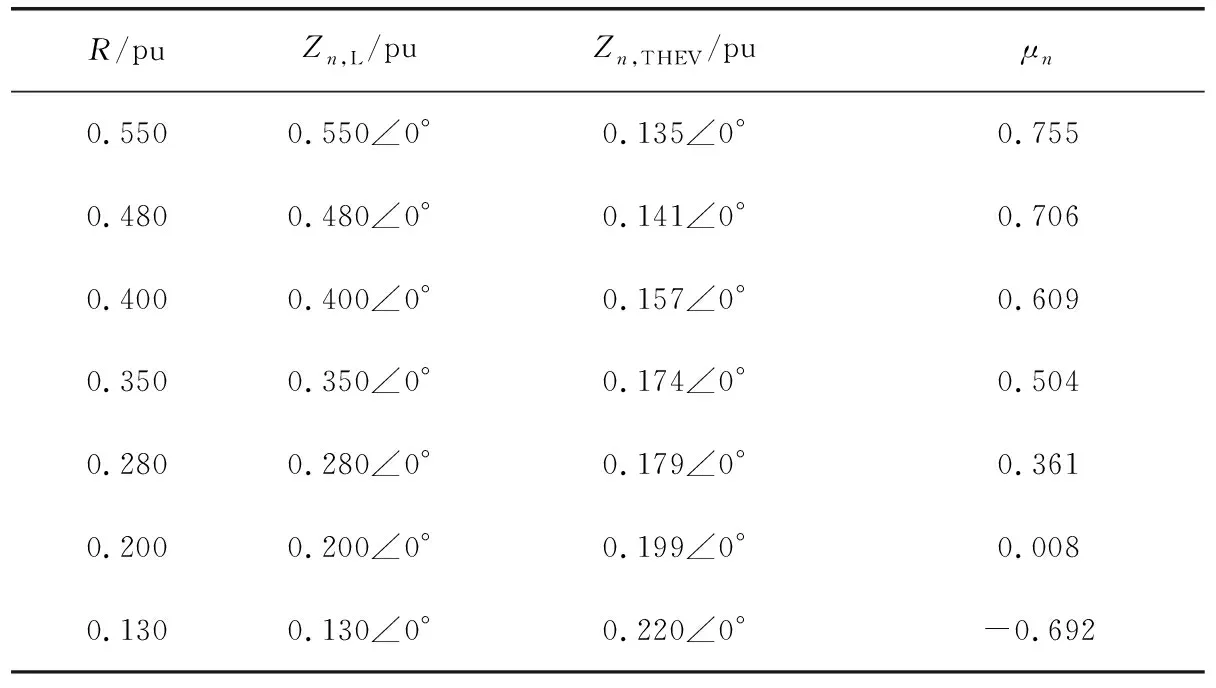
表10 n=13時，不同負荷水平下的阻抗模裕度

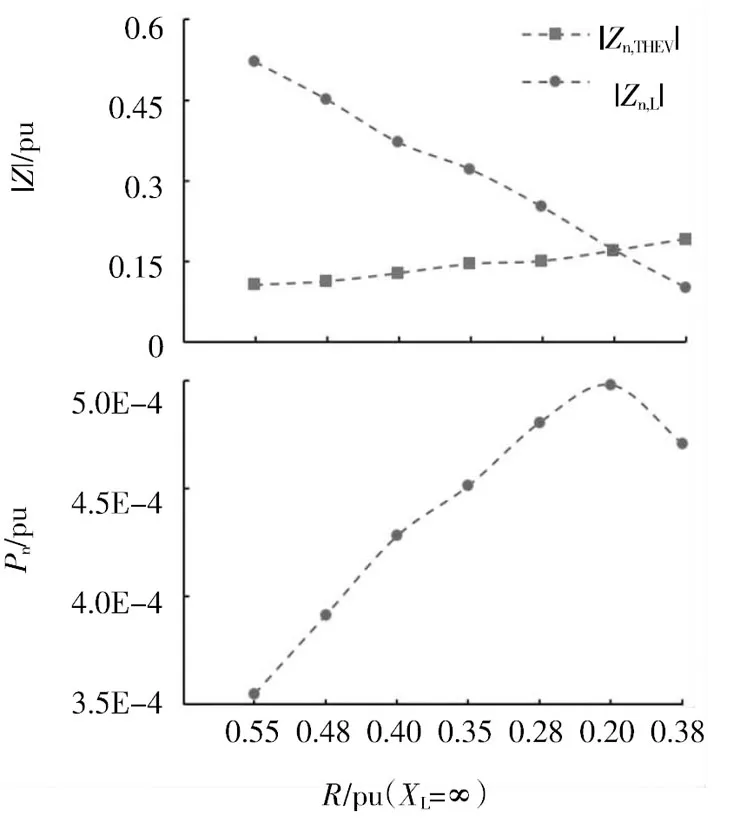
圖9 n=13時，不同負荷水平下的戴維南參數

綜合以上分析，可以發現，該系統阻抗模值在7次諧波頻率下取得最大值，與第2節中的分析結果完全一致。因此，分析中采用多時間斷面法得到的戴維南等值結果是準確的，戴維南阻抗與負荷阻抗匹配時，在對應頻率下的諧波功率取得最大值。

3 結束語

考慮到電力電子裝置的高滲透給電網帶來的影響，提出采用基于多時間斷面法的電力系統戴維南等值參數計算方法，給出了電網不同頻率下戴維南等值參數表達通過對含整流裝置的IEEE 9節點簡單系統進行分析，發現其等值阻抗與頻率為非正相關關系。分析結果通過基于阻抗模指標的電力系統最大諧波功率傳輸能力進行了驗證。所提出的等值算法能夠應用于不同頻率下的戴維南參數計算，更好地反映實際電網阻抗變化情況，具有一定的實用價值。