考慮P2G的電-氣綜合能源系統分布式最優能量流*

張海峰，汪一波

(北京大學 動力中心，北京 100871)

0 引 言

隨著化石能源的不斷消耗，能源危機與環境污染問題日益突出，如何實現能源的高效、清潔利用是國內外研究的熱點問題[1]。2015年和2017年，我國兩次提出“建設全球能源互聯網”的偉大戰略目標，標志著電網向能源互聯網演進的趨勢[2]。能源互聯網借助多網融合及信息互聯網的優勢，大大提升了能源調度運行的靈活性，成為提高能源系統對風電消納能力的重要技術手段[3]。

電-氣綜合能源系統是能源互聯網的重要組成部分。作為最優潮流的延伸，最優能量流(Optimal Energy Flow, OEF)是用于分析電-氣綜合能源系統安全經濟運行的有效工具[4]，國內外學者對該問題展開了大量的研究，主要包括：電-氣綜合能源系統OEF的高效求解算法[5-6]，電-氣綜合能源系統OEF的凸優化建模[7]、計及不確定性因素的概率OEF建模技術[8-9]、電-氣綜合能源系統能量流的暫態特性[10]等方面。但是，上述研究均沒有考慮到電轉氣(Power to Gas, P2G)裝置的接入對OEF的影響。近年來P2G技術發展迅速，電網與天然氣網之間的耦合改變了僅限于燃氣輪機的現狀，電網和天然氣網之間可實現能量的雙向流動[11]，大大提升了電-氣綜合能源系統的運行靈活性。

在含有P2G裝置的電-氣綜合能源系統協調運行研究領域，研究多集中于新能源消納[12]、市場化運營[13]、可靠性評估[14]、OEF模型及求解[15]等領域。其中，在含有P2G裝置的OEF計算方面，研究還處于初級階段。此外，對模型的求解通常基于集中式優化，這需要通過調度中心收集并處理全局信息。隨著分布式電源及其他可控設備的高滲透率接入，集中式優化對通信、存儲、計算等資源的要求將難以得到滿足；此外，在電力系統和天然氣系統歸屬于不同利益主體的情況下，各主體信息將歸其自身所有，全局信息的獲取將成為制約集中式優化發展的最大瓶頸。

近年來，分布式優化領域取得了豐碩的研究成果。經典的方法有Benders分解法[16]，Dantzig- Wolfe 分解法[17]和拉格朗日松弛分解法[18]和交替方向乘子法(Alternating Direction Multiplier Method, ADMM)[19]等。其中，ADMM的核心思想是將大問題分解成若干個子問題，按順序對幾組不同變量進行交替迭代，最終達到共同收斂，其在最優潮流的分布式計算中得到了廣泛的應用。

根據上述分析，提出了一種考慮P2G的電-氣綜合能源系統分布式最優能量流模型及分布式求解算法。首先對P2G技術進行簡單的概述，其次建立電-氣綜合能源系統的OEF模型，并通過ADMM算法實現模型的分布式求解，最后在IEEE-39節點電網和修改的比利時20節點天然氣網組成的電-氣綜合能源系統進行算例分析。

1 P2G技術概述

電轉氣技術是指電力轉化為氣體燃料的技術。現有技術手段下主要指電轉氫氣技術和電轉甲烷技術。電轉氫氣是通過電解水，從而產生氫氣和氧氣。具體的化學方程式如下：

(1)

電轉甲烷則是在電轉氫氣后，進一步進行氫轉甲烷過程。在加溫加壓的環境下，氫氣和二氧化碳發生反應，生成甲烷和水。具體的化學方程式如下：

(2)

電轉氣過程中，輸入電功率PP2G(單位是MW)與產生天然氣流量wP2G(單位是m3)的關系為：

(3)

式中ηP2G表示P2G設備的轉換效率，單位是MW/ m3；GHV表示天然氣的熱值。

現階段，電轉甲烷的綜合能源轉化效率只有45%～60%，而電轉氫氣的能量轉換效率可達到75%～85%[5]。但是相比氫氣，甲烷的單位能量密度較高，且可直接注入現有天然氣管道進行儲存和傳輸，將有效促進電網和天然氣網雙向互動。同時，在可再生能源迅速發展和節能減排壓力凸顯的今天，利用富余的清潔電源制成氫氣，再與CO2反應合成甲烷，對環境與經濟都具有一定的現實意義。目前，德國已經將P2G技術(指電轉甲烷)應用于實際，于2012年建成電轉氣廠試點，未來電轉甲烷技術應用前景廣闊。

據此，主要圍繞電轉甲烷技術對電-氣聯合網絡相互影響關系進行研究，故文中提及的P2G均指電轉甲烷。

2 電-氣綜合能源系統OEF模型

本章建立電-氣綜合能源系統的OEF模型，該模型以各電力系統和天然氣系統供能主體出力、能量耦合環節能量輸入及分配系數為決策變量，以系統總體運行成本為優化目標，綜合考慮電力系統、天然氣系統及能量耦合環節運行約束。

2.1 目標函數

對于電力系統，其成本函數為[20]：

(4)

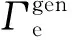
對于天然氣系統，其成本函數為：

(5)

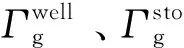
由于Ce和Cg均為成本的表達式，其量綱相同，均是$，因此以直接相加的形式表示本模型的目標函數，其表達式為：

minC=min(Ce+Cg)

(6)

2.2 約束條件

2.2.1 電力系統約束

(1)功率平衡約束。

對于電力系統中某個節點i，需滿足[21]：

(7)

式中Vi和δi分別表示節點i的電壓幅值和相角；其中Vi單位是V，δi無量綱；δij=δi-δj；Gij+Bij表示節點導納矩陣Y中相應的元素，單位是Ω-1；j∈i表示節點j是節點i的關聯節點；Pi表示節點i的凈注入功率，單位是MW，其值等于節點i產生的功率減去消耗的功率，假設節點i同時存在非耦合發電機、風電機組、電-氣耦合燃氣機組、P2G機組以及電負荷，則Pi的表達式為：

(8)

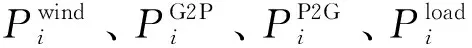
(2)電力系統安全約束。

電力系統安全約束包括節點電壓約束、線路有功潮流約束，具體如下：

(9)

(10)

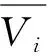
(3)電源約束。

對于非耦合發電機，需要其滿足出力上下限約束，即：

(11)

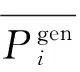
2.2.2 天然氣系統約束

(1)氣流量平衡約束。

與電力系統節點功率平衡約束類似，天然氣系統某一節點應滿足節點功率平衡約束，該約束通常以氣流量的形式表示：

(12)

式中qi表示節點i的凈注入流量，單位是m3；qij表示管道ij的穩態流量，單位是m3；u(i)表示以i為首端節點的末端節點集合；v(i)表示以i為末端節點的首端節點集合。qij的表達式為：

(13)

(14)

式中cij表示與管道效率、溫度、長度、內徑、壓縮因子等有關的常數；πi表示節點i的壓力，單位是Pa。

對于qi，假設節點i同時存在氣井、儲氣裝置、P2G機組、電-氣耦合燃氣機組以及氣負荷，則qi的表達式為：

(15)

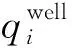
(16)

(2)天然氣系統安全約束。

天然氣系統安全約束包括節點壓力約束和管道流量約束，具體如下：

(17)

(18)

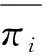
(3)氣源約束。

對于氣井，需要保證其儲存的天然氣量在一定范圍內，即：

(19)

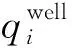
對于儲氣裝置，其既可以在氣負荷較大時作為源提供天然氣，也可在氣負荷較小時作為荷對多余的天然氣進行存儲，其約束包括：

(20)

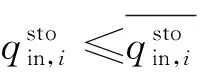
(21)

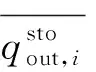
(4)加壓站約束。

天然氣在傳輸過程中會產生能量損失，因此天然氣網一般會配置加壓站。加壓站消耗的能量通常由燃氣輪機來提供，圖1為燃氣輪機驅動的壓縮機示意圖。

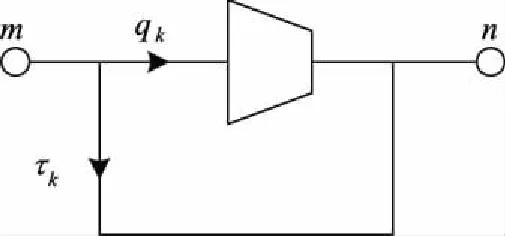
圖1 燃氣輪機驅動的壓縮機

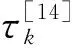
(22)

(23)

(24)

式中Hk表示壓縮機k消耗的電能，單位是MW；αk、βk和γk表示壓縮機k能量轉換效率常數，單位分別是m3、m3/MW、m3/MW2；Bk表示與壓縮機k效率、溫度、天然氣熱值有關的常數；qk表示流過壓縮機k的流量，單位是m3；Zk表示與壓縮機k壓縮因子和天然氣熱值有關的常數；κk表示加壓站壓縮機k的加壓比，其需要滿足約束：

(25)

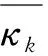
(5)氣流量-能量(功率)約束。

在天然氣網中，天然氣作為能量的載體在管道中流動，天然氣流量與天然氣功率之間的關系表達式為：

Pg=SHHVqg

(26)

式中Pg表示天然氣功率，單位是MW；qg表示天然氣流量，單位是m3；SHHV表示天然氣高熱值，單位是MW/m3。式(26)可用于天然氣流量與天然氣功率的換算。

2.2.3 能量耦合約束

在電-氣綜合能源系統的OEF模型中，電力系統和天然氣系統之間主要通過燃氣機組和P2G機組耦合，能量耦合約束包括能量輸入-輸出約束和裝置運行約束。

(1)能量輸入-輸出約束。

電-氣耦合燃氣機組和P2G機組的能量輸入-輸出約束可表示為：

(27)

(28)

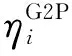
(2)裝置運行約束。

電-氣耦合燃氣機組和P2G機組的裝置運行約束可表示為：

(29)

(30)

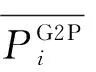
3 OEF模型的分布式求解方法

本章首先說明ADMM算法的基本原理，之后將ADMM算法應用到電-氣綜合能源系統的OEF模型求解中，實現模型的分布式求解。

3.1 交替方向乘子法ADMM

ADMM的核心思想是將大問題分解成若干個小的子問題后，按順序對幾組不同變量進行交替迭代，從而求解計算，并更新相應的對偶變量，最終達到共同收斂。其標準形式如下：

minf(x)+g(z)

(31)

Axc+Bzc=C

(32)

式(31)中，f()和g()為2個凸函數；x、z為兩組變量。式(32)表示不同優化問題之間的耦合關系，xc、zc為共享變量；x∈Rn，z∈Rm，xc∈Rp、zc∈Rp，A∈Rp×p，B∈Rp×p，C∈Rp。

構造增廣拉格朗日函數：

Lρ(x,z,λ)=f(x)+g(z)+λT(Axc+Bzc-C)+

(33)

式中Lρ()為增廣拉格朗日函數；λ為對偶變量；ρ>0為懲罰系數。

第g+1次更新迭代的標準格式為：

(34)

ADMM算法收斂判據由兩部分組成：

(35)

式中ξ(g+1)和μ(g+1)分別為第g+1次迭代計算后原始殘差和對偶殘差；εpri和εdual分別為原始殘差和對偶殘差的容忍上限。

3.2 基于ADMM的模型求解算法

對于建立的OEF模型，電力系統和天然氣系統的目標函數分別如式(4)和式(5)所示，兩目標函數均為凸函數，其和完全符合式(31)的形式；同時，式(27)和式(28)構建了兩系統之間的聯系，首先，將式(27)和式(28)改寫為矩陣的形式：

(36)

通過簡單的整理，即將式(27)和式(28)改寫為式(32)的形式，因此，建立的電-氣綜合能源系統的OEF模型可實現分布式求解。

4 算例分析

4.1 算例描述

采用IEEE-39節點電力系統和修改的比利時20節點天然氣系統組成的電-氣綜合能源系統進行算例分析，具體網架結構如圖2所示，IEEE-39節點電力系統具體參數由 Matpower 4.1 提供，比利時 20 節點天然氣系統參數參考文獻其具體參數可參見文獻[22]。所提優化策略通過Matlab編程進行求解，采用的系統配置為Intel(R) Core(TM) i7-7700 CPU 3.60 GHz，16 GB內存。

4.2 準確性及高效性分析

為驗證所提的電-氣綜合能源系統的OEF模型及求解方法的準確性，分別采用統一建模集中式優化以及基于ADMM的分布式優化對圖2所示系統進行求解。圖3顯示了兩種求解方法下電力系統節點電壓和天然氣系統的節點壓力的對比情況。從圖中可以看出，電力系統節點電壓的相對誤差絕對值均不超過3%，天然氣系統節點壓力的相對誤差絕對值均不超過5%，均在誤差允許的范圍內，進而驗證了該分布式優化求解的準確性。

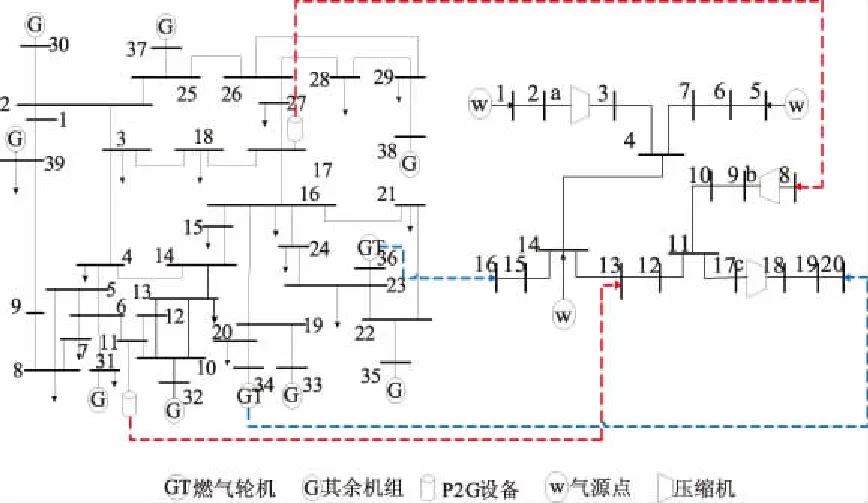
圖2 電-氣聯合網絡網架結構

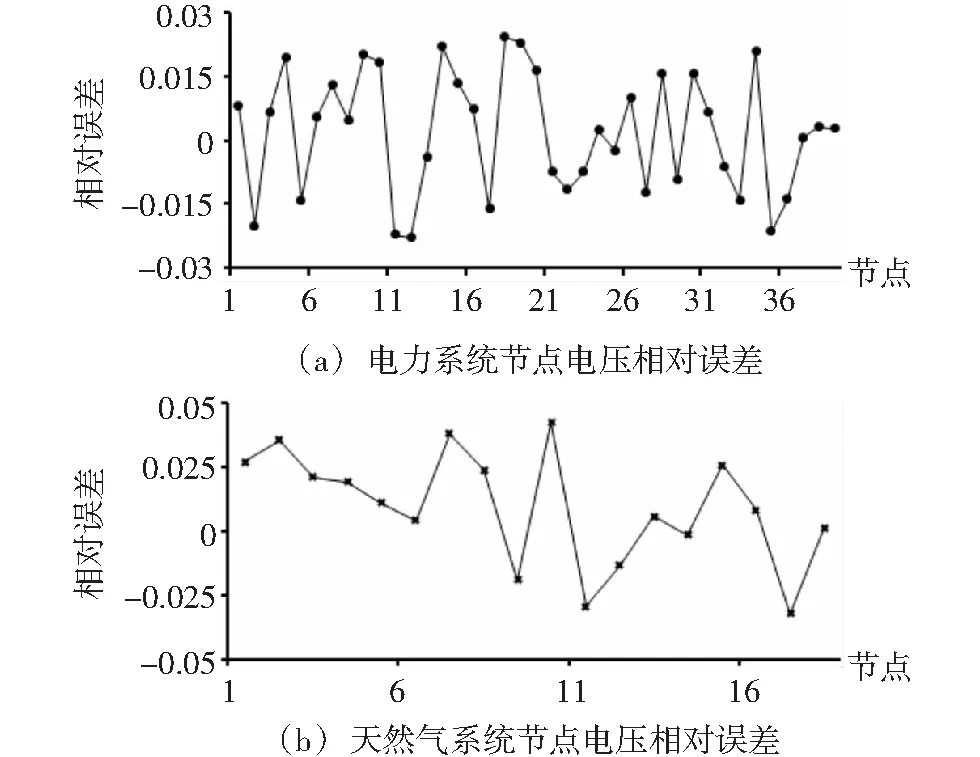
圖3 兩種求解方法下計算結果

計算效率方面，表1顯示了統一建模集中式優化以及分布式優化的計算時間。從表中可以看出，無論采用CPLEX求解器或是Gurobi求解器，文中基于ADMM的分布式優化求解算法在計算效率方面均有較為明顯的優勢。

表1 不同方法求解的效率對比

4.3 P2G的風電消納能力分析

為驗證含P2G的綜合能源系統的風電消納能力，設計了以下三種場景進行仿真分析：

場景1：無電-氣耦合燃氣機組和P2G機組接入綜合能源系統；

場景2：電-氣耦合燃氣機組接入綜合能源系統，P2G機組不接入綜合能源系統；

場景3：電-氣耦合燃氣機組和P2G機組均接入綜合能源系統。

三種場景下的風電消納情況如圖4所示。

圖4 三種場景下的風電消納情況

由圖4可以看出，在三種情景中，情景3在各個時段均實現了風電的最大化消納。這是由于考慮P2G接入后，原電網中不能消納的風電部分，能夠轉換為天然氣，并輸入天然氣網供使用，提高了風電的消納量。同時，雖然場景2不能實現富余風能向天然氣網外送，但其風電消納能力依然高于場景1，這是由于在場景2中，電-氣耦合燃氣機組的接入有助于減輕電力系統部分線路的擁塞情況，使得在滿足線路潮流約束的情況下，更多的風電通過輸電網絡傳送至不同節點的負荷，大大提升的風電的消納能力。

4.4 系統單獨優化與分布式聯合優化的經濟性分析

在4.3節的三種場景中，場景1中電力系統和天然氣系統之間不存在耦合，因此其優化結果為兩系統分別優化的計算結果之和；場景2和場景3中存在兩系統之間的耦合，因此可采用所提的ADDM算法對模型進行分布式求解。場景1的單獨優化與場景2(場景3)的分布式優化結果如圖5所示，表中，用E、G和T分別代表電力系統、天然氣系統和總系統的成本，用1、2和3分別代表場景1、場景2和場景3。

場景3中的能源轉化裝置多于場景2和場景1，而在能源轉化的過程中存在轉化率的問題，但是，從圖5中可以看出，場景3中的電力系統、天然氣系統和總系統的成本均低于場景1和場景2。這是由于一方面場景3有利于風電的消納，從而減少了化石能源的消耗，進而降低了系統的運行成本；另一方面，場景3中由于大量耦合裝置的接入，有利于提高系統運行的靈活性，電力系統中更趨向于開啟成本較低的機組，而天然氣系統更趨向于調用更經濟的氣井和儲氣裝置。因此，雖然場景3中耦合裝置的增多會存在能源利用率下降的問題，但其優越的風電消納能力和運行靈活性仍可保證其運行的經濟性。

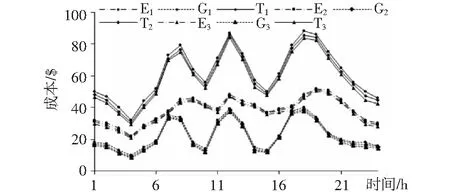
圖5 不同場景下的運行成本

5 結束語

提出了一種考慮電轉氣的電-氣綜合能源系統分布式最優能量流模型及分布式求解算法。通過理論推導、仿真分析，可以得出以下結論：

(1) 電-氣綜合能源系統可以起到減輕電力線路擁塞的關鍵作用，通過將電力系統中的風能外送至天然氣系統，大大提高了風電消納率；

(2) 含有P2G的電-氣綜合能源系統有利于提高系統運行的靈活性，充分消納風電，可大大提升系統運行的經濟性；

(3) 提出的基于ADMM的模型求解算法可在保證計算精度的條件下，大大提高計算的效率。