源于教材練習題的變式探究

滿延福

教材中的練習題一般都具有基礎性與代表性的特點，許多練習題、習題、期末測試題、中考試題均源于教材中練習題、習題的改編或變式，在教學中正確引導對原題進行適當的變式拓展，對發揮學生的潛力，將有助強化學生基礎，培養學生發現問題、分析問題、解決問題的能力。現就湘教版初中數學八年級下冊的一道練習題為例進行說明，本文將與讀者共賞。

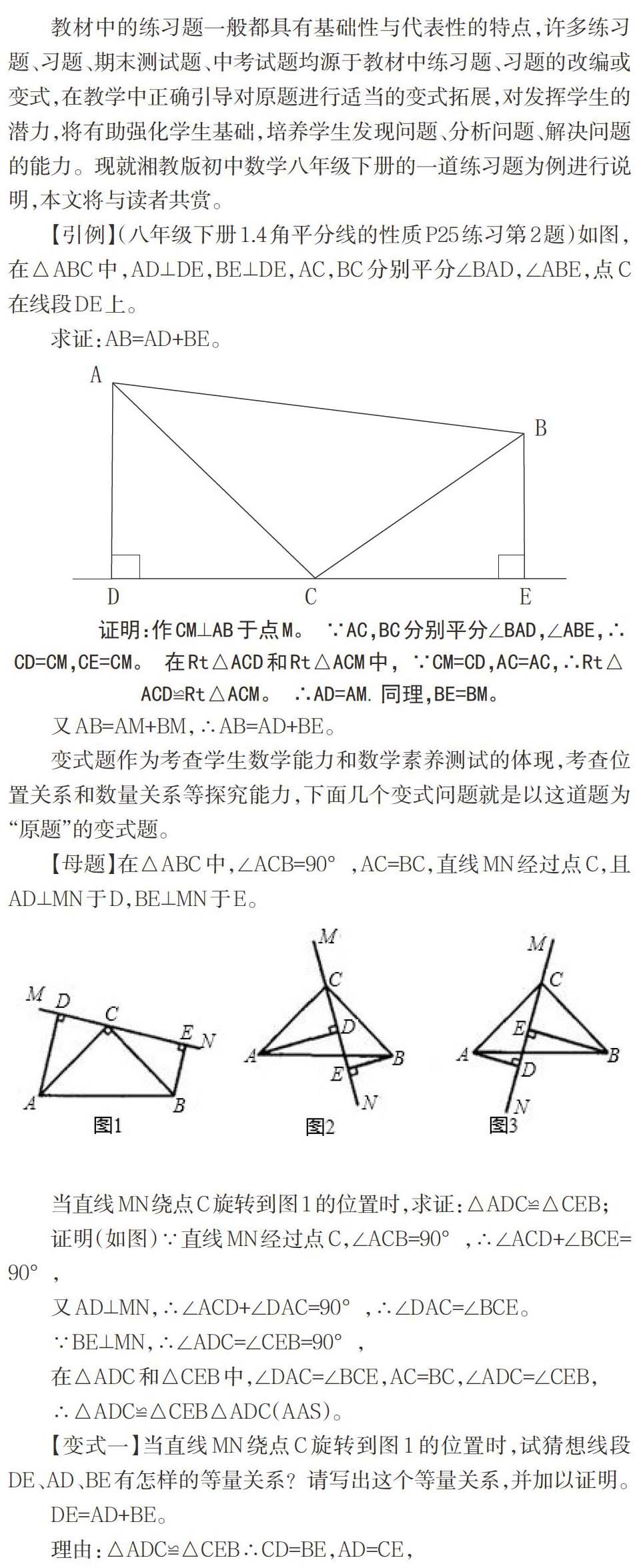
【引例】（八年級下冊1.4角平分線的性質P25練習第2題）如圖，在△ABC中，AD⊥DE，BE⊥DE，AC，BC分別平分∠BAD，∠ABE，點C在線段DE上。

求證：AB=AD+BE。

證明：作CM⊥AB于點M。 ∵AC，BC分別平分∠BAD，∠ABE，∴CD=CM，CE=CM。 在Rt△ACD和Rt△ACM中， ∵CM=CD，AC=AC，∴Rt△ACD≌Rt△ACM。 ∴AD=AM.同理，BE=BM。

又AB=AM+BM，∴AB=AD+BE。

變式題作為考查學生數學能力和數學素養測試的體現，考查位置關系和數量關系等探究能力，下面幾個變式問題就是以這道題為“原題”的變式題。

【母題】在△ABC中，∠ACB=90°，AC=BC，直線MN經過點C，且AD⊥MN于D，BE⊥MN于E。

當直線MN繞點C旋轉到圖1的位置時，求證：△ADC≌△CEB；

證明（如圖）∵直線MN經過點C，∠ACB=90°，∴∠ACD+∠BCE=90°，

又AD⊥MN，∴∠ACD+∠DAC=90°，∴∠DAC=∠BCE。

∵BE⊥MN，∴∠ADC=∠CEB=90°，

在△ADC和△CEB中，∠DAC=∠BCE，AC=BC，∠ADC=∠CEB，

∴△ADC≌△CEB△ADC（AAS）。

【變式一】當直線MN繞點C旋轉到圖1的位置時，試猜想線段DE、AD、BE有怎樣的等量關系？請寫出這個等量關系，并加以證明。

DE=AD+BE。

理由：△ADC≌△CEB∴CD=BE，AD=CE，

∴AD=CE=CD+DE=BE+DE。

【變式二】當直線MN繞點C旋轉到圖2的位置時，試猜想線段DE、AD、BE有怎樣的等量關系？請寫出這個等量關系，并加以證明。

DE=AD-BE。

理由：∵△ADC≌△CEB∴CD=BE，AD=CE，

∵DE=CE-CD∴DE=AD-BE。

【變式三】當直線MN繞點C旋轉到圖3的位置時，試猜想線段DE、AD、BE具有怎樣的等量關系？請寫出這個等量關系，并加以證明。

DE=BE-AD。

理由：∵△ADC≌△CEB∴CD=BE，AD=CE，

∵DE=CD-CE∴DE=BE-AD。

一題多變，不僅可以培養學生的發散思維能力及相關知識點遷移能力，還可以大大擴大學生的知識容量，經常做這種訓練，不僅可以提高學生思維質量，還可以培養學生面對難題的良好的從容心態。

新課程標準中提倡“通過解決問題的反思，獲得解決問題的經驗”。數學教學離不開例題習題，而教學中如何選擇例題習題，從而挖掘教材潛在的智能價值，充分展示教學功能，并使課本知識有效地濃縮。通過不同角度、不同層次、不同情形、不同背景的變式，使一題多變，從而揭示不同知識點的聯系，使學生加深知識的理解與內化，使知識系統化，克服某些思維定勢，發散學生思維，培養學生思維的靈活性、全面性和創新性，提高學生解決實際問題和應變的能力。