基于改進粒子群算法的風電并網的無功優化研究

易繼澤，傅曉錦，陳建全

（上海電機學院，上海 200120）

0 引言

風能作為可持續、綠色的新能源被大幅度用于風力發電，但由于風的不確定性、不穩定性，使得風電系統的輸出功率具有波動性[1]，因此當風電接入電網時，風電并網系統會對電網系統產生較大幅度的電壓波動和閃變，同時，風電場裝置中的電子器件也易發生諧振現象，容易發生風電的運行事故[2]。因此接入的風電會影響整個電力系統的電能質量以及安全穩定的運行，若不采取相應措施來解決這些問題，將會造成巨大經濟損失，尤其是解決風電并網對電網穩定性影響的問題。目前，風電場并網的研究主要集中在風電場的低壓穿越能力、風功率預測和風電場的無功裝置安裝的位置以及無功功率補償上[3]。本文首先對風電并網帶來負面影響、系統無功優化的數學模型、粒子群算法等各個方面進行了闡述與研究，其次指出了存在的問題和改進方法以及基于改善后粒子群算法的風電并網系統無功優化方案，最后通過MATLAB在IEEE 9節點風電系統中仿真驗證了改進算法的有效性及實用性。

1 風電并網系統對于區域電網的主要影響

風電并網過程會對電網產生沖擊，風機在連網之前處于空轉狀態，在啟動、斷開瞬間將會產生巨大的沖擊電流（該值為電力系統額定電流的5～6倍）。當風力發電機系統與電網相連時，電網具備的感應負載特性使得電網絡相當于一個巨大的電抗器，導致瞬時變化的電流將形成巨大的沖擊電流，進而沖擊區域電網，降低區域電網的穩定性，同時會導致網絡損耗，從而使得電網運行效率變低[4-6]。

由于風速的不確定性的變化，風力發電機可能會導致無功功率的吸收。而且，由于風機的尾流效應、湍流和風速變化迅速將會引起的湍流會引起風功率的波動和風力機的頻繁啟停，最終這將影響系統正常運行[7-8]。風電的不穩定性勢必引起電網電壓變化，其主要表現為周期性的電壓波動、電壓驟降、電壓閃變及電氣設備損壞等[9]。

風電并網會影響區域電網的運行成本，由于風能不能有效控制，會嚴重破壞電網的有功功率平衡。為了保證風電并網后供電的可靠性，需要增加熱備功率，以避免因輸出變化而引起的有功功率短缺，從而實現電力系統的有功功率平衡。這是因為有功不足不僅會影響系統的有功功率平衡，而且基于工頻靜態特性對系統無功功率損耗有影響，改變無功電壓平衡[10-13]。

2 無功優化的作用與數學模型

2.1 無功優化的作用

基于無功優化，對電網運行進行改進[14-15]：① 降低電網崩潰甚至停電的事故率，提高電網的電能質量以及運行安全性；② 將電網相關點的電壓控制在標準范圍內，確保電網發電機所發電量能夠滿足供電需求；③ 合理分配和減少電網的無功損耗，減少無功功率設備的使用，減少變壓器、線路的負荷；④ 通過節能裝置減少電能的損耗繼而降低有功損耗，實現電網更加經濟性運行；⑤ 通過合理安排無功補償容量和位置，減少無功裝置與無功電源的建設投資。因此，合理穩定電力系統的電壓、優化系統無功功率以及提高電網電能質量是維持系統安全穩定運行的重要前提。

2.2 無功優化數學模型

無功優化問題是電力系統中較為復雜的非線性、多變量、多約束的一個規劃問題,變量通常是離散變量和連續變量，這兩種變量既有相互聯系又有制約，約束條件中包括等式和不等式約束[16]。必須要保證無功補償裝置輸入容量、變壓器分接頭的調節以及發電機端電壓的協調合適等條件。而且收斂依賴于初始值以及變量的數量，這是一個非常復雜的問題。

無功優化常用的數學模型包括目標函數和約束條件兩部分[17]。優化模型的通常數學模型為：

式中，u為控制變量；x為狀態變量；f(u，x)為電力系統無功優化目標函數；g(u，x)為等式潮流約束條件；h(u，x)為不等式變量約束條件。

若在系統狀態變量超出可行范圍時，需對目標函數增添罰值：

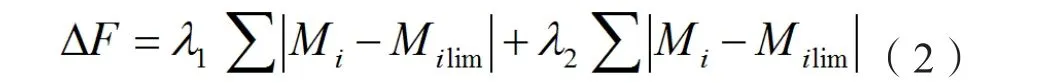
式中，λ1、λ2為罰值常數，Mi為系統狀態變量，Milim為狀態變量限制值。

最后的目標函數為原始目標函數與罰值之和：

式中，F1為原始目標函數，ΔF 為罰值函數。

3 基本粒子群算法

3.1 算法理論

算法的基本原理是[18]：隨機生成一定規模大小的初始粒子群。這些粒子在解空間中移動，且具有它們自己的當前位置和瞬時速度，粒子的維數等于控制變量的數目。粒子的位置是優化問題的可能解，并且速度對應于迭代期間產生的偏差量。將已知粒子位置值代入到適應值求解方程，得到當前位置處的粒子函數值，并用于評估粒子的質量。通過對所有最佳位置點的分析和比較，選擇最佳的位置點。但是一般粒子將圍繞該最佳點移動并通過連續迭代搜索獲得全局最優解。在每次迭代中，每個粒子由遵循兩個最優解的規則來確定其速度和位置：一個是單個粒子經歷的最優位置，即單個最優解；另一個是當前的最優位置由粒子群總體找到的，則這個最優位置為全局最優解[19]。

若已知某粒子群個體總數為N，且每個粒子的搜索的空間維度為D維[20]，則：第i個粒子在該空間中，位置矢量為：xi=A（xi1,xi2,…xid,…,xiD）；速度矢量表示為：vi=（vi1,vi2,…vid,…,viD）；粒子當前的所有經歷最優位置Pbest表示為：Pi=（Pi1,Pi2,…Pid,…,PiD；群體的全局最優位置解gbest為：Pg=（Pg1,Pg2,…Pgd,…,PgD）；在每次的循環中，每個粒子要調整自己的速度和位置將要用式（4）代入求解：

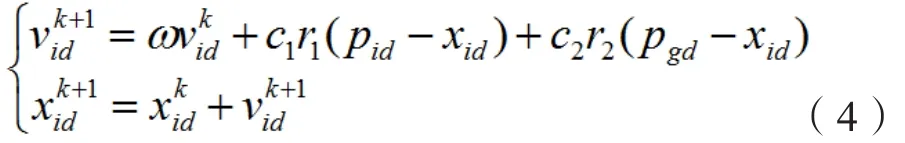
其中，ω為慣性權重，k為循環總數，c1、c2為學習因子，r1、r2為[0,1]范圍內的隨機值。

PSO算法對速度的約束條件[20]：

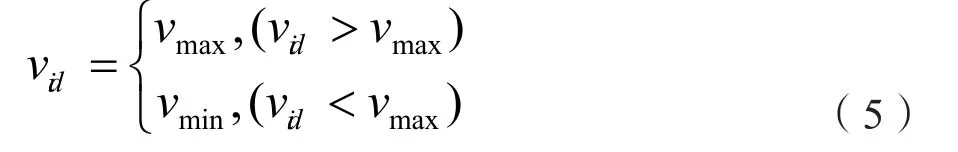
其中，vmax是粒子移動快慢的上限，vmin是粒子移動快慢的下限，為提高粒子的搜索精度，避免搜索到局部最優而無法跳出，必須合理選擇vmax值。

3.2 粒子群算法改進的方案

上文所介紹的粒子群算法為未改進的算法，在標準粒子群算法中，根據粒子的收斂特性，粒子的收斂是以飛行軌跡的形式實現的。由于粒子速度的限制而使搜索的范圍不能擴展到整個可行解空間，也因此導致了搜索空間的每個迭代步驟的有限區域。PSO算法由于其收斂性較為發散，因此最大的缺點弊端是不能保證完全搜索到全局最優解。可以通過改善PSO的收斂性來改進PSO算法，本文中采取非線性慣性權重的方法，則更新慣性權重ω和粒子速度v公式為

式中：ωa，ωb分別為慣性權重初始值與最后值，Mamax為粒子進行迭代時的最大迭代次數；pti為第t次迭代的個體極值；ptg為第t次迭代的群體極值，a1和a2為兩個加速常數。

3.3 改進后PSO算法的原理流程圖

改善后PSO算法原理流程圖如圖1所示：

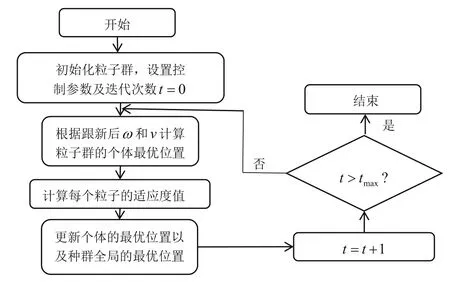
圖1 改善后PSO算法原理流程Fig.1 Improving the principle flow of PSO algorithm

4 改進后的粒子群算法在風電并網系統的無功優化中的應用

隨著接入電網的風電容量逐漸增加，風電系統會導致電網電能質量下降，在嚴重的情況下，甚至會導致電網系統崩潰和停電。因此，本文采用改進后的粒子群算法，通過對變壓器分接頭的位置、風機端電壓的大小和無功補償容量以及無功裝置的位置作為控制變量進行優化設置，達到穩定風電并網系統中的電壓以及補償系統無功功率來改善電網的電能質量和安全穩定運行。

以風電并網系統的網絡損耗最小作為目標函數，則其表達式為

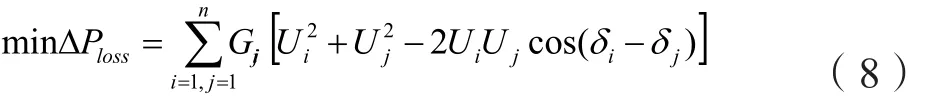
式中：i、j為節點編號；n為并網系統的節點總數；Gij為支路電導；Ui、Ui為節點i、j電壓的幅值；δi、δj為節點i、j電壓的相角。

以系統的潮流方程為等式約束條件：

對于 PV 節點，還需增加約束方程：

最終優化結果的可行范圍還需滿足電壓和無功安全性約束等條件：

在系統電壓超出可行范圍時，則有式 有：

最后風電并網系統的目標函數為有功功率損耗與罰值之和：

5 算例分析

為了驗證改進粒子群算法的有效性和實用性，在MATLAB中對IEEE 9風電系統進行了仿真，并對改進算法前后進行無功優化后的有功損耗和節點電壓進行了分析和比較。IEEE 9節點系統的拓撲結構如圖2所示。有三個電源，九個節點和九個分支，三個分別連接到節點1, 2和3，將風力發電機分別接于節點 4、7、9，相關參數如表 1：

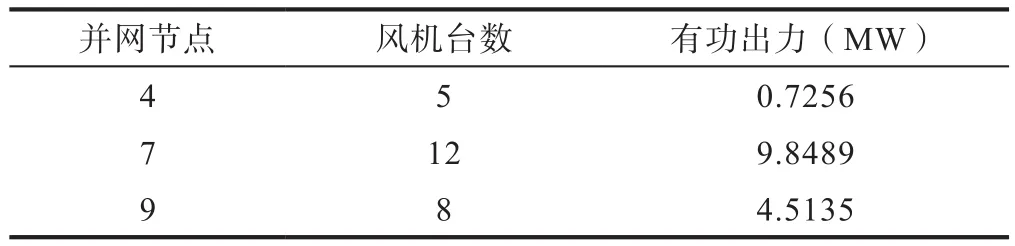
表1 不同數量的風機并網參數Table 1 Fan connected parameters

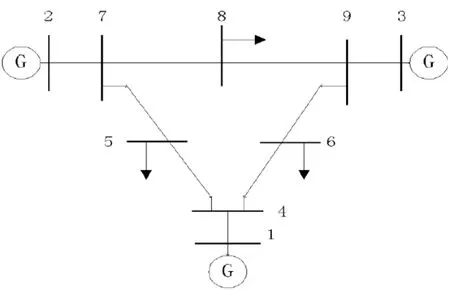
圖2 IEEE 9節點風電系統拓撲圖Fig.2 IEEE 9 node system topology

5.1 仿真結果

將原有粒子群算法應用于風電系統無功優化后的結果作為對照組與改進后的粒子群算法的仿真結果進行了比較。圖3和4是改進前后粒子群優化算法的迭代收斂曲線。在表2中記錄改善PSO前后優化后的結果。

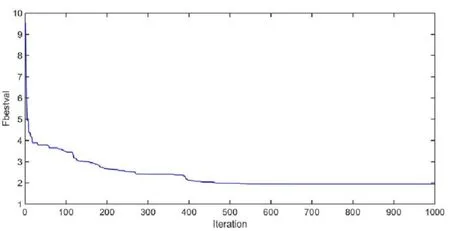
圖3 改善前粒子群算法的迭代收斂曲線Fig.3 Improving iterative convergence curve of PSO algorithm

圖4 改善后PSO優化算法迭代收斂曲線Fig.4 Iterative convergence curve of improved PSO optimization algorithm

在PSO改進前后優化后，分別記錄有功損耗和主要控制變量，包括各發電機的無功輸出、各發電機端的電壓以及并聯電容器的安裝容量。相關數值如表2所示。

表2 改善PSO前后進行無功優化的結果對比Table 2 Simulation results of PSO optimization after node system improvement

針對PSO優化前的控制變量參數而言，改善PSO后無功優化系統中的因變量節點的電壓也得到了優化。比較風電連入電網前后的節點電壓以及改進前后PSO算法優化后的節點電壓，繪制了上述對比的節點間電壓表3和電壓對比曲線圖5，并進行對比分析。

根據以上數據，繪制成曲線圖如圖5所示。

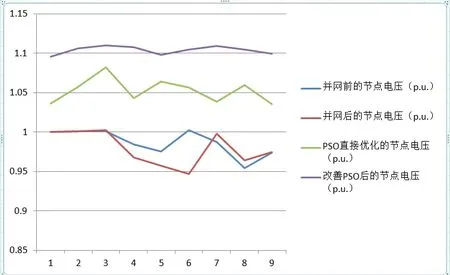
圖5 改進前后PSO算法所得系統節點電壓曲線圖Fig.5 The PSO algorithm is used to optimize the voltage curve of the node before and after improvement

5.2 數據處理

由公式有：

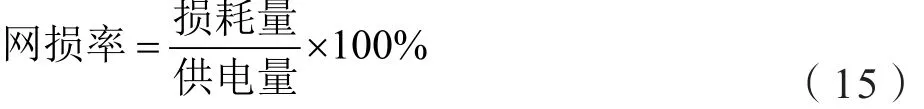
則在IEEE9節點風電并網系統中，根據潮流分析計算出接入風能后用改進PSO前后進行優化電力系統發電機的有功出力，最終算得各數據對比變化如表4：

表4 PSO進行優化前后各數據對比Table 4 Comparison of data before and after PSO optimization

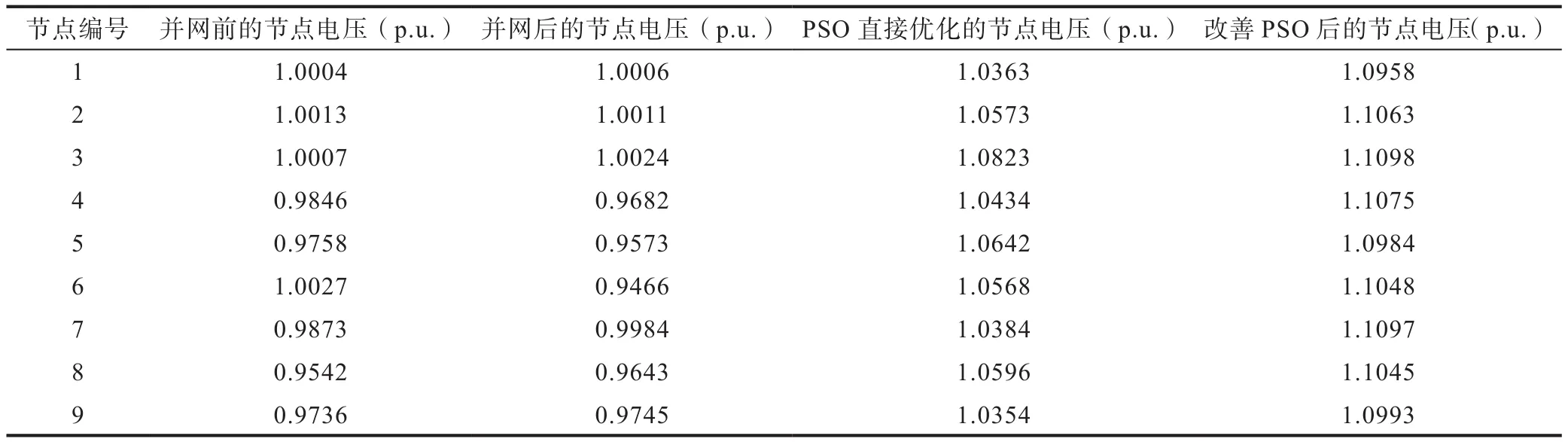
表3 9個電壓節點風電系統的節點電壓表Table 3 Node voltage meter of IEEE9 node system

5.3 結果分析

通過對比改善前后PSO進行無功優化后的網損值，可以得出這樣的結論：經過改善PSO算法后再優化，風電并網系統的總有功損耗從5.2776MW下降至4.3658MW，下降了17.8474%，同時，網損率由改善PSO前的1.7278%下降了至1.3178%，降低了14.3046%。此外，圖4中列圖的趨勢表明，系統節點電壓比改進PSO之前的節點電壓更穩定，并且改進算法后節點電壓電平有效地增加，并且電壓分布顯著改善。以上結果還表明，本文提出的改進算法可以進一步降低系統損耗，而且能更有效地減小電壓偏移，達到更好的優化效果。

6 結論

本文建立了風電并網系統的無功優化數學模型，并利用改進的粒子群優化算法對IEEE 9節點系統進行仿真和優化。結果表明改進算法具有較好的收斂性，通過比較改進前后算法的優化數據，發現優化后的網絡損耗進一步降低，電壓分布顯著改善，從而改善了電力系統的電能質量以及達到電網穩定運行的條件，驗證了改進的粒子群優化算法的有效性和實用性。