塔式光熱電站儲熱系統容量優化配置

毛維宙 陸華軍 單寶奇

?

塔式光熱電站儲熱系統容量優化配置

毛維宙1陸華軍1單寶奇2

（1. 南京磐能電力科技股份有限公司，南京 210061；2. 河海大學能源與電氣學院，南京 210098）

儲熱系統是塔式光熱電站的重要組成部件，其容量大小一般用儲熱時間來描述。儲熱時間是儲熱系統所能儲存的熱量可以供汽輪發電機組在額定工況下運行的最大時間。目前已建的塔式光熱電站的儲熱時間取值比較隨意，未考慮其對電站經濟效益的影響，本文提出了一種考慮綜合經濟效益對電站儲熱時間進行優化的方法，以在我國西部某地區建設50MW塔式光熱電站為例，使用該地區的實際地理氣象數據,建立了塔式光熱電站的能量轉換效率模型及經濟性評價模型，以平準化度電成本最低為優化目標，分別得到了太陽倍數分別為1.8和2.4時電站的最優儲熱時間取值，分析了在一定太陽倍數下，儲熱系統容量對電站經濟效益的影響，并分析了儲熱系統容量對電站年容量因子的影響。

塔式光熱電站；儲熱系統；儲熱時間；平準化度電成本

目前，光熱電站的形式主要包括槽式、塔式、線性菲涅爾式和碟式四種[1]。其中，塔式光熱發電的聚光比較高，太陽能轉化率高，發電效率提升空間更大，因此是最具有開發潛力的光熱發電形式，也是大規模太陽能發電的最理想方式[2]。

目前國內外對于塔式光熱電站儲熱系統的研究主要集中在儲熱系統結構設計、儲熱系統仿真等方面，而對儲熱系統容量優化的研究較少。文獻[3]分析了目前儲熱系統的發展概況，比較了油鹽和熔鹽作為太陽能熱電站的儲熱介質的經濟性，得到了用來判斷兩者經濟性優劣的比例曲線，并以50MW容量的太陽能熱電站為例，建立了儲熱系統的經濟性評價模型，通過模擬計算分析，對50MW電站的儲熱系統進行了優化設計，最終得出了儲熱系統的最佳結構。文獻[4]介紹了儲熱系統設計方法的概況以及太陽能熱電站儲熱系統設計時在不同層次上需要考慮的因素，討論了儲熱系統設計以及應用到太陽能熱電站中的各種儲熱系統的熱能和效率分析。文獻[5]開發了一種新的溫躍層儲熱罐仿真模型，解決了以往文獻中模型的不足，并將新的模型并入了一個100MW塔式太陽能熱發電系統模型中，研究了溫躍層儲熱罐長期運行期間的儲熱性能。

本文在建立塔式光熱電站的能量轉換效率模型及經濟性評價模型的基礎上，以平準化度電成本最低為優化目標，分別得到了太陽倍數分別為1.8和2.4時電站的最優儲熱時間取值。

1 塔式光熱電站能量轉換效率分析

1.1 塔式光熱電站的組成及原理

通常，塔式光熱電站主要由以下3個子系統組成：①聚光集熱子系統，其作用是收集匯聚太陽能并將太陽能轉化為傳熱介質的熱能；②儲熱子系統，其作用是儲存熱能，供太陽能不足時發電使用；③熱力發電子系統，其作用是將熱能轉化為電能，與常規發電相似。

塔式光熱發電原理如下：利用大量獨立跟蹤太陽的定日鏡，將太陽光線聚焦到一個固定在高塔頂端的吸熱器上，加熱其中的工質（熔融鹽）產生高溫介質，高溫介質加熱水產生過熱蒸汽，帶動汽輪機、發電機旋轉發電[6]。塔式光熱電站的實物圖如圖1所示。

圖1 塔式光熱電站實物圖

下文通過分析各子系統的能量轉換效率，建立塔式光熱電站的能量轉換效率模型。

1.2 定日鏡場光學效率模型

1）定日鏡效率組成

定日鏡在工作時會受很多因素的影響，產生多種光學損失，使定日鏡反射到吸熱器的能量小于定日鏡理論上能夠接收的太陽能。定日鏡場的這一特性可以用其光學效率來表達。定日鏡場的總光學效率由單臺定日鏡光學效率綜合得來，根據光學效率的影響因素，單臺定日鏡的光學效率包括余弦效率，大氣透射效率，鏡面反射效率，陰影和阻擋效率等。

若單臺定日鏡的面積為，則第臺定日鏡反射到吸熱器入口處的能量P為式（1）。

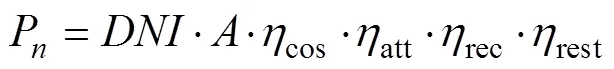
2）余弦效率計算

為使反射光線到達接收器，定日鏡工作時，其表面不能總與太陽入射光保持垂直，而是呈現一個傾斜角。余弦損失就是因這種傾斜所導致的定日鏡反射面面積相對于太陽光可見面積的減少而產生 的[7]。余弦效率可通過式（2）計算。

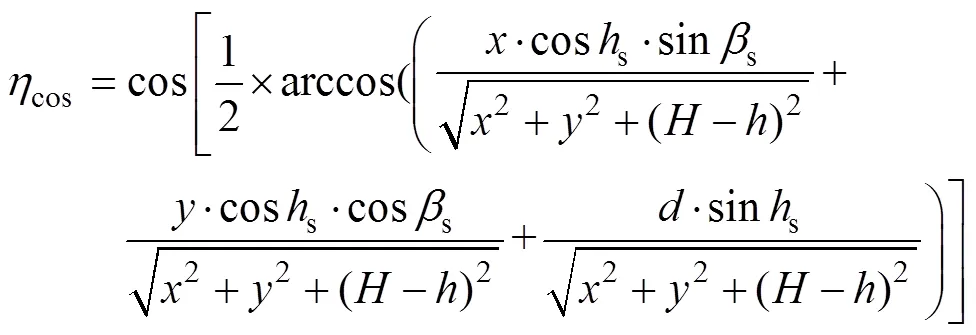
3）大氣透射效率計算

定日鏡場中任意一面定日鏡的大氣透射效率可通過式（3）[8]計算。

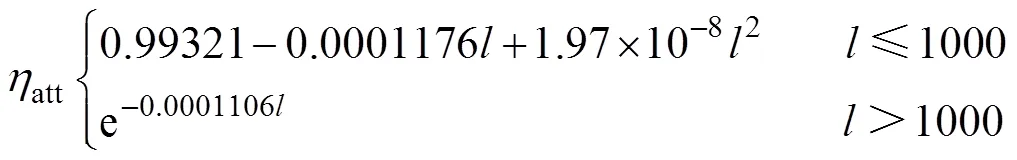
式中，為定日鏡場中任意一面定日鏡的鏡面中心到吸熱器中心的距離，m。

1.3 吸熱器能量轉換效率模型

1）吸熱器的熱損

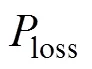
2）吸熱器的反射熱損

3）吸熱器的輻射熱損

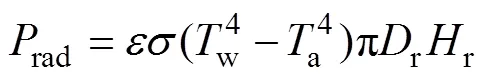
4）吸熱器的對流熱損

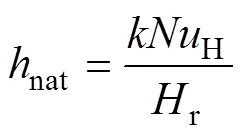
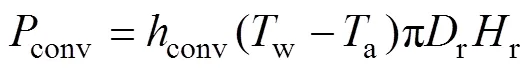
5）吸熱器的熱效率

由上可知，得到利用的有效熱能，即

1.4 儲熱系統能量轉換效率模型

1）充熱效率

儲熱系統的充熱效率定義為

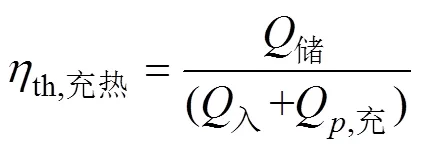
式（12）描述了從儲存在高溫熔鹽罐中的熱量相對于輸入高溫熔鹽罐的熱量和泵送能量的比。

2）放熱效率

放熱效率定義為

式（13）描述了從高溫熔鹽罐提取的熱量相對于儲存的能量和抽取所需的泵送能量的比。

3）整體效率

儲熱系統的整體熱效率定義為

式（14）描述了用于單個充/放熱循環的回收熱量與輸入熱量和泵送能量的比。

1.5 熱力發電系統能量轉換效率模型

來自定日鏡場或儲熱系統的能量進入熱力發電系統轉化為電能，這個過程的整體效率與負載水平呈非線性關系[11]。

文獻[11]中的圖3表示了熱力發電系統效率與負載水平的函數關系，對其進行變換可得50MW塔式光熱電站熱力發電系統的整體效率與輸入熱量的函數關系，如圖2所示。

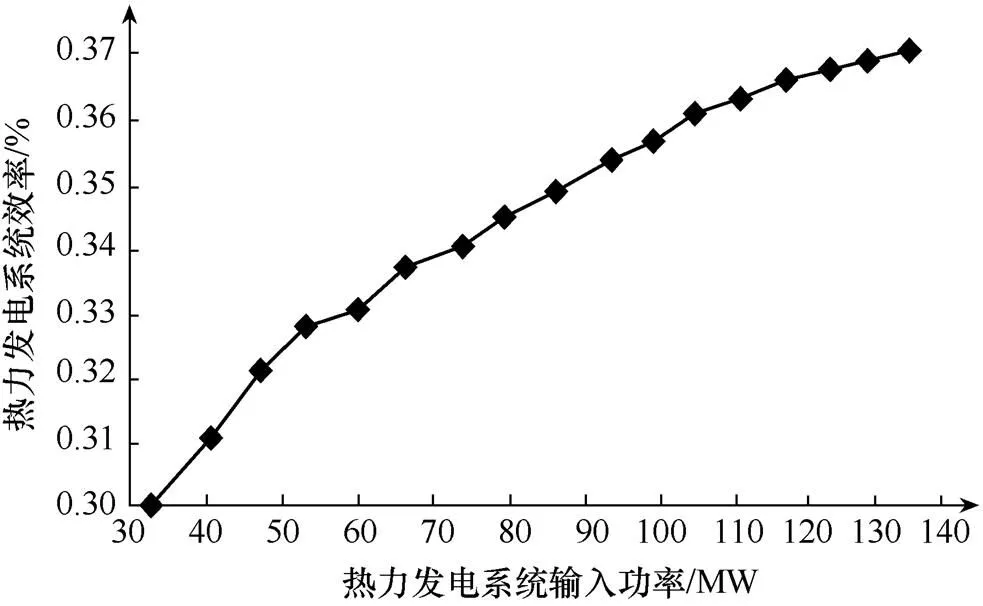
圖2 50MW塔式光熱電站熱力發電系統整體效率與輸入熱量關系圖

2 塔式光熱電站儲熱系統容量優化目標

2.1 太陽倍數和儲熱時間

太陽倍數和儲熱時間是影響塔式光熱電站經濟性評價的兩個關鍵參數[12]。電站容量確定以后，太陽倍數和儲熱時間分別是鏡場容量和儲熱系統容量的直接反映。因此，本文在對儲熱系統容量進行優化配置時，選擇固定太陽倍數，調節儲熱時間，觀察其對電站LCOE的影響，并以LCOE最低時的儲熱時間作為最優取值。

塔式光熱電站儲熱系統的容量一般用儲熱時間來描述。儲熱時間是儲熱系統所能儲存的最大熱量可以供汽輪發電機組在額定工況下運行的時間。

2.2 平準化度電成本（LCOE）

LCOE是指當電站整個壽命周期內的總收益與總成本相等時的上網電價，也可理解為電站壽命周期內每發1kW·h電所需投資的成本。當電價高于此值時將產生更大的資本回報率，而低于此值時將會降低資本回報率甚至虧損。

LCOE是充分考慮了一座光熱電站整個壽命周期內的投資，以及運行、維護、管理成本的一個綜合性的參數，可根據式（15）計算[13]

塔式光熱電站的成本計算數據[14-15]見表1。

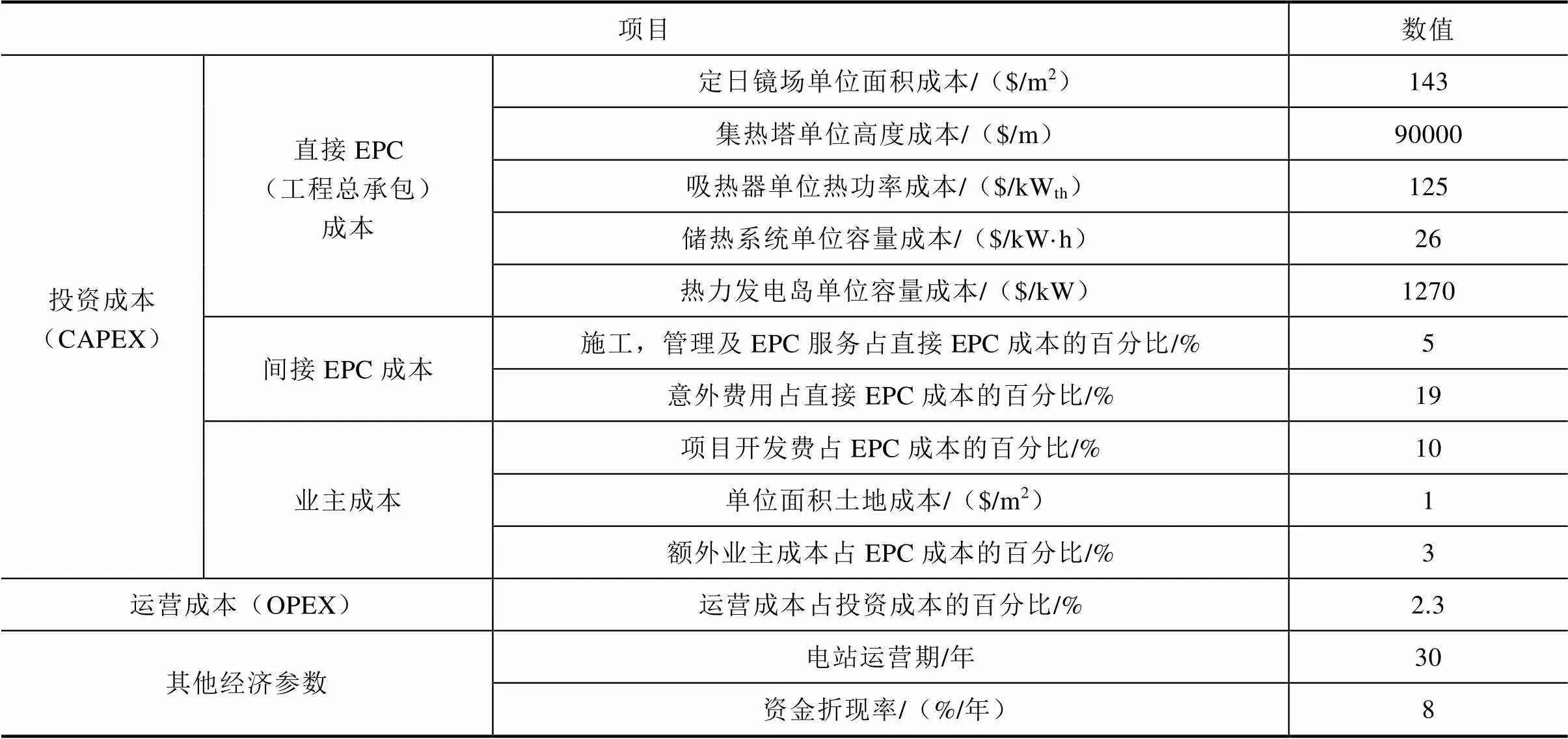
表1 塔式光熱電站成本計算數據

本文年發電量計算采用基于逐時模擬的年發電量計算方法。該方法的要點是，根據一年內逐時的太陽輻照度數據，通過基于系統能量平衡的模擬來計算不同聚光場面積下的集熱場輸出與汽輪機額定輸入之間的關系，以得到該汽輪機容量下的年最大發電量。

2.3 年容量因子

年容量因子是考慮光熱電站年發電小時數的重要數據，也是電站年運行性能的反映。它是指電站實際年發電量與電站滿負荷運行一年所發電量之比，可按照式（16）計算[16]。

3 模型驗證

3.1 設計點參數選取

本文以在我國西部某地區建設50MW熔鹽塔式光熱電站為例建模，使用該地區的實際地理氣象數據，并選擇春分日正午12∶00的氣象數據作為電站設計點參數，見表2。

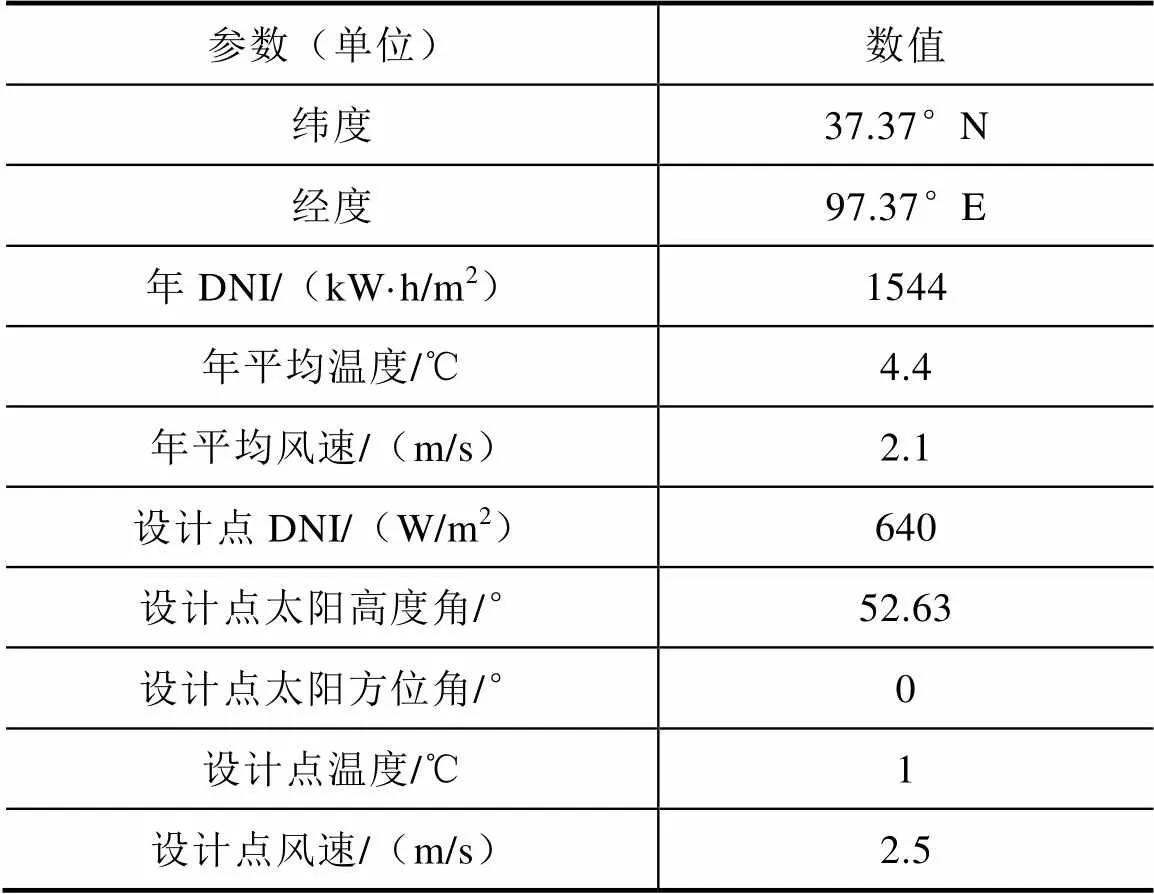
表2 我國西部某地區年地理氣象數據及設計點參數表

3.2 儲熱系統容量優化配置

在以上設計點參數下，分別分析太陽倍數取1.8和2.4兩種情況，儲熱時間分別取0～16h，間隔取2h，分析各個儲熱時間取值下電站LCOE的變化情況，得到電站綜合經濟效益隨儲熱時間的變化規律，以最低LCOE為目標得到兩種情況下儲熱時間的最佳取值。通過分析年容量因子的變化規律，得到儲熱時間對電站運行性能的影響。

1）LCOE分析

當太陽倍數分別被取1.8和2.4時，電站在各個儲熱時間取值下的LCOE分布分別如圖3和圖4所示。

由圖3可以看出，當太陽倍數取1.8時，LCOE隨儲熱時間先下降后上升，在儲熱時間取6h時，LCOE最低，為0.2113$/kW·h。這是由于，當儲熱時間小于6h時，定日鏡場采集的太陽輻射能并未完全利用起來，定日鏡場容量仍有一定裕量，此時如果增加儲熱時間，就能將定日鏡場采集的多余太陽輻射能儲存起來，供太陽輻射不足時發電使用，從而電站發電量能夠隨儲熱時間的增大而顯著增加，因此LCOE會下降。當儲熱時間大于6h時，定日鏡場采集的多余太陽輻射能已基本可以被儲熱系統全部吸收，此時即使繼續增加儲熱時間，由于定日鏡場能夠采集的太陽能有限，電站的年發電量隨儲熱時間的增加速率已十分緩慢，而電站投資仍然會隨著儲熱時間的增加而大大增加，因此LCOE會隨儲熱時間的增加而上升。

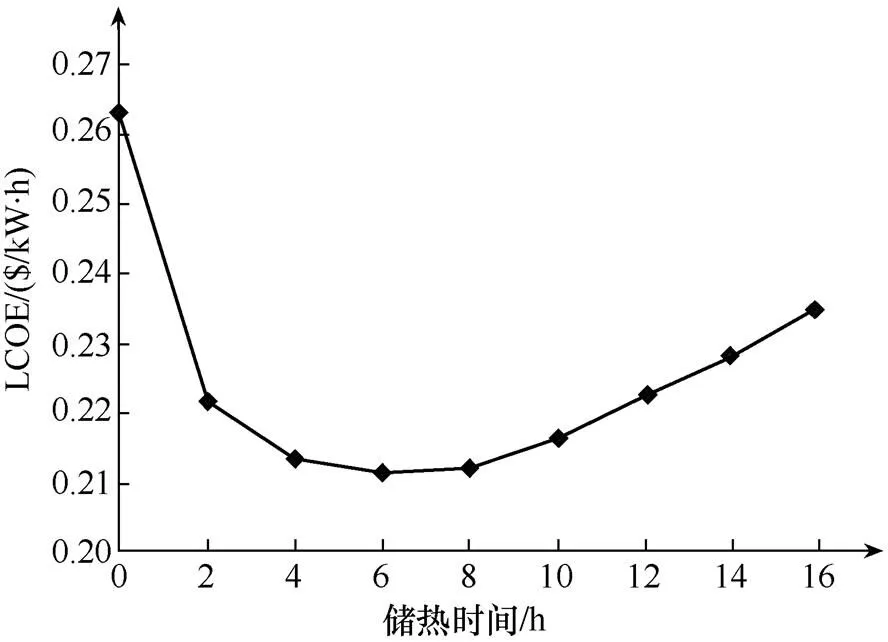
圖3 太陽倍數為1.8時的LCOE分布圖

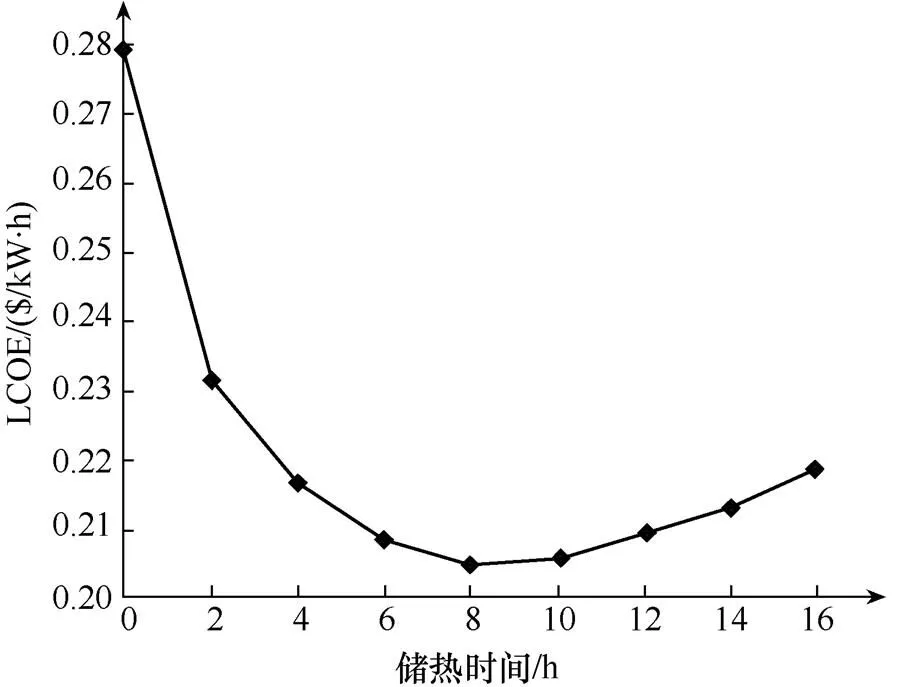
圖4 太陽倍數為2.4時的LCOE分布圖

當太陽倍數取2.4時，LCOE隨儲熱時間的變化規律與太陽倍數取1.8時類似，在儲熱時間取8h時，LCOE最低，為0.2049$/kW·h，如圖4所示。

以上分析說明，太陽倍數為1.8時，儲熱時間取6h時電站的綜合經濟效益最優；太陽倍數為2.4時，儲熱時間取8h時電站的綜合經濟效益最優。

2）電站年容量因子分析

太陽倍數分別取1.8和2.4時，電站在各個儲熱時間取值下的年容量因子分布分別如圖5和圖6 所示。

由圖5可以看出，隨著儲熱時間從0～16h，電站的年容量因子從27.83%～39.74%。這是因為，儲熱時間越長，儲熱系統容量越大，儲熱系統能夠儲存的多余太陽輻射能越多，在太陽輻射不足時能夠供給熱力發電系統的熱量越多，從而使發電時間增長，發電量增加，年容量因子增大。但是，由于太陽倍數已固定為1.8，定日鏡場能夠采集的太陽輻射能有限，當儲熱系統的容量已經足以將定日鏡場采集的多余的太陽輻射能全部儲存時，若繼續增加儲熱時間，則增加的儲熱容量會被浪費，發電量不再增長，因此，年容量因子隨儲熱時間的增長趨勢不會一直持續，而是逐漸減緩，最終趨于一個最大值。

圖5 太陽倍數為1.8時的年容量因子分布圖

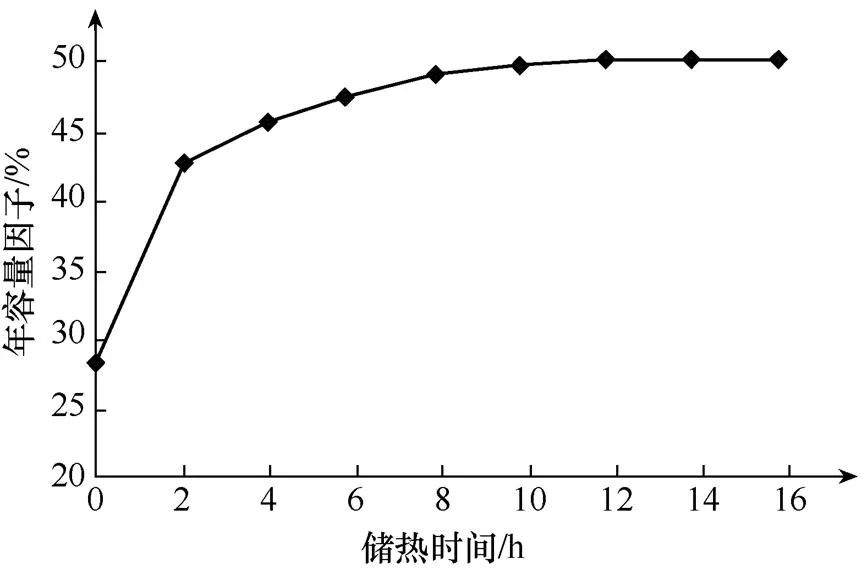
圖6 太陽倍數為2.4時的年容量因子分布圖

當太陽倍數取2.4時，年容量因子隨儲熱時間的變化規律與太陽倍數取1.8時類似，如圖6所示。

根據以上分析，年容量因子隨儲熱時間的增加而增大。因此，增加儲熱時間有利于提高電站年發電量，提高電站的運行性能。但是，儲熱時間并不是可以無限制的增加，當儲熱系統足夠將定日鏡場采集的多余太陽輻射能儲存時，繼續增加儲熱時間反而會造成投資浪費。

4 結論

本文以在我國西部某地區建設50MW塔式光熱電站為例，建立了電站的能量轉換效率模型和經濟性評價模型，研究了定太陽倍數下儲熱系統容量對電站運行性能及綜合經濟效益的影響，得到以下結論。

1）太陽倍數一定時，電站LCOE隨太陽倍數的增大先下降后上升。

2）太陽倍數為1.8時，當儲熱時間取6h時電站的LCOE最低，經濟效益最好。

3）太陽倍數為2.4時，當儲熱時間取8h時電站的LCOE最低，經濟效益最好。

4）太陽倍數一定時，年容量因子隨儲熱時間的增加而增大，但增長趨勢會逐漸減緩，最終趨于一個最大值。

[1] 上海市建材科技情報研究所. 太陽能光熱發電技術的發展[J]. 上海建材, 2017(1): 16-18.

[2] 彭玲玲. 走進太陽能發電新時代[J]. 中國科技獎勵, 2011(10): 66-67.

[3] 張雅文. 太陽能電站雙罐式熔鹽蓄熱系統的優化設計及研究[D]. 武漢: 華中科技大學, 2012.

[4] Kuravi S, Trahan J, Goswami D Y, et al. Thermal energy storage technologies and systems for con- centrating solar power plants[J]. Progress in Energy and Combustion Science, 2013, 39(4): 285-319.

[5] Flueckiger S M, Iverson B D, Garimella S V. System-level simulation of a solar power tower plant with thermocline thermal energy storage[J]. Applied Energy, 2014, 113(SI): 86-96.

[6] 黎韋偲, 馬紀明. 塔式太陽能電站定日鏡場的聚焦策略研究[J]. 可再生能源, 2016, 34(4): 475-480.

[7] 潘磊, 李麗娟, 丁婷婷. 塔式太陽能熱發電鏡場中余弦效率仿真研究[J]. 可再生能源, 2013, 31(2): 1-5.

[8] 賈亞晴. 塔式太陽能光熱配套電站系統仿真研究[D].華北電力大學, 2015.

[9] Wu Shuangying, Xiao Lan, Cao Yiding, et al. Con- vection heat loss from cavity receiver in parabolic dish solar thermal power system: A review[J]. Solar Energy, 2010, 84(8): 1342-1355.

[10] Siebers D L, Kraabel J S. Estimating convective energy losses from solar central receivers[J]. Cavity Receivers, 1984.

[11] Usaola J. Operation of concentrating solar power plants with storage in spot electricity markets[J]. IET Renewable Power Generation, 2012, 6(1): 59-66.

[12] Jennie Jorgenson, Paul Denholm, Mark Mehos, et al. Estimating the performance and economic value of multiple concentrating solar power technologies in a production cost model[R]. Golden: National Rene- wable Energy Laboratory, 2013.

[13] Renewable energy technologies: cost analysis series[R]. International Renewable Energy Agency, 2012.

[14] Dieckmann S, Dersch J, Giuliano S, et al. LCOE reduction potential of parabolic trough and solar tower CSP technology until 2025[C]//Solarpaces Conference. AIP Publishing LLC, 2017.

[15] 李心, 趙曉輝, 李江燁, 等. 塔式太陽能熱發電全壽命周期成本電價分析[J]. 電力系統自動化, 2015, 39(7): 84-88.

[16] Izquierdo S, Monta?és C, Dopazo C, et al. Analysis of CSP plants for the definition of energy policies: The influence on electricity cost of solar multiples,capacity factors and energy storage[J]. Energy Policy, 2010, 38(10): 6215-6221.

Optimal allocation of thermal storage system capacity of solar power tower plant

Mao Weizhou1Lu Huajun1Shan Baoqi2

(1. Nanjing PANENG Technology Development Co., Ltd, Nanjing 210061;2. College of Energy and Electrica, Hohai University., Nanjing 210098)

Thermal storage system is an important component of solar power tower plant. Its capacity is generally described by thermal storage time. Thermal storage time is the maximum time that the thermal energy stored in the thermal storage system can be used for the operation of the steam turbine generator unit under rated condition. At present, the value of the thermal storage time of solar power tower plants that have been built is relatively arbitrary and its impact on the economic benefits of the power plant is not considered. This paper proposes a method for optimizing the thermal storage time of solar power tower plant considering the comprehensive economic benefits. We take the construction of 50MW solar power tower plant in a certain area of western China as an example. Using actual local geographic and meteorological data to establish the energy conversion efficiency model and economic evaluation model of solar power tower plant. The optimization objective is the minimum leveling cost of electricity. The optimal thermal storage time of the plant is obtained when the solar multiple is 1.8 and 2.4 respectively. And we analyzed the influence of the capacity of the thermal storage system on the economic benefit of the plant at certain solar multiple and the influence of thermal storage system capacity on annual capacity factor of power station.

solar power tower plant; thermal storage system; thermal storage time; leveling cost of electricity

2018-06-06

毛維宙（1990-），男，江蘇省鎮江市丹陽人，本科，助理工程師，主要從事繼電保護及配電設備營銷管理工作。