聚酰亞胺短纖維線密度與拉伸強度的概率分布分析*

1.湖南工程學院紡織服裝學院，湖南 湘潭 411104；2.湖南永霏特種防護用品有限公司，湖南 湘潭 411101；3.深圳微納先材科技有限公司，廣東 深圳 518035

聚酰亞胺為主鏈上含有酰亞胺環的一類聚合物，其具有良好的熱氧化穩定性、阻燃性能、高低溫性能、力學性能、耐輻射性能和絕緣性能，以及較好的化學穩定性[1]。因其綜合性能優良，眾多學者對其制備工藝[2-5]、結構與性能[6-10]等進行了較為深入的研究，但對纖維的線密度和強度方面的研究相對較少[11]。

因加工和使用過程中纖維內部和表面存在隨機分布的缺陷，導致纖維的拉伸強度表現出一定的隨機性和分散性。同時，紡絲過程中因原料性能和工藝參數的波動，將導致纖維的線密度也呈現一定的波動[12]。目前，在表征纖維線密度和拉伸強度時，通常采用多次測試結果的平均值，其建立于纖維線密度和拉伸強度的離散分布規律符合正態分布的假設。前期研究[11]發現，聚酰亞胺短纖維的線密度和拉伸性能指標均呈現偏態分布特征，因而采用平均值來評價纖維的線密度和拉伸性能指標值得討論。

基于此，為了深入研究聚酰亞胺短纖維的線密度和拉伸強度的分布特征，本文基于原位測量法對3種聚酰亞胺短纖維的線密度和拉伸強度進行了測試，并采用分布模型從統計學的角度對線密度和拉伸強度的離散程度進行了分析。

1 試驗對象及方法

1.1 試驗樣品

本文以甲綸(Suplon?)短纖維和P84短纖維(江蘇氟美斯環保節能新材料有限公司提供，工業級)以及軼綸(Yilun?)短纖維(深圳微納先材科技有限公司提供，民用級)為試驗對象。

1.2 纖維線密度

參考GB/T 16256—2008《紡織纖維 線密度試驗方法 振動儀法》，在XD-1型振動式纖維細度儀上測試纖維線密度。將試樣隨機分成50等份，每等份中隨機選取1根纖維進行測試，夾持隔距為20 mm，預加張力為0.35 cN。

1.3 纖維拉伸強度

參考GB/T 14337—2008《化學纖維 短纖維拉伸性能試驗方法》，采用XQ-1型纖維強度儀，對線密度測試后的纖維進行拉伸強度測試，以做到原位測量。為減少因張力夾更換而導致測量區域改變，盡可能做到線密度和拉伸強度的測試區域一致。纖維拉伸強度測試時，預加張力和夾持隔距與線密度測試時保持一致，均為0.35 cN和20 mm，加載速度為40 mm/min，有效測量樣品為50個。

所有測試均在標準大氣條件下進行，測試前試樣在標準大氣條件下平衡24 h。

2 試驗結果與分析

2.1 試驗結果

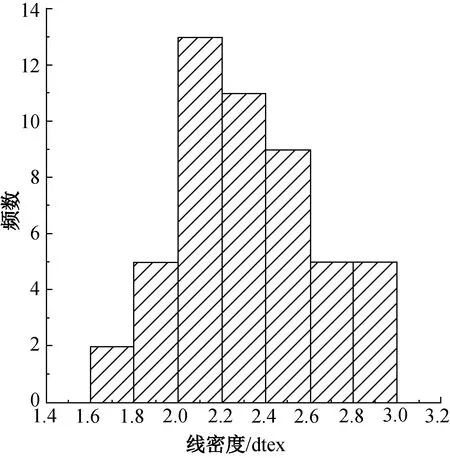
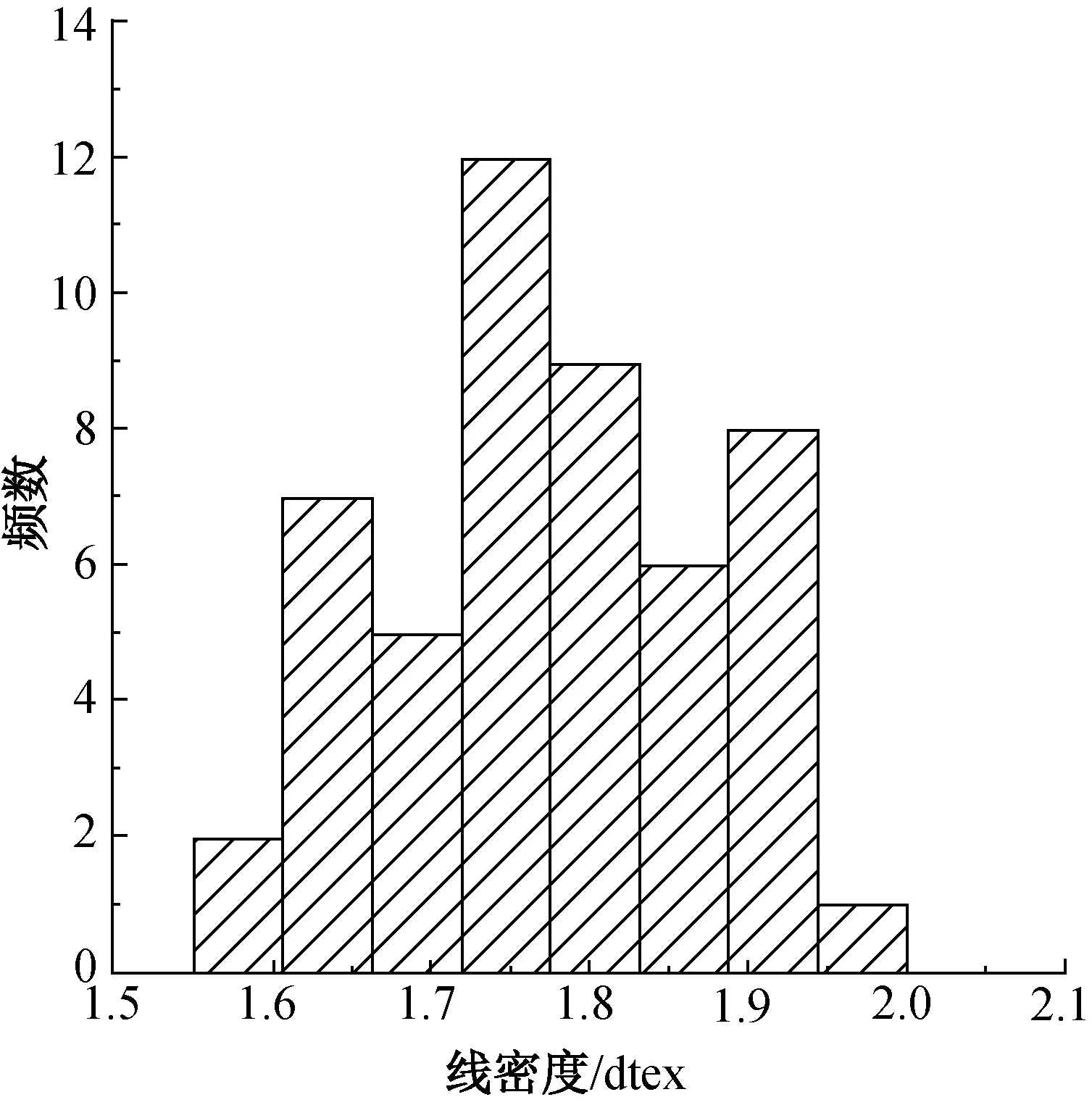
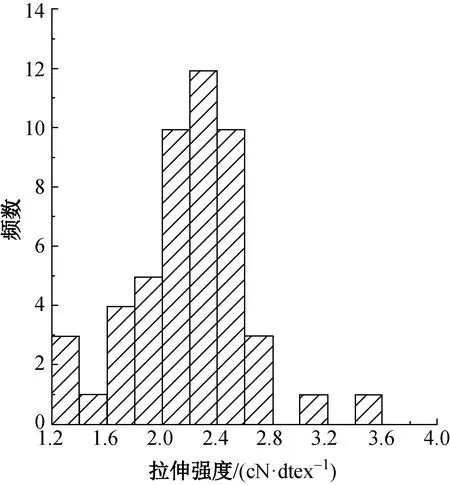
3種聚酰亞胺短纖維的線密度以及原位測量獲得的拉伸強度分布見圖1和圖2。由圖1和圖2可知，3種纖維的線密度與拉伸強度均呈現一定的離散性，且多數頻數不集中在中央位置，即呈現不對稱分布特征，因而采用正態分布來描述纖維的線密度和強度分布是值得討論的。

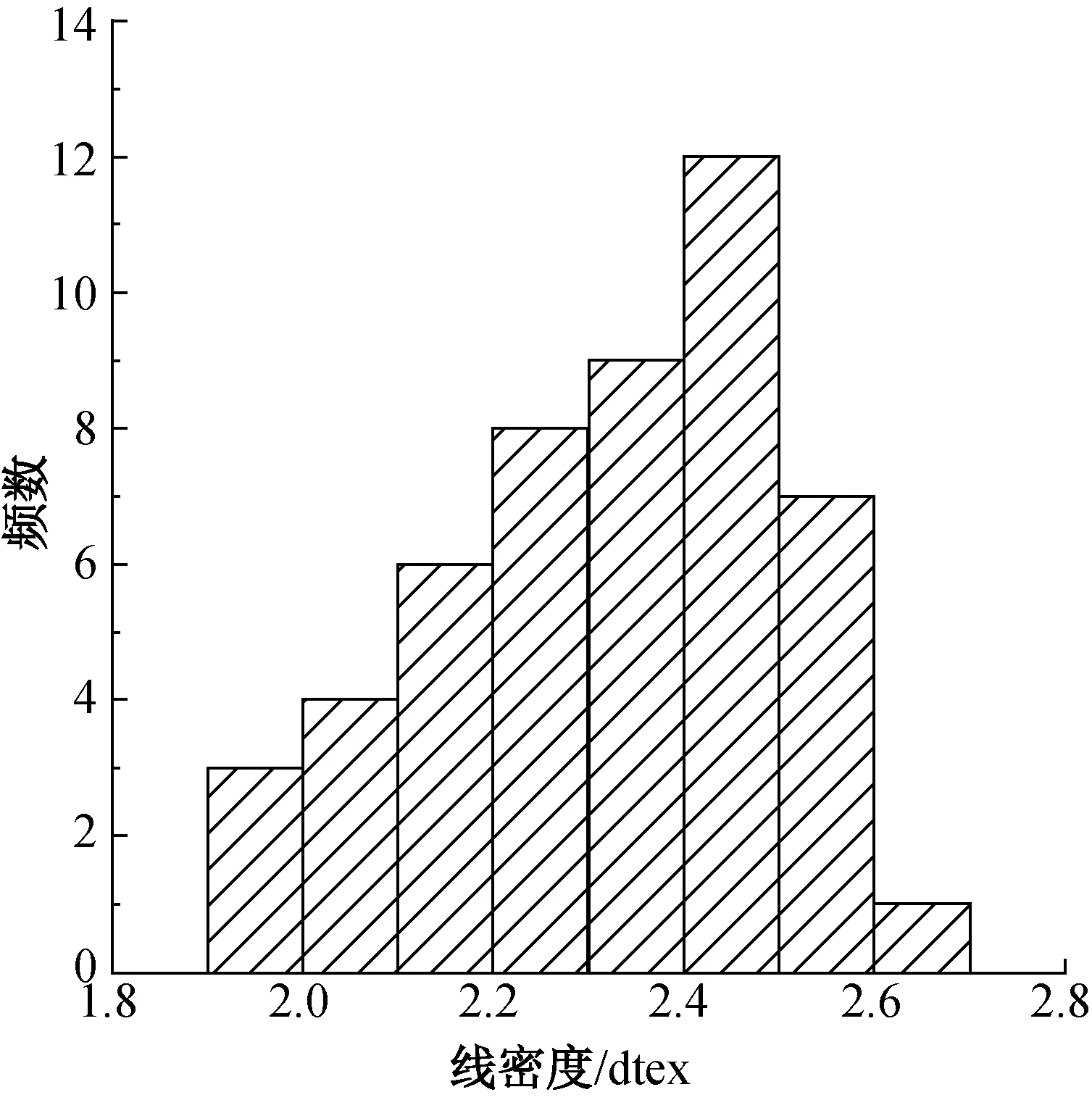
(a) Suplon?

(b) P84

(c) Yilun?

(a) Suplon?

(c) Yilun?

2.2 數據處理

當變量x(x≥0)服從均值為μ(μ>0)、標準差為σ(σ>0)的正態分布時，其累計分布函數FN(x)可表示為：

(1)

式中，Ф為拉普拉斯算子。

在基于“弱環理論”串聯模型建立的Weibull分布模型中，兩參數Weibull分布模型和三參數Weibull分布模型在纖維、紗線拉伸強度或強力分布的描述時應用最為廣泛[13-17]。

三參數Weibull分布模型同時具有位置參數γ(γ≥0)、尺度參數β(β>0)和形狀參數α(α>0)，通常可較好地擬合正態和對數正態分布，并與正態分布之間存在解析關系[18]。當變量x符合三參數Weibull分布時，累計分布函數F3P(x)：

(2)

當γ=0時，三參數Weibull分布簡化為兩參數Weibull分布，其累計分布函數F2P(x)：

(3)

兩參數Weibull分布模型可利用概率圖法進行模型參數的估計，而三參數Weibull分布模型，因同時存在3個模型參數，其參數估計具有相當的難度，通常采用極大似然法、雙線性回歸法、概率權重矩法、相關系數優化法以及灰色估計法等，不同的參數估計法其適用范圍和精度存在差異[19]。

為便于模型參數的估計，本文基于實測數據，采用Easyfit數據分析軟件對分布模型進行參數估計，并基于K-S檢驗法對分布模型的擬合優度進行檢驗。數據分析軟件對實測數據進行擬合時，自動獲得表征擬合優度的p值。通常，通過比較p值與顯著性水平a之間的大小關系來判斷選用分布模型接受與否。當pa時，認為樣本來自的總體與指定的分布無顯著性差異，即可認為該模型可用于描述測試結果的概率分布。通常認為當p>0.05時，選用的分布模型可用于描述樣本的分布特征，且p值越大，與選用的分布一致性越好。

2.3 分布擬合結果

3種短纖維的線密度和拉伸強度的擬合參數及p值列于表1和表2中。從擬合優度的角度而言，本文選用的3種分布模型在描述纖維線密度和拉伸強度分布時的p值均大于0.05，可認為上述分布模型均可用于描述聚酰亞胺短纖維的線密度和拉伸強度概率分布特征。但從擬合最優的角度而言，Suplon?短纖維的線密度分布采用兩參數Weibull分布最為合理，而P84和Yilun?短纖維的線密度分布采用三參數Weibull分布最為合理；Suplon?和Yilun?短纖維的拉伸強度采用兩參數Weibull分布最為合理，而P84短纖維的拉伸強度采用三參數Weibull分

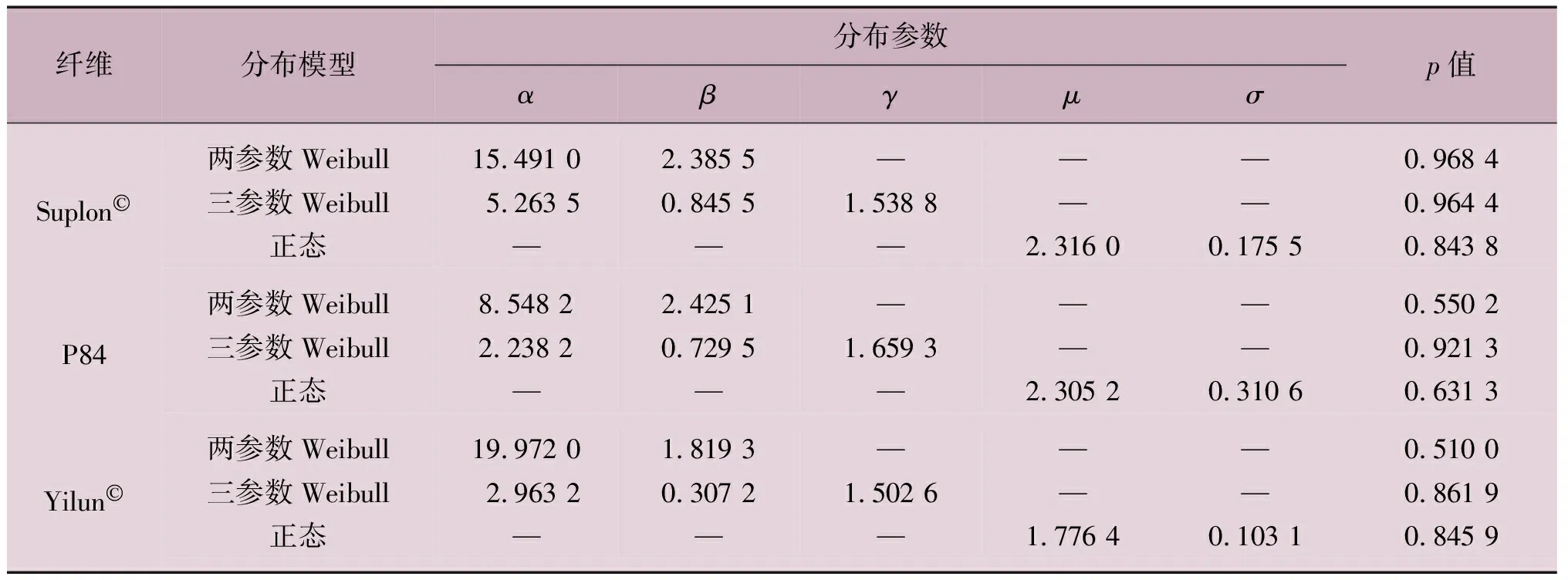
表1 線密度分布參數估計

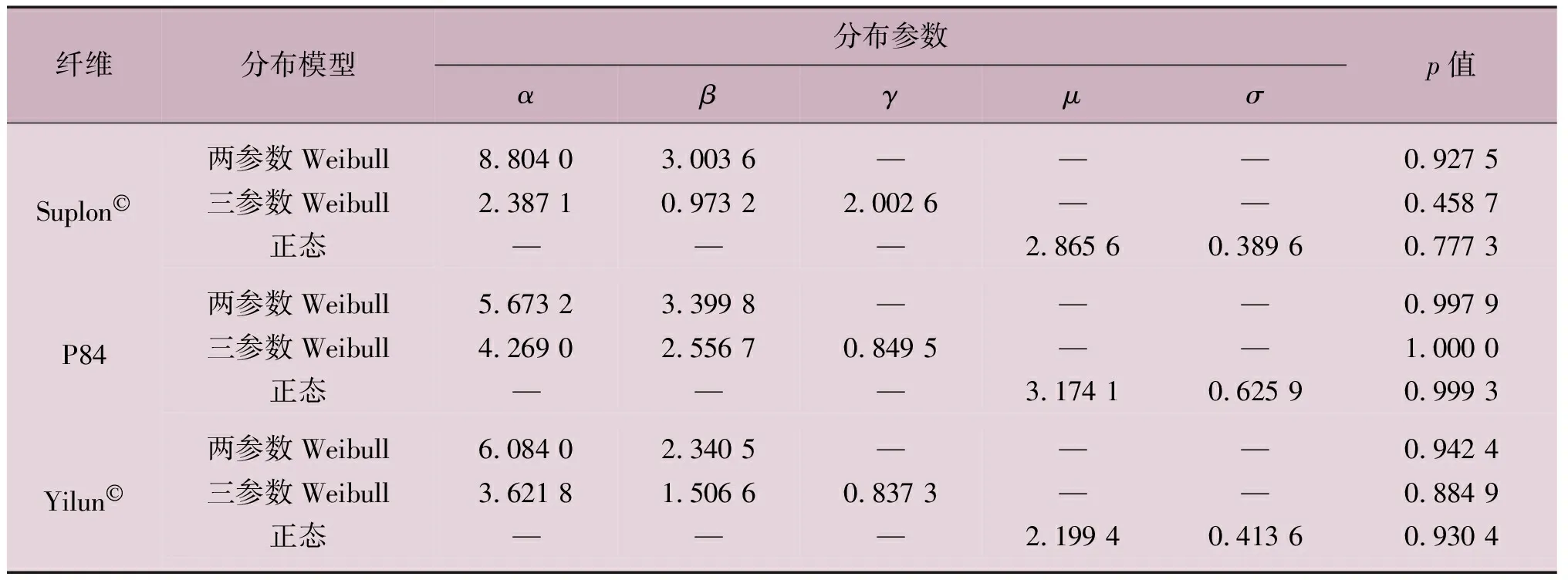
表2 強度分布參數估計

布最為合理。

值得關注的是，擬合數據是分布模型的最基本條件，Weibull認為隨機變量的分布函數并無任何理論基礎，通常基于選用的分布模型函數進行參數估計并檢驗擬合優度，直到找不到一個更好的模型函數為止[20]。故在研究分布模型時，均以獲得最佳的擬合優度為基礎，提出或修正某一分布模型。因此，如何選擇既有理論基礎，又具有較好擬合優度的分布函數，值得深入研究。

3 結論

本文基于原位測量法，對3種聚酰亞胺短纖維的線密度和拉伸強度進行了測量，并對纖維線密度和拉伸強度的概率統計分布進行了擬合分析和檢驗分析。結果表明：Suplon?短纖維的線密度和拉伸強度分布采用兩參數Weibull分布描述較為合理，P84短纖維的線密度和拉伸強度分布采用三參數Weibull分布描述較為合理，而Yilun?短纖維分別采用三參數和兩參數Weibull分布來描述其線密度和拉伸強度分布較為合理。