初探“順反粘數”

馬思琪

翻開《新高考（高二版）》2017年第9期，看到刊首《閑人莫入》一文給出了以下一組神奇的等式，引起了我的興趣：

82-42 =48；

682-342 =3468；

668 2-3342 =334 668；

6668 2-33342 =33 346 668；

……

文中說：“這樣的等式，可以一直寫下去，直到無窮大，統統都是成立的”，“迄今為止，這樣的一系列無窮等式，除此之處，別的地方再也沒有看到過，真正說得上‘只此一家，別無分店了！”

我想：這組等式長得這么美，為什么會那么“孤獨”呢？是她太“高冷”了嗎？還是“曲高和寡”呢？難道沒有相似的同伴？

我好想給她找個伴！

我找啊找，可就是找不到和它規律一樣的數，但我找到了她的姐妹花——并蒂蓮，請看：

142-72 =147：

134 2-672 =13 467；

1 334 2-6672 =1 334 667；

13 334 2-66672 =133 346 667；

……

這兩組數，是不是怎么看都有謎一樣的蹊蹺呢？

我為什么會發現這組等式呢？——國慶長假，全國各地到處各種堵，我就宅在家里來了一次有趣的數字發現之旅——這是一次奇特的旅游！以下是這一次的“游記”：

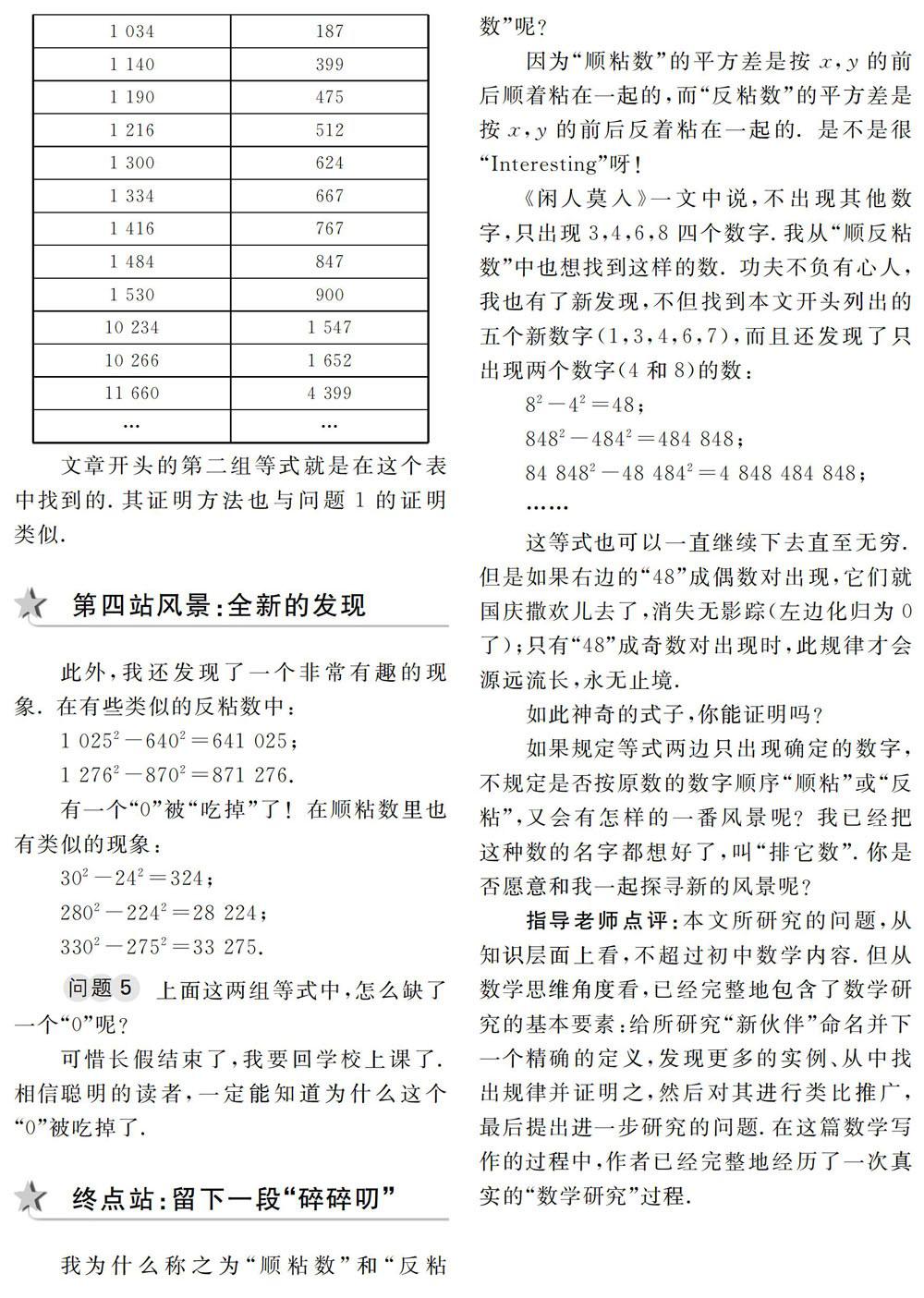
第一站風景：原題的證明

第二站風景：原題的推廣

第三站風景：原題的類比

第四站風景：全新的發現

如此神奇的式子，你能證明嗎？

如果規定等式兩邊只出現確定的數字，不規定是否按原數的數字順序“順粘”或“反粘”，義會有怎樣的一番風景呢？我已經把這種數的名字都想好了，叫“排它數”.你是否愿意和我一起探尋新的風景呢？

指導老師點評：本文所研究的問題，從知識層面上看，不超過初中數學內容.但從數學思維角度看，已經完整地包含了數學研究的基本要素：給所研究“新伙伴”命名并下一個精確的定義，發現更多的實例、從中找出規律并證明之，然后對其進行類比推廣，最后提出進一步研究的問題.在這篇數學寫作的過程中，作者已經完整地經歷了一次真實的“數學研究”過程.