基于MEMS/UWB組合的室內定位方法

郁嘉宇，趙 忠，李 凡，黃思文

(西北工業大學自動化學院，西安 710072)

0 引言

隨著人們生活水平的不斷提高，各種通信和定位技術也在不斷發展和完善，復雜的道路網絡和空間結構帶給人們生活和工作的壓力，使得人們對定位的需求愈加強烈[1]。根據范圍和場景，定位可分為室內定位和室外定位。室外定位技術主要借助于全球導航衛星系統(Global Navigation Satellite System, GNSS)，利用衛星和移動對象之間的直接通信，可完成精確定位[2]。而對于室內場景，GNSS信號易受遮擋，無法實現定位。

現已出現多種室內定位解決方案，包括紅外線、射頻識別、視覺、WiFi、藍牙信標(如iBeacon)、超聲波、LED信標、地磁場、超寬帶(Ultra-Wide Bandwidth, UWB)及微慣性器件等定位技術[3-4]。它們都有各自的優勢和不足。

UWB定位系統具有功耗低、抗多路徑效應效果好、安全性高、信號穿透力好等優點；但其不提供姿態信息，動態范圍和魯棒性較差，對外界硬件設施依賴程度較高，存在信號遮擋(鐵材料和結構復雜的混凝土墻壁等)、信號作用距離有限、信號易被吸收和成本高等問題。微機電系統(Micro-Electro-Mechanical System，MEMS)定位精度與慣性器件本身精度密切相關，不易受環境干擾、獨立工作能力強、短期精度高，可以準確測得定位目標的運動參數，但其定位誤差會隨時間增長[5-6]。當下MEMS慣性傳感器朝著低成本、低功耗、高精度的方向發展，在室內定位領域將會有更大的應用空間。

UWB與MEMS定位在全球范圍內受到了廣泛關注與深入研究。劉見輝等提出了慣性導航系統(Inertial Navigation System，INS)和掃描儀相結合的測量系統，同時在該量測系統中又加入了UWB以解決INS誤差積累的問題[7]。鄔春明等結合差分全球定位系統(Differential Global Positioning System，DGPS)和UWB，利用Kalman濾波器消除UWB非視距誤差，采用粒子濾波器進行數據融合，可將整體定位精度提高19%[8]。王芳等采用UWB與里程計信息融合的定位技術，提高了里程計航位推算穩定性與精度[9]。Qigao Fan等通過建立INS/UWB融合濾波的誤差模型，提出了模糊適應卡爾曼濾波(Fuzzy Adaptive Kalman Filter，FAKF)，根據模糊控制理論對量測噪聲進行調整[10]。Ascher C等將UWB和INS進行緊組合，利用INS得到用戶的軌跡和航向信息，結合UWB精確的定位數據，可完成室內環境下的實時定位[11]。

本文旨在將UWB和MEMS兩種技術相結合，采用合適的算法對兩系統進行信息與數據融合，充分發揮兩者在室內定位中的優勢，解決UWB系統由于外在因素無法完成有效定位、MEMS長期定位精度差等問題。本文所構建的混合定位系統，在復雜室內環境下定位的連續性、穩定性和可靠性得到大大增強[12]。此外，成本較高的UWB定位設備也會因低成本MEMS的加入使得成本有所下降，在保證定位精度的前提下，UWB定位基站的布設成本也會有所降低。

1 基礎定位系統

1.1 UWB定位系統

UWB定位技術源于超寬帶無載波通信技術，其利用納秒至微秒級的非正弦波窄脈沖進行通信，工作頻段為3.1～10.6GHz，可直接脈沖調制，不受載波干擾[13]。UWB定位在本質上與GPS衛星定位原理一致，即自己搭建基站，利用發射的UWB脈沖信號進行測距或者定向，然后根據和GPS定位類似的算法，計算出每個基站到移動站(定位標簽)的距離，從而解算出移動站的空間坐標。UWB定位簡易示意圖如圖1所示。

系統主要由定位基站(也稱接收機)、定位標簽和中心處理器組成[13]。

按照測量參數不同，將UWB定位方法分為基于接收信號強度法(Received Signal Strength Indication, RSSI)和基于到達角度法(Angle of Arrival, AOA)、基于到達時間法(Time of Arrival, TOA)和基于到達時間差法(Time Difference of Arrival, TDOA)等[14-16]。本文采用AOA/TDOA算法，充分利用距離或角度信息，其原理如圖2所示。

傳感器能得到定位目標的到達時間差Δt和到達角度α1和α2，設移動站MS(x0,y0)、基準站BS1(x1,y1)和BS2(x2,y2)，則

(1)

其中，c代表光速。聯立式(1)兩式即可求得MS的二維坐標。對于三維情況，TDOA公式與二維類似，如式(2)所示。

(2)

AOA包括方向角λ和仰角φ，如式(3)所示。

(3)

本文所使用的AOA/TDOA算法，避免了TOA方法嚴格時鐘同步問題，采用了天線陣列，雖然設備相對比較復雜，但是精度得到了保證。每個傳感器探測一個標簽的二維到達角度(AOA，方向角和仰角)，同時記錄下感應的TDOA，從傳感器得來的數據可通過相應的算法綜合起來使用，從而得到定位結果。

1.2 MEMS慣性定位系統

首先介紹本文坐標系的定義及坐標系間的轉換關系。載體坐標系(b系)是指在定位過程中載體位置處的坐標系，本文所指b系原點在載(車)體重心，x軸沿載(車)體橫軸向前，y軸沿載(車)體向左，z軸沿載(車)體豎直向上，如圖3所示。

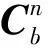
(4)

MEMS慣性定位算法由初始對準和定位解算兩部分組成，前者為后者提供初始姿態信息[17]。對慣性系統而言，其MEMS陀螺精度太低以至無法感測地球自轉角速度(約15(°)/h)，因而低精度MEMS捷聯慣導系統初始自對準無法完成方位對準，只能根據加速度計輸出解算出載體俯仰角和橫滾角[17]，即水平對準。方位對準則需要利用其他外部信息給出。

(1)水平初始對準

靜基座條件下，重力加速度只在地垂線方向上有輸出(輸出為g)，有：

(5)

(6)

(2)方位初始對準

對于初始航向角，若以地理坐標系為導航坐標系，則初始航向角是指與真北的夾角，此角度需要磁力計或磁羅盤等提供；若以地面正交坐標系為導航坐標系，則直接裝訂初始方位角為0°，最終解算出來的坐標即為該坐標系下的結果。對于初始航向問題，本文采用直接裝訂的方式，將初始時刻計算得到的磁航向作為系統初始航向裝訂。

(3)定位解算和反饋校正

圖4所示為慣導解算過程的詳細框圖，主要顯示了根據陀螺儀和加速度計輸出計算車輛最終姿態、速度和位置的過程。

相關算法和公式如下所述[19]：

設計15維Kalman濾波器，其狀態向量對應為：

(7)

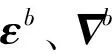
KF估計出來的這些誤差量將被反饋到三軸陀螺儀、三軸加速度計、常規慣導解算的姿態、速度和位置，通過修正得到更為精確的定位結果。

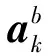
(8)

根據補償后的陀螺輸出對姿態矩陣進行更新：

(9)

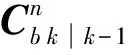
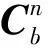
(10)

由于MEMS器件采樣頻率較高，故可認為在極短的時間內受到一個恒力，載體做勻變速直線運動。用梯形算法計算速度和位置，公式如下：

(11)

前2個部分得到的姿態、速度、位置信息是慣導解算直接得到的信息，誤差會隨時間的增加而累積，故需利用KF估計量對其進行進一步修正：

(12)

通過KF得到的3個的姿態角誤差(小角度)對姿態矩陣進行修正：

(13)

(14)

(15)

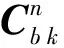
(16)

其中，arctan2(a，b)為反正切函數，值域為(-π，π)，與橫滾角、航向角定義范圍一致。

2 Kalman濾波器設計

2.1 動態零速修正

假設小車在勻速、剎車、加速、轉彎等不同運動狀態過程中，不發生側滑與跳躍，則可以認為車輛的天向與側向速度在車體運動中始終保持為零，即存在動態零速：

(17)

可以利用車輛的天向速度與側向速度為零的速度信息，輔以里程計輸出的軸向速度信息與慣導解算得到的速度信息作差，估算捷聯解算的誤差信息，進行反饋修正，從而提高定位精度。

以15維狀態向量為例，狀態量取慣導系統的3個姿態誤差角、3個速度誤差、3個位置誤差，三軸陀螺常值漂移、三軸加計常值偏置，如下所示：

(18)

(19)

定位算法簡化后的誤差模型：

(20)

根據定位算法的誤差模型和Kalman狀態量的選擇，可以得到狀態轉移矩陣為：

(21)

(22)

根據量測向量的選取，可得到對應的量測矩陣：

(23)

通過狀態量的估計，完成Kalman濾波的估計與補償，可以得到最終的定位結果。

2.2 MEMS/UWB融合濾波器設計

根據實際UWB系統的輸出信息以及所采用的MEMS定位算法，本文最終采用KF松組合方式實現兩系統的融合定位[7，20-22]。單獨的車載MEMS定位系統，是采用帶動態零速修正的慣導解算算法，利用實際解算速度和里程計速度動態零速構造量測信息對慣導誤差進行修正，此過程通過KF實現。

對于捷聯慣導而言，以速度誤差為觀測量進行狀態估計與反饋，進而抑制慣導誤差積累，此過程不依賴于外界其他硬件設施。對于MEMS/UWB融合而言，在MEMS基礎上加入了UWB位置信息，需要構造位置誤差觀測量再進行KF。考慮到2個系統的獨立性，組合結構圖如圖5所示。

在上述2個KF當中，考慮到其狀態量相同，只是量測信息有所不同，因此時間更新相似，可根據條件判斷選擇對應的量測更新。因此，2個KF估計器是可以合并的。對圖5進行合并，可得到MEMS和UWB的松組合方式的結構框架如圖6所示。

由UWB提供位置信息P以及里程計信息與動態零速信息，形成六維量測向量：

(24)

其中：Δpk=pINS-pUWB,Δvk由式(19)可得，則其對應的量測矩陣為：

(25)

3 試驗與分析

本文中在7.5m×7.5m×3m的實驗室里布設4個UWB定位傳感器，大致布局如圖7所示。

UWB標簽固定在小車頂部，MEMS慣性傳感器固定在小車中心。UWB標簽示意如圖8所示。 MEMS器件選用ADI公司的ADIS6448十軸慣性器件，其外形如圖9所示，參數如表1所示。

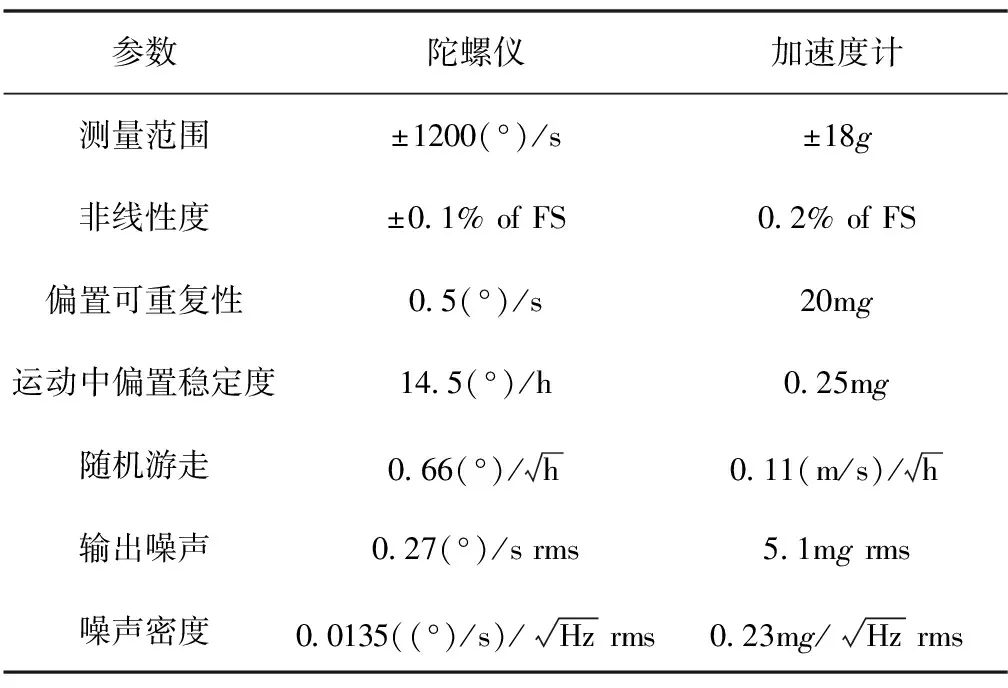
表1 ADIS16448主要參數(A+G)

本文試驗的路線設計為U型運動路線，便于分區間進行誤差計算和定位精度分析。往返一次試驗路徑為A-B-C-D-C-B-A，軌跡示意如圖10所示。

重復10次U型往返路徑作為融合試驗路徑。整個試驗的運動時間為348.2860s，運動距離為253.4369m。

融合過程中，由于MEMS解算周期與UWB位置輸出周期不一致，并且兩者周期存在非整數倍關系，所以需要考慮長時間解算的時鐘同步性問題。MEMS輸出頻率為102.4Hz，UWB輸出頻率為9.25Hz，根據兩者的時間關系，每20s進行一次數據調整。一次調整時間偏差從0.1270s減小到0.0195s。時鐘同步性調整如圖11所示。

MEMS、UWB、MEMS/UWB三者定位效果如圖12～圖14所示。

由圖12可以看出，MEMS定位結果平滑，但隨著時間的積累，由于航向誤差的存在與不斷積累，解算路徑慢慢偏離實際運動路徑，誤差逐漸增加。

由圖13可以看出，UWB屬于絕對定位，其誤差在一個合理的范圍內，整體運動軌跡在實際運動軌跡的兩側跳動分布。由圖14可以看出，MEMS/UWB融合定位因為有了UWB位置信息的加入，對MEMS的積累誤差有著明顯的抑制作用，可以得到近似于UWB定位的效果。對于UWB而言，該融合算法在UWB定位系統出現定位失效的情況下，仍能保持比較好的定位效果。表2所示為三種定位方式的終點坐標以及誤差情況。

表2 融合定位試驗的終點坐標及誤差對比結果

由表2可以看出，融合定位對MEMS定位的積累誤差有著顯著的修正和抑制作用，將相對誤差從0.2401%降到0.0265%。而UWB自身定位精度較高，融合對UWB定位精度無顯著提升作用，但對UWB定位易受遮擋的缺陷有著很好的彌補作用。整體而言，MEMS/UWB融合定位可適當彌補兩者的缺陷，擁有比單獨MEMS子系統更好的定位效果。

4 結論

本文以室內定位為背景，針對UWB定位存在易受環境影響與遮擋的問題和MEMS定位中誤差隨時間積累的問題，文中完成了以下工作：

1)設計了以里程計速度信息和動態零速作為觀測量的MEMS慣導解算算法，通過卡爾曼濾波器抑制慣導的誤差積累，實現了短期誤差在1%以內的定位效果。

2)通過分析UWB和MEMS這2個定位子系統，在MEMS定位算法的基礎上，完善量測方程，建立速度、位置六維量測方程，完成MEMS/UWB融合算法的設計，實現兩者的融合定位。

3)針對融合過程中MEMS與UWB時鐘不同步的問題，提出了定時調整方法，減小時鐘不同步帶來的誤差。

本文提出的MEMS/UWB組合的室內定位方法實現了兩者的優勢互補，解決了MEMS定位長期發散問題與UWB定位短期失效問題。MEMS/UWB融合定位擁有比單獨子系統定位更好的定位精度與魯棒性。