任意光滑截面橋墩地震動水壓力分析

王丕光， 趙 密， 杜修力

(1.北京工業大學 城市與工程安全減災教育部重點實驗室，北京 100124；2.清華大學 土木工程系，北京 100084)

隨著世界經濟的發展，各國均投入巨資興建跨越江海的大跨度深水橋梁工程，我國已經修建的大規模的跨江跨海工程長大橋梁中許多橋梁處于深水之中[1]。這些橋梁工程多數位于地震區，在地震作用下橋墩與周圍水體的動力相互作用會對橋墩產生動水壓力，研究表明該動水壓力會對深水墩柱結構和橋梁結構的動力反應產生較大影響[2-6]。橋梁作為生命線工程，一旦遭受地震破壞將會產生無法估量的后果。因此充分認識地震作用下橋墩與周圍水體的動力相互作用，對于新建深水高墩橋梁抗震設計和已建橋梁抗震安全評估具有重要的意義。

實際工程中，存在各種截面形式的墩柱結構，如圓形、矩形、橢圓形和圓端形等。針對圓形橋墩，Tanaka等[7]利用解析法分析了水平地震作用下齊水面彈性圓柱體單位長度上動水壓力的附加質量系數和阻尼系數；賴偉等[8]提出了一種圓形橋墩上地震動水壓力的半解析半數值方法；Li等[9]提出了圓形空心橋墩上地震動水壓力的簡化計算公式；黃信等[10-11]討論了自由表面波、水體壓縮性和水底吸收邊界對圓形橋墩地震動水壓力的影響；杜修力等[12-13]提出了可壓縮水體條件下圓形橋墩地震動水壓力的時域算法和時域簡化公式。另外，劉振宇等[14-15]提出了矩形空心橋墩地震動水壓力的計算公式。上述情況表明，目前對于地震作用下圓形和矩形橋墩地震與周圍水體的動力相互作用問題已經取得了可供實際應用的研究成果，但還缺乏對橢圓形和圓端形等光滑截面形式橋墩地震動水壓力的研究。

本文針對地震作用任意光滑截面形式橋墩與周圍水體的動力相互作用問題，基于輻射波浪理論，根據水體控制方程和邊界條件，通過分離變量和傅里葉級數展開的方法，推導了任意光滑截面橋墩地震動水壓力的解析解。

1 控制方程及邊界條件

地震作用下任意光滑截面橋墩與水體動力相互作用的分析模型如圖1所示。假定地基為剛性，水體為無旋、無黏、可壓縮的小擾動流體。柱坐標系原點設于墩底并以x軸正方向為θ=0°方向，橋墩表面方程為r=a(θ)，橋墩高度為H，水深為h。地面運動沿x方向的位移為ug，橋墩的彈性位移為us，橋墩的絕對位移為u=ug+us。柱坐標系下，以動水壓力p作為未知量的水體控制方程為

(1)

式中:c為聲波在水中的傳播速度，不可壓縮水體條件下1/c=0。初始時刻，水體靜止。

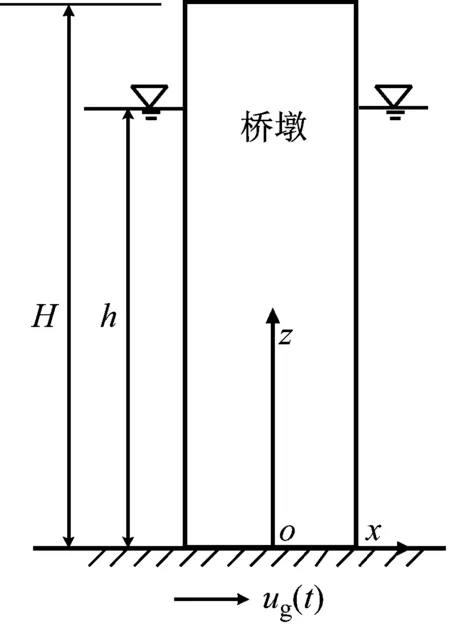
圖1 水中任意光滑截面橋墩分析模型Fig.1 Definition of the problem

水體底部、靜水表面、無窮遠以及水體與結構交界面邊界條件為

(2)

p=0z=h

(3)

p=0r→∞

(4)

(5)

式中:n為柱體表面任意點的單位外法線向量;α為n與x軸方向的夾角，則

(6)

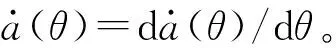
2 動水壓力的頻域解

地面簡諧運動時水體的動水壓力和橋墩的絕對位移可以表示為

p(r,θ,z,t)=P(r,θ,z)eiωt

(7)

u(z,t)=Ueiωt=(Us+Ug)eiωt

(8)

式中:ω為結構的振動頻率;Us和Ug分別為頻域下結構的彈性位移和剛體位移。柱坐標系下，P(r,θ,z)可分離變量為

P=R(r)Θ(θ)Z(z)

(9)

將式(7)代入控制方程式(1)，可得到三個解耦的方程

Θ″+n2Θ=0

(10)

Z″+λ2Z=0

(11)

(12)

式中:n和λ為待定系數。根據邊界條件式(2)～式(4)，可得到橋墩動水壓力P的表達式為

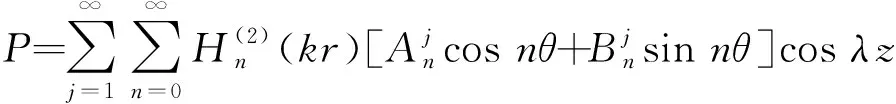
(13)

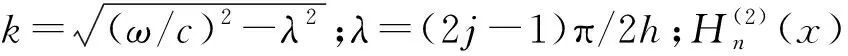
將式(13)代入邊界條件式(5)并整理得

(14)

其中,

(15)

(16)

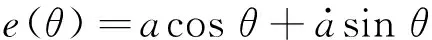
(17)

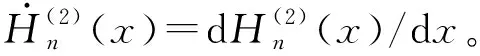
將式(14)等式兩邊同時乘以cosλz，并在區間[0,h]積分，利用特征函數cosλz的正交性可得

(18)

其中,

(19)

基于本文橋墩表面連續光滑的假定，可將函數e(θ),qjn(θ)和gjn(θ)展開成傅里葉級數的形式。e(θ),qjn(θ)和gjn(θ)傅里葉級數展開式分別為

(20)

(21)

(22)

將式(20)～式(22)代入式(18)整理得

?

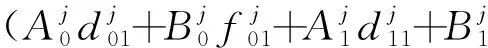
(23)

式(23)可重寫為如下矩陣的形式

NC=J

(24)

其中,

J={a0,b0,a1,b1,…}T

(25)

(26)

(27)

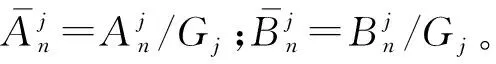
C=N-1J

(28)

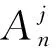
3 動水力及運動方程

地震作用下橋墩表面沿單位高度上的水平動水力為

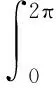
(29)

將式(13)代入式(29)整理得

F(z)=Fg+Fs

(30)

(31)

(32)

(33)

式中:Fg和Fs分別為地震作用下橋墩剛體運動和彈性運動引起的動水力。

假定橋墩為彎曲懸臂梁，將橋墩的彈性位移Us按無水振型展開為

(34)

式中:Xi(z)為橋墩的第i階振型；Yi(ω)為第i階振型坐標，地震作用下可按如下方程求解

-ω2MiYi(ω)+iωCiYi(ω)+KiYi(ω)=ω2UgDi+Fi

(35)

其中,

(36)

(37)

Ci=2ζiωiMi

(38)

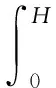
(39)

(40)

式中:A為截面面積;ρs為橋墩質量密度；ωi為第i振型對應的自振頻率;ζi為相應的阻尼比。

將式(31)和式(32)代入式(40)整理得

(41)

(42)

(43)

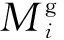
將式(37)、式(38)和式(41)代入式(35)整理得

(44)

將式(44)代入式(34)，通過傅里葉反變換可得到時域下橋墩的彈性位移為

(45)

4 數值算例

算例1旨在通過對剛性橋墩動水壓力的分析以驗證本文提出的任意光滑截面橋墩動水壓力計算方法的精度。分別通過本文方法和ABAQUS聲固耦合方法計算單位脈沖運動作用下剛性橢圓形和圓端形橋墩的動水力；對式(31)進行傅里葉反變換可得到剛性橋墩動水力的時域解。圖2是結構剛體運動位移，脈沖持時0.2 s，頻譜覆蓋了地震作用頻段；圖3為算例中橋墩的截面尺寸，圖中L1和L2的值分別取為20 m和30 m；水深取為80 m，水體聲速和密度分別為1 438 m/s2和1 000 kg/m3。

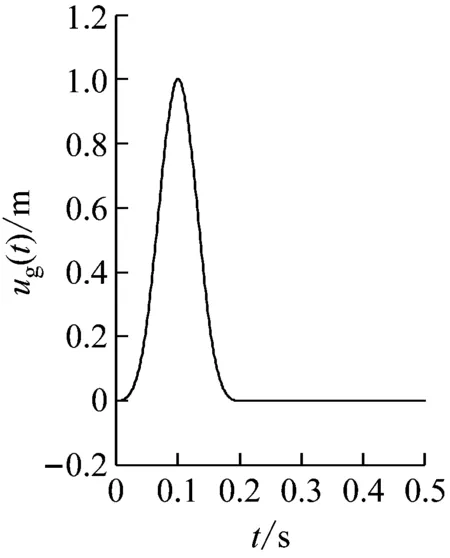
(a)時程

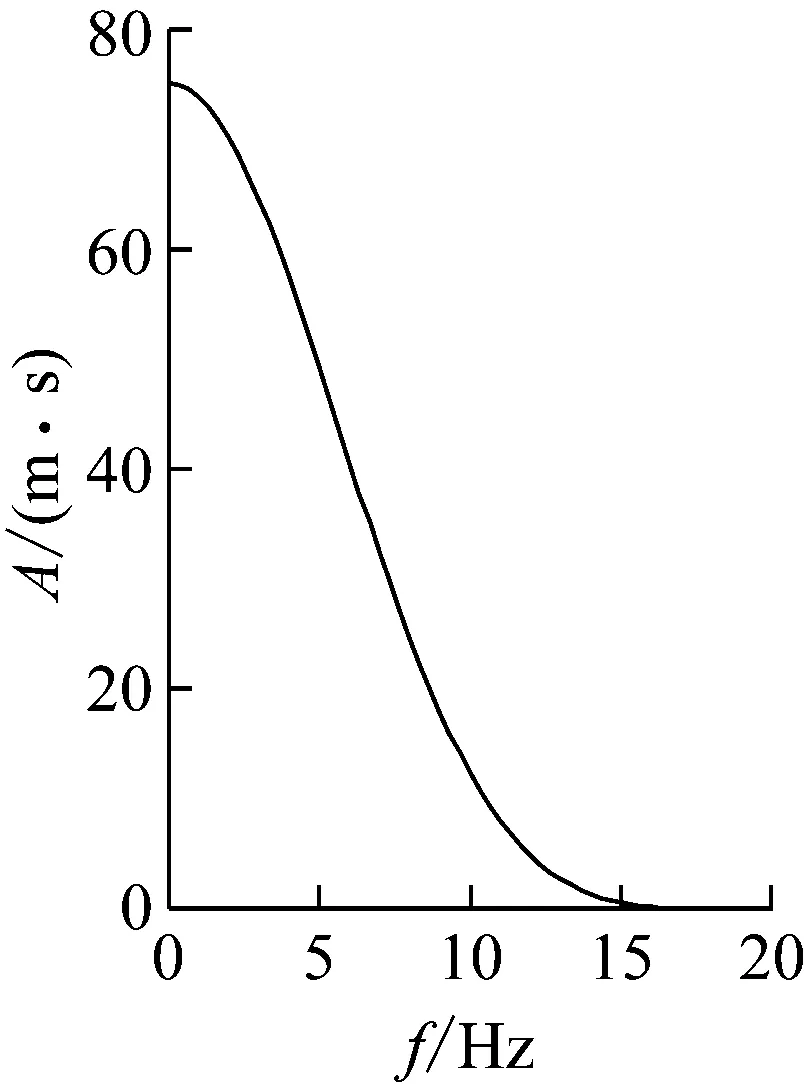
(b)傅里葉譜幅值圖2 剛性橋墩位移時程和傅氏譜Fig.2 The time history of displacement of rigid pier and its Fourier spectrum

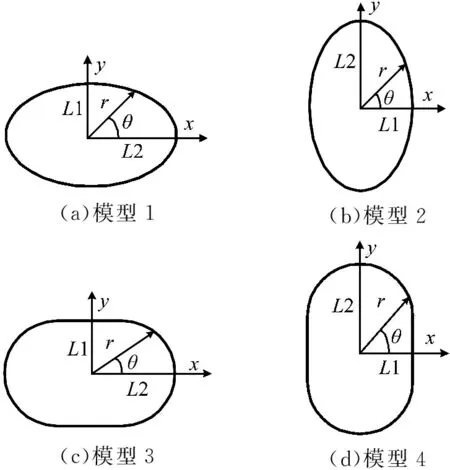
圖3 橋墩模型截面尺寸Fig.3 Cross-section of the piers

圖4為橋墩截面函數e(θ)的傅里葉級數展開解與精確解的比較；由圖中可以看出，精確解與傅里葉展開解吻合很好。可見，橋墩表面連續光滑函數的傅里葉級數展開具有很高的精度。圖5為沿橋墩高度積分的總動水力的本文方法與ABAQUS聲固耦合方法的比較；由圖中可以看出，兩種方法計算得到的結果一致；可見，本文方法具有很高的精度，并且避免了求解復雜的流體動力問題。

(a)模型1

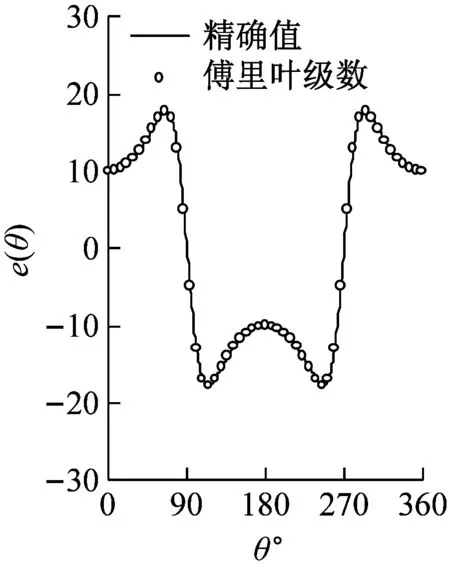
(b)模型2

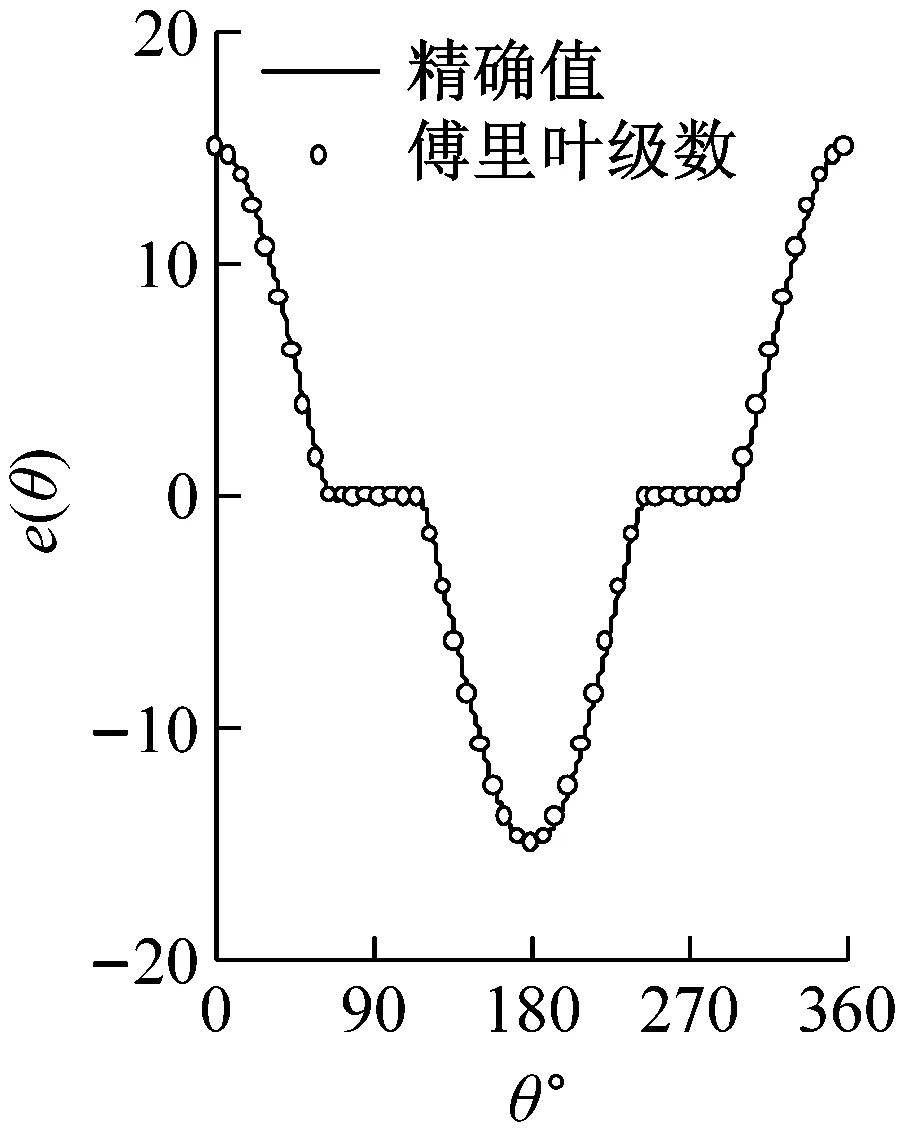
(c)模型3

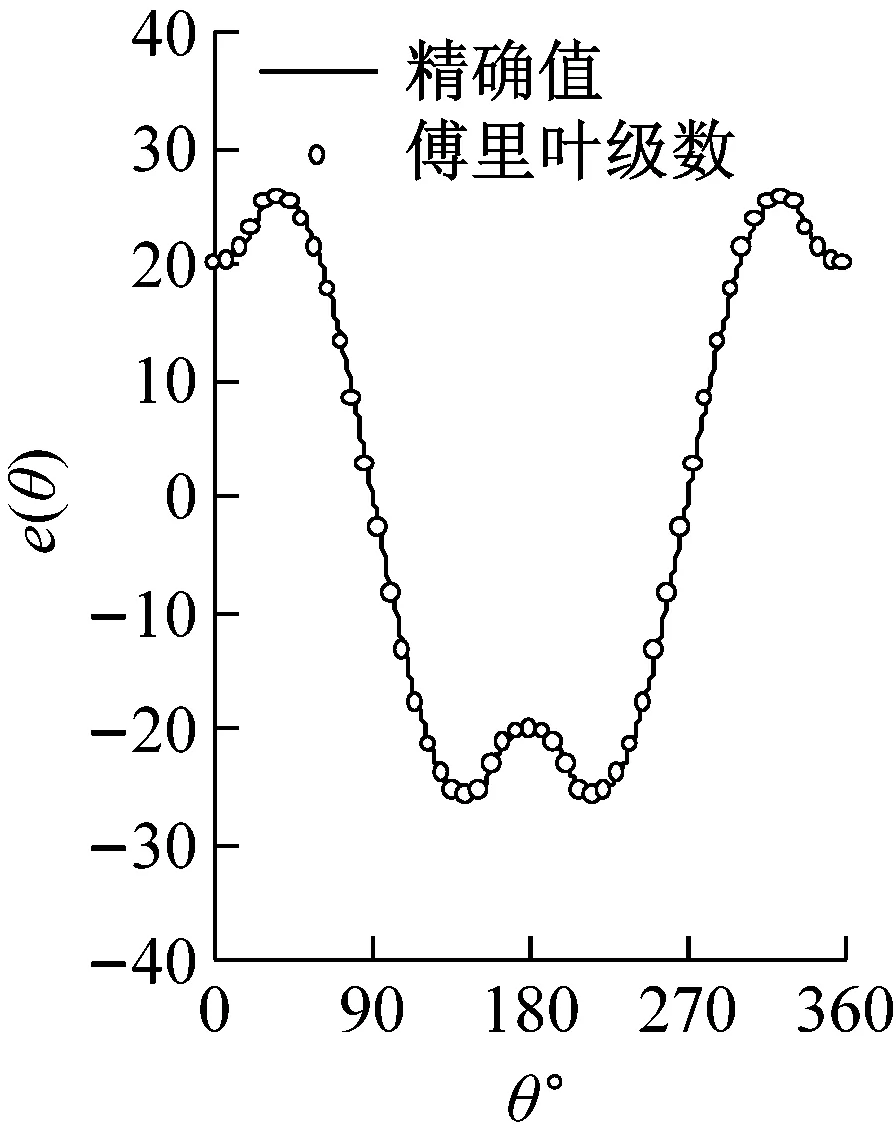
(d)模型4圖4 函數e(θ)的傅里葉級數展開Fig.4 Fourier expansion of the function e(θ)

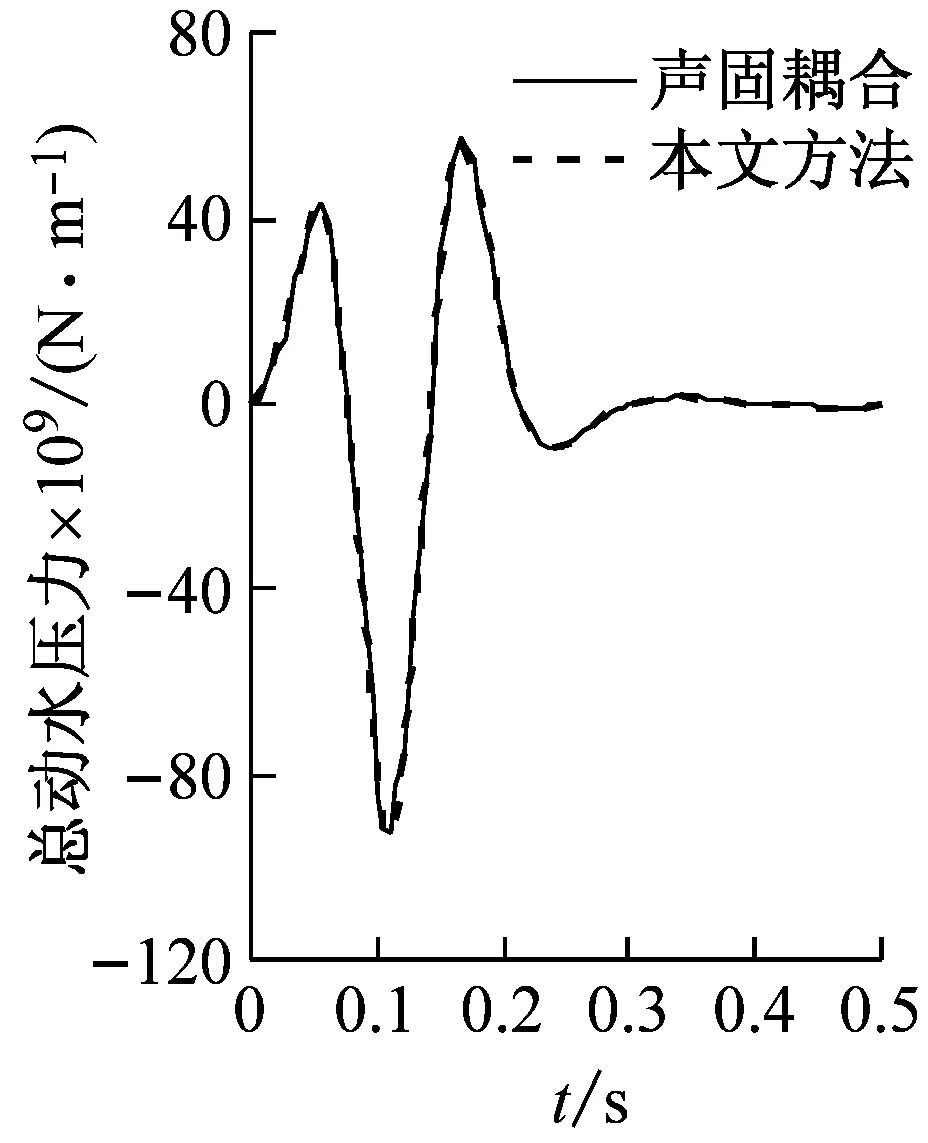
(a)模型1

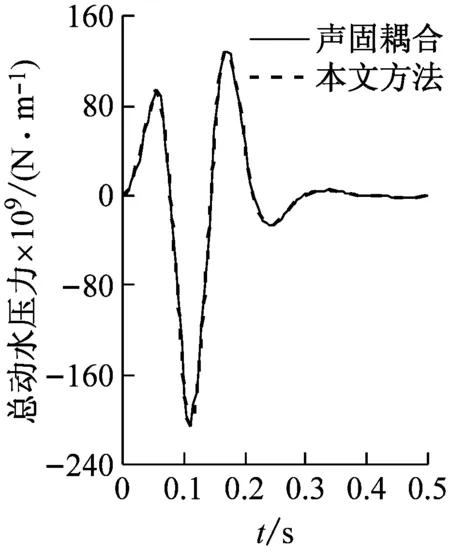
(b)模型2

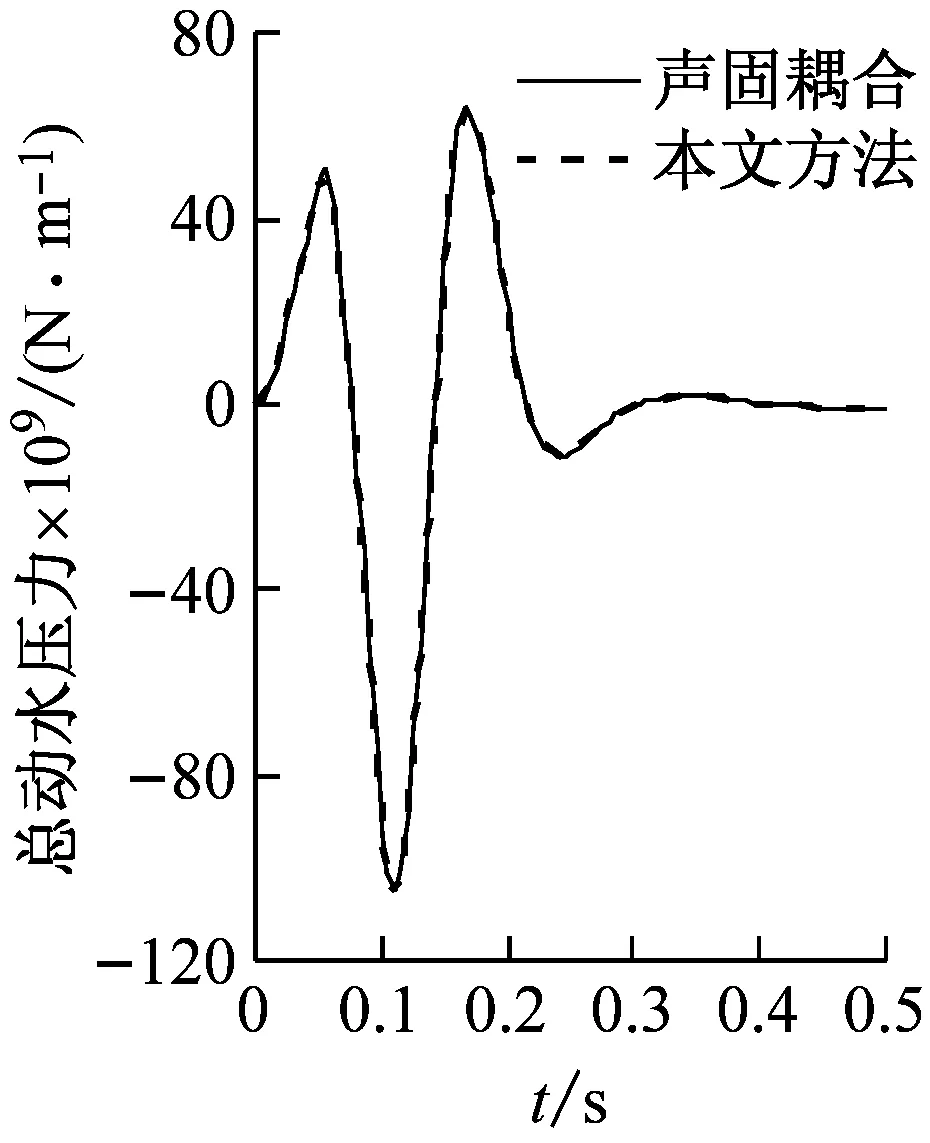
(c)模型3

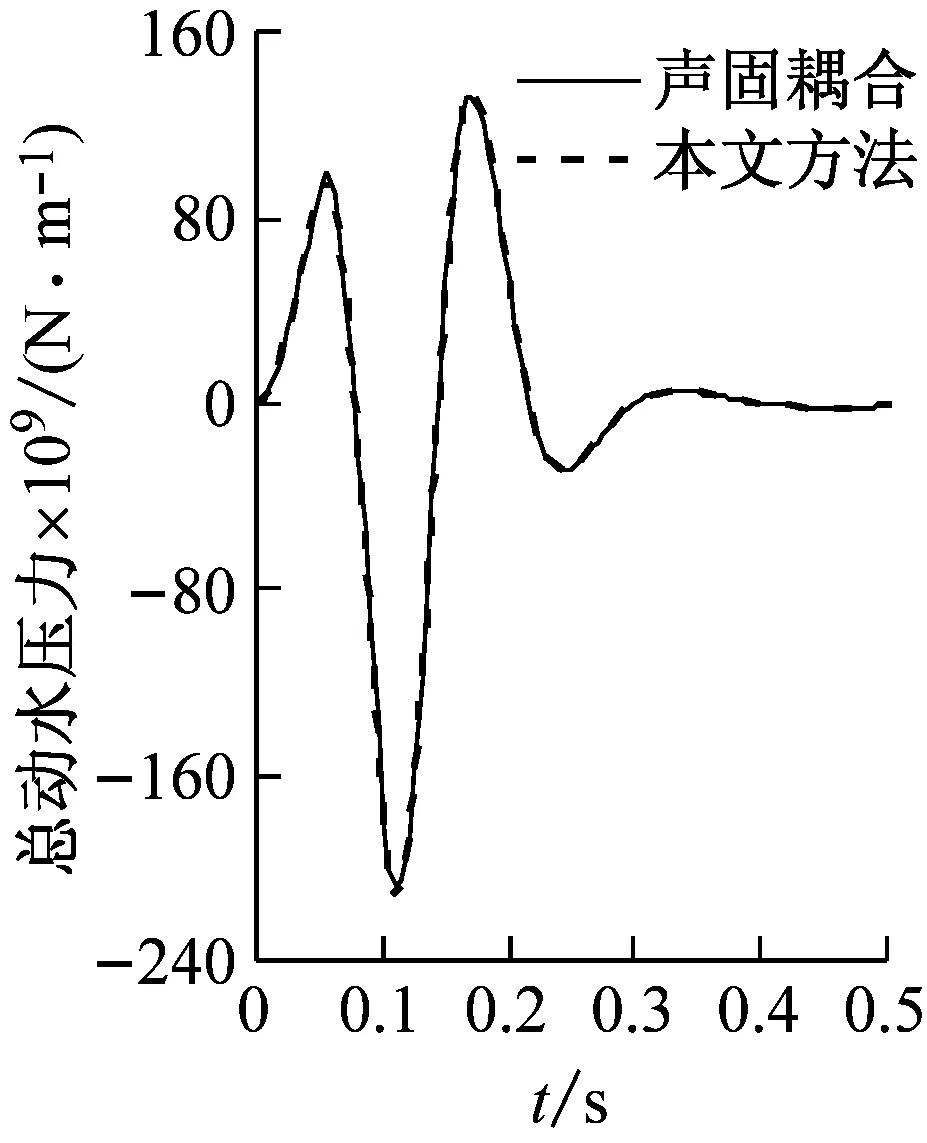
(d)模型4圖5 橋墩總動水力時程Fig.5 The time history of total hydrodynamic force on piers

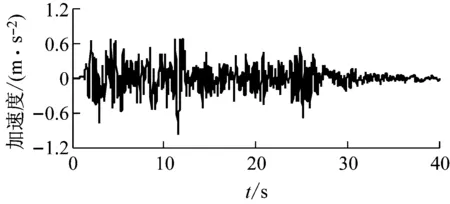
(a)

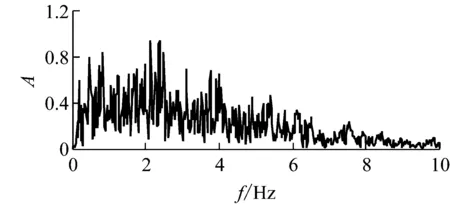
(b)圖6 El-Centro地震波加速度時程和傅氏譜Fig.6 The time history of acceleration of El-Centro wave and its Fourier spectrum

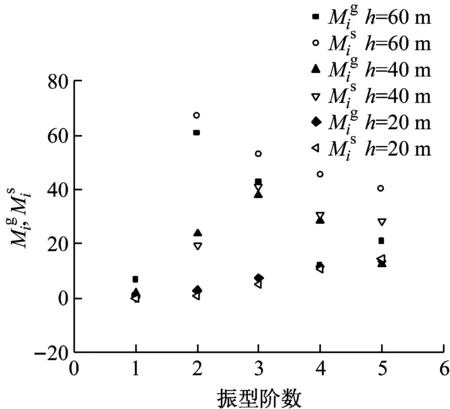
(b) 模型4圖7 動水力振型系數和Fig.7 The mode correlation coefficients and for the hydrodynamic force on the pier

5 結 論

本文基于流體輻射波浪理論，通過分離變量和將光滑連續函數展開成傅里葉級數的方法，推導了一種任意光滑截面橋墩地震動水壓力的解析公式，并基于彎曲懸臂梁模型給出了任意光滑截面橋墩動力反應的求解方法。剛性橋墩的結果表明，采用本文解析公式計算的橋墩地震動水壓力與聲固耦合數值方法的計算結果吻合很好，證明了任意光滑截面橋墩地震動水壓力解析公式的正確性。彈性橋墩的結果表明，地震動水壓力增大了橋墩的動力反應，并且水深與橋墩高度的比值是決定動水壓力影響大小的一個主要因素；當比值較大時動水壓力對橋墩地震反應影響較大，不可忽略，這一點在深水橋梁的設計中必須注意。

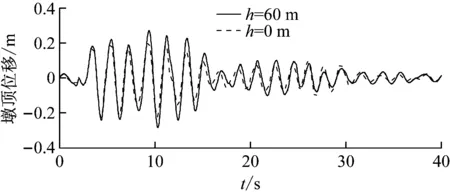
(a) 模型2

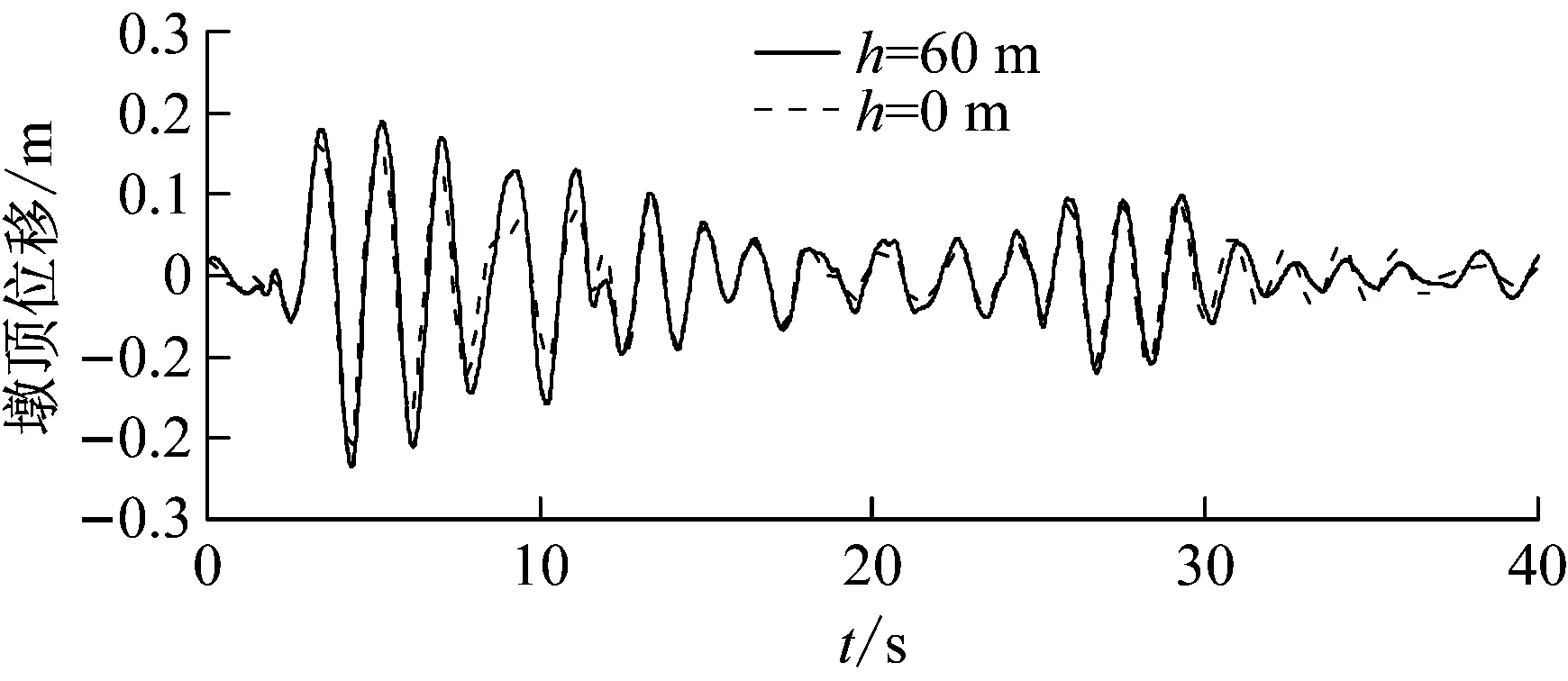
(b) 模型4圖8 墩頂位移時程Fig.8 The time history of displacement on top of the pier

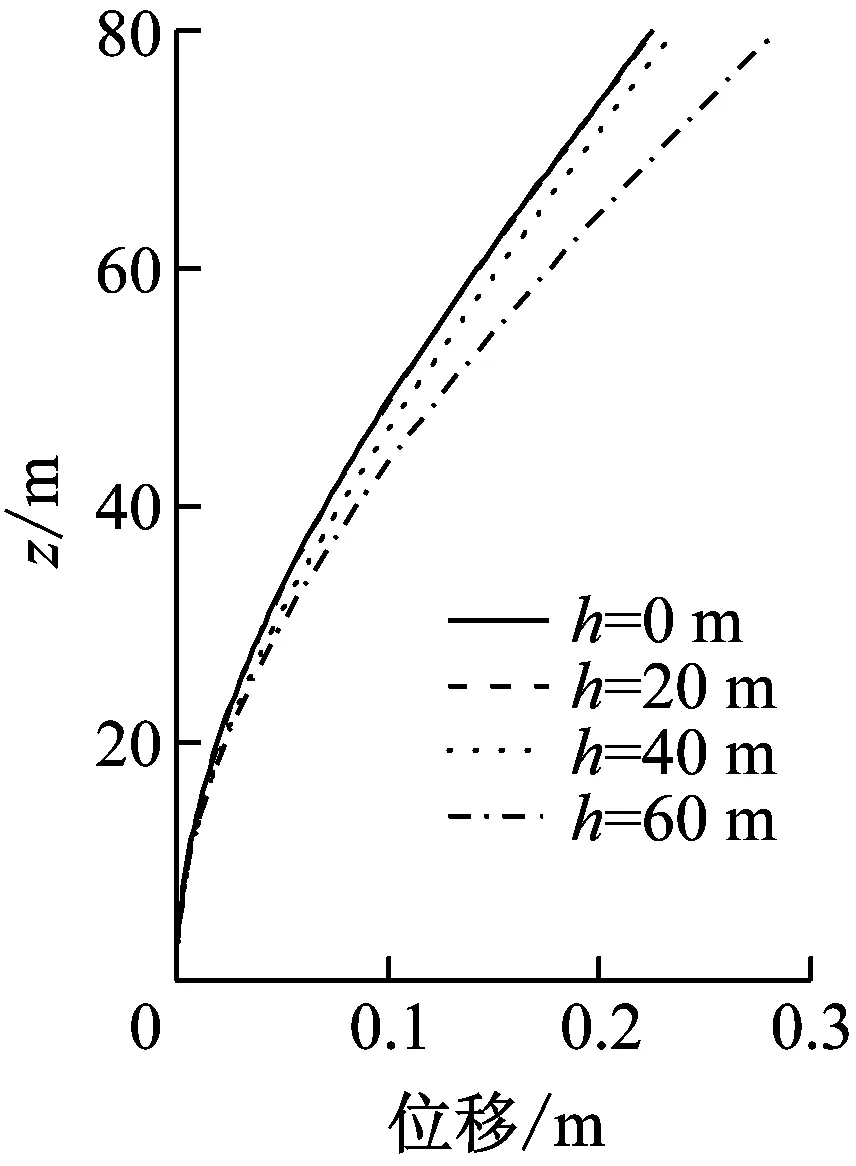
(a) 模型2

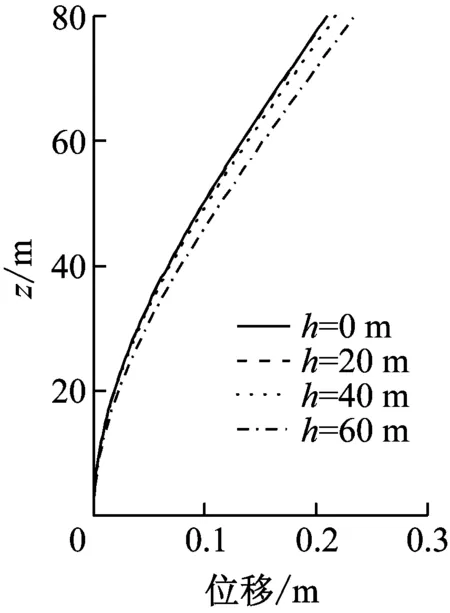
(b) 模型4圖9 墩身峰值位移Fig.9 Peak displacement along the vertical direction