考慮隨機幾何初始缺陷的儲油罐抗震可靠度分析

徐亞洲， 婁燕芳

(1.西安建筑科技大學 土木工程學院，西安 710055;2.濮陽職業技術學院，河南 濮陽 457000)

儲油設備常采用圓柱形立式儲油罐形式，地震作用下易發生破壞，進而引發水體污染、火災等次生災害，造成嚴重的經濟損失和環境污染。儲油罐徑厚比通常超過1 000，加工制造和使用過程中不可避免地出現局部凹凸、軸線偏移、罐壁腐蝕等隨機幾何缺陷，可能嚴重影響其受力性能，從而導致抗震可靠度顯著降低[1]。現有規范沒有考慮儲油罐隨機初始幾何缺陷對結構受力性能的影響[2]。開展含隨機初始幾何缺陷的儲油罐的抗震性能及可靠性評價研究具有重要的理論意義和工程應用價值。

當前儲油罐幾何缺陷的模擬主要有一致缺陷模態法或隨機缺陷模態法[3]。一致缺陷模態法認為缺陷構型與一階屈曲模態一致時對結構受力產生的影響最不利[4]。然而，薄壁殼結構屈曲經常呈現多樣性，前幾階屈曲荷載有時十分接近，結構的最不利缺陷構型應該考慮前幾階屈曲模態的組合，即采用改進的一致缺陷模態法更為合理[5]。Maheri等[6]在假定儲油罐罐壁沿環向均勻腐蝕的基礎上，通過對具有不同腐蝕年限的儲油罐進行抗震分析，研究了腐蝕缺陷對儲油罐抗震性能的影響。楊宏康等[7]等基于壓力-位移格式的流固耦合模型建立等效動力擾動方程并引入地震動多維特性，通過求解動態Lyapunov特征指數確定儲液罐的動力失穩概率。

本文將初始幾何缺陷構型視為屈曲模態的線性組合，缺陷幅值作為隨機變量以便考慮隨機初始缺陷對儲液罐結構抗震可靠度的影響。基于附加質量法開發了用戶自定義單元以實現對儲油罐內液體晃動作用的模擬，采用增量動力分析法和Budiansky-Roth準則校核了地震作用下罐壁失穩臨界應力值。進而，考慮地震動和材料性能的隨機性，以儲油罐罐壁底部最大壓應力不超過罐壁許用應力為極限狀態，考察了隨機初始幾何缺陷對儲油罐結構抗震可靠度的影響。

1 儲油罐抗震分析的附加質量法

地震作用下，儲油罐內液體的晃動引起罐壁的變形，由于罐內液體晃動產生的動力作用是造成地震作用下儲油罐破壞的主要原因。假定罐壁為剛性，Housner等[8]將儲液罐內液體的動力效應分為液體隨罐體同步低頻運動產生的脈動分量和高頻晃動產生的對流分量兩部分。由于脈動分量和對流分量的頻率相差較大，不會出現耦合效應，通常可以分開考慮。其中，對流部分的壓力對儲油罐罐壁的影響較小，且可以通過添加防晃板來抑制，通常予以忽略[9-10]。基于此假定，附加質量法以附著于罐壁的等效質量考慮罐內液體運動脈動分量作用，同時忽略液體的其他作用。

1.1 附加質量法

本文采用Veletsos理論[11]求解動水壓力，假定罐內液體均質、無黏、不可壓縮，自由液面壓力與液體晃動之間呈線性分布，并忽略液體對流部分的影響。水平地震加速度作用下，脈沖壓力Pi(η,θ,t)沿罐壁豎向及環向的分布如圖1、圖2所示，其解可表示為

(1)

(2)

(3)

水平地震作用下，將脈沖壓力表示為加速度和質量的乘積可得罐壁任一點處的附加質量[12]，并采用集中質量矩陣表示單元的附加質量[13]。考慮到儲油罐有限元模型單元尺寸遠小于儲油罐的直徑，將每個單元的質量作簡化處理，集中到該單元的第一個節點處，單元中心與整體直角坐標系的夾角也由該節點對應的夾角代表。

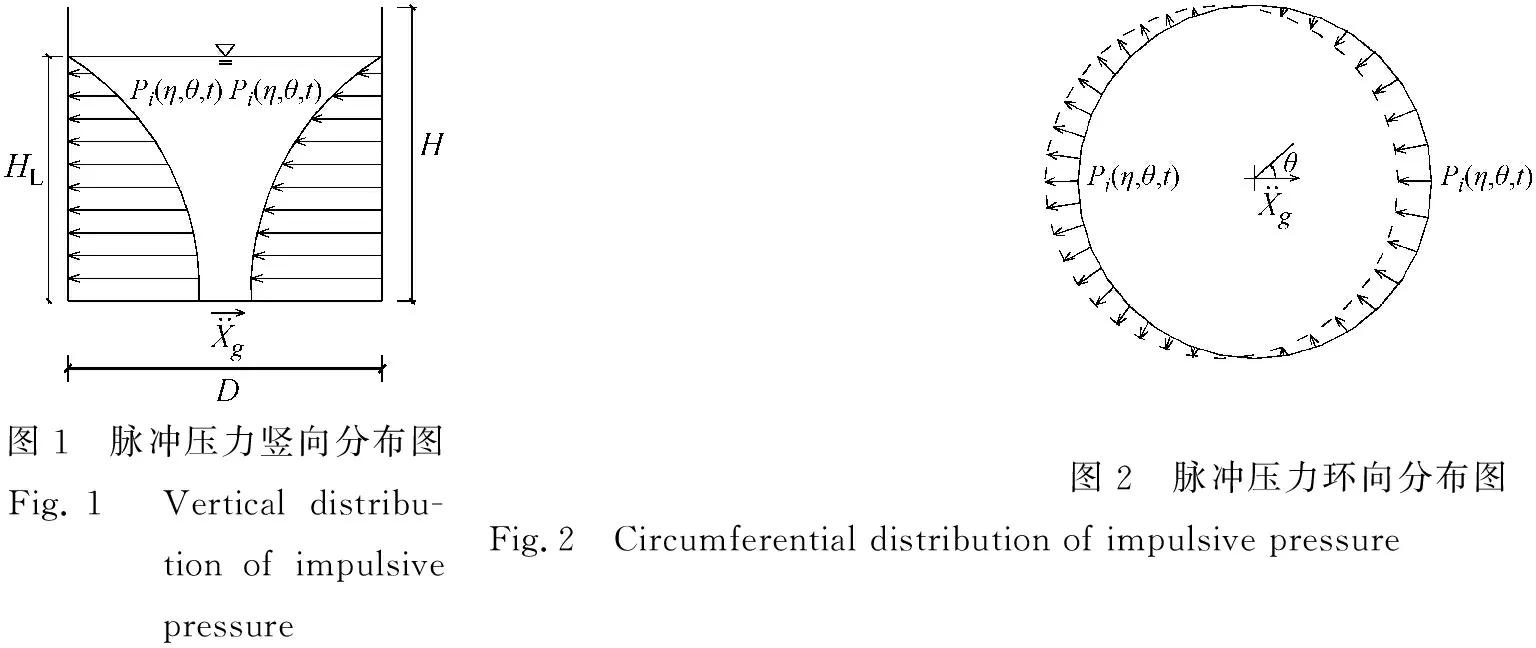
圖1 脈沖壓力豎向分布圖Fig.1 Vertical distribu-tion of impulsive pressure圖2 脈沖壓力環向分布圖Fig.2 Circumferential distribution of impulsive pressure

1.2 自定義單元開發及驗證

根據上述原理，基于ABAQUS用戶自定義單元UEL編寫子程序實現附加質量法[14]，其主要調用流程如圖3所示。

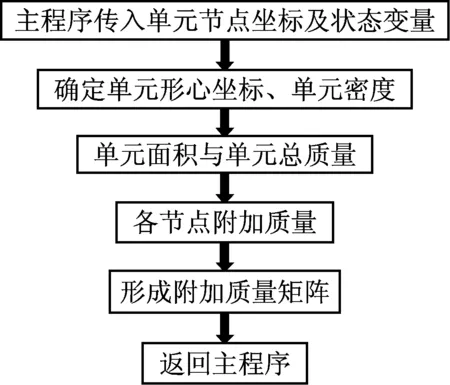
圖3 用戶子程序調用流程圖Fig.3 The flow chart for calling the user defined subroutine

為了驗證本文自定義子程序的正確性，采用附加質量用戶單元通過ABAQUS求解文獻[15]中儲油罐模型的自振周期及振型進行比較。具體包括：儲油罐振動模態、環向波數、自振周期。圖4為前5階奇數模態分析結果，儲油罐環向波數與自振周期的分布情況見圖5。

可以發現，采用本文附加質量法子程序求解的儲油罐模態及環向波數的整體分布與參考文獻[15]的結果一致，儲油罐自振周期隨著環向波數的增加先增大后減小，當環向波數為8時，周期達到最大值。所得前9階周期與文獻結果也接近(見表1)，驗證了本文附加質量法子程序的正確性。

2 地震作用下儲油罐失穩臨界應力分析

(a) 第1階模態俯視圖

(b) 第3階模態俯視圖

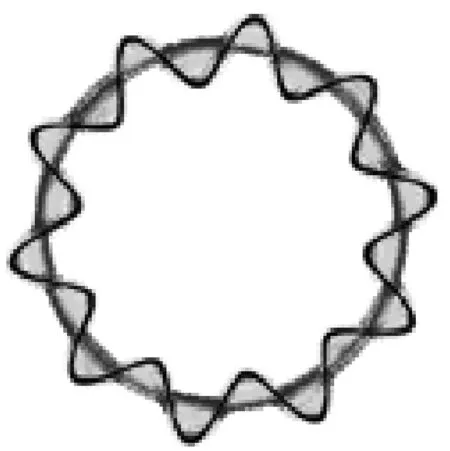
(c) 第5階模態俯視圖圖4 儲液罐模態圖Fig.4 Vibration modes of the storage tank

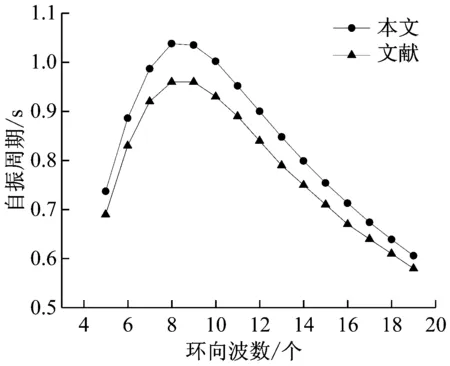
圖5 環向波數與自振周期圖Fig.5 The natural vibration period and number of circumferential waves

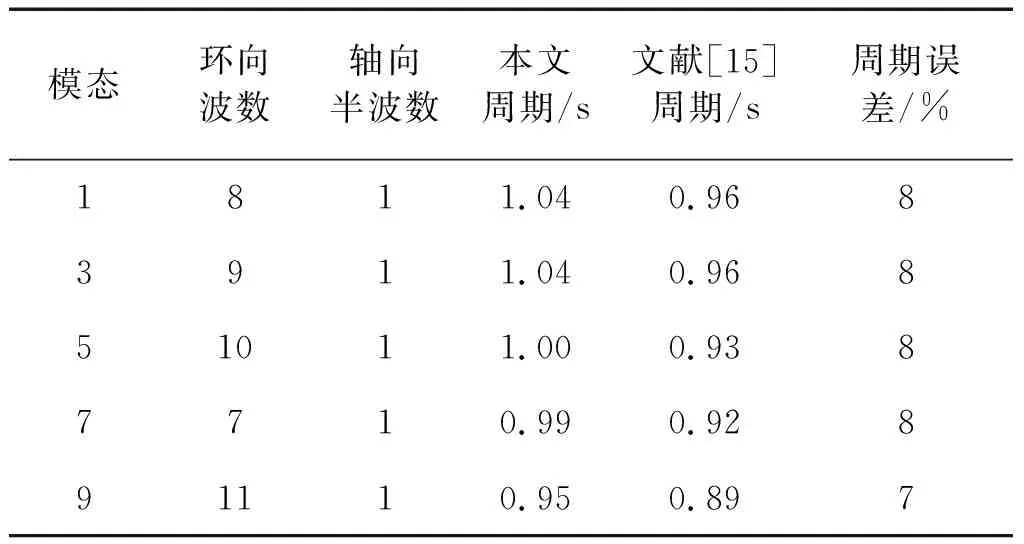
表1 本文附加質量法計算的儲油罐自振周期與文獻[15]比較Tab.1 Comparison of the natural period of the oil tank solved by present added mass method with reference [15]

一般認為，軸向壓應力與環向應力是導致圓柱形立式儲油罐罐壁屈曲的基本原因。本文采用《立式圓柱形鋼制焊接油罐設計規范》(GB 50341—2014)給出的罐壁失穩準則進行后續可靠度分析，即

σ1≤[σcr]

(4)

式中:σ1為罐壁底部最大軸向壓應力,MPa；[σcr]為底圈罐壁許用臨界應力。為了驗證規范給定儲液罐罐壁失穩準則的合理性和適用性，此處采用Budiansky-Roth準則[16]通過增量動力分析法確定給定地震動下儲液罐罐壁失穩時的應力狀態。即：隨著地震動幅值的增大儲油罐結構處于臨界失穩狀態，加速度峰值的繼續增加會使得儲油罐變形發生突然增大，此時對應的罐壁最大壓應力即為臨界應力。基于本節儲油罐有限元模型，分別輸入El Centro波、遷安波以及San Fernando波進行罐壁失穩臨界應力分析。

2.1 模型概況

罐壁采用Q345鋼材，材料本構選用混合隨動強化模型，具體參數如表2所示[17-18]。根據截面慣性矩等效原則，對抗風圈進行簡化后儲油罐模型尺寸及有限元模型如圖6所示。彈塑性時程分析時采用瑞利阻尼，阻尼比為2%。

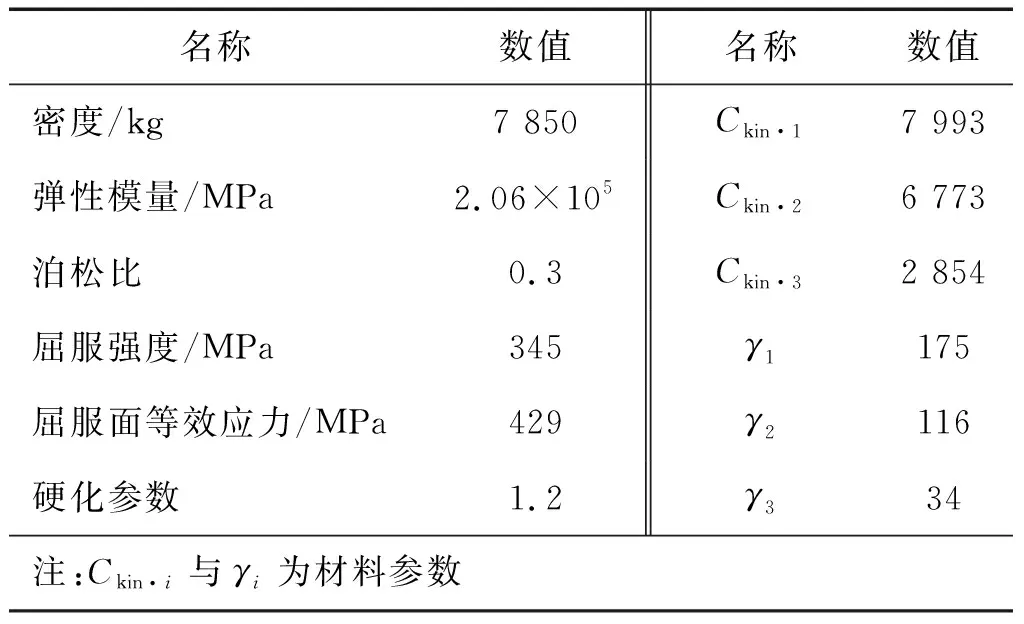
表2 鋼材本構模型參數Tab.2 Parameters of the constitutive law of steel

(a) 儲油罐幾何尺寸

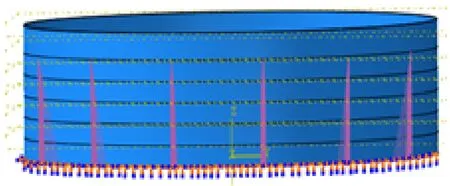
(b) 儲油罐有限元模型圖圖6 儲油罐幾何尺寸及有限元模型Fig.6 The geometry sizes and finite element model of the oil storage tank

2.2 罐壁失穩臨界應力

為了合理地確定儲油罐抗震可靠度分析過程中罐壁失穩時的臨界應力，考慮場地條件并結合儲油罐自振特性，結合抗震規范[19]中的選波規定，選取El Centro波、遷安波以及San Fernando波進行分析。三條波的加速度時程記錄如圖7所示。

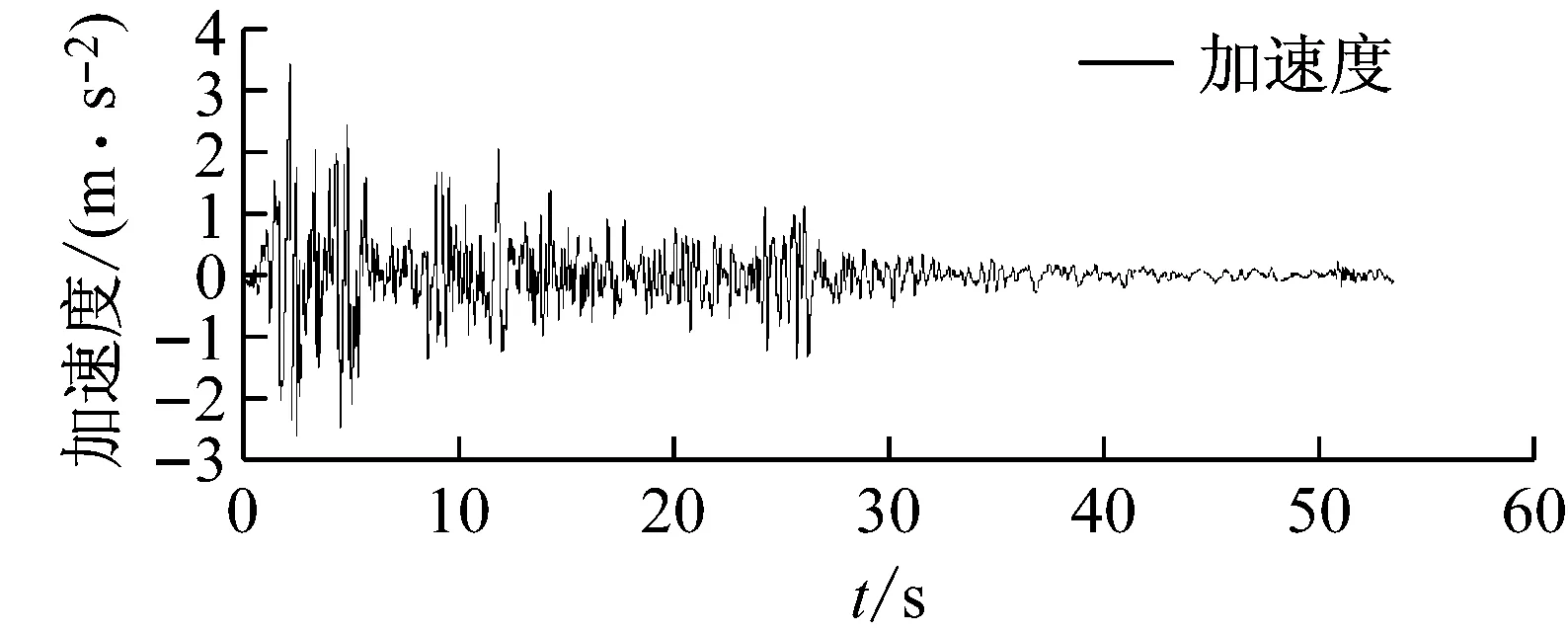
(a) EL Centro波

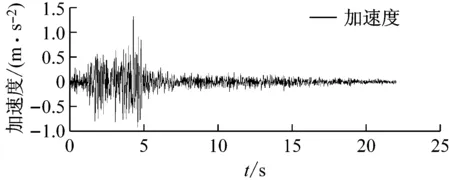
(b) 遷安波

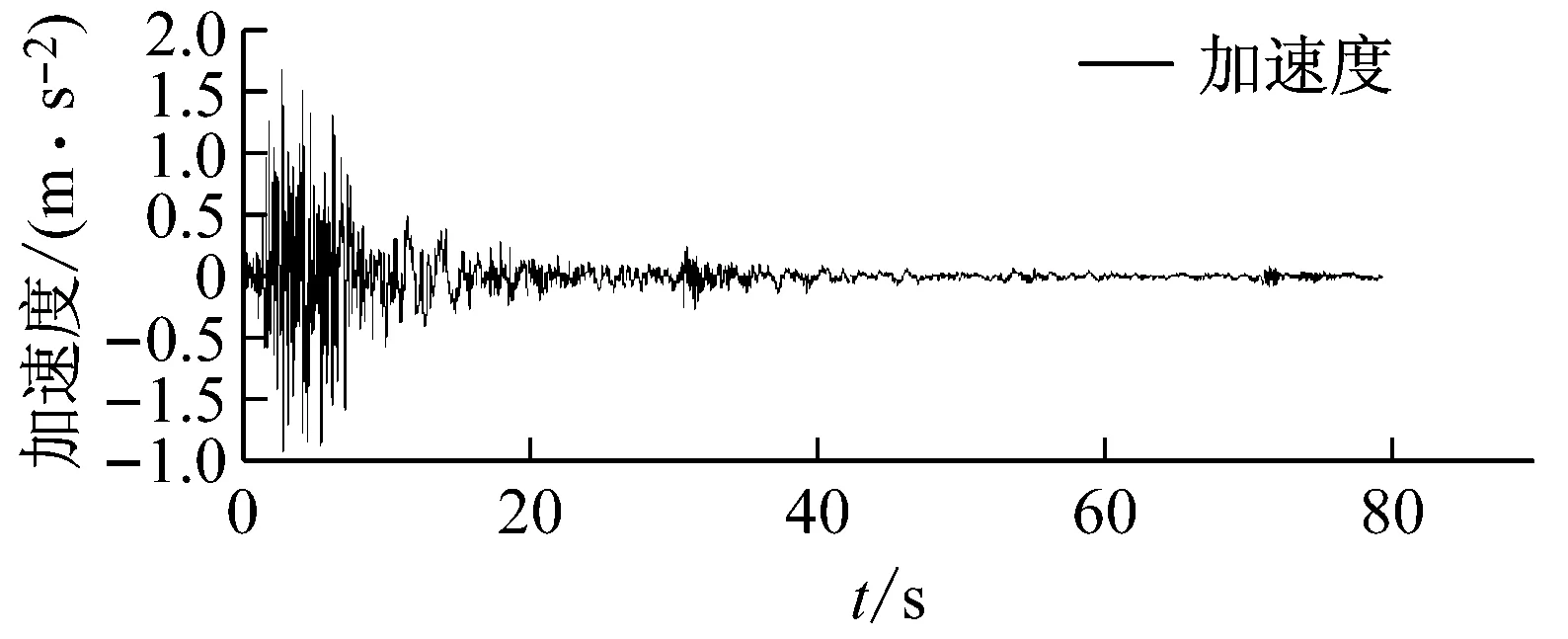
(c) San Fernando波圖7 地震波加速度時程曲線Fig.7 Time histories of the ground motions

基于所選地震波對2.1節中給出的儲油罐進行彈塑性增量動力分析，得到加速度峰值為0.1～0.65g時儲油罐節點位移和應力狀態。不同加速度峰值的地震波作用下儲油罐最危險點節點處罐壁徑向位移時程曲線如圖8所示。為更加清晰顯示最大徑向位移時程曲線的跳躍情況，此處沒有給出El Centro波和San Fernando波作用下所有的儲油罐最大徑向位移時程。可以發現，不同峰值遷安波作用下，儲油罐罐壁最大徑向位移增大幅度均勻，罐壁受力始終處于彈性階段。El Centro波作用下，加速度峰值為0.1～0.2g時，儲油罐最大徑向位移增大幅度均勻，儲油罐處于彈性變形。當加速度峰值達到0.25g時，儲油罐最大徑向位移曲線較加速度峰值為0.2g時明顯突變，結構進入塑性階段。類似地，San Fernando波作用下，加速度峰值為0.1～0.3g時，儲油罐最大徑向位移的變化穩定，儲油罐變形處于彈性階段。當加速度峰值達到0.35g時，最大徑向位移時程較加速度峰值為0.3g時發生明顯跳躍。

為了更好地考察儲液罐結構的變形狀態，將加速度峰值與對應的儲油罐最大徑向位移之間的關系示于圖9。可以發現，儲油罐在El Centro波作用下最容易發生破壞，儲油罐臨界加速度為0.245g，對應的儲油罐底部最大軸向壓應力值為23.33 MPa，與規范GB 50341的計算值22.3 MPa十分接近。因此，后續可靠度分析中取罐壁臨界屈曲壓應力為22.3 MPa。

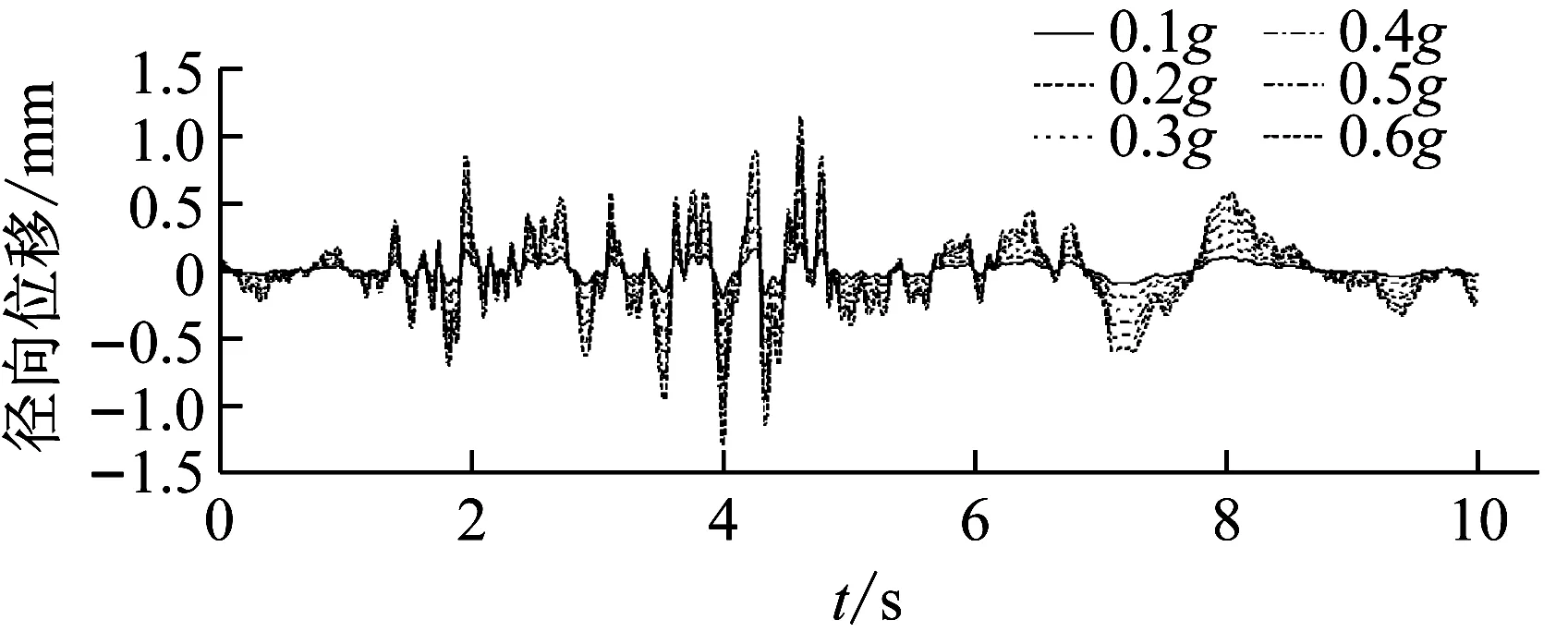
(a) 遷安波

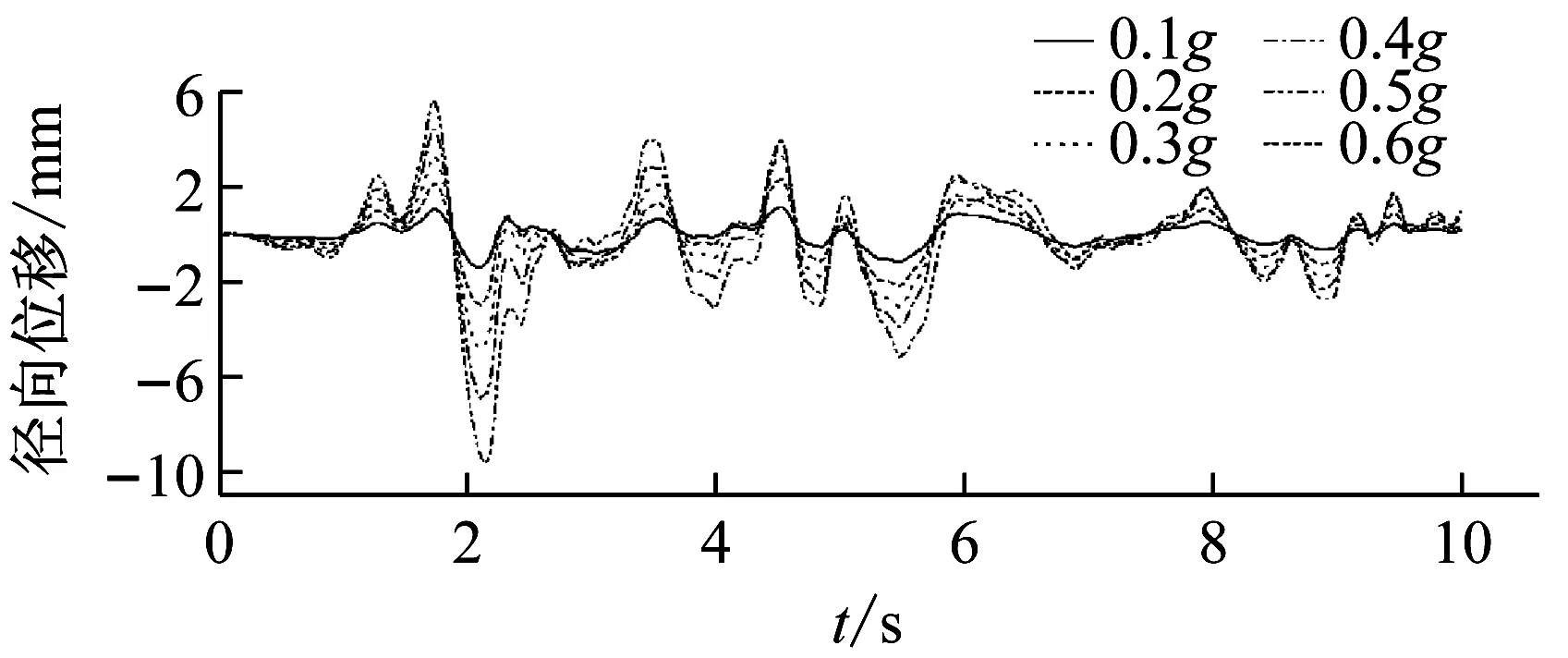
(b) El Centro波

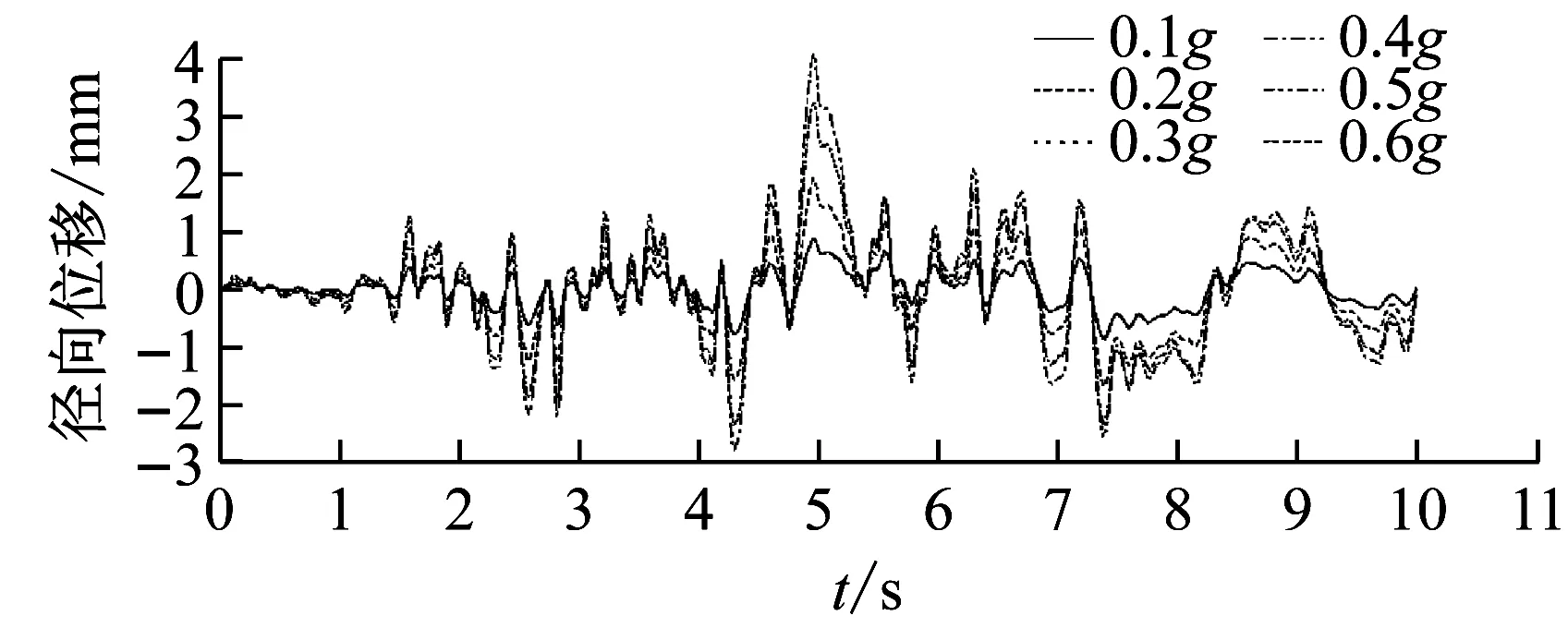
(c) San Fernando波圖8 不同加速度峰值地震作用下徑向位移時程曲線Fig.8 The radial displacement time histories under different PGAs

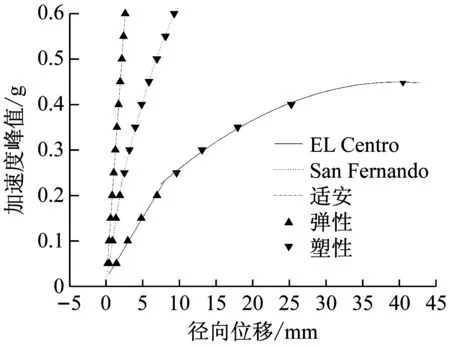
圖9 最大徑向位移-峰值加速度曲線Fig.9 Maximum radial displacement versus peak ground acceleration (PGA)

3 考慮缺陷影響的儲油罐抗震可靠度分析

3.1 隨機因素

3.1.1 隨機地震動

根據《建筑抗震設計規范》(GB 50011—2010)關于時程分析法所用地震加速度峰值的規定，采用劉章軍等建議的譜表示-隨機函數法，生成抗震設防烈度為7度和8度的非平穩地震動樣本，代表性加速度樣本如圖10所示。限于篇幅，更多關于譜表示-隨機函數法及相關參數的取值參見文獻[20]。

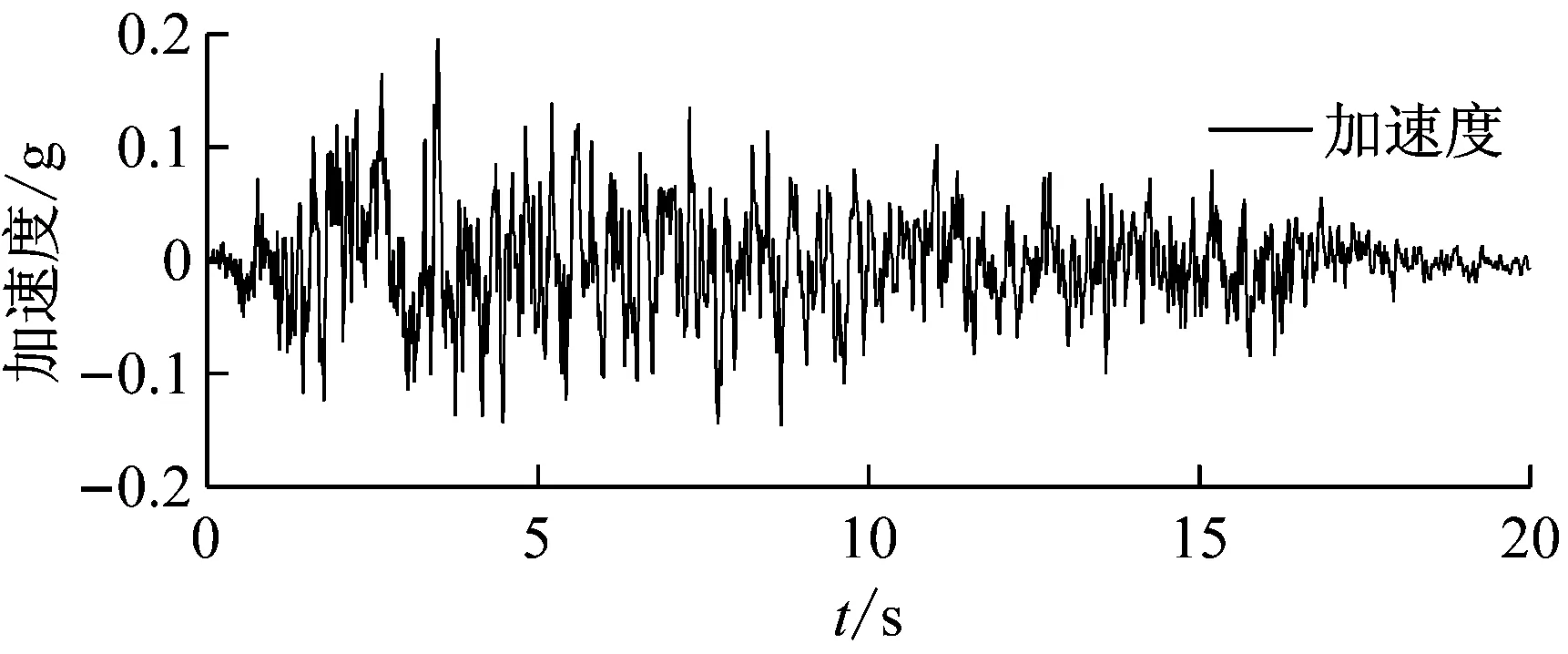
圖10 代表性樣本時程曲線圖Fig.10 Time history of a ground motion sample

3.1.2 隨機幾何缺陷

分析結果表明，儲油罐模型前5階屈曲特征值十分接近，最大差別小于5%，呈現多低階屈曲模態特征。采用第1、第3、第5階屈曲模態的線性組合模擬幾何缺陷構型。以規范規定的最大施工誤差為缺陷幅值，假定缺陷幅值服從均值為0、標準差為0.004 6的正態分布，采用拉丁超立方抽樣方法生成233個初始幾何缺陷樣本。

3.1.3 材料隨機性

鋼材強度及彈性模量采用正態分布模型，均值及變異系數如表3所示。

表3 材料性能參數的均值與變異系數Tab.3 Mean and coefficient of variation of steel

3.2 儲油罐抗震可靠度分析

采用第2節給出的儲液罐有限元模型，基于3.1.1生成的地震動樣本開展彈塑性動力時程分析。通過Matlab編程批量生成考慮隨機初始幾何缺陷的儲油罐有限元命令流進行求解，概率密度函數由Ksdensity函數求得。由圖11和圖12可知，7度隨機地震作用下，不含隨機初始幾何缺陷的儲油罐底部最大軸向壓應力分布于2～13.5 MPa，概率密度函數的偏度系數bx、峰度系數bk分別為0.3和4.33，接近于正態分布。考慮隨機初始幾何缺陷后，儲油罐底部最大軸向壓應力分布范圍為3.5～36 MPa，明顯較不考慮幾何缺陷時擴大。同時，隨機初始幾何缺陷的存在使得儲油罐抗震可靠度由原來接近于1降為91.5%。

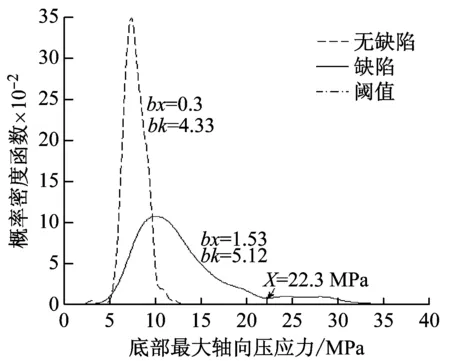
圖11 7度隨機地震作用下儲油罐底部最大軸向壓應力概率密度函數Fig.11 Probability density functions of the maximum axial compressive stress at bottom of the storage tank under stochastic ground motions for 7 degree fortification

圖12 7度隨機地震作用下儲油罐底部最大軸向壓應力概率分布函數Fig.12 Cumulative distribution functions of the maximum axial compressive stress at bottom of the storage tank under stochastic ground motions for 7 degree fortification

8度隨機地震作用下，儲油罐底部最大軸向壓應力的概率密度函數及累積概率分布函數分別見圖13和圖14所示。考慮隨機初始幾何缺陷后，儲油罐底部最大軸向壓應力的分布范圍由9～25 MPa變為4～63 MPa，離散性明顯增大，抗震可靠度由99.99%降低為50.25%。

圖13 8度隨機地震作用下儲油罐底部最大軸向壓應力概率密度函數Fig.13 Probability density functions of the maximum axial compressive stress at bottom of the storage tank under stochastic ground motions for 8 degree fortification

由圖11和圖13還可以發現，不考慮隨機初始幾何缺陷情況下，儲油罐底部最大軸向壓應力近似服從正態分布，而考慮隨機初始缺陷后其概率分布明顯偏離正態分布。此外，隨著設防烈度的提高，罐壁底部最大軸向壓應力離散性增大，相同隨機初始幾何缺陷下，地震作用的增大使得儲油罐的抗震可靠度顯著降低。

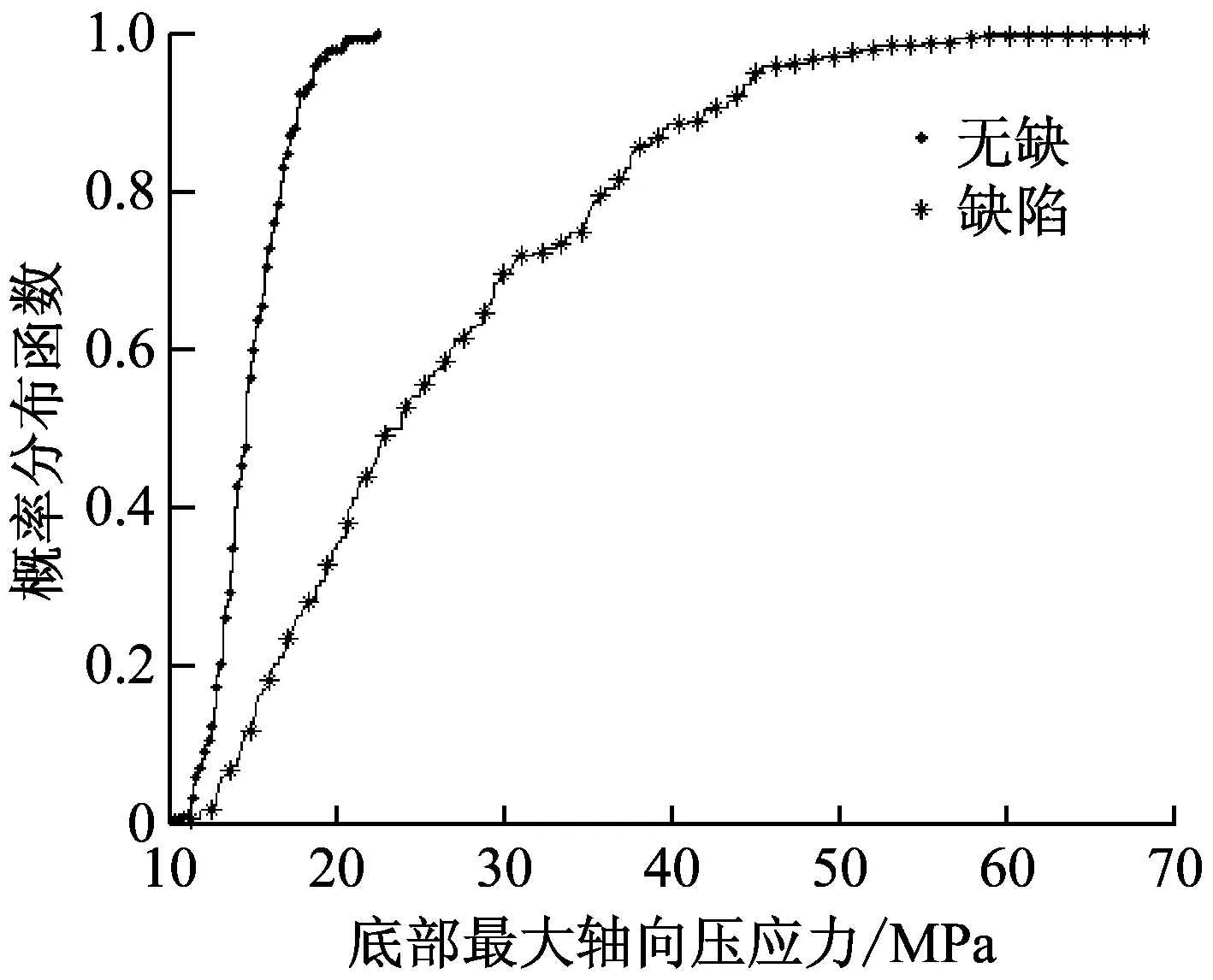
圖14 8度隨機地震作用下儲油罐底部最大軸向壓應力概率分布函數Fig.14 Cumulative distribution functions of the maximum axial compressive stress at bottom of the storage tank under stochastic ground motions for 8 degree fortification

4 結 論

將缺陷構型視為屈曲模態的線性組合，按照規范施工誤差限值將缺陷幅值處理為零均值正態隨機變量，從而考察了隨機缺陷對儲油罐結構抗震可靠度的影響。其中，基于ABAQUS用戶自定義單元開發了附加質量子程序用以考慮罐內流體的晃動效應。進而，在7度和8度隨機地震作用下，對比分析了考慮幾何缺陷影響與未考慮缺陷影響儲油罐抗震可靠度。結論如下：

(1)考慮罐壁單元形狀的任意性，通過ABAQUS的UEL用戶自定義單元開發，實現了基于附加質量法的缺陷儲油罐抗震性能彈塑性時程分析。

(2)采用Budiansky-Roth準則，通過增量動力分析法計算了在給定地震動作用下儲液罐罐壁失穩時的臨界應力，與規范罐壁失穩臨界應力公式計算值吻合。

(3)相同隨機地震作用下，考慮隨機初始幾何缺陷后，儲油罐底部最大軸向壓應力分布的離散性明顯增大，其概率分布偏離正態分布。

(4)算例結果表明，7度隨機地震作用下，考慮隨機初始幾何缺陷使得儲油罐抗震可靠度由1降為91.5%；8度隨機地震作用下，隨機初始幾何缺陷導致儲油罐抗震可靠度由99.99%大幅降低為50.25%。