基于修正壓力場理論的活性粉末混凝土梁抗剪分析

王 強， 金 凌 志*， 蔣 春 松

( 1.桂林理工大學 土木與建筑工程學院， 廣西 桂林 541004；2.桂林理工大學 廣西巖土力學與工程重點實驗室， 廣西 桂林 541004 )

0 引 言

普通的鋼筋混凝土梁的抗剪問題十分復雜，國內外規范中的抗剪承載力計算方法大多為半理論半經驗公式，力學模型不明確，基本以試驗數據回歸得到．且出于對工程安全的考慮，其計算結果一般都比較保守．20世紀初Ritter與M?rsch提出了經典45°桁架模型，以力學為基礎的計算方法逐漸得到認可，并不斷發展完善，其中以20世紀80年代加拿大學者Vecchio和Collins[1-2]提出的修正壓力場理論(MCFT)較為經典，并成為《加拿大橋梁結構設計規范》[3]、《加拿大混凝土結構設計規范》[4]和《美國橋梁結構設計規范》[5]中抗剪計算方法的理論基礎．該理論忽略縱筋的消栓作用，將裂后混凝土仍看成連續性材料，應力和應變都取平均值，同時滿足莫爾圓定理．依據混凝土和鋼筋微元體單元在整個受荷過程都需滿足假定的本構關系、相容方程和應力平衡條件，考慮裂縫間混凝土骨料的咬合力和摩擦力，給出鋼筋混凝土構件在純剪作用下的模型公式，若疊加彎矩作用，則可得到其在彎剪共同作用下的計算模型[6-7]．該模型未忽略開裂后混凝土的拉應力，故鋼筋混凝土構件的非線性性能即全階段荷載-變形特征能被準確描述．

活性粉末混凝土(reactive powder concrete，RPC)是法國Bouygues試驗室在20世紀90年代研制出的一種具有超高強度、高韌性、高耐久性的新型水泥基復合材料[8]，且在材料特性方面已有較多研究[9-11]．2015年《活性粉末混凝土》(GB/T 31387—2015)[12]頒布，對RPC各組分的配合比、制備技術、養護條件、強度等級的劃分與測試方法等進行了統一規定，標志著RPC工程應用時代的到來，所以相關結構設計規范也理應被提上日程．RPC的強度較高，若受力縱筋仍采用現行工程中主推的HRB400級鋼筋，對于非預應力構件則會出現配筋率過高的情況，對施工造成不便，故用高強度鋼筋與RPC組成的結構構件近年來受到更多的關注[13-14]．鑒于此，本文采用的主受力筋為HRB500級鋼筋．

文獻表明[15-17]，配筋RPC構件的研究主要以試驗為主，而相應深入的理論模型分析較少．本文在Vecchio和Collins提出的MCFT(混凝土板受純剪)基礎上，疊加彎矩效應，結合RPC材料特點，建立在彎剪復合作用下配筋RPC梁截面受荷全過程分析模型，并將分析結果與試驗結果進行對比．

1 模型的建立

1.1 平衡方程和相容條件

(1)基本假定

如圖1所示，平面鋼筋單元和RPC單元共同承擔開裂鋼筋RPC單元的外力，假定鋼筋只能承擔拉力和壓力，忽略其抗剪作用，則

fx=fcx+ρsxfsx

(1)

fy=fcy+ρsyfsy

(2)

vsxy=0

(3)

vxy=vcxy+vsxy=vcxy=v

(4)

式中：ρsx和ρsy分別為鋼筋單元x向和y向配筋率；fcx和fcy分別為RPC單元x向和y向正應力；fsx和fsy分別為鋼筋單元x向和y向正應力；fx和fy分別為鋼筋RPC單元x向和y向正應力；vxy、vcxy和vsxy分別為鋼筋RPC單元、RPC單元和鋼筋單元的剪應力．

圖1 鋼筋RPC平面應力單元

(2)相容方程(開裂鋼筋RPC單元)

如圖2(a)所示，ε1和ε2分別為穿越幾條斜裂縫的平均主拉應變和主壓應變，裂縫傾角為θ，假定RPC和鋼筋之間無滑移，即如圖2(b)所示，單元整體應變符合莫爾圓理論，則

(5)

由三角形2Ax和2By的幾何關系可得：

γxy=2(εx-ε2)cotθ

(6)

γxy=2(εy-ε2)tanθ

(7)

由式(5)～(7)可得：

(8)

(9)

式中：εx和εy分別為鋼筋RPC單元x向和y向應變，γxy為其剪應變．

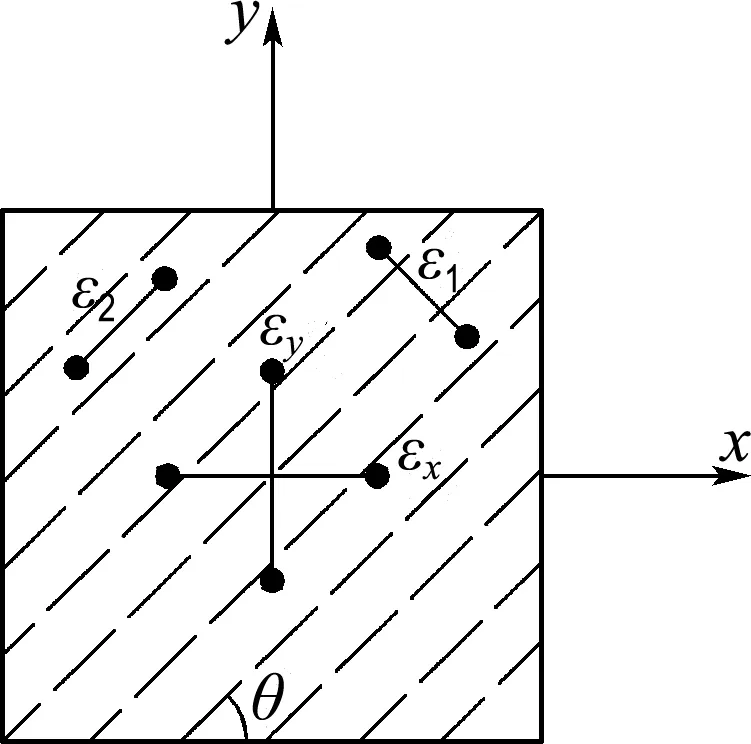
(a) 單元平均應變(開裂后)

(3)開裂RPC單元應力平衡條件

假定開裂后RPC單元主應變與主應力的傾角方向相同，大小均為θ，見圖3，則

fc2=-fc1+v(tanθ+cotθ)

(10)

其中fc1和fc2分別為開裂后RPC單元的主拉應力和主壓應力．

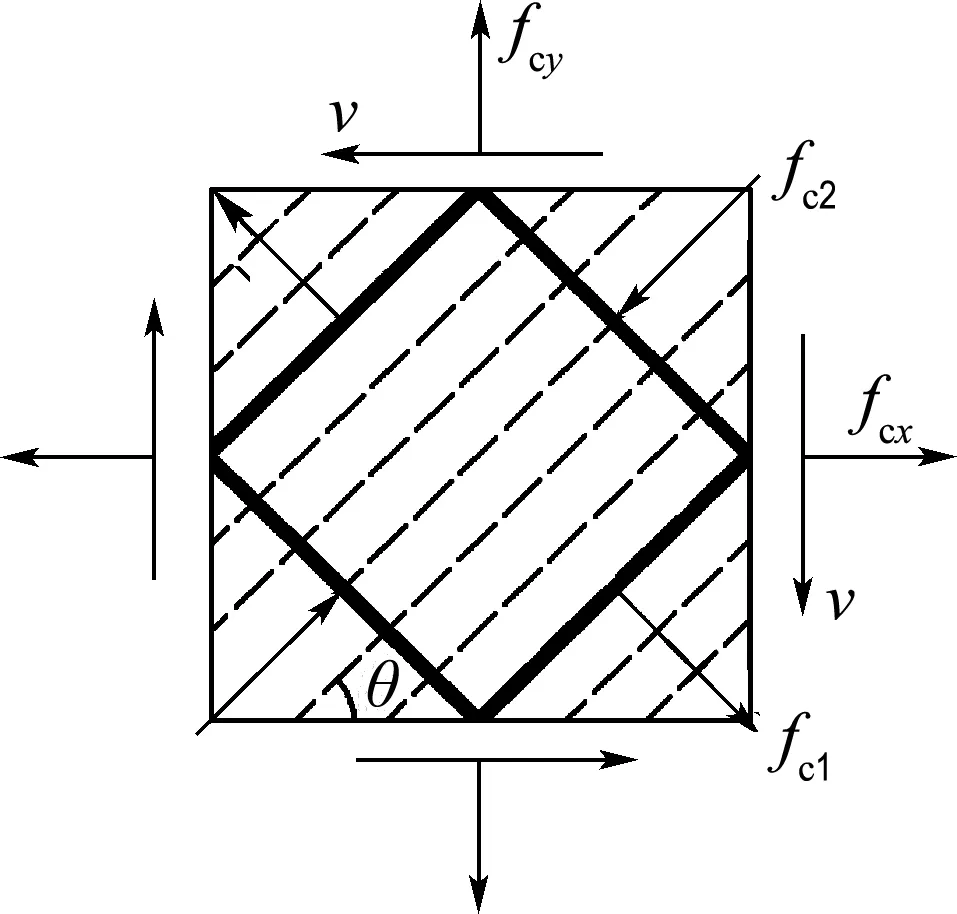
(a) RPC單元主應力(開裂后)

1.2 材料的應力應變關系

(1)鋼筋

鋼筋的本構關系采用雙直線模型，即

當εs≤εyv時(上升段)，有

fsy=εsEs

(11)

當εyv<εs≤εsu時(水平段)，有

fsy=fyv

(12)

式中：εyv為箍筋的屈服應變，Es為鋼筋的彈性模量，εsu為鋼筋的極限拉應變，fyv為箍筋的屈服強度．

(2)RPC

①RPC受拉應力應變關系．文獻[18]給出了RPC軸拉σ-ε曲線，但未給出具體模型，其形狀與文獻[19-20]中鋼纖維混凝土材料的受拉本構模型(見圖4(a))相似，故可近似采用，其公式為

當ε1≤εcr時(上升段)，有

(13)

當ε1>εcr時(下降段)，有

(14)

(15)

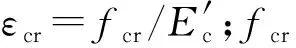
(a) 受拉本構關系

②RPC受壓應力應變關系．普通混凝土材料在受到拉壓二維應力共同作用時，其極限抗壓強度比只受一維壓應力時的極限抗壓強度低的現象被稱為軟化現象，RPC也存在該現象．彎剪復合應力下的RPC單元也是處在拉壓二維應力的共同作用下，故單元的主壓應力不僅與主壓應變有關，與主拉應變也有很大關系．為考慮RPC材料的軟化現象，也可用文獻[20]中鋼纖維混凝土的受壓本構模型來代替，如圖4(b)所示，其公式為

(16)

(17)

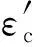
1.3 梁在純剪下的應力分析

(1)應力平衡(裂縫之間)

(18)

其中V為截面受到的剪力．由圖5(c)箍筋方向力的平衡可得

fsyAsy=(fc2sin2θ-fc1cos2θ)bs

(19)

由式(10)、(18)、(19)可得

(20)

當RPC達到極限抗拉強度(fc1=ft)以及箍筋屈服(fsy=fyv)時，式(20)即為梁在純剪下的承載力表達式．同時可求出梁在純剪作用下所受剪力的水平分量Nv的表達式為

Nv=bdv(fc2cos2θ-fc1sin2θ)=Vcotθ-fc1bdv

(21)

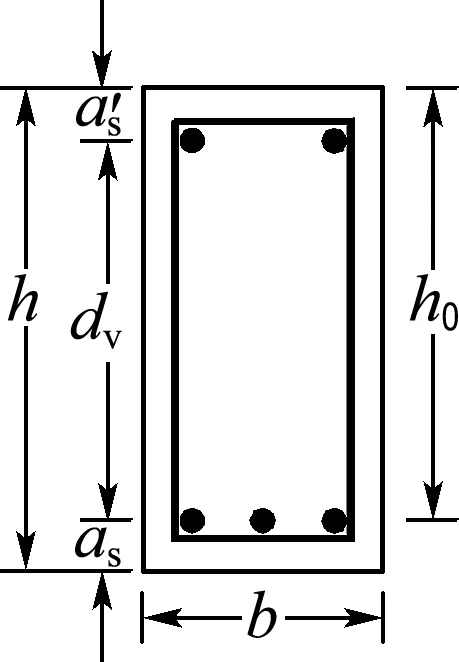
(a) 截面參數

F(c) 箍筋的力

圖5 純剪下梁的應力

Fig.5 Stress of beams under pure shear

(2)跨越裂縫的力的平衡

MCFT的基本假定將斜裂縫處混凝土面理想化為光滑平面，但實際情況是會存在裂縫處界面上的骨料咬合作用．RPC中雖無粗骨料，但含有鋼纖維，所以開裂后界面上雖不存在骨料咬合力，但會出現鋼纖維的抗拔阻力．且當外荷載較大，箍筋屈服后應力保持穩定時，RPC在裂縫處的拉應力已基本只剩余鋼纖維的抗拔阻力，1-1截面(裂縫間)和2-2截面(裂縫處)兩處的應力應相等，如圖6所示，由豎向力的平衡可得

(22)

式中：fsycy為箍筋的拉應力，當fsycy=fyv，即箍筋屈服時，fc1達到極限值fc1max，則

(23)

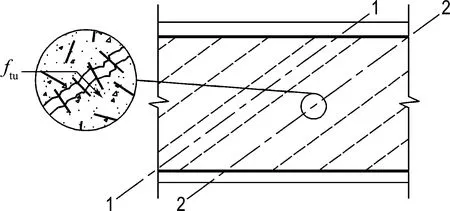
(a) 裂縫處鋼纖維的抗拔阻力

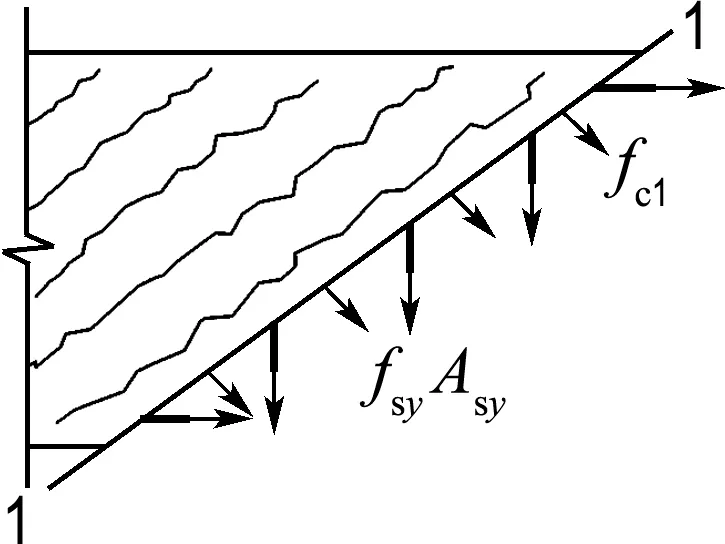
(b) 裂縫間平均應力

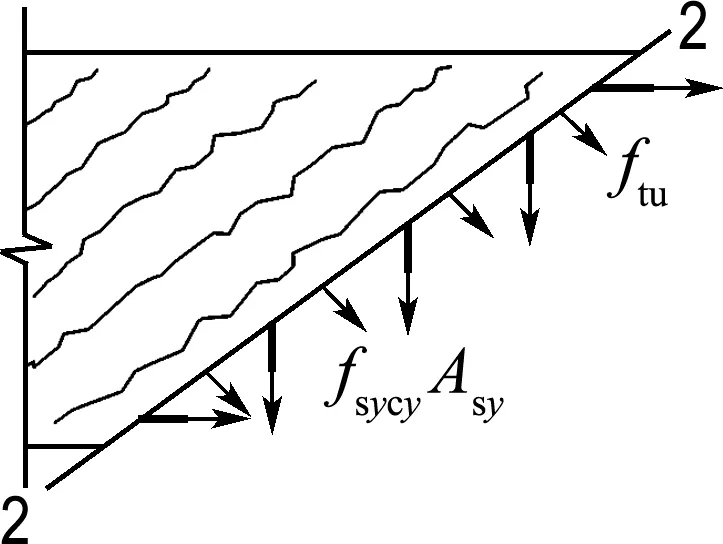
(c) 裂縫處局部應力

圖6 RPC的應力分布

Fig.6Stress distribution of RPC

1.4 梁在純彎矩作用下的受力分析

圖7為純彎矩作用下構件截面應變與應力簡化圖形，符合平截面假定．由于截面開裂后RPC中存在鋼纖維的抗拔阻力，故不能忽略RPC的拉應力，參考文獻[19]的分析方法，用集中力的方式將截面應力全部簡化，見圖7(e)．

將梁截面壓應力的曲線圖形轉化為等效矩形，再轉化為集中力Nc，則

(24)

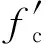
(25)

(26)

式中：εtop為梁頂受壓邊緣最大壓應變．將中和軸下RPC拉應力曲線圖形轉化為等效三角形，再轉化為拉力Tc，則

Tc=0.5ftbb(h-xc)

(27)

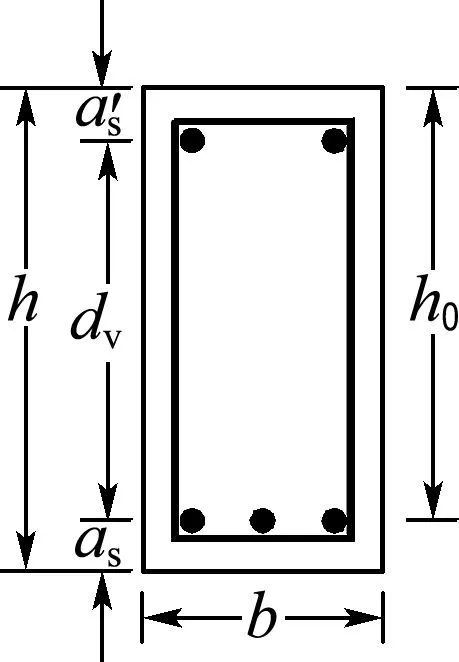
(a) 截面尺寸

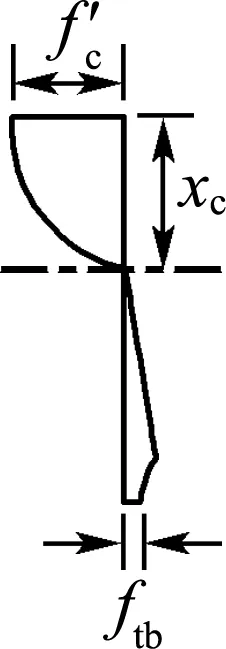
(c) RPC真實應力

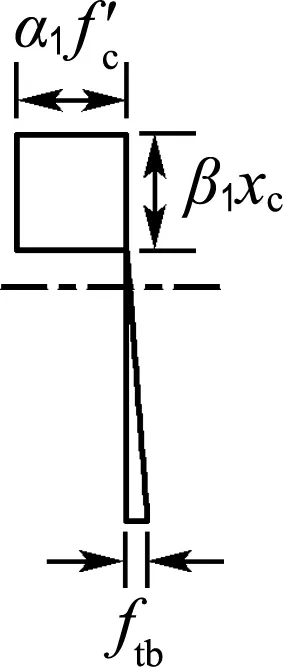
(d) 簡化應力

(e) 簡化為集中力

圖7 純彎矩下的應力應變

Fig.7 Stress and strain under pure bending moment

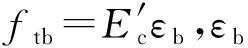
Ts=EsεsAs

(28)

(29)

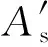
(30)

(31)

(32)

(33)

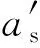
(34)

截面合力Np為

(35)

1.5 彎剪共同作用下的截面分析

1.5.1 分析假定

(1)將彎剪共同作用下梁截面的剪應力圖形的拋物線型簡化為均布力，則εx沿截面也為均勻分布．

(2)彎剪共同作用下梁截面仍符合平截面假定．如圖7(b)所示，在確定xc時疊加了剪切變形的影響，由于在純剪作用下εx的存在，xc減小，且隨著εx的增大而減小，若材料為均質彈性體，梁截面中點的應變值就是彎剪組合作用下的εx．

1.5.2 計算步驟

(1)確定截面幾何尺寸及材料強度．

(2)給定初始的ε1值．

(3)給定初始的θ值．

(4)給定初始的fsy值．

(5)由式(23)計算fc1max，再結合式(13)～(15)計算fc1．當ε1≤εcr時，fc1取式(13)的計算結果；當ε1>εcr時，fc1取式(14)和(23)結果的較小值．

(6)由式(20)計算V．

(7)由式(10)和(18)計算fc2．

(8)由式(17)計算fc2max，判斷fc2是否小于等于fc2max，是則繼續下一步，否則說明RPC達到極限抗壓強度，退出計算．

(9)由式(16)、(8)和(9)分別求ε2、εx和εy．

(10)由式(11)、(12)求fsy，并與第4步中給定的fsy值比較，若相等則繼續下一步，否則重回第4步，調整所給fsy的值，直至相等．

(11)由第6步計算的V以及公式M0=Va計算M0．

(12)給定一個初始的εtop，由式(25)和(26)求α1β1和β1．

(14)由式(34)以及式(24)、(27)和(29)聯合求解M，并驗算M與M0是否相等，是則繼續下一步，否則回到第12步，調整εtop直到滿足為止．

(15)由式(21)計算Nv，由式(35)以及式(24)、(27)、(28)和(29)聯合求解Np，驗算Np是否等于Nv，相等則輸出此時所需的變量，否則返回第3步調整θ直至滿足．

(16)記錄下此時數值然后返回第2步，增大ε1，進入下一個循環．

2 試驗概況

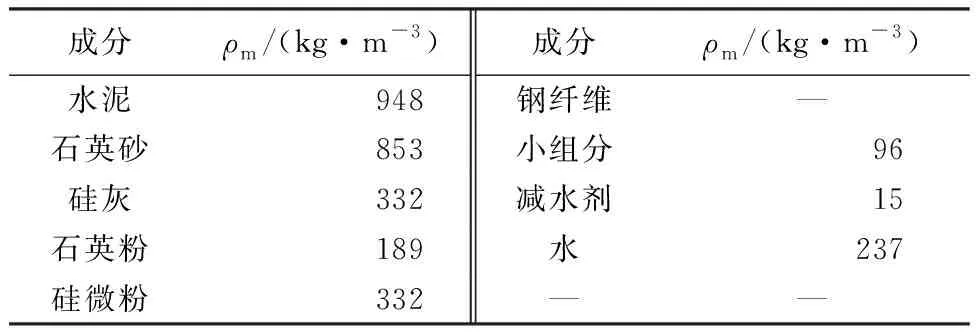
表1 RPC配合比

表2 RPC力學性能

表3 鋼筋力學性能

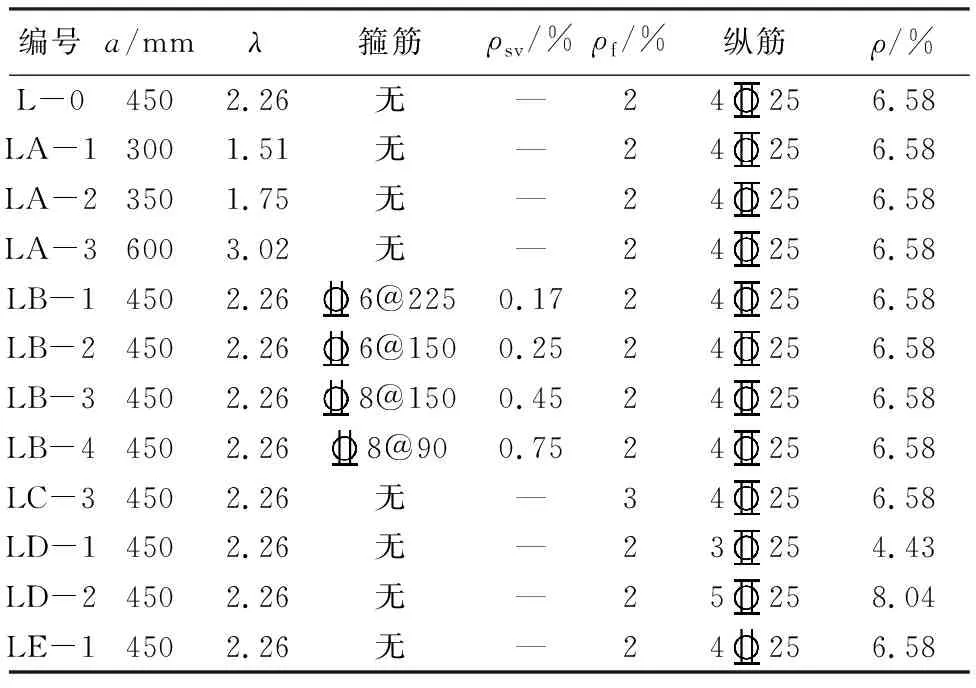
表4 試件參數

圖8 試驗方案及加載方式

3 結果分析

3.1 梁端剪力-箍筋平均應變關系

箍筋應變取加權平均值，其目的是消除加載點與支座處箍筋應變的影響，輸出計算模型中各級梁端剪力對應的箍筋應變，試驗梁在整個加載過程中箍筋應變實測值與理論計算值的對比見圖9．

由圖可得，計算值與實測值吻合較好，均能體現出隨著荷載的增加，箍筋應變隨梁端剪力的非線性增長趨勢，并且還能體現隨著配箍率的增加，箍筋應變隨梁端剪力增長放緩的趨勢．

3.2 梁端剪力-RPC主拉應力關系

基于B組試驗梁數據，輸出各級梁端剪力所對應的RPC主拉應力數值，其變化規律見圖10．

將圖10與RPC受拉本構關系以及文獻[16]中的試驗現象描述進行對比分析可得出以下結論：

(1)試驗梁的開裂機理為RPC主拉應力達到材料的極限抗拉強度，開裂荷載主要與RPC的極限抗拉強度有關，且隨著材料抗拉強度的增大而增大．

(2)截面出現斜裂縫后，由于RPC中存在鋼纖維的抗拔阻力，開裂截面的拉應力仍能保持較高的強度，從而使得構件具有較好的延性與韌性．

(3)箍筋可以起到延緩裂縫開展的作用，隨著配箍率的提高，RPC的殘余主拉應力，即鋼纖維的抗拔阻力下降速度變慢，直到構件快破壞時，其下降速度才變快．

3.3 極限承載力分析

將MCFT的計算結果與實測值進行比較，見表5．其中，Vcu為MCFT的計算結果，Vex為抗剪承載力實測值，公式中材料強度均取實測值．

由表5可以看出，MCFT計算值與實測值吻合良好，但也存在如下問題：

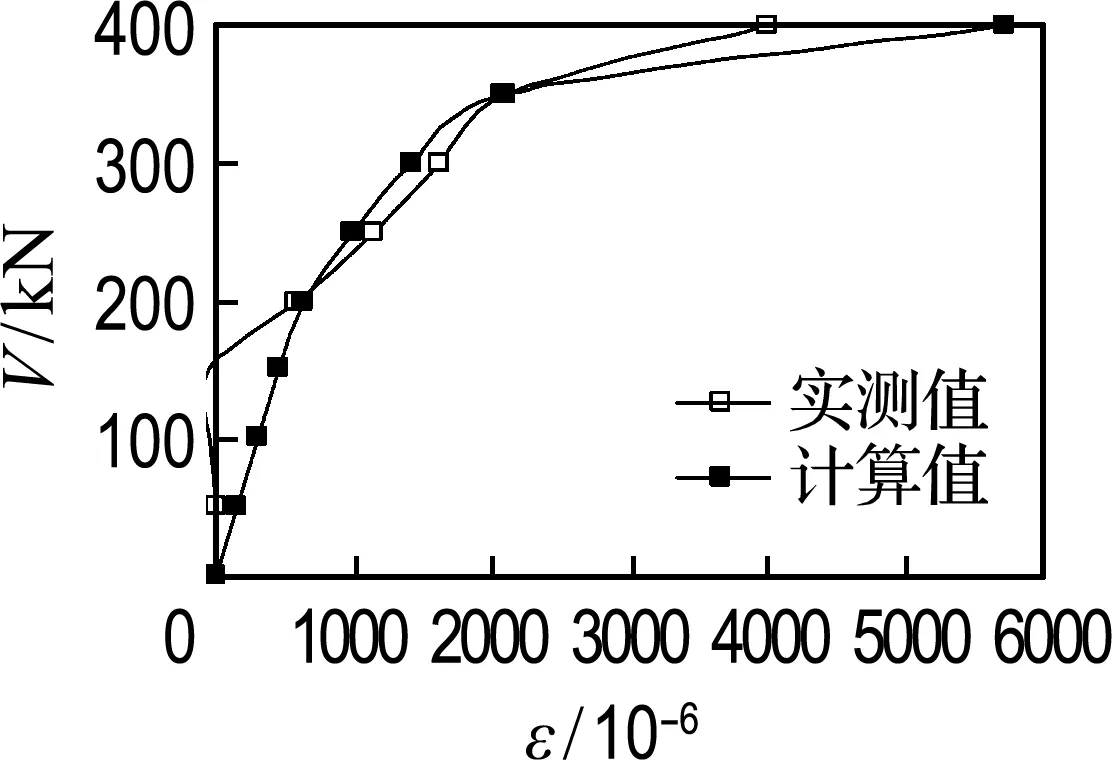
(a) LB-1

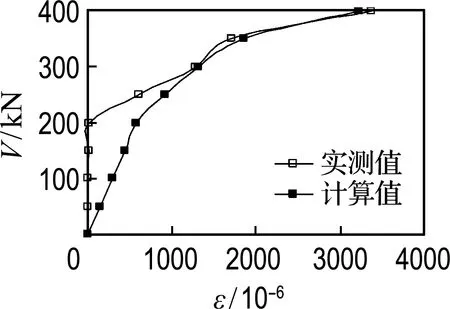
(b) LB-2

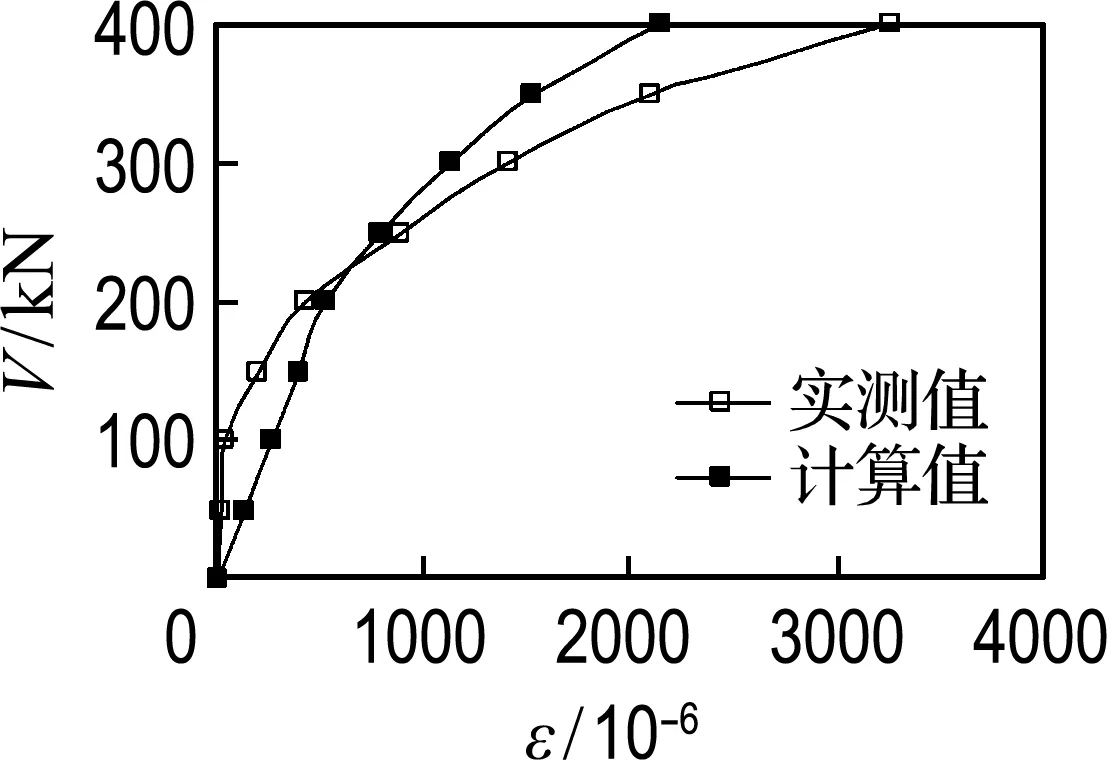
(c) LB-3

(d) LB-4

圖9 箍筋應變隨剪力的變化

Fig.9Variation of stirrup strain with shear force

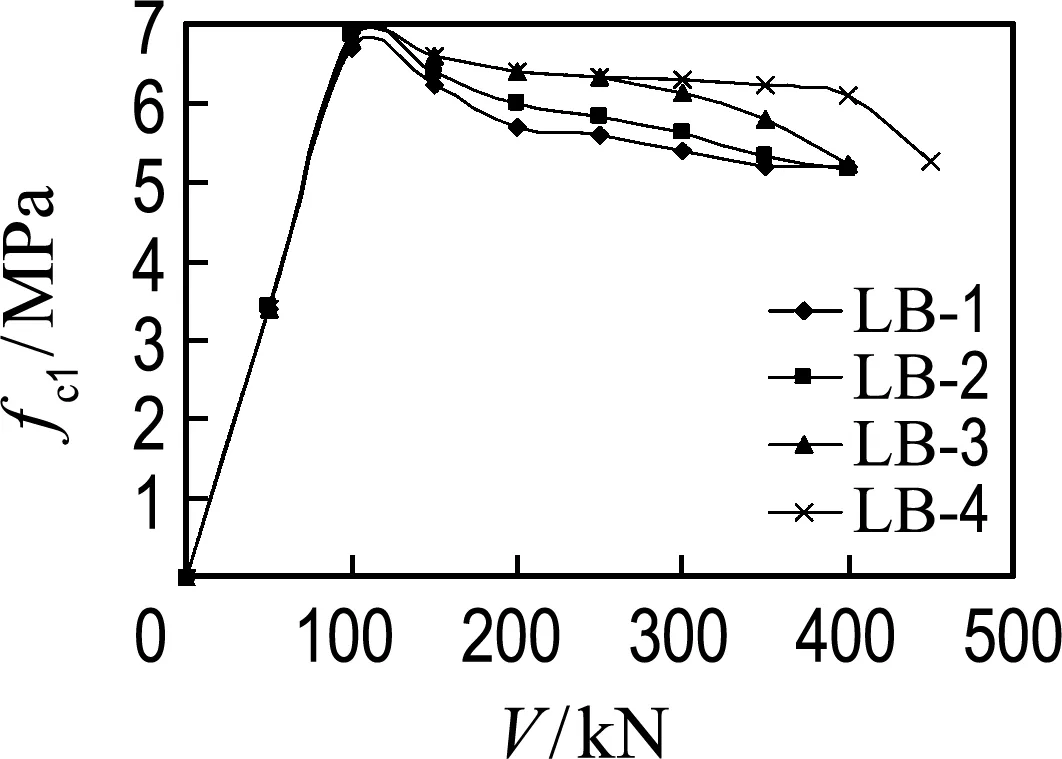
圖10 剪力-RPC主拉應力(B組)

(1)該模型更適用于以剪壓破壞形態為主的試驗梁，對于剪跨比較小、破壞形態接近于斜壓破壞的試驗梁，沒有充分考慮到加載點與支座之間RPC斜壓柱的有利影響，造成極限承載力的低估．

表5 基于MCFT的計算值與實測值比較

(2)模型沒有考慮縱筋消栓作用的影響．表中抗剪承載力隨配筋率的增加而微弱增加的原因是因為縱筋參與了彎剪承載力中的抗彎，且由文獻[19]可知，彎矩對剪力的影響十分有限，故在本模型中，配筋率與縱筋強度對極限承載力的影響也十分有限．

對比文獻[21]中的塑性理論、《混凝土結構設計規范》(GB 50010—2010)[22]以及《美國ACI規范》[23]的計算結果，并結合剪跨比、配箍率、配筋率以及縱筋強度(A、B、D、E組試驗梁)的影響，分析各方法對抗剪承載力計算結果以及對結果趨勢預估的情況，見圖11．

對比各影響因素下不同計算方法的結果，文獻[22]和[23]的計算結果偏保守，但能較好地估算出箍筋增強抗剪承載力的趨勢．塑性理論與MCFT的計算方法對抗剪承載力的預估較精準，但在計算結果的趨勢上，MCFT與試驗結果更加吻合．

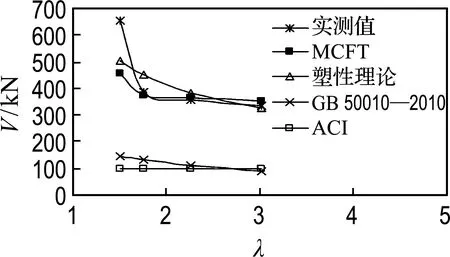
(a) 剪跨比

(c) 配筋率

(d) 縱筋強度

圖11 各影響因素下不同模型預測的抗剪承載力

Fig.11 Prediction of shear capacity under different influencing factors by different models

4 結 論

(1)基于MCFT的彎剪復合作用下截面分析模型能很好地模擬計算配筋RPC梁彎剪段的整個受荷過程，模型預估的箍筋平均應變隨荷載的變化規律與實測情況較為符合，能表現出受荷后期彈塑性變化的趨勢．

(2)在計算跨越裂縫的力的平衡時，由于RPC去粗骨料而含有鋼纖維的材料特性，原本普通混凝土粗骨料的咬合力則被RPC中鋼纖維的抗拔阻力所代替．模型預測的精準性受RPC的受拉本構關系的影響較大，不僅直接影響計算構件的開裂荷載，還可根據該關系估算出破壞時截面上殘留的平均拉應力，從而為評估構件延性性能創造條件．

(3)基于MCFT預測的配筋RPC梁抗剪極限承載力與實測值的誤差較小，優于現行規范，且從對4種影響因素(剪跨比、配箍率、配筋率和縱筋強度)所得結果的走勢上看，還略優于塑性理論的計算結果．

(4)該模型更適用于以剪壓破壞形態為主的構件，由于未充分考慮到加載點與支座之間RPC斜壓柱的有利影響以及縱筋消栓作用的影響，會低估剪跨比較小、破壞形態接近于斜壓破壞構件的極限承載力，同時也未體現縱筋對極限承載力的影響．