聚類系數和度相關性均可調的HK擴展模型

周玉江,王 娟

(深圳大學 信息工程學院,廣東 深圳 518060)(*通信作者電子郵箱juanwang@szu.edu.cn)

0 引言

通過研究網絡的生長演化模型,可以更好地了解網絡的演化規律和形成過程，并且針對社交網絡拓撲特性的研究有助于深入認識社交網絡的形成過程。

現實生活中,很多復雜網絡都具備一些共同的特征,如:高聚類系數、小世界、冪律型度分布等。為了解釋冪律分布,學者Barabási和Albert提出BA模型[1],解釋了冪律分布產生機理;但BA模型產生的網絡,聚類系數幾乎為0,為提高BA模型的聚類系數,Holme和Kim提出HK模型[2],該模型具有較高的聚類系數。受到HK模型啟發,此后眾多學者提出各種適用場合的網絡演化增長模型。

錢大千等[3]根據現實社交網絡中的熟人推薦原理,提出二步式增長模型(Two-Stage Growth Model, TSGM);王丹等[4]考慮到網絡中的舊節點也會發生連接,將 HK 模型中的三角結構擴展到了舊節點之間, 并且考慮到每個時間步新增邊的數量不是固定值,提出了度分布和聚類系數可調的擴展HK(Extended HK, EHK)模型;Li等[5]同樣考慮到舊節點之間也會發生連接,提出一個聚類系數可調的擴展HK模型;徐玉珠等[6]考慮到在新節點加入時, 可能是單個節點也可能是一個社團, 并且將熟人推薦連接機理應用到舊節點之間進行網絡演化，提出了兩個度分布與聚類系數均可調的改進HK網絡模型;崔愛香等[7]考慮網絡演化時會出現加速增長這種情況,提出一種改進的加速增長HK演化模型;李穩國等[8]考慮到每個節點在加入網絡時,添加的邊數可能不同,提出改進的HK模型。

盡管以上復雜網絡增長演化模型抓住了復雜網絡演化的基本特征:增長和擇優,構造的網絡能符合冪律型度分布的特征,但忽略了網絡的度相關性。現實生活中,所有的生物網絡和技術網絡都是負相關的,但是大多社交網絡卻是正相關,即度值較大的節點更傾向于連接度值較大的節點。高聚類特性和度正相關特性是社交網絡的顯著特征[9-10]。

最近,一些研究正負相關性可調的網絡增長演化模型被提出來。Wang等[11]在權重網絡中,將初始吸引度加入到雙向選擇機制中[12],從而成為了新的雙向吸引機制,該模型生成的網絡具有正負相關性可調的特性;劉建國[13]先提出一個兩步增長模型，隨后在兩步增長模型的基礎上又提出一個度相關性正負可調的復雜網絡增長演化模型,通過調節擇優參數達到調整網絡正負相關性的目的;Catanzaro等[14]在BA模型的基礎上,以概率p增加舊節點之間的連接,且舊節點之間的連接以條件概率p(k2|k1)進行,通過調節p可以實現網絡正負相關性可調的特性。以上網絡增長演化模型未能采用HK模型中的聚類系數可調的優點。

本文在HK增長模型的基礎上作出改善,提出聚類系數和度相關性均可調的HK擴展模型(HK extended model with Turnable Degree Correlation and Clustering coefficient, HK-TDC&C)。用該模型能生成各種拓撲的網絡,包括高聚類、度相關為正的社交網絡。

1 社交網絡的統計參量

常用以下統計參量來刻畫社交網絡拓撲結構:

1)度分布p(k)。

在網絡中隨機抽取一個節點i,它的度為k的概率可表示為p(k),p(k)通常稱為度的分布函數,簡稱度分布。

2)平均聚類系數C。

社交網絡是社會關系的一個反映,在許多真實的社交網絡中,一個用戶的朋友圈的成員之間的聯系通常比較緊密,可用聚類系數刻畫這種關系。聚類系數就是一個用戶連接中實際存在的三角形數量與所有可能存在的三角形數量之比。平均聚類系數是網絡中所有節點聚類系數之和與網絡節點總數的商。

3)平均最短路徑L及網絡直徑D。

網絡的平均最小路徑定義為網絡中所有兩兩節點之間最短距離的算術平均值;而網絡直徑定義為所有兩兩節點之間最短距離的最大值。

4)度相關性r。

Newman利用Pearson相關系數r來描述度的相關性:通過任意一條邊都可以找到兩個節點,進而得到兩個節點的度值,這樣遍歷所有的邊得到了兩個序列,分析這兩個序列的相關性,即為網絡的度相關性,用公式[15]可以表示為:

(1)

其中:ki、ji分別為第i(i=1,2,…,M,M為網絡的總邊數)條邊的兩個端點的度值。

相關系數r∈[-1,1]。當r<0時,表示網絡是負相關的,即異配網絡;當r>0時,網絡正相關的,即同配網絡;當r=0時,網絡是不相關的。

近期研究發現,大部分社交網絡是正相關的,而技術網絡、生物網絡是負相關的。

2 現實中的社交網絡拓撲結構

本文所用數據集為斯坦福大學收集的Facebook的社交數據[16],該數據集抓取節點4 039個,邊88 234條,平均聚類系數C=0.605 5。

計算該網絡的以下拓撲參數:平均最短路徑、平均聚類系數、相關系數和度分布函數。相關數據如表1所示。

表1 Facebook網絡拓撲參數Tab.1 Facebook network topological parameters

通過分析表1,可以發現該網絡具有典型的社交網絡特征:小世界特性(L=3.690 7)、較高的聚類系數(C=0.605 4)和正相關性(r=0.206 3)。

此外,節點的度分布也是描述一個網絡的重要特征, Facebook網絡的度分布雙對數曲線如圖1所示。

圖1 Facebook社交網絡度分布曲線Fig. 1 Social network degree distribution curve of Facebook

從圖1可以看出,Facebook網絡的度分布符合冪律分布的特征。

3 聚類系數和度相關性可調的HK擴展模型

利用建模的方式研究網絡結構的方法由來已久。早在20世紀60年代,Erds和Rényi[17]利用隨機圖理論構建了隨機網絡,稱為ER模型,開創了用隨機理論創建網絡的先例;隨后Barabási和Albert[1]對已有的網絡模型進行分析后,對網絡增長演化模型進行改進,提出實際網絡增長過程中具備的兩個重要特性:增長和擇優。基于以上兩個特性,文獻[1]于1999年提出了一個無標度網絡模型。但BA模型產生的網絡,聚類系數幾乎為0,為提高BA模型的聚類系數,Holme和Kim提出HK模型[2],該模型具有較高的聚類系數。

HK模型是高聚類系數網絡增長演化模型的代表, 在BA模型擇優連接(Preferential Attachment, PA)的基礎上,引入三角連接(Triad Formation, TF)方法。該模型算法步驟為:首先按照PA步驟連接網絡中的一個節點;然后以概率p進行TF方式連接或者以概率(1-p) 再次進行 PA 方式連接, 增加其余的(m-1) 條邊,使得網絡聚類系數隨參數p變化。

3.1 本文提出的演化增長模型HK-TDC&C

HK模型可以同時實現網絡的高聚類系數和無標度特征, 成功地實現了復雜網絡中小世界特征與無標度特征的統一。但該模型在連接時,過分強調度基于度值的優先連接,所以新加入的節點更傾向于連接度值最大的節點,造成網絡度值出現負相關的情況。

本文在HK模型的基礎上進行改進,提出HK-TDC&C模型。該模型在上述TF連接步驟中,通過調節參數,分別實現擇優與擇弱的連接,解決HK模型中度相關性為負數的狀況,可以實現網絡的聚類系數和相關性均可調的目的。HK-TDC&C模型演化步驟如下:

1)初始狀態。網絡初始狀態含有m0個完全連接的節點。

2)每一個時間步內,一個新的節點v連同m條邊加入網絡。

3)在生成的網絡中,按照式(2)的概率,隨機選取網絡中的一個任意節點(包含初始狀態的m0個節點)i,添加一條邊。這種連接方式通常稱為PA擇優連接;

(2)

4)以概率p按照改進的三角連接(Improved Triad Formation, ITF)方式進行連接,或者以概率1-p再次進行PA方式連接, 增加其余的m-1條邊。其中p為三角連接概率。

ITF規則是指對于已經選定的一個節點i, 按照式(3)的概率隨機選取它的一個鄰居節點a進行連接。

(3)

其中:Γ(i)表示節點i的鄰居節點集合。β稱為擇優參數,用于調整網絡的度相關性。當β>0時,度值高的節點有較高的連接概率,屬于擇強連接;當β<0時,度值低的節點有較高的連接概率,屬于擇弱連接;當β=0時,節點i的所有鄰居節點被選中的概率相同,此時改進模型與HK模型等同。

在HK-TDC&C網絡演化模型中,步驟3)的PA連接和步驟4)的ITF連接,這兩種連接方式可用圖2作進一步說明。

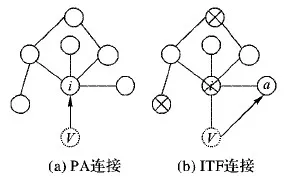
圖2 PA連接方式和ITF連接方式Fig. 2 PA connection method and ITF connection method

圖2(a)表示PA連接方式:新節點加入網絡時更傾向于連接度值較大的節點;圖2(b)表示ITF連接方式,選定節點i的非鄰居節點(圖中以畫叉節點表示)不能選,只能按照式(3)的概率,隨機選取節點i的鄰居節點進行連接,如連接節點a。

5)返回步驟2),直到滿足終止條件:網絡的規模N達到所希望的值,生成了一個節點數為N的網絡。

3.2 度分布的分析

根據3.1節對HK_TDC&C模型的描述,采用連續場理論[1]。在該模型中,研究網絡中某一節點i的度值ki隨時間的變化,假設其度值是連續變化的,則如下表達式成立:

(4)

其中:m是每個時間步時加入的邊數量；G為網絡中所有節點的集合。

以下分別詳細討論擇優參數β取值為0和非0的情況,對度分布產生的影響。

1)β=0的情況。

由式(4)可以得到如下等式成立:

(5)

由于網絡中節點數量之和等于邊的數量之和的兩倍,每一時間步t有下式[1]成立:

(6)

將式(6)代入式(5),并解微分方程可以得到:

(7)

該微分方程的初始條件為:

ki(ti)=m

(8)

式(8)表示在ti時刻節點i的度值為m。其中，ti為節點i加入網絡的時間。

例(5)：If he buys two cents worth of peanuts, his father says, “ Remember what Franklin has said, my son- ’ A groat a day’s a penny a year ”

由初始條件,可以得到方程式(7)的解為:

ki(t)=m(t/ti)1/2

(9)

其中:t表示網絡建立的總時間。可以看出,ti越小(即節點加入網絡越早),度值越大,符合社交網絡“富者越富”的現象。

假定用戶節點都是等時間間隔加入到網絡系統,則ti是一個均勻分布,密度函數可寫為:

(10)

結合式(9),ki的分布函數可以表示為:

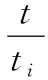
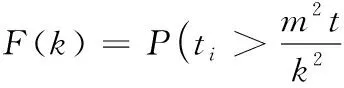
(11)

(12)

所以度的分布函數為:

(13)

系統在經歷過足夠長的時間后,當t→ ∞,式(13)可寫為:

p(k)=2m2·k-3

(14)

綜上所述,在β=0時,HK-TDC&C模型完全符合冪律分布的特征,且γ=3。

2)β≠0的情況。

(15)

由式(15)可以得出該模型的度分布并非嚴格服從冪律分布的結論。而通過分析圖1中Facebook社交網絡的雙對數曲線,可以看出:現實網絡中的度分布具有冪律分布的趨勢,而并非嚴格地服從冪律分布。因此,HK-TDC&C模型可以理解為在嚴格的冪律分布的基礎上疊加了一些噪聲。

可以通過調節模型中的參數:連接概率p及擇優參數β,對網絡的聚類系數、度相關性進行修正,使之能更好地接近現實中的社交網絡。

4 實驗與評估

下面通過仿真的方法,按照HK-TDC&C模型算法生成一個網絡,并分析該網絡的各拓撲參數:度分布特征P(k)、平均最小路徑L、聚類系數C、度相關性r。

實驗參數設定如下:初始網絡節點數m0=20,每步添加的邊數m=18,網絡節點數量N=2 000,p和β作為網絡的調節參數。

1)擇優參數β對網絡結構的影響。

取p=0.8,當擇優參數β=-0.8,0,0.8時,生成網絡的各參數如表2所示。

表2 擇優參數β對網絡的影響Tab.2 Influence of preferred parameters β on the network

通過分析表2,可以得出:

①當β取值為負值時(β=-0.8),可以生成正相關網絡。對比表1中的Facebook網絡數據,可以看到,網絡的各項參數,如網絡直徑D、平均最小距離L、度相關系數r,都能較好地符合真實社交網絡特征。平均聚類系數C有待進一步提高,但在大多數社交數據集中,平均聚類系數C通常為0.2左右[9]。

②當β取值為0時,HK-TDC&C模型與HK模型等同。可以發現,HK模型及其后的擴展模型[3-8],由于未采用擇優參數進行調節,生成的是不相關網絡(或稱為較弱的負相關網絡),這是該類模型的共同特征。

③當β取值為正時,可以生成負相關性的網絡。

2)連接概率p對網絡結構的影響。

取β=-0.8,當p=0.2、0.5、0.9時,生成網絡的各參數如表3所示。

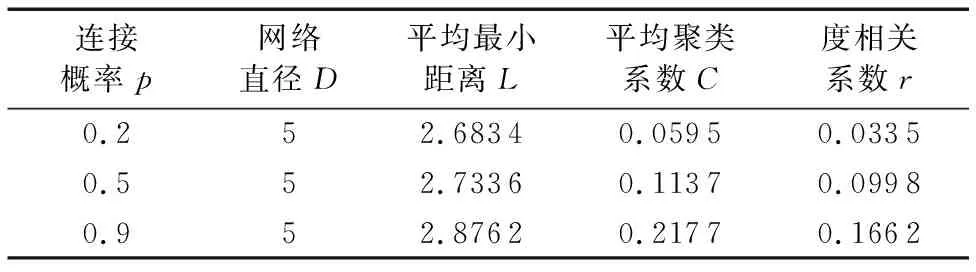
表3 連接概率p對網絡的影響Tab.3 Influence of connection probability p on the network

通過表3,可以看出:聚類系數和度相關系數都與擇優參數p正相關,即p取值越大,聚類系數和度相關系數也越大。

3)網絡的度分布情況。

取p=0.8,β=-0.8,0,0.8的情況下,度分布雙對數曲線如圖3所示。

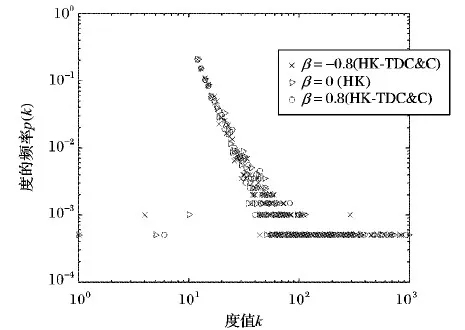
圖3 HK-TDC&C網絡度分布曲線(p=0.8)Fig. 3 HK-TDC&C network degree distribution curve (p=0.8)

通過圖3可以看到:HK-TDC&C模型構建的網絡,它的度分布符合冪律分布的特征。

4)基于上述1)、2)、3)項對HK-TDC&C模型的數據分析,可以看到,在β取負值(如-0.8),p取值較高(如 0.8)的情況下,該模型生成的網絡能較好地符合社交網絡的基本特征:度值服從冪律分布、度的正相關性、較高的聚類系數、較短的平均距離。因此該模型可用來生成各種拓撲結構的社交網絡。

5 結語

本文以HK模型為基礎,提出了一種新型的社交網絡建模方法:通過調節擇優參數β實現不同程度的擇優或擇弱連接,實現網絡正負相關性可調的目的。仿真結果表明,通過選取適當參數,該模型生成的社交網絡具有的拓撲特征與社交網絡相符,包括:高聚類系數、較短的平均最短路徑、度的冪律分布特性、度的正相關特性。本文算法構造的社交網路與真實社交網絡各參數相比,較為接近。