基于混沌映射的多因子認證密鑰協商協議
王松偉,陳建華
(武漢大學 數學與統計學院,武漢 430072)(*通信作者電子郵箱wangsw_ecc@163.com)
0 引言
隨著互聯網各種應用需求的快速增長,網絡廣泛應用于商業、交通、政務、娛樂、醫療等領域,如醫生通過遠程醫療信息系統可以給患者提供方便快捷的電子醫療服務,同時由于網絡的開放性,病人的醫療記錄等隱私需要保護以避免信息泄露。為了保護用戶的安全和隱私,近年來海內外學者提出了一系列協議。比如,基于口令的單因子認證協議[1],基于口令+智能卡的雙因子認證協議[2],基于口令+智能卡+生物特征的多因子認證協議[3]。
2013年Guo等[4]提出了一個基于智能卡的認證協議,隨后Hao等[5]指出其不能保護用戶匿名性,并提出了一個新的認證協議。但是Lee[6]和Jiang等[7]指出Hao等[5]不能抵抗智能卡丟失攻擊和Bergamo攻擊[8]等問題。2014年,Xu等[9]提出了一個基于橢圓曲線的遠程用戶認證方案。隨后,Mishra[10]指出Xu協議[9]在登錄和認證階段存在設計漏洞,接著2015年Amin等[11]發現Xu方案[9]口令修改效率低下,并提出一個新的協議。2016年Zhang等[3]提出了一種基于混沌映射的認證密鑰協商協議,接著王彩芬等[12]通過分析Zhang等[3]方案,發現并不能抵抗內部攻擊。Park等[13]提出的基于橢圓曲線的三因子認證協議,也被發現無法提供用戶匿名性且存在字典攻擊;Jung等[14]提出的匿名認證協議則無法保護用戶匿名性,存在字典攻擊、內部攻擊且不具備前向安全性;Jiang等[15]提出的三因子認證協議也無法保護用戶匿名性,不能提供前向安全性且存在字典攻擊。針對以上問題,Wang等[16-18]指出設計實現用戶匿名性或多因子安全性的身份認證協議,必須采用公鑰密碼技術。傳統的公鑰密碼技術主要基于以下數學難題:大整數因子分解難題、離散對數難題、橢圓曲線離散對數難題。由于切比雪夫多項式混沌映射相比傳統公鑰算法具有較高的計算效率,2017年Li等[19]提出了一個更安全的基于混沌映射的醫療信息系統遠程用戶認證方案。
本文簡單回顧文獻[19]的方案并指出其不能抵抗用戶冒充攻擊,容易遭受拒絕服務攻擊,且無法確保用戶身份唯一性。本文提出了一個基于混沌映射的三因子認證密鑰協商協議方案,最后對協議進行安全性分析和性能分析,并與已有協議進行比較,表明本文協議更加安全高效和實用。
1 預備知識
1.1 切比雪夫多項式
定義1 切比雪夫多項式[20]。設n為正整數,x∈[-1,1],n階切比雪夫多項式Tn(x)定義如下:
Tn(x)=cos(n×arccos(x))
(1)
此外,切比雪夫多項式還有一種等價的遞歸定義如下:
Tn(x)=2xTn-1(x)-Tn-2(x)
(2)
其中:n≥2,T0(x)=1,T1(x)=x。
性質1 半群性質[8]:
Tr(Ts(x))=Trs(x)=Tsr(x)=Ts(Tr(x));r,s∈N
(3)
2008年,Zhang[21]證明了切比雪夫多項式在區間(-∞,+∞)上仍然具有半群特性。
定義2 擴展切比雪夫多項式。設n為正整數,x∈(-∞,+∞),則定義在區間(-∞,+∞)上的n階擴展切比雪夫多項式Tn(x)為:
Tn(x)=cos(n×arccos(x)) modp
(4)
其等價的遞歸定義:
Tn(x)=2xTn-1(x)-Tn-2(x)(modp)
(5)
其中:n≥2且p是一個大素數。這里T0(x)=1,T1(x)=xmodp。顯然,式(5)同樣具有半群性質,即:
Tr(Ts(x))≡Trs(x)≡Tsr(x)≡Ts(Tr(x))(modp);
r,s∈N
(6)
1.2 切比雪夫多項式數學難題
多項式時間內求解以下問題是困難的[21]:
問題1 混沌映射離散對數問題。給定x,p,以及y=Tr(x)(modp),找到一個正整數r,使得Tr(x)(modp)≡y。
問題2 混沌映射計算Diffie-Hellman問題:給定p,x,以及Tr(x)(modp)和Ts(x)(modp),找到一個正整數y,使得Trs(x)(modp)≡y。
1.3 模糊提取器
生物特征如指紋、臉、虹膜、掌紋等,具有普遍性、唯一性、穩定性、識別率高和不可復制等特性,因而成為個人身份鑒別與識別的重要依據,在密碼協議中得到廣泛應用[13-15,22]。 Dodis等[23]提出的模糊提取器很好地解決了生物特征應用中的難題;當兩次輸入的BIO′和BIO相差不大時,模糊提取器可以輸出一個一致的隨機字符串σ。服務器等設備只需存儲隨機字符串σ,而無需存儲用戶生物特征。
模糊提取器可用算法函數〈Gen,Rep〉表示:Gen是一個隨機數生成算法函數Gen(BIO)=(σ,θ),當輸入生物特征BIO時,Gen將輸出一個隨機字符串σ和一個輔助隨機字符串θ,其中:σ為安全參數;Rep是一個隨機恢復算法函數σ=Rep(BIO′,θ)。模糊提取器在接收到一個誤差允許范圍內的生物特征BIO′以及相應的隨機輔助字符串θ時,若dis(BIO′,BIO)≤ε,則恢復出對應的字符串σ,其中:dis(BIO′,BIO)≤ε表示BIO′和BIO的距離不超過一個給定的區間ε。
2 Li協議方案
本章對Li協議[19]作一個簡單的回顧。
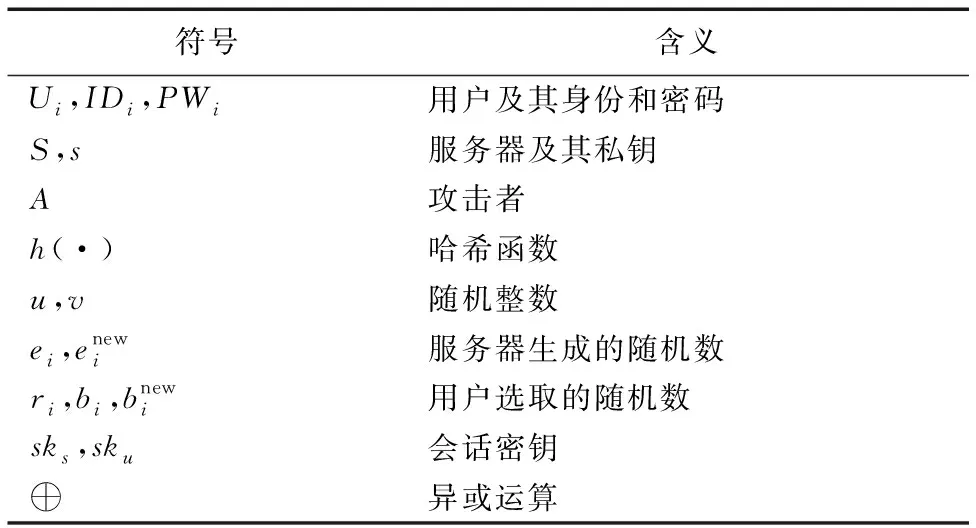
表1 Li協議[19]中到的符號說明Tab. 1 Symbol description of Li protocol[19]
2.1 注冊階段
1)用戶Ui選取身份IDi和口令PWi,通過安全信道發送IDi給服務器S。
2)服務器生成隨機數ei并計算CIDi=h(IDi,ei),B0=h(CIDi,s),通過安全通道發送B0,CIDi給Ui。
3)用戶選取隨機數bi,計算HPWi=h(PWi,bi),B1=B0?h(IDi,HPWi),B2=h(IDi,PWi)?bi,并將數據(B1,B2,CIDi)存儲到移動設備中。
2.2 登錄階段
1)用戶Ui輸入用戶名IDi和密碼PWi,計算bi=B2?h(IDi,PWi),HPWi=h(PWi,bi)。
2)用戶選取隨機數u、ri,計算C1=B1?h(IDi,HPWi)?ri,C2=Tu(x),C3=h(ri)?IDi,C4=h(IDi,CIDi,ri,C2,C3),通過公共信道發送M1={CIDi,C1,C2,C3,C4}給S。
2.3 認證階段
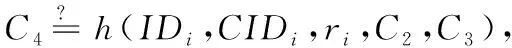

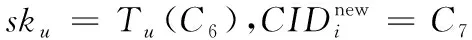
3 Li協議的安全性分析
3.1 用戶冒充攻擊
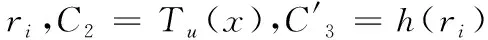
3.2 拒絕服務攻擊
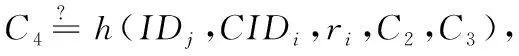
3.3 無法確保用戶身份唯一性
在實際中,很有可能兩個不同用戶選擇了相同的身份,按照Li方案[19],這兩個用戶都可以注冊成功,而且也都是合法用戶,也可以登錄同一個服務器,然而服務器卻無法區分他們,這可能會產生嚴重問題。
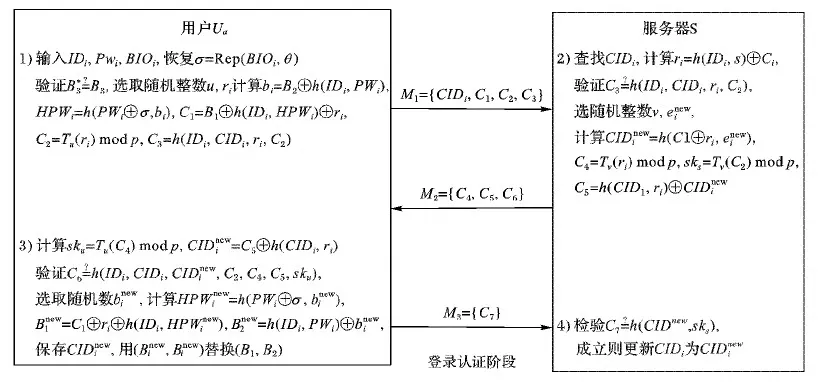
圖1 新協議的認證過程Fig.1 Certification process of new protocol
4 本文協議
本文提出了一個新的基于擴展混沌映射的三因子認證協議。新協議包括:注冊、登錄認證、口令修改以及注銷等四個階段。相關符號的含義如表2所示。
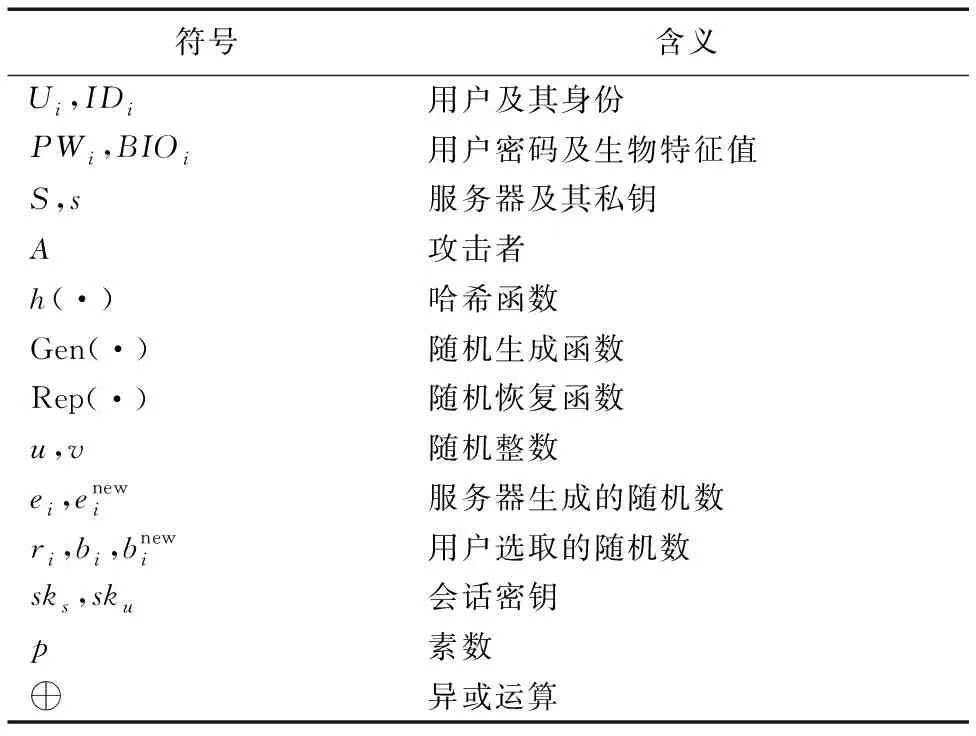
表2 本文協議中的符號說明Tab. 2 Symbol description of the proposed protocol
4.1 注冊階段
1)用戶Ui選取身份IDi和口令PWi,通過安全信道傳送IDi、生物信息BIOi給服務器S。
2)服務器收到用戶注冊請求之后,首先查找IDi是否已存在,若存在,表明該ID已經被注冊,拒絕用戶注冊請求;若不存在,將生物信息輸入到模糊提取器得到一個隨機字符串σ和一個輔助隨機字符串θ,即Gen(BIOi)=(σ,θ)。S選取隨機數ei,并計算B0=h(IDi,s),CIDi=h(B0,ei),通過安全信道發送消息B0,CIDi,θ,Rep(·),p給Ui,其中p為素數,同時在后臺數據庫添加(IDi,CIDi),將BIOi刪除。
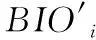
4.2 登錄認證階段
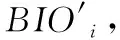
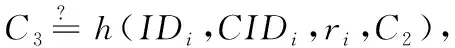
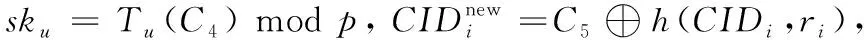

由于C2=Tu(ri) modp和C4=Tv(ri) modp,則有
sks≡Tv(C2)≡Tv(Tu(ri))≡Tvu(ri)≡
Tuv(ri)≡Tu(Tv(ri))≡Tu(C4)≡skumodp
所以本文方案是正確的。
4.3 口令修改階段
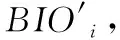
4.4 注銷階段
當用戶不再使用該服務時,Ui可以向服務器申請注銷其賬號,服務器在驗證了用戶Ui的身份之后,在用戶數據庫中找到其IDi,然后將(IDi,CIDi)從數據庫中刪除即可。
5 新協議方案分析
5.1 安全性分析假設
定義方案安全性分析的安全假設如下:
假設1 攻擊者可以截獲公開信道上的信息,且能夠對信息進行修改和重放,攻擊者獲得用戶的設備后可以利用能量分析等方法(Kocher等[24]、Messerges等[25]、Brier等[26])獲取設備中存儲的數據。
假設2 服務器的主密鑰s、哈希函數是安全的,即攻擊者在多項式時間內無法解決這些問題。
5.2 新協議安全性
在以上安全假設下,下面分析本文方案的安全性:新協議給每個用戶分配動態身份保護用戶匿名性,所以這里假設攻擊者已經鎖定了目標用戶。
1)抵抗Bergamo攻擊:Bergamo攻擊[8]中,攻擊者必須得到x,Tr(x)和Tk(x)三個元素,才能發動有效攻擊。本文協議采用擴展的切比雪夫多項式,采用了模運算,而且x∈(-∞,+∞)能夠效避免三角函數的周期性。

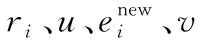
4)抗口令猜測攻擊:本文協議沒有在線對用戶口令驗證,而是驗證用戶與服務器共享的秘密值攻擊者選擇在線攻擊時,當停止會話次數達到預先定義的閾值,賬號會被鎖定,所以,本文協議可以抵抗在線猜測攻擊。對于離線猜測攻擊,假設攻擊者獲得了用戶的設備,即使攻擊者可以同時猜測用戶的身份和口令,由于B3=h(σ,IDi?PWi)modn,攻擊者卻無法驗證猜測口令的正確性。
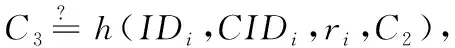
6)抗設備丟失攻擊:假設攻擊者獲得Ui的設備,并通過能量分析獲得設備中的信息(B1,B2,B3,CIDi,θ,Rep(·),p),由以上分析可知,攻擊者并不能得到用戶的口令,也無法偽造用戶的生物信息。
7)抗重放攻擊和冒充攻擊:本文協議中用戶每次均采用動態身份登錄,攻擊者直接重放以前經過雙方認證的消息很容易被識破,攻擊者只能冒充合法用戶或者服務器嘗試構造正確的消息進行攻擊。
(a)攻擊者M冒充用戶:假設攻擊者獲得了用戶的移動設備并獲得用戶的CIDi,然后冒充用戶。因為C1、C2、C3都與隨機數ri有關,因此攻擊者若要冒充用戶,必須構造C1、C2、C3,攻擊者無法獲得用戶的口令,更不可能獲得服務器密鑰s,所以很難偽造出C1。
(b)攻擊者M冒充服務器:因為用戶每次登錄選擇不同的隨機數ri,顯然直接重放消息M2={C4,C5,C6}無效,攻擊者只能嘗試構造C4、C5、C6,攻擊者必須先計算出ri,而ri=h(IDi,s)?C1,攻擊者不可能獲得服務器密鑰s,所以很難偽造出正確的ri。
8)中間人攻擊:由以上分析可知,攻擊者無法計算相關消息,簡單的消息重放很容易被識破,更不可能計算出共享會話密鑰。
9)完美前向安全性:本文協議雙方協商的會話密鑰為sks≡Tuv(ri)≡Tv(Tu(ri))≡Tu(Tv(ri)) modp,假設攻擊者獲得系統密鑰和用戶的口令,通過公開信道截獲到會話密鑰的兩個元素Tu(ri) modp和Tv(ri) modp然而攻擊者在不知道隨機數u或v的情況下,計算Tuv(ri)面臨擴展切比雪夫多項式的數學難題,若攻擊者先由Tu(ri) modp和Tv(ri) modp計算出u或v也面臨擴展切比雪夫多項式的數學難題。
10)已知會話密鑰安全性:已知會話密鑰安全性是指通信雙方產生的會話密鑰之間應該相互獨立。本文協議會話密鑰sks≡Tuv(ri)≡Tv(Tu(ri))≡Tu(Tv(ri)) modp,其中u和v是用戶和服務器選取的一次性隨機數,所以即使攻擊者獲得了某一次的會話密鑰sk,他也不可能計算出下一次的會話密鑰sk′。
5.3 性能分析
本節將新協議同Xu協議[9]、Mishra協議[10]、Amin協議[11]、Zhang協議[3]、Li協議[19]進行比較。
從表3的分析結果來看,本文協議方案在功能上明顯優于其他的認證協議方案。
5.4 計算效率分析
表4對比了計算效率,符號含義如下:Th表示計算一次哈希函數值所需時間;Tc表示計算一次切比雪夫多項式所需時間;Ta表示計算一次橢圓曲線點加所需時間;Te表示計算一次橢圓曲線點乘所需時間;Ts表示進行一次對稱加密(或解密)所需時間。
依據文獻[27]可知:Te>Ta?Th,Tc≈70Ts≈175Th,Ts≈2.5Th。由于協議的主要運算在登錄和認證階段,所以表中僅使用這兩個階段進行性能比較。從表4的結果來看,本文方案僅需4Tc+15Th,雖然文獻[10]方案比本文方案要快,但文獻[10]不能抵抗重放攻擊、設備丟失攻擊及中間人攻擊,很顯然本文方案計算性能明顯優于其他方案。
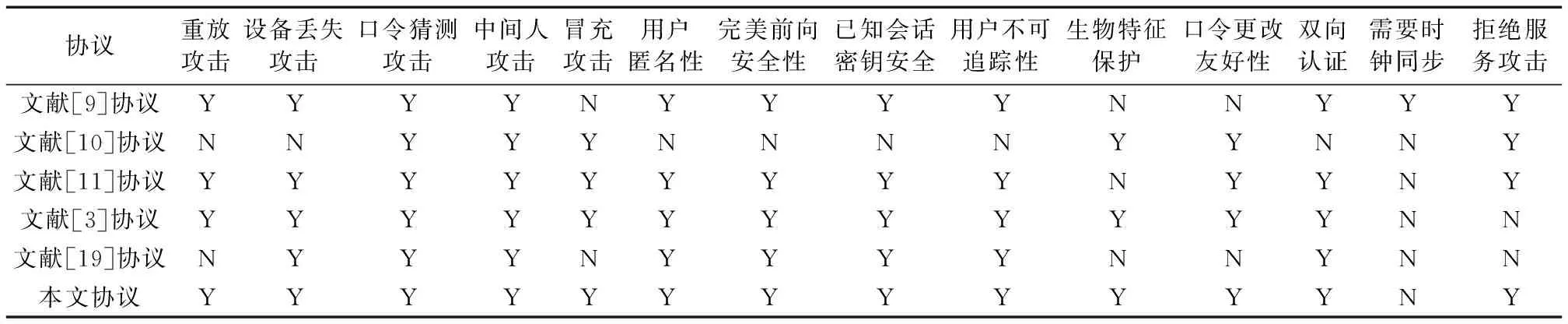
表3 不同協議的功能對比Tab. 3 Functional comparison of different protocols

表4 不同協議的計算效率對比Tab. 4 Computational efficiency comparison of different protocols
6 結語
通過分析Li方案,指出其不能抵抗用戶冒充攻擊,容易遭受拒絕服務攻擊等缺陷。本文提出了一個三因子認證密鑰協商協議,通過使用擴展混沌映射,采用三次握手技術實現異步認證,保護用戶匿名性和身份唯一性,安全性分析和性能分析結果表明,新協議不僅可以抵抗常見攻擊,滿足必要的安全需求,還具有較高的計算效率,因此,新協議具有更高的實用性。

