題根（計數原理）

倪偉

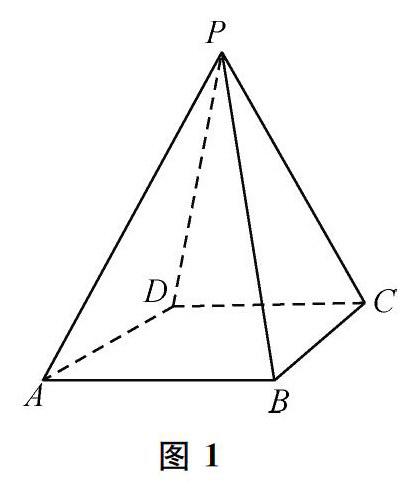
題 （1）如圖1，將一個四棱錐P-ABCD的每個頂點染上一種顏色，并使同一條棱的兩端異色，若只有5種顏色可供使用，求不同的染色方法總數.

（2）甲、乙、丙3人互相傳1只籃球，開始球在甲手中，經過5次傳球后，球還在甲手中，求不同的傳球方法總數.

一、尋根

這兩道題目的共同點在于都是計數問題，計數問題最根本的解決方法是一一數之（枚舉法）和綜合利用計數原理（分類與分步計數原理）.對于題（2），方法種數不多，可以使用枚舉法，但是為了更好地解決一類問題，我們常常需要建立一些數學模型.

如若題（1）中去掉“四棱錐”的這一包裝，題即變為：用5種顏色給P，A，B，C，D5個點染色，每個點染一種顏色，相鄰兩點不同色.五點中，除A與C、B與D不相鄰，其余都相鄰，求不同的染法種數.在解決該問題時，我們可以聯想計數問題中的一道經典染色問題（見題根）.

題（2）是一個傳球問題，和題（1）能否聯系起來呢？亦即是要找到題中的“點”和“顏色”，若我們將甲、乙、丙看作“點”，傳球方式看成在染色，發現難以轉化，因為無法理解相鄰異色.而本題中隱藏條件“自己不能傳給自己”疑似和“相鄰兩點不同色”相關，因此我們可以試著將傳給誰看成染什么色，把5次傳球看作5個“點”，問題即轉化為：用紅、黃、藍三種顏色給P，A，B，C，D5個點染色，每個點染一種顏色，相鄰兩點不同色，其中點D只能染紅色，P，A，B，C，D圍成一圈，依次相鄰，如圖2所示，因此我們可以發現這兩道題都可以看成同一類問題——染色問題.

二、題根

題根：如圖3，用5種不同的顏色給圖中4個區域染色，每個區域染一種顏色，要使相鄰區域不同色，求不同的染色方法種數.

分析一：首先我們要搞清本題需要完成的一件事——將4塊區域染好顏色.

這件事我們分四步完成：

第一步：我們染1號區域，共有5種方法；

第二步：染2號區域，只能從余下的顏色中選一種，共有4種方法；

第三步：染3號區域，由于其和2號相鄰，因此也有4種方法；

第四步：染4號區域，4號和1號與3號均相鄰，而3號與1號可能同色，也可能異色，因此我們需要重新對3號區域的染色分析.完成這件事我們將其分為兩類：第一類是當3號與1號同色，則染3號區域只有1種方法，此時染4號區域，共有4種方法；第二類是當3號與1號異色，則染3號有3種方法，此時染4號區域，共有3種方法.

因此共計有5×4×（1×4+3×3）=260種方法.

分析二：上述方法，是按區域進行分步染色，我們也可以理解為這樣完成一件事——先選好顏色，再染色.通過觀察，1號區域和3號區域、2號區域和4號區域不相鄰，這兩組區域可以同色，也可以異色，因此4塊區域用到2、3或4種不同的顏色.

完成這件事我們可以分三類：

于是我們可以將該問題一般化：

用m種不同的顏色給圖4中n個區域染色，每個區域染一種顏色，要使相鄰區域不同色，求不同的染色方法種數.

我們試著按區域進行分步染色，1號區域有m種方法，2號區域有（m-1）種方法，3號區域有（m-1）種方法……（n-1）號區域有（m-1）種方法，最后染n號區域時，需要考慮1號和（n-1）號是否同色，而它們是否同色，還需思考1號和（n-2）號是否同色……如果直接去分類，就很困難了.但我們換個角度，暫不考慮n號區域受1號區域影響，直接染n號區域時，出現兩類：一類是1號區域和n號區域異色，這是我們需要的情況；另一類是1號區域和n號區域同色，這是我們不需要的，而這種情況中，我們將1號區域和n號區域看成整體，就相當于用m種不同的顏色給（n-1）個區域染色，即用遞推關系去解決問題.

通過將問題一般化，我們就得到了一個涂色問題的模型，亦即該類問題的“題根”.三、解答（1）第一步，先將P點染色，共有5種方法；第二步，再染其他4個點，相當于題根故本題共有5×84=420種方法.

（2）方法一：枚舉法（畫出樹狀圖，如圖5所示）.其右10種.

計數問題中有很多經典的模型，可以看作“題根”，在解決一些新的問題時，我們試著將問題轉化為與題根相關的問題，會達到事半功倍的效果.