相交隧道施工盾尾注漿參數(shù)對地表沉降的影響

程 揚

（銅陵學院，安徽 銅陵 244000）

由于全國地鐵的大范圍修建，必然導致地下隧道之間的交錯，這些近接交叉隧道在施工過程中會對原有的土層產生擾動引起應力重分布，進而導致地表沉降的產生。為具體研究之一現(xiàn)象，本文以合肥高鐵南站一號線與五號線交叉隧道施工為背景，運用數(shù)值模擬方法研究在不同注漿參數(shù)情況下，近接相交隧道盾構在掘進過程中引起的地表沉降分布規(guī)律。

一、工程概況

合肥地鐵一號線與五號線相交于高鐵南站：五號線盾構隧道右線長453.17m且左線長452.234m；一號線盾構隧道右線長620.37m,左線長617.78m整個區(qū)間隧道的長度為2169.69m。

一號線繁華大道站為盾構機的始發(fā)站，在進行完繁華大道至高興區(qū)之間的盾構施工后，盾構機直接掉頭、轉向，從高鐵站南端五號線的端頭井重新開始護法，下穿合寧高速公路。重疊區(qū)域一號線與五號線的具體位置為五號線的右線和左線分別與一號線左線相交，一號線位于五號線的正上方，兩條線的夾土層最小厚度約2.965m，五號線的兩條隧道分別下穿一號線左線隧道，五號線右線與一號線左線盾構區(qū)間最小處的凈距只有2.267m，與五號線右線隧道間最小凈距僅4.26m。處于高鐵南站下的地鐵五號線隧道以及一號線左線區(qū)間隧道的位置如圖1[1]。

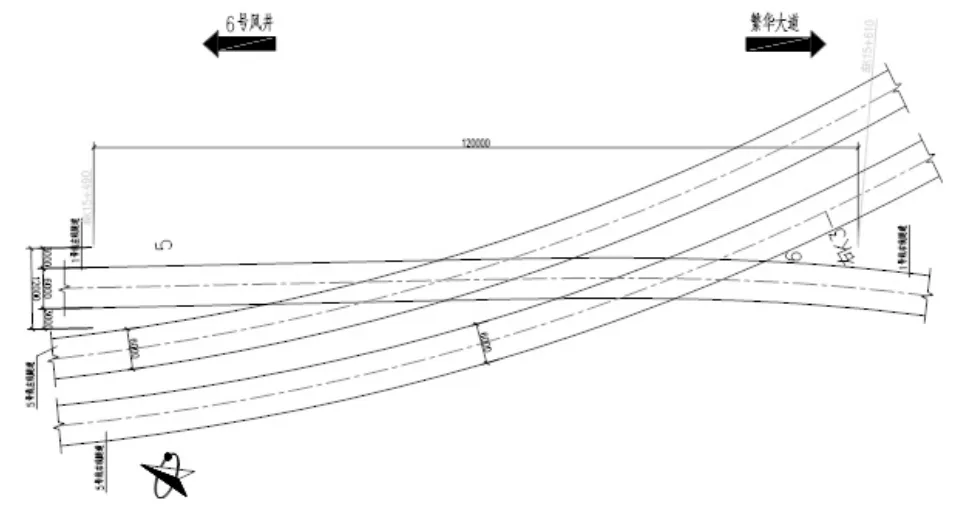
圖1 五號線隧道和一號線左線區(qū)間隧道平面關系圖

（一）場地工程地質條件

處于相交區(qū)間的土層包含下列幾層土：第一層為人工雜填土厚度約為3m，第二層為粘土約為8m，第三層土為粉質粘土約為10m。盾構隧道相交的區(qū)間位于第三層粘土，該地層主要參數(shù)見表1。

（二）管片相關參數(shù)

隧道襯砌為鋼筋混凝土管片，管片采用3+2+1模式組合，襯砌環(huán)間采用錯縫拼裝。管片寬1500mm，厚300mm，襯砌外徑6000mm，內徑5400mm，注漿層厚150 mm。襯砌采用C50的混凝土，抗?jié)B等級P12，注漿混凝土強度等級C20。具體參數(shù)見表2。

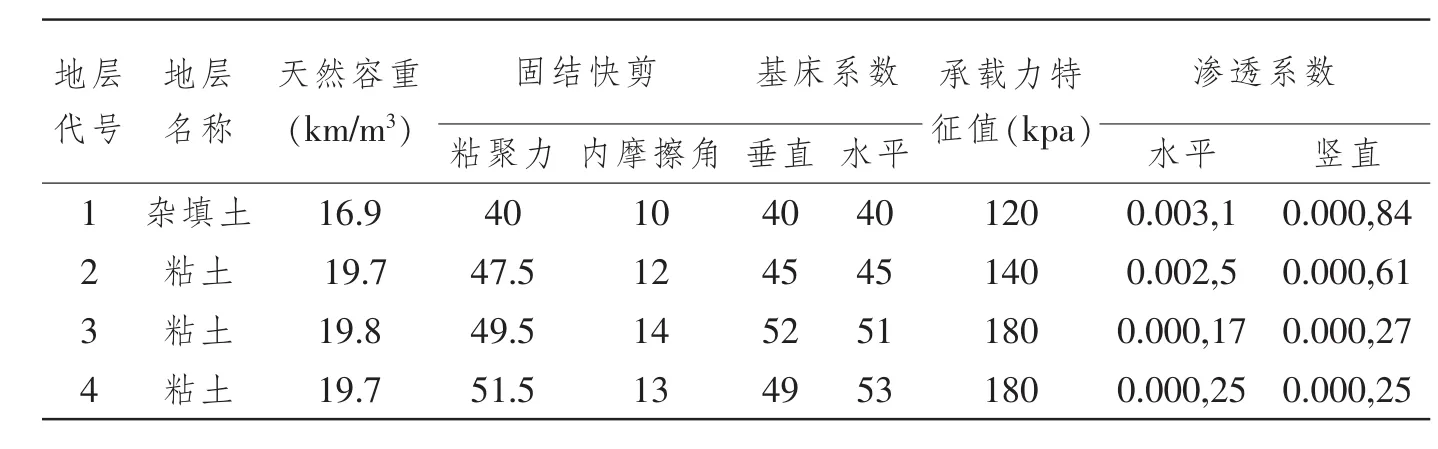
表1 各個土層詳細參數(shù)表

表2 混凝土材料計算參數(shù)

（三）盾構機主要參數(shù)

表3 盾構機主要參數(shù)

二、有限元模型建立

（一）計算假定

首先設定下列力學模型的假設：

（1）土體表面以及地表下各土層都處與均質且水平的層狀分布；

（2）初始應力只有自重;

（3）用Mohr-Coulomb屈服準則進行計算；

（4）不考慮地下水對地表沉降造成的問題；

（5）在盾構掘進過程中假設每一步的步長推進的長度和管片的寬度一樣為3.5m。

（二）網(wǎng)格劃分

由于本模型的尺寸非常大，只選取了交叉部分作為參考對象。地下隧道中應力以及應變隨著盾構掘進進程不斷改變,真正影響隧道的范圍是距隧道中心點的3到6倍開挖半徑的范圍。本次的數(shù)值模擬計算模型寬130m，高70m，縱向長度為140m（每環(huán)管片幅寬1.5m）,模型X方向（橫向）范圍為隧道外徑的四倍大小[2]，模型底部距五號線隧道中心35m。為了簡化模型大小，減小計算步驟計算，所以設每步開挖3.5m。土體模型的節(jié)點點數(shù)為128,872，單元總數(shù)為80000。模型網(wǎng)格劃分如圖2所示。

三、地表沉降分析

由于在盾構掘進過程中施工擾動會導致隧道周邊原有的土層產生應力重分布，為了防止由于應力重分布引起土體坍塌或是其他不利于工程的情況出現(xiàn)，在盾構機開挖后要立刻在盾構機的末端進行注漿加固對土體進行支撐，這樣會及時調整由于地層損失引起的地表變形[3]。

為進一步分析近接交叉隧道盾構施工對周邊地表沉降的影響規(guī)律，下文采用數(shù)值分析，模擬相同施工環(huán)境下幾種不同屬性的注漿引起的地表沉降。

圖2 隧道位置模型

首先考慮的是不進行盾尾注漿，由于盾構施工后，在盾構機行駛的過程產生的應力應變重分布會導致土層發(fā)生塌落，可以假定這種塌落的土層直接充滿盾構機末端的空隙,好比盾構機前方土匯聚成了一個向隧道內部的位移的趨勢,位移的范圍和大小相當于盾構施工后尾部的空隙。

另外一種情況就是不考慮由注漿由液體形態(tài)轉化為固體行形態(tài)的過程，就把注漿體看作均質的，連續(xù)的超高強度的固化物。然而在通過實際的盾構掘進過程中,盾構機末端的注漿量的多少以及組成注漿體的材料等，對盾構掘進區(qū)隧道周邊土體沉降會產生比較大的影響。所以在對盾構機末端進行注漿時需要一種厚度差不多，屬性相近的具有平均意義的等代層來替換成這種由水泥沙子等粗細骨料組成的注漿體[4]。

組成等代層的是像碎石、砂子等粗細骨料的混合體,因此所假設的等代層的材料性質與其土體性質、注漿材料以及注漿壓力都有著聯(lián)系,如果把等代層當成是彈性材料,那么等代層的材料性質就應該具有厚度、泊松比、彈性模量等力學性質。其中,彈性模量反應了的漿液性能，其選擇非常關鍵。

由于交叉隧道位于第三層土 （彈性模量40000-100000KN/m3），所以等代層的彈性模量應該在土層與水泥之間，取值的大小應該與組成兩者的材料的多少有關。使用不同彈性模量和泊松比的等代層來代替注漿進行計算出來的最大沉降值也就不同，所以假設兩種情況：一種是E=2GPa且泊松比為0.3；另一種是：E=20GPa，同時泊松比等于0.3。

（一）橫向位移

圖3 地表橫向沉降位移

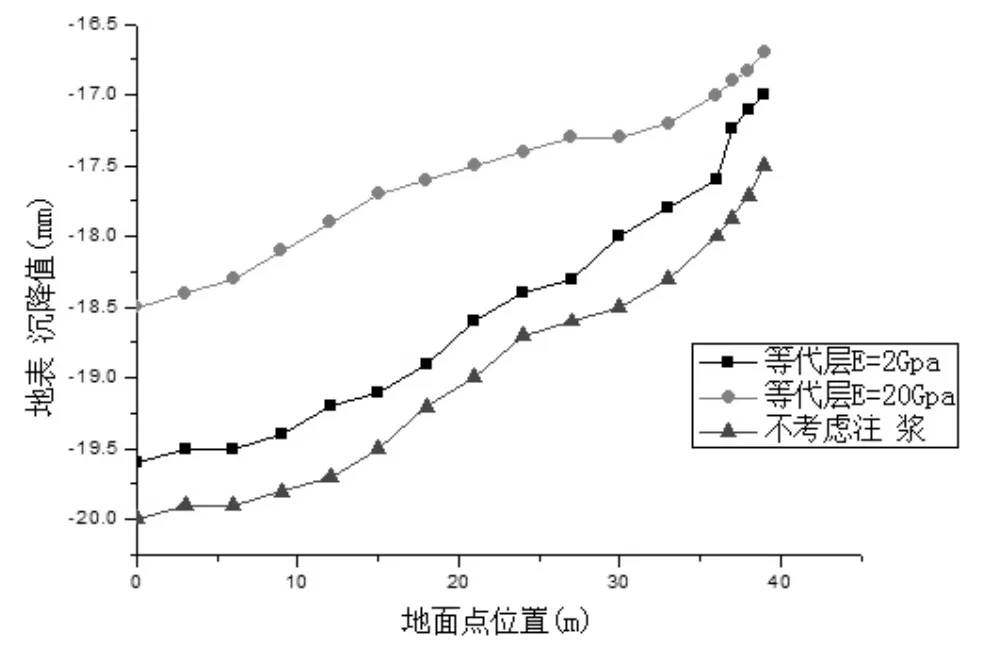
圖4 一號線右線隧道中心線地表縱向沉降曲線

圖5 一號線左線隧道中心線地表沉降曲線

通過觀察圖4可以找出如下規(guī)律:

當?shù)却鷮釉贓=2GPa，泊松比為0.3；等代層在E=20GPa，泊松比為0.35以及沒有考慮注漿的情況下，三者的位移曲線形狀十分相似，但是地表橫向沉降位移量是不相同的，當E=20GPa時最大沉降量15.1mm,而不考慮注漿時最大沉降量為27.5mm。彈性模量及泊松比反應的是注漿剛度大小，所以說明等代層剛度大小對于地表的橫向位移有很大影響，注漿剛度越大，地表沉降數(shù)值就越小。

（二）縱向位移

通過觀察圖4至圖5中地鐵一號線左線及右線中心線地表沉降數(shù)值發(fā)現(xiàn)如下規(guī)律:

1.觀察圖5當沒有考慮注漿時一號線右線的最大沉降接近20mm,當取等代層彈性模量為2Gpa且泊松比為0.3時，最大沉降由20mm縮小到19.35mm；當取彈性模量為20Gpa且泊松比為0.35時，最大沉降緊接著隨之縮小，一號線右線最大沉降值約18.5mm。

2.圖6顯示，當一號線左線中心線在沒有進行注漿的時候最大沉降接近20.5mm，選擇彈性模量為2Gpa同時泊松比為0.3的等代層時左線中心線的最大沉降縮小了0.25mm,變成了20.25mm。最后取強度最大的等代層（彈性模量為20GPa，泊松比為0.35）時，一號線左線最大沉降進一步縮小到約18.90mm。

通過對上面兩個圖即一號線左右中心線的最大沉降觀察可以發(fā)現(xiàn)，隨著等代層剛度的增加，地表最大沉降數(shù)值在不斷縮小，因此在同樣的盾構掘進狀態(tài)下，可以通過對盾構機尾部使用高強度的注漿，來穩(wěn)定土層并且縮小地表沉降的數(shù)值。

（三）等代層厚度

地表沉降最大值與注漿量之間關系密切，文獻[5]從控制地表沉降的角度結合現(xiàn)場實測數(shù)據(jù)提出了最佳注漿量的確定方法。為反映近接相交隧道注漿量對地表沉降的影響，本文通過改變等代層的厚度反映盾尾不同注漿量和盾尾空隙情況，通過數(shù)值模擬，對盾構施工不同的等代層厚度下的地表沉降結果進行比較分析。

本文選取了3組厚度分別為8cm、12cm、20cm的等代層厚度進行數(shù)值模擬計算。考慮到普通粉質粘土的彈性模量介于土體和混凝土之間，在數(shù)值模擬中設置粉質粘土的彈性模量E=1.43×108pa。

結合數(shù)值模擬計算不同的等代層厚度下地表沉降值及地表沉降曲線（圖6）發(fā)現(xiàn)，當?shù)却鷮雍穸葹?cm、12cm、20cm時地表最大沉降值為 26.8mm、22.8mm、15.1mm。模擬數(shù)據(jù)表明等代層厚度與地表最大沉降呈反比，地表最大沉降值隨等代層厚度的增大而減小。

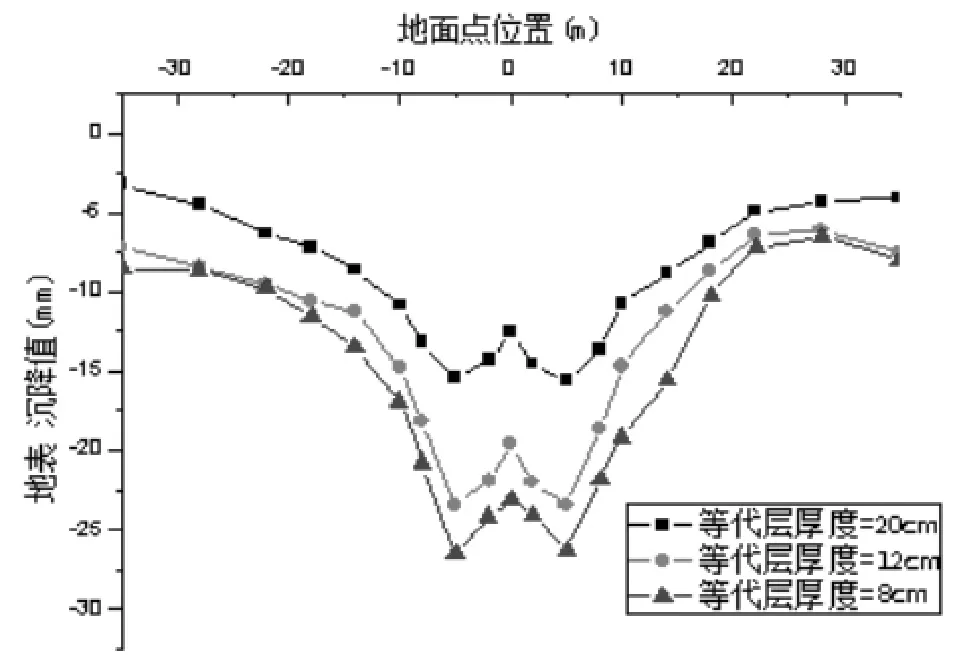
圖6 等代層厚度影響地表沉降圖示

四、監(jiān)測結果與midas比較分析

交叉隧道通過的土為第三層粘土我們假設掘進中洞室覆土為10m厚，洞室掘進的半徑為6米，土層粘聚力51KPa，內摩擦角為16度，取1號線右線與5號號線左線中間斷面，相應埋深為：8.8m～29.7m。

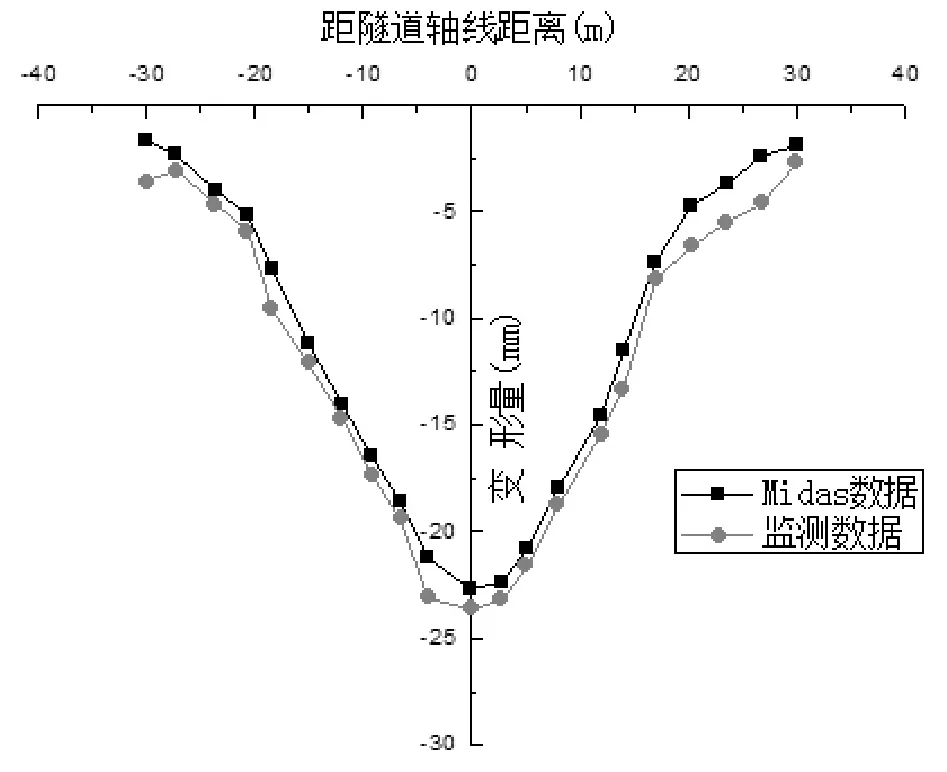
圖7 監(jiān)測數(shù)據(jù)與midas數(shù)據(jù)比較

從圖7中可以看出模擬數(shù)據(jù)基本上符合正態(tài)分布。實測數(shù)據(jù)有若干個測點的數(shù)值發(fā)生了跳躍，這與實際的地質條件和操作環(huán)境有很大的關系，有限元軟件可以通過改變模型中材料參數(shù)的方法準確反映不同地質條件和施工方法造成的地層移動。

五、結論

本文以合肥高鐵南站一號線與五號線交叉隧道施工為背景，運用數(shù)值模擬方法研究交叉隧道施工在注漿強度不同的情況下影響地表沉降的規(guī)律。通過研究得出以下結論：

1.彈性模量及泊松比反應的是注漿剛度大小，所以說明等代層剛度大小對于地表的橫向位移有很大影響，注漿剛度越大，地表沉降數(shù)值就越小。

2.在相同施工環(huán)境下，對于盾構機末端注漿強度的提高可以縮小地表沉降。所以在盾構掘進過程中可以通過加強注漿強度來減小一定的地表沉降。

3.等代層厚度與地表最大沉降呈負相關關系，因此注漿量的提高對于沉降的減小也是很有利的。