基于多目標優化與強化學習的空戰機動決策

杜海文, 崔明朗, 韓統, 魏政磊, 唐傳林, 田野

(1. 空軍工程大學航空工程學院， 西安 710038； 2. 94782部隊， 杭州 310004； 3. 福州大學物理與信息工程學院， 福州 350108)

隨著無人機技術的不斷發展，無人作戰飛行器(UCAV)的作用與地位也在不斷升高，在戰場上的意義越來越重要[1]；由于不必考慮人身體條件限制，UCAV可以完全發揮出飛行器的性能，做出有人機難以做出的大過載機動，可以預見UCAV必將成為未來空中戰場的主角。而要實現高強度的空中對抗，UCAV必須脫離地面控制，具備自主空戰的能力，本文結合傳統優化模型以及機器學習方法，建立了基于多目標優化的機動決策模型，用于解決UCAV自主空戰時的機動決策問題。

關于空戰機動決策問題有很多研究成果(包含有人機與無人機)，總的來說大致可以分為3類：①基于各類基本戰術動作庫的機動決策，文獻[2]最早對建立機動動作庫進行了系統的研究和總結，文獻[3-4]分別就機動動作庫的設計、控制應用以及基于動作庫的機動動作識別等問題進行了研究，詳細闡述了基于動作庫的機動決策中存在的各類問題。②基于優化方法的機動決策，該類方法的共同點在于通過各類態勢評估方法將機動決策問題轉化為標準的優化模型，文獻[5-6]基于各類不同的智能算法來求解優化模型，文獻[7]基于各類態勢分析方法建立了隱馬爾可夫模型，并使用維比特算法進行求解。③基于機器學習方法的機動決策，機器學習方法研究在近年得到了極大的發展，采用各類機器學習方法研究機動決策也越來越多，文獻[8]應用深度置信網絡來進行態勢評估，文獻[9]采用了強化學習方法研究空戰智能決策。

然而，以上方法在處理無人機空戰機動決策時都存在一些弊端：機器學習方法在處理類似對抗博弈問題時效果很好，但不同于有人機的空戰決策，無人機空戰基本不存在有學習價值的樣本；而各種基于動作庫的方法雖然是建立在大量空戰經驗之上，但靈活性較差，且現在的空戰經驗都是有人機的經驗，無法確定其用在無人機上是否可靠。相比之下，傳統的優化方法原理是基于對態勢分析的尋優，反而可以根據不同的飛行器性能和空戰環境得出實時性與靈活度都較強的決策，但是傳統優化方法在整合不同態勢參數時缺少嚴謹的方法，且其決策結果隨著模型的確立就已經確定下來，無法體現出對抗博弈的思想。基于上述分析，本文依然使用優化模型作為決策的核心思想，采用多目標優化方法取代單目標優化，并通過強化學習方法建立輔助決策網絡，建立了具備實時對抗性的無人機空戰機動決策模型。

1 機動決策模型

1.1 UCAV運動模型

在對UCAV近距空戰進行機動決策與仿真時，采用三自由度質點模型描述UCAV的運動狀態，模型參數定義如圖1所示。

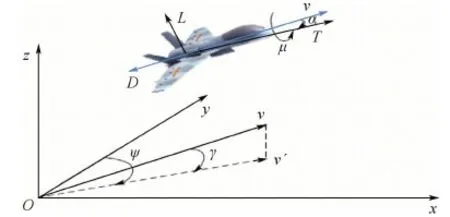
圖1 UCAV三自由度質點模型Fig.1 UCAV three-degree-of-freedom particle model

1.1.1 模型假設

對建立UCAV運動、動力學模型作如下假設：

1) 假設UCAV為一個剛體。

2) 假設地球為慣性坐標系(將地面坐標系看作慣性坐標，忽略地球自轉及公轉影響)。

3) 忽略地球曲率。

1.1.2 UCAV質點模型

在考察UCAV運動時，將UCAV視為質點。在慣性坐標系下，其質點運動方程為

(1)

相同慣性坐標系下，UCAV的質點動力學方程為

(2)

式中：vu為速度；γ為航跡傾角；ψ為航向角；μ為滾轉角；α為迎角；m為質量；T為發動機推力；D為空氣阻力；L為升力；g為重力加速度。

飛行過程中，UCAV所受升力L與空氣阻力D計算公式如下：

(3)

式中：ρ為空氣密度；S為UCAV參考橫截面積；CL和CD分別為升力和阻力系數。

UCAV發動機推力T計算公式如下：

T=δTmax

(4)

式中：Tmax為發動機最大推力；δ為油門，取值范圍為[0,1]。

在控制量的選擇上，仿照有人機中飛行員的駕駛方式，采用迎角α、油門δ、滾轉角μ三個控制量來控制UCAV進行機動。

1.2 多目標優化方法

基于優化方法的機動決策模型具有較高的決策效率與良好的實時性，但在尋優過程中需要對多個目標參數進行合并，這樣的合并過程往往使用層次分析法、專家打分法等主觀性較強的方法來確定權值，缺少嚴格的證明過程，其決策結果難以使人信服。

事實上，在不同的空戰環境下，對于各個態勢參數的需求程度也是不同的，所以將不同態勢參數加權求和后進行優化的方法本身就具有很大的局限性。為了避免這種局限性，本文結合多目標優化思想，建立了多目標優化機動決策模型。

1.2.1 多目標優化思想

首先簡要介紹一些多目標優化問題中的概念，在多目標優化中，采用Pareto支配[10]關系來判斷解的優劣程度，Pareto支配關系的定義如下。

定義1對于可行域內任意2個解x1與x2，假設在最小化問題f(f1,f2,…,fk)中，當且僅當式(5)成立時稱x1對x2形成Pareto支配：

[?i∈{1,2,…,k},fi(x1)≥fi(x2)]∩

[?i∈{1,2,…,k},fi(x1)≥fi(x2)]

(5)

x1支配x2表示解x1優于解x2，一般記作x1?x2。

由定義1可知，求解多目標優化問題的本質就是在全部可行解中找到所有不被任何一個其他可行解所支配的解的集合。將這個集合稱之為多目標優化問題的Pareto邊界，具體定義如下。

定義2設多目標優化問題f的可行解集為X，則其Pareto邊界為

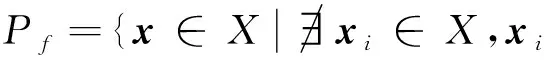
(6)

多目標優化的目的就是求出優化問題的Pareto邊界。

1.2.2 優化目標

使用優化模型必然需要構建優化目標參數，采用速度、高度、距離、角度[11-12]4個量作為優化目標是最為常用的方法之一，但這些量的具體戰術意義還不夠明確，本文將基于空戰實際將這些參量進行耦合后提出了如下優化目標參數。

1) 基于武器攻擊區的威脅參數

空戰的最終目的就是擊落敵方與保護己方，進行機動也正是為了使己方構成武器發射條件和避免使對方構成武器發射條件，故本文基于機載武器攻擊區的概念，結合與之相關的角度、距離等常規評估參數，提出了一種新的威脅參數ηA作為一個優化目標，參數模型以雙方攜帶彈藥類型為基礎，具體定義如下。

① 常規條件下。制導武器一般以空空導彈為主，現在的空空導彈的攻擊區大致如圖2所示。

假設圖2中攻擊區為我機攜帶的第i枚導彈的攻擊區，則該型導彈對敵機威脅參數為

(7)

式中：Rg為該導彈沿視線角αu方向上的最遠攻擊距離，由于部分導彈不具備全向打擊能力，故若在當前αu下Rg為0，則定義此刻ηai=0。

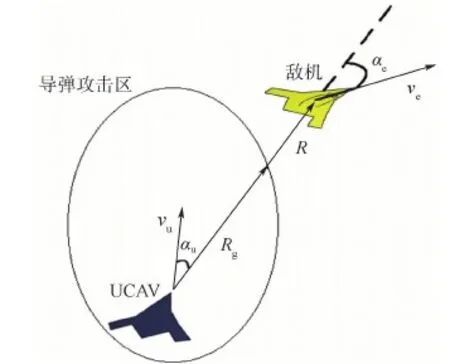
圖2 態勢參數定義Fig.2 Definition of situation parameters

根據上述方法計算出我機攜帶所有空空導彈對敵機威脅參數(ηa1,ηa2,…,ηan)后，取其中的最大值ηamax，即為我機當前對敵機的威脅參數ηa；采用相同方法計算出敵機對我機威脅參數后，取兩者之差即為總威脅參數值ηA：

ηA=ηa(ucav)-ηa(enemy)

(8)

② 僅使用非制導武器時。空對空作戰非制導武器一般指航炮，由于航炮的發射條件比較苛刻，一般只在形成尾追時才能構成發射條件，故直接使用雙方角度參數與距離參數進行耦合來定義其態勢參數：

(9)

式中：Ra為航炮射程。

2) 能量參數

能量理論[13]是近期提出的一種空戰機動理論，該理論的核心在于：在空戰中首先尋求獲得能量上的優勢，然后將能量優勢轉化為態勢上的優勢。能量理論隨著飛機性能的提升愈發受到重視，現在的飛機性能可以支持完成各種大過載機動、過失速機動等非常規動作，這使得飛機可以有更多方式扭轉不利的態勢。即使在常規的機動對抗中，能量也是一個不可忽略的條件，因為所有機動動作都是以消耗能量為前提，高能量就意味著更多的機會與選擇。故本文設置能量參數ηW作為一個優化目標，計算公式如下：

(10)

式中：Wp和Wk分別為重力勢能與動能；Wst為能量標準化參數；mu為我方UCAV質量。

1.2.3 多目標優化機動決策模型

決策模型結構如圖3所示。

目前有很多種多目標算法可供使用，由于上述模型復雜度不高且機動決策對實時性有較高要求，考慮到灰狼算法在處理維數較低問題時收斂速度快，本文在仿真時采用多目標灰狼算法(MOGWO)[14-15]。

事實上，多目標優化模型具有良好的可拓展性，在實際應用時，可以根據實際空戰環境在以上2種優化目標的基礎上添加其他新的優化目標(如雷達性能、電子戰等)，添加時只需將新的目標參數模型加入原優化目標集即可，不需要對決策模型中的其他結構進行任何變化。

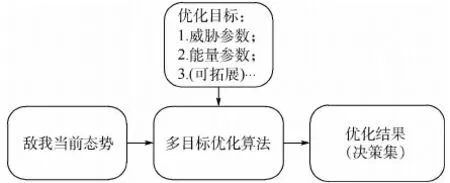
圖3 多目標優化機動決策模型結構Fig.3 Structure of multi-objective optimization model for maneuver decision

1.3 基于強化學習方法的輔助決策

1.2節提出了多目標優化思想并建立了優化參數的模型，但多目標優化模型仍存在以下缺點：

1) 多目標優化的結果是一個決策集，并沒有給出從決策集中的選擇具體決策的方法，如果不采用其他輔助決策方法，則只能從決策集中隨機選取決策。

2) 多目標優化的本質依然是優化模型，未體現出空戰博弈的思想。

強化學習方法[16]在處理類似的對抗博弈決策中取得了很大成果，但由于無人機空戰決策問題的復雜度太高而難以實現。然而，如果在多目標優化的基礎上進行強化學習，強化學習任務的探索空間將大大減少，故本文以多目標優化為決策基礎，使用強化學習方法訓練評價網絡，用于對決策集中的決策進行評價與選擇，從而解決上述2點不足。

1.3.1 蒙特卡羅強化學習

強化學習任務通常用馬爾可夫決策過程(Markov Decision Process，MDP)來描述，任務對應了四元組E=，St為狀態空間，是機器所感知到的環境描述的集合,Ac為系統能夠采取的行為的集合,Pr指定了不同環境下采用各種行為的概率，用以在探索過程中為行為選擇提供參考,Re指定了獎賞，通過反饋來調整Pr中的概率。

雖然對于空戰中態勢評估的研究已較為完善，但考慮到空戰過程中機動動作往往是一系列的連續動作，即在完整的機動決策中，并非每一時刻都是為了追求最優態勢。所以要設置符合要求的獎賞函數并不容易，而蒙特卡羅方法可以解決這個問題。

蒙特卡羅強化學習[17]的思路是采用多次“采樣”求平均獎賞的方式來近似對行為的評價，即系統從起始狀態下開始探索環境直至結束，將整個過程的獎賞作為過程中經歷的每一個狀態st的一次累積獎賞，在多次采樣后，對每一個狀態st的累積獎賞取均值得到其獎賞值re。

就效率而言，蒙特卡羅強化學習比其他強化學習方法相去甚遠，在實踐中對蒙特卡羅方法的應用也不是很廣泛，但本文模型的決策核心還是多目標優化，強化學習任務只需對多目標優化的決策結果進行評價與選擇，即強化學習的行為空間A為一個已經經過篩選的較小空間，故收斂速度必然大大提升，從而使蒙特卡羅方法具備了可行性。

1.3.2 基于神經網絡的值函數近似

初始的強化學習方法都是針對離散的狀態-動作空間來進行的，但對于空戰而言，其狀態空間與動作空間都是連續的高維空間，進行離散化處理顯然不是合適的方法。在類似的高維連續空間強化學習中，往往采用值函數近似的方法來進行連續空間的強化學習。

值函數近似[18]指的是通過一個函數φ建立從狀態St到狀態獎賞值的映射:φ:St→Re。考慮到空戰決策問題的復雜性，最終的近似函數必然是復雜非線性函數，而神經網絡在擬合復雜非線性函數時具備較好的性能， Hornik等[19]在1989年就證明了只需一個隱層的BP神經網絡可以逼近任何閉區間的連續函數，故本文將訓練一個三層的BP神經網絡來擬合值函數，用以對多目標決策集進行評價。隱層節點數將依照以下經驗公式進行設計：

(11)

式中：lno為隱層節點數；nno和mno分別為輸入和輸出節點數；ano為1～10之間的調節常數。

結合對輔助決策網絡功能的需求，網絡具體設置如下：

1) 將空戰態勢(即狀態量)作為輸入層，利用si{R,αu,αe,Δh,Δv}5個參數來描述空戰態勢，即網絡輸入層節點數為5，Δh為兩機高度差，Δv為速度差。

2) 網絡輸出為對輸入態勢下我機獲勝期望的預測值ν([0,1]之間的數，ν值越大代表獲勝期望越大)，輸出層節點數為1。

3) 神經網絡訓練采用LM(Levenberg-Marquardt)方法，其中BP誤差計算類似于時序差分(TD)方法[20]誤差計算公式，但由于模型采用蒙特卡羅方法，只能使用每次仿真結果作為本次仿真所經歷狀態的統一獎賞值，具體計算公式如下：

(12)

式中：αRL為學習率，一般根據訓練次數確定；γRL為折扣率，本文取γRL=0.4；r為獎賞值，r值由仿真結果rend給出，rend取值為0、0.5或1(對應失敗、平局或勝利)；n為本次仿真經歷的總步數；i為當前狀態步數。

4) 結合隱層節點數經驗公式，通過實際仿真效果，選擇隱層節點數為12。

1.3.3 輔助決策模型

輔助決策網絡的強化學習模型訓練步驟如下：

步驟1初始化輔助決策網絡。

步驟2隨機產生敵我雙方初始位置狀態，開始仿真模擬。

步驟3記錄下當前敵我態勢關系sii，由多目標決策模型得出決策集(敵機可以采用與我機相同策略進行機動，或根據實際需求預先設置其軌跡)。

步驟4預測每種決策后敵我態勢關系，進而通過輔助決策網絡得出對應的獲勝期望{ν1,ν2,…,νn}。

步驟5從決策集中隨機選取出最終執行的決策，每種決策的被選取概率為

(13)

步驟6執行決策后判斷是否達到空戰結束條件，若未達到，返回步驟3；若已達到，進入步驟7。

步驟7對本次仿真所經歷的所有狀態si，通過式(12)計算BP誤差返回輔助決策網絡用于網絡更新。

步驟8判斷是否達到最大訓練次數，若未達到，返回步驟2。

注意：訓練過程中，若敵機采用相同的決策模型，則雙方數據均可通過步驟7中的網絡更新；若敵機采用預先設置好的其他機動方法，則只有我方數據可用于網絡更新。

1.4 機動決策模型整體框架

結合1.2節和1.3節描述的多目標決策模型與輔助決策網絡，機動決策模型整體框架如圖4所示。

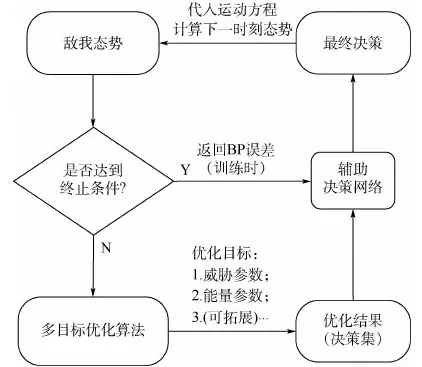
圖4 機動決策模型結構Fig.4 Structure of maneuvering decision model

2 仿真實驗

由于本文機動決策涉及模型較多，故在仿真時將針對各個模型予以驗證，仿真環境及參數設置如下。

仿真時，敵我飛行器采用相同的參數，質量m=14 680 kg，參考截面積S=49.24 m2，高度限制為h∈[1,12] km，速度限制為v∈[80,400] m/s，迎角限制為α∈[-10°,30°]；發動機采用F-4渦噴發動機數據[21]，其最大推力采用式(14)擬合：

(14)

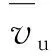
升力系數和阻力系數采用式(15)擬合[22]：

(15)

考慮到本文未針對探測能力設置優化函數，故訓練時設置雙方均只使用航炮進行近距空戰(近距格斗時電子戰作用較小，但對機動決策模型有較高要求)，所有仿真中決策步長為1 s；訓練過程中，判定相互脫離距離為15 km；攻擊條件設置為αu∈[-20°,20°]且R<2.5 km(參數定義見圖2)，滿足攻擊條件3 s視為進行有效攻擊；任意一方進行有效攻擊或雙方脫離則仿真結束。

仿真實驗在Matlab 2013a下進行，運行環境為Inter(R)Core(TM)i5-2310處理器，3.40 GB內存。

2.1 多目標優化可行性驗證

1) 時間可行性

由于輔助網絡在決策時的耗時遠小于多目標優化，故首先驗證多目標優化方法的實時性，本文采用MOGWO作為求解模型的算法，隨機產生100組敵我態勢并使用算法尋優，仿真時灰狼種群與外部種群數均設置為30，迭代次數為3次。

采用MATLAB自帶的計時功能記錄了100次決策時間，決策平均時長t=0.286 541 s，遠小于決策步長1 s，故決策模型具有良好的實時性。

為了展示尋優效果，圖5記錄了上述實驗過程中的一次尋優的結果，其中紅點為算法尋優結果，藍點為可行域的大致范圍(通過窮舉法得出)，可以看出MOGWO可以在上述條件下找到基本完整、均勻的Pareto邊界。

2) 決策可行性

驗證通過多目標優化方法決策集的可行性，仿真時隨機產生100組初始態勢，敵機按初始態勢做勻速直線運動，我機在不使用輔助網絡的情況下進行機動，即決策時從多目標優化的決策集中按等概率隨機選取最終決策，每組仿真模擬75 s的空戰情形(若在75 s內達到結束條件則提前結束仿真)。

圖6記錄了100組仿真中我方優化目標函數在每秒的平均值(提前結束的組自結束起至75 s的目標函數值均按結束時的目標函數值記錄)。

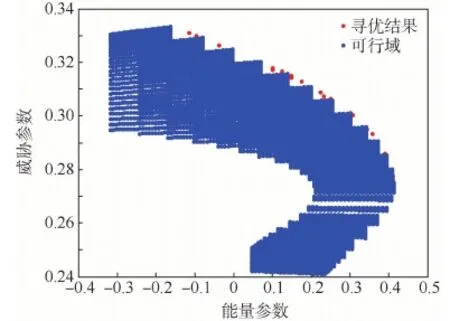
圖5 算法尋優效果Fig.5 Algorithm optimization result

通過圖6可知，我機態勢在多目標優化方法的決策下明顯優于初始時刻，且過程中威脅參數基本始終保持遞增，而能量參數僅出現一次大幅下降后同樣保持遞增(初始的大幅機動必然會導致能量損失)。

為了更直觀地展示多目標優化的性能，圖7記錄了在相同初始條件下進行2次重復實驗的結果(其中紅色為我方軌跡，藍色為敵方軌跡)，在初始條件相同的2次仿真中，我方做出了2次不同但均有效的機動。

圖6 目標函數變化趨勢Fig.6 Change trend of objective function

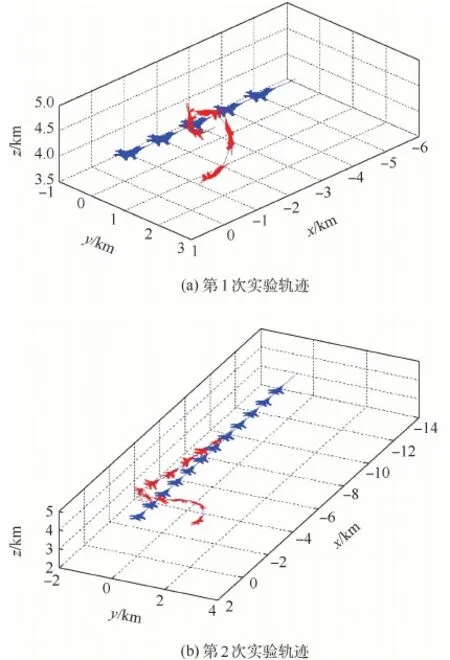
圖7 仿真軌跡(相同初始條件)Fig.7 Simulation trajectory map (the same initial conditions)

2.2 輔助決策模型有效性驗證

為了驗證輔助決策模型的有效性，按照1.3節中的強化學習模型訓練輔助決策網絡，訓練總次數為20 000次，訓練中雙方戰機采用相同的決策模型。

為了實時反映訓練效果，每進行200次訓練就對輔助模型性能進行一次檢測；檢測方法類似2.1節中驗證決策可行性的實驗方法，但我機在決策時采用輔助網絡(即使用1.4節決策模型)，為了節省時間，每次檢測重復200次且僅記錄最終結果，測試結果如圖8所示。

由測試結果可以看出，隨著訓練次數的增加，我方的獲勝次數明顯得到了提升，獲勝概率從25%左右提升到50%左右，說明在輔助網絡的幫助下，模型可以給出更為有效的決策。此外，由于雙方初始位置為隨機產生，每次測試中必然會出現少數極端不利的初始條件，故測試結果中一直存在一定的失敗次數。

為了進一步體現輔助網絡的效果，使用帶輔助網絡的決策模型與僅使用多目標優化方法的決策模型進行對抗仿真(將僅使用優化方法的一方視為敵機)，為了使仿真結果更具代表性，初始態勢將在一定范圍內隨機產生，具體約束條件如下。

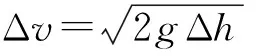
1) 初始有利(αe+αu∈[0°,90°])。

2) 初始均勢(αe+αu∈(90°,270°))。

3) 初始不利(αe+αu∈[270°,360°])。

在3種情形下各進行100次對抗仿真，結果如表1所示。

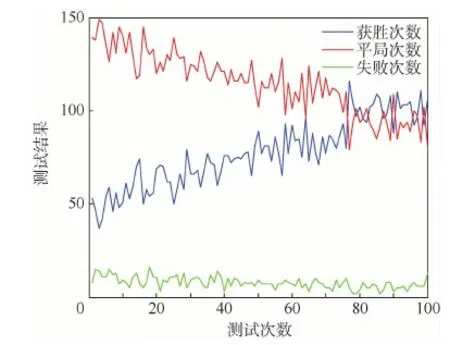
圖8 輔助決策模型性能測試結果Fig.8 Test results of auxiliary decision model’s performance

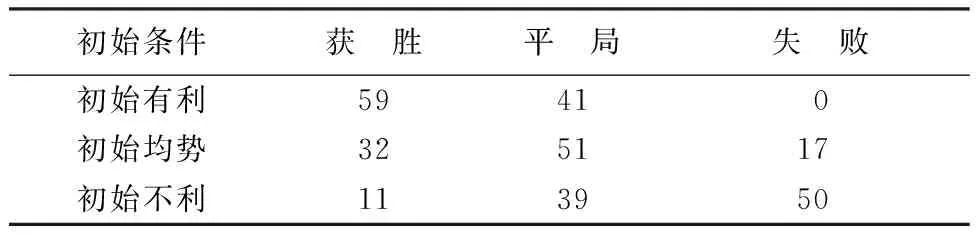
初始條件獲 勝平 局失 敗初始有利59410初始均勢325117初始不利113950

通過仿真結果可知，在使用了輔助網絡后，決策模型可以做出更高效、更具有對抗性的決策，平均獲勝概率提升了11.7%。

2.3 機動決策模型性能仿真

為了體現本文機動決策模型的性能，設置了2種情形下的空戰環境，其中敵機采用的機動均為經典的戰術動作，我機采用基于多目標優化的機動決策模型，輔助決策網絡采用2.2節仿真實驗中訓練出來的神經網絡。

1) 情形1中，我機初始處于較優的態勢環境，敵機采用“S型”機動進行規避，仿真結果如圖9所示。圖中紅色為我方，藍色為敵方，軌跡上的飛機模型表示飛機當前姿態，相鄰2個模型時間間隔為4 s。

圖10分別給出了空戰過程中雙方攻擊判定條件(視線角與距離，我機視線角αu的定義見圖2，敵機視線角即為π-αe)以及我方決策得出的控制量的實時變化情況。

通過仿真數據可知，初始條件下我方占據較大優勢，決策模型根據敵方位置調整我方視線角以形成攻擊條件；但由于我方速度較大且敵方采取“S型”機動，在20 s左右我方基本完成轉向后存在超越敵方的風險；決策模型采用了類似異面機動的原理，先適當俯沖再拉起機頭以避免戰機沖前，在拉起機頭的過程中再次調整視線角；從第44 s開始對敵方形成有效攻擊條件并保持，47 s時達到仿真結束條件，我方獲勝。

情形2中，我方初始處于不利條件，但由于距離敵機較遠，故存在機動規避的空間；敵機采用“純跟蹤”的方法試圖接近并攻擊我方，仿真結果如圖11所示(圖中標記同情形1)。

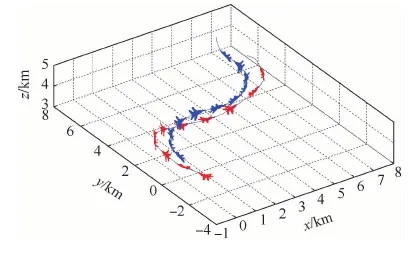
圖9 仿真軌跡(初始有利)Fig.9 Simulation trajectory map (favorable initial conditions)

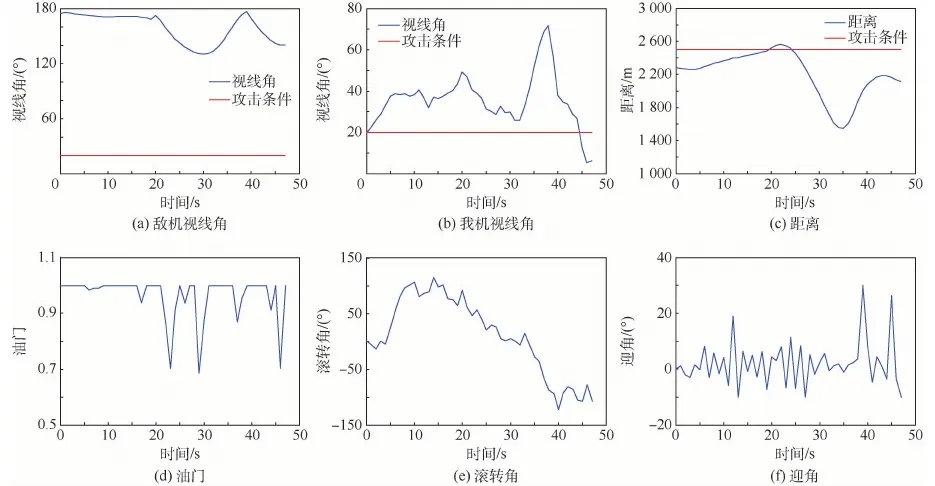
圖10 態勢關系與控制量(初始有利)Fig.10 Situation relationship and control quantity (favorable initial conditions)

圖12分別給出了空戰過程中雙方攻擊判定條件(視線角與距離)以及我方決策得出的控制量的實時變化情況。

通過仿真數據可知，初始我方處于不利態勢，決策模型選擇在向右機動規避的同時拉起機頭；爬升的過程必然會損失動能，故雙方距離逐漸縮小，15s左右時，敵方開始右轉以保持態勢優勢；由于此時我方速度較低，具有更小的轉彎半徑，決策模型選擇向右下方急轉接敵，并在第29 s搶先形成攻擊條件并保持，32 s時達到仿真結束條件，我方獲勝。

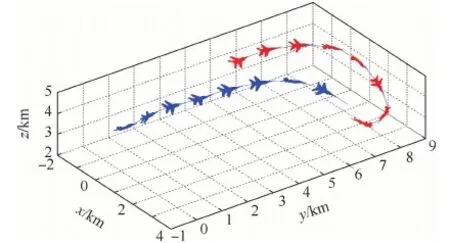
圖11 仿真軌跡(初始不利)Fig.11 Simulation trajectory map (adverse initial conditions)

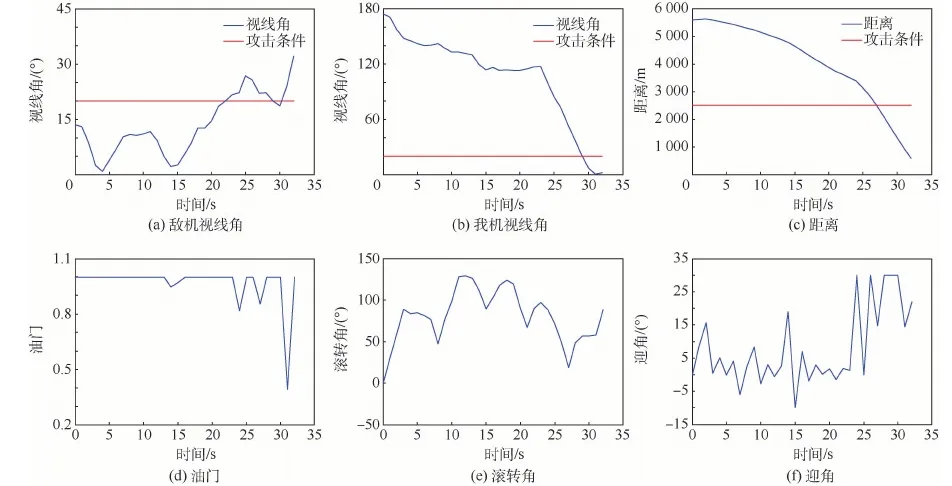
圖12 態勢關系與控制量(初始不利)Fig.12 Situation relationship and control quantity (adverse initial conditions)

3 結 論

本文提出了多目標優化與強化學習相結合的機動決策模型，模型融合了傳統優化方法與機器學習方法的優點：

1) 多目標優化方法解決了傳統優化方法中處理目標函數權重的問題，增加了決策模型的可信度和可拓展性。

2) 多目標優化方法繼承了傳統優化方法的優點，可以進行實時有效的機動決策。

3) 多目標優化的決策集直接給出了足夠的可執行決策，極大程度上簡化了動作空間，使強化學習任務具備了可行性。

4) 通過強化學習建立輔助決策網絡，從而可以在多目標優化決策集中做出更好的選擇，彌補了優化方法在對抗、博弈問題上的不足。

由于本文重點在于結合傳統優化方法和機器學習方法，在設置優化目標時僅針對較為理想的仿真環境設置了2個目標，設置在復雜電磁環境下新的目標函數模型是下一步的改進方向。