激波誘導推力矢量噴管不同氣體噴注時的性能分析

王曉明， 劉輝， 韓龍柱， 袁修干

(1. 北京航空航天大學航空科學與工程學院, 北京 100083； 2. 中國航發商用航空發動機有限責任公司, 上海 200241； 3. 北京航空航天大學生物與醫學工程學院， 北京 100083； 4. 北京航空航天大學生物醫學工程高精尖創新中心， 北京 100083)

現代戰爭對飛行器的機動性要求越來越高。而推力矢量控制技術的應用可有效提高飛行器的機動性能，減小飛行阻力，提高隱身及生存能力，因此越發受到人們的重視。而傳統的機械式推力矢量控制技術系統復雜，質量大，響應時間長，基于減重增效的考慮，研究更高效的推力矢量發動機已成為未來飛行器性能提高的關鍵技術之一[1-3]。激波誘導推力矢量控制技術是在噴管擴張段注入二次流體形成激波，改變噴管出口氣流的方向，來實現推力矢量控制。該技術系統結構簡單，響應時間極短，是一種理想的技術方案[4-7]。

國外的激波誘導推力矢量控制技術研究最初始于20世紀60年代，主要針對火箭發動機開展了一系列燃氣和液體二次噴射矢量控制的技術研究，其中液體二次噴射激波誘導推力矢量控制方案在一些戰術導彈上已成功應用[8]。從20世紀90年代開始，美國的NASA Langley實驗室開展了針對航空發動機的流體控制推力矢量控制技術的研究工作，取得了較大進展[5]。而國內相關領域研究開展于20世紀90年代末，理論和試驗研究資料相對匱乏，只局限于穩態條件下次流噴射角度、噴射位置等幾何因素對推力矢量性能影響規律的分析研究。

激波誘導推力矢量噴管的次流氣源可以從發動機燃燒室引氣，也可以由單獨的氣源供氣。因此，根據氣源的不同，次流的種類也不盡相同。而現有研究主要針對主流和次流為同種氣體的情況，本文則主要研究了不同工質次流氣體條件下噴管的推力矢量性能。通過對噴管內流場進行數值模擬，分析比較次流的滲透高度、噴管的矢量偏轉角和推力系數等參數，研究次流的分子質量對推力矢量性能的影響規律，從而選擇合適的次流氣體，提高矢量噴管的性能。

1 數值方法

噴管內流場為超聲速、可壓縮氣體，密度脈動不能忽略，因此Navier-Stokes方程中的湍流脈動項采用Favre提出的質量加權平均[9]。為使Favre平均Navier-Stokes方程封閉，Favre平均得出的雷諾擴散項和雷諾導熱項由梯度擴散假設封閉，其中湍流施密特數(Sc)和普朗特數(Pr)均設為0.9。雷諾應力項由Boussinesq假設封閉，湍流黏性由k-ωSST(Shear Stress Transport)湍流模型方程獲得[10]。

依據上述說明，笛卡兒坐標系下多組分守恒型控制方程的形式如下：

(1)

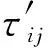
氣體守恒方程為

(2)

式中：p、ρ和T分別為氣體壓力、密度和溫度；R為理想氣體常數；Ms為各組分分子質量。

控制方程的無黏通量向量采用AUSM (Advection Upstream Splitting Method)格式的改進型ASUM+格式進行離散[11]：

(3)

式中：各變量符號說明參見文獻[11]。

通過對原始變量進行MUSCL (Monotone Upstream-centred Schemes for Conservation Laws)差值，可提高到二階精度[12]。黏性通量向量采用中心差分離散。時間推進采用LU-SGS (Low-Upper Symmetric Gauss-Seidel)隱式格式[13]。

2 程序驗證及算例

2.1 物理模型

將文獻[14]中的氮氣垂直噴入超聲速空氣流場的試驗結果來驗證程序的準確性。其試驗臺為500 mm×150 mm×150 mm的三維槽道，其結構平面圖如圖1所示。計算網格為318×69×69，在噴射口和壁面處局部加密。表1給出了主流場中的空氣參數和噴射入口處的氮氣參數[14]。

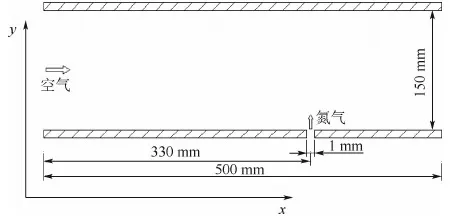
圖1 氮氣噴射試驗臺幾何構型Fig.1 Geometry configuration of nitrogen injection testbed

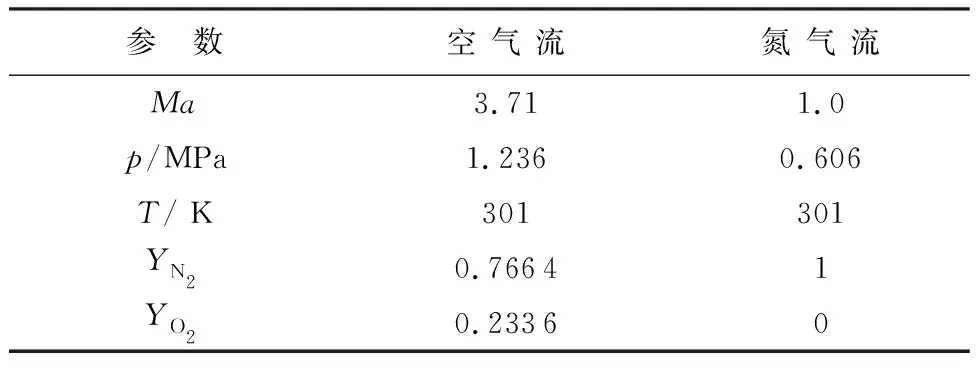
參 數空 氣 流氮 氣 流Ma3.711.0p/MPa1.2360.606T/ K301301YN20.76641YO20.23360

注：Ma—馬赫數；YN2—氮氣組分質量分數；YO2—氧氣組分質量分數。

2.2 計算結果

圖2為馬赫數等值線，圖3為噴射口附近區域的流線，x、y分別為空氣流入方向和氮氣注入方向。氮氣從噴射口欠膨脹噴出，超聲速氣流通過Prandtl-Meyer膨脹在噴射口外形成馬赫盤。由于噴射氣流與主流的交叉干擾作用，在噴射口上游區域形成弓形激波。弓形激波前流場壓力升高，致使壁面邊界層分離，進而形成了一個與弓形激波相交的分離激波。另外，在噴射口下游區域形成再壓縮激波。如圖2和圖3所示，干擾流場復雜的激波結構，馬赫盤和分離渦系結構都被數值方法很好的捕捉。

圖4為計算所得壁面壓力分布與試驗數據結果對比，p∞為空氣來流總壓，L為氮氣噴射孔中心線到入口的距離(即330 mm)。由圖4可見，計算結果與試驗數據吻合得很好，只是在噴射口下游計算所得壓力的峰值比試驗數據略低。

由上述分析可知，AUSM+格式和k-ωSST湍流模型能夠很好地模擬橫向噴流的流場結構，計算結果也與試驗數據吻合得很好，驗證了數值方法的可靠性，因此該方法可以應用到激波誘導推力矢量噴管不同氣體噴注時的性能分析研究。

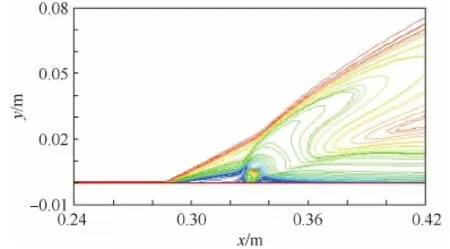
圖2 馬赫數等值線Fig.2 Mach number contour lines

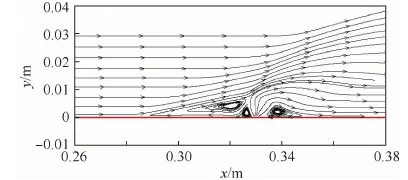
圖3 噴射口附近區域流線Fig.3 Streamlines near injection orifice

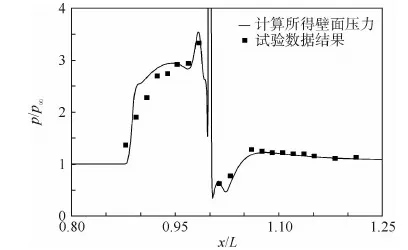
圖4 壁面壓力分布Fig.4 Wall pressure distribution

3 不同氣體噴注時性能分析

3.1 物理模型

噴管全長為78 mm，喉部直徑47 mm，噴管出口面積與喉部面積之比為2.09。由于在相同條件下，矩形注氣口的推力矢量性能優于同面積的圓形注氣口[15]，因此本模型在噴管擴張段開設周向角度40°，寬度3 mm的矩形注氣口。該注氣口的中心線距噴管入口的距離為噴管全長的0.75，次流方向與噴管軸線夾角為θ。由于幾何和流場結構的對稱性，沿對稱面選取一半作為研究對象。計算模型的網格如圖5所示。

噴管主流氣體為空氣，其中氮氣的質量分數為0.766 4，氧氣的質量分數為0.233 6，入口總壓為1 MPa和1.5 MPa，出口環境壓強為一個標準大氣壓，則主流落壓比(NPR)分別為10和15。次流氣體分別為He、N2和CO2氣體，其質量分數均為1，次流與主流總壓之比(SPR)分別為0.8和1.0，馬赫數為1，注氣角度θ分別為90°和105°，垂直和逆向主流噴入。主流和次流的總溫均為300 K。

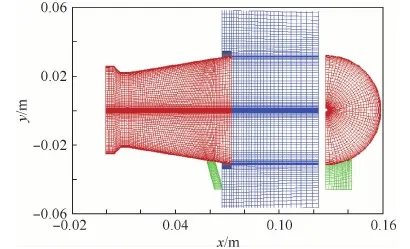
圖5 激波誘導推力矢量噴管計算網格Fig.5 Computational grid of shock thrust vector nozzle

3.2 評價標準

通過數值計算可得到噴管矢量偏轉角和推力系數作為推力矢量性能指標[16]。

矢量偏轉角度為

α=arctan(FN/FA)

(4)

式中：FN和FA分別為軸向力和側向力，可對噴管出口氣流積分得到。

推力系數為

CR,i=FR/(Fi,p+Fi,s)

(5)

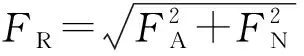
次流與主流質量流量比為

ω=Ws/Wp

(6)

式中：Ws和Wp分別為次流和主流的質量流量，可分別對噴管入口和次流入口積分得到。

3.3 計算結果

圖6～圖8所示的狀態:次流為He，NPR=10，SPR=1.0，θ=90°。圖6為He注入噴管流場后壓強分布。如圖6所示，激波誘導推力矢量噴管的流場結構與第2節中驗證模型的流場結構相似，二次流氣體噴入噴管擴張段，通過Prandtl-Meyer膨脹在噴射口外形成馬赫盤，由于次流的阻礙作用，在噴射口上游形成弓形激波，主流通過弓形激波流動方向發生偏轉，在噴管出口產生側向推力，實現矢量控制。

圖7為He注入噴管流場后在對稱面上質量分數等值線圖。如圖7所示，He注入噴管流場后滲透到一定高度，壓強逐漸降低，y方向速度逐漸減小，受噴管主流的推動作用，然后轉彎平行于噴管壁面流動。

圖6 流場壓強分布Fig.6 Pressure distribution of flow field

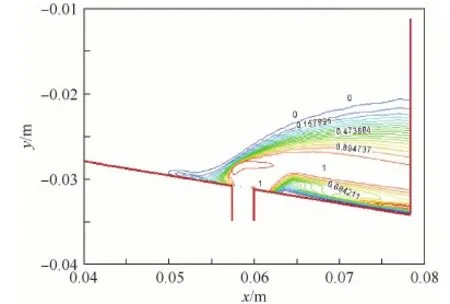
圖7 He質量分數等值線Fig.7 Mass fraction contour lines of helium

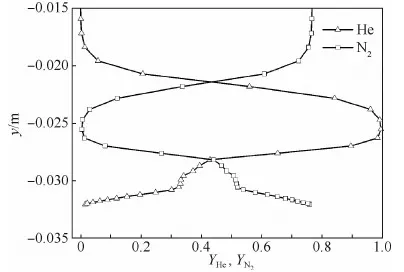
圖8 在對稱面x=0.066 m處He和N2的 質量分數沿y方向的分布Fig.8 Distribution of helium and nitrogen mass fraction along y direction at x=0.066 m on symmetry plane

圖8為對稱面上注氣口下游x=0.066 m處，He和噴管主流中的N2沿y方向的質量分數分布曲線。He在靠近壁面處質量分數很低，隨著高度的增加質量分數迅速變大，由于受回流渦結構的影響，在y為-0.031～-0.028之間，質量分數的增大趨勢變緩，之后隨高度增加質量分數又迅速增大，在y為-0.026～-0.023之間達到相對穩定的接近于1的值，然后隨著高度的增大又逐漸減小，直至為零。而主流中N2的質量分數變化與He正好相反。

圖9為NPR=10，SPR=1.0，θ=90°和105°時，He、N2和CO2氣體在對稱面x=0.066 m處沿y方向質量分數分布曲線。由圖9可知，3種氣體在此處的質量分數分布情況近似相同，在相同高度上，分子質量大的氣體質量分數略高。即分子質量越大，滲透高度越大。這說明，分子質量小的氣體由于滲透高度較低對主流的阻礙作用就會相應降低，從而減少推力損失。

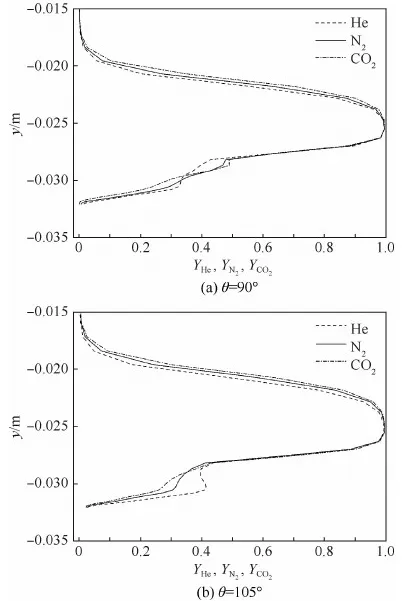
圖9 在對稱面x=0.066 m處不同次流氣體的 質量分數沿y方向的分布Fig.9 Distribution of mass fraction along y direction for different secondary flow gas at x=0.066 m on symmetry plane

表2為NPR=10，SPR=1.0時，不同注氣角度下矢量性能參數對比。由表2可知，在不同注氣角度下，矢量偏轉角均隨次流氣體分子質量的增大逐漸減小。推力系數則近似相等，隨分子質量的增大略微減小。分子質量越小，次流與主流的質量流量比ω越小。說明分子質量小的氣體在單位質量流量下產生的矢量偏轉角更大，而推力損失更小。

表3為SPR=1.0，注氣角度為105°時，不同NPR下矢量性能參數對比。由表3可知，在不同NPR下，矢量偏轉角均隨次流氣體分子質量的增大逐漸減小。另外，在NPR發生變化時，分子質量小的氣體其矢量偏轉角變化的程度更大。推力系數則近似相等，隨分子質量的增大略微減小。

表4為NPR=10，注氣角度為105°時，不同SPR下矢量性能參數對比。由表4可知，在不同SPR下，矢量偏轉角均隨次流氣體分子質量的增大逐漸減小。推力系數則近似相等。

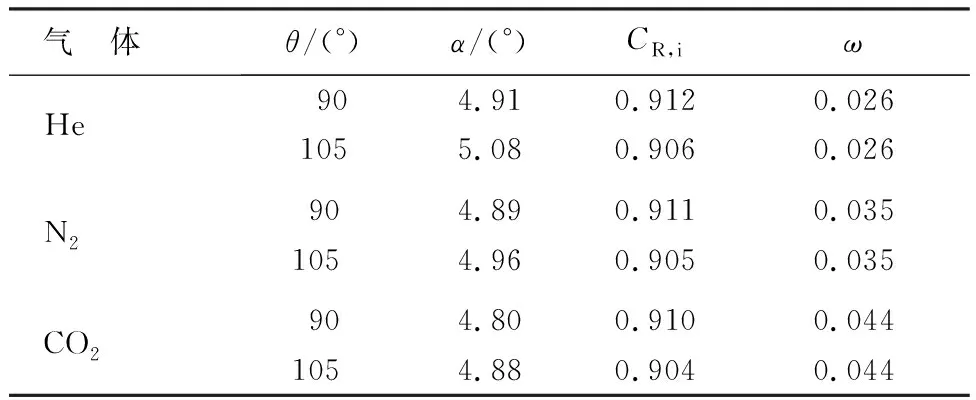
表2 不同注氣角度下矢量噴管性能參數對比Table 2 Comparison of vector nozzle performance parameter under different gas injection angles

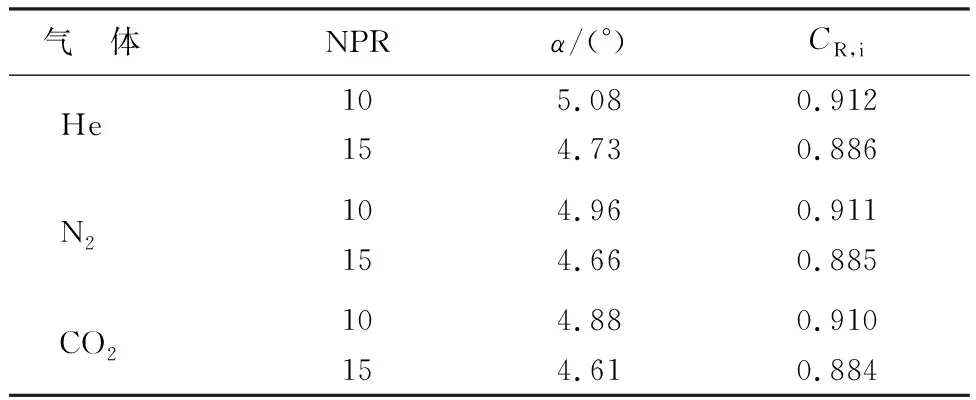
表3 不同NPR下矢量噴管性能參數對比Table 3 Comparison of vector nozzle performance parameter under different NPRs

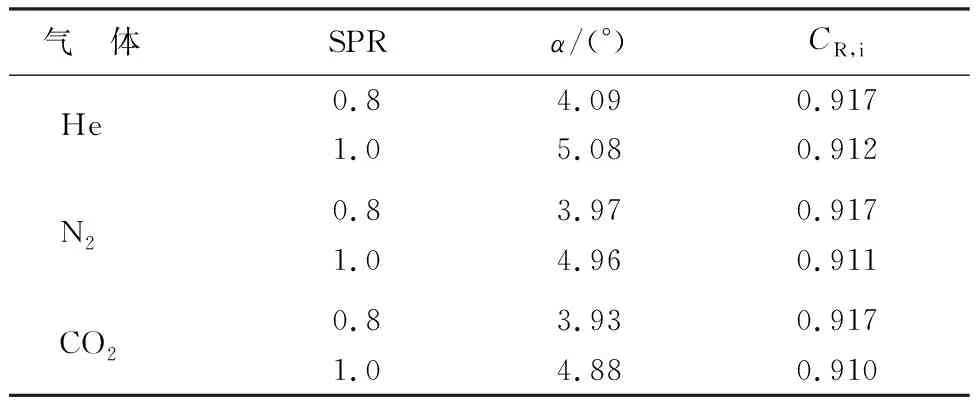
表4 不同SPR下矢量噴管性能參數對比Table 4 Comparison of vector nozzle performance parameter under different SPRs

4 結 論

本文通過在不同注氣角度、SPR和NPR條件下求解多組分Navier-Stokes方程，模擬了不同種類次流氣體噴注時，激波誘導推力矢量噴管的推力矢量性能。

1) 在相同的物性參數條件下，次流氣體的分子質量越小，次流與主流的質量流量比越小，所產生的矢量偏轉角越大，推力損失也越小。因此，質量分數小的次流氣體有著更高的推力矢量效率。

2) 在進行系統設計時，選用平均分子質量小的氣體作為次流氣源，或者將從燃燒室引出的高溫燃氣與分子質量小的氣體混合減小其平均分子質量，可以提高激波誘導推力矢量噴管的推力矢量性能。