MSCSG轉子不平衡振動原理分析與建模

夏長峰， 蔡遠文， 任元， 王衛杰， 樊亞洪， 尹增愿

(1. 航天工程大學研究生院, 北京 101416； 2. 航天工程大學宇航科學與技術系, 北京 101416； 3. 北京控制工程研究所, 北京 100190)

磁懸浮控制敏感陀螺(Magnetically Suspended Control and Sensing Gyroscope, MSCSG)是一種新概念陀螺[1-2]，其融合了磁懸浮控制力矩陀螺(Magnetically Suspended Control Momentum Gyroscope, MSCMG)對載體輸出控制力矩[3-4]以及轉子式速率陀螺儀對載體進行姿態測量[5-6]的功能，將航天器姿態控制系統的執行機構與敏感器合二為一，不僅繼承了MSCMG轉子系統無接觸、無摩擦、壽命長、精度高[7]的優點，還明顯降低了航天器姿態控制系統的體積、質量、功耗和成本。MSCSG轉子系統采用五自由度全主動控制，具有一定小角度的微框架效應，能夠瞬間輸出較大的陀螺力矩，實現姿態控制；載體姿態變化時，磁軸承對轉子沿徑向施加二自由度控制力矩，通過測量偏轉磁軸承的控制力矩間接實現姿態敏感。然而，受轉子質量分布不平衡因素的影響，磁軸承-轉子系統產生的擾動力矩傳遞到載體上，影響力矩輸出精度和姿態測量精度。因此，對MSCSG轉子系統進行不平衡振動控制是實現其測控一體化的必然要求，而對不平衡振動機理進行分析及動力學建模是實現不平衡振動控制的前提條件。

轉子不平衡是磁懸浮轉子系統產生振動的最主要因素[8]。目前，國內外學者對各類磁懸浮轉子不平衡振動的原理及建模研究取得了一系列成果。文獻[9-12]分析了質量分布不平衡條件下桿狀磁懸浮電機轉子的振動機理，并在此基礎上建立了磁軸承-轉子系統動力學模型；文獻[13-14]基于模態平衡理論分析了撓性轉速下桿狀磁懸浮電機轉子的運動特性，推導了柔性轉子不平衡振動模型；文獻[15-17]針對基于磁阻力磁軸承支承的MSCMG轉子系統存在不平衡擾動以及轉子檢測軸與旋轉軸不重合2種不同角度，分別建立轉子系統動力學模型；文獻[18-20]分析了基于混合磁軸承支承的MSCMG轉子系統不平衡振動機理，針對混合磁軸承對轉子扭轉自由度不存在主動可控電流的特殊性，在分析主被動通道磁力非線性的基礎上，建立了混合磁軸承支承的磁懸浮轉子動力學模型；文獻[21-22]在建立包含動不平衡的磁懸浮轉子系統動力學模型基礎上，分析了模型中不平衡量對轉子控制系統的影響。

由于MSCSG是一種新概念陀螺，采用雙球形轉子結構，通過具有線性特性的洛倫茲力磁軸承(Lorentz Force Magnetic Bearing，LFMB)支承，其支承原理與上述磁懸浮電機、MSCMG有較大區別，因此上述不平衡振動分析方法無法直接應用于MSCSG轉子系統。而對這類新型陀螺轉子的不平衡振動機理尚未開展系統的理論研究，關于其擾動量能觀性的解析性分析也未見報道。因此，本文在對MSCSG轉子系統工作機理進行分析的基礎上，對轉子不平衡問題進行了幾何描述，推導了高速轉子質量不平衡產生的擾動力矩數學模型，并在此基礎上對擾動量的可觀測性進行了解析性分析；建立了不平衡振動條件下磁軸承-轉子控制系統模型，分析了閉環控制系統不平衡振動的產生機理，并對不平衡振動的響應特性進行仿真，驗證了所建立模型的正確性；根據不平衡振動的特點提出了對其進行主動振動控制的要求。

1 MSCSG工作原理

MSCSG結構如圖1所示，主要由陀螺房、陀螺轉子、軸向磁軸承、力矩器、徑向磁軸承、旋轉電機、位移傳感器構成。其中，旋轉電機驅動轉子繞軸向高速旋轉，力矩器驅動轉子繞徑向偏轉，徑向磁軸承驅動轉子沿徑向平動，軸向磁軸承驅動轉子沿軸向平動。

圖1中，MSCSG的轉子組件為雙球形包絡面結構，由位于轉子軸向和徑向的2個共球心球缺組成，其中軸向球缺構成軸向磁軸承的轉子部分，徑向球缺構成徑向磁軸承的轉子部分。由于徑向磁軸承及軸向磁軸承的磁極都呈球狀，球面磁極產生的電磁力始終經過磁極球心，無論轉子在磁間隙內處于什么位置，都不會產生扭轉力矩，從而實現了平動自由度對徑向轉動自由度的解耦。因此，轉子徑向偏轉只受力矩器控制。

MSCSG采用LFMB為力矩器驅動轉子偏轉，LFMB產生的電磁力依據安培力定律，即磁感應強度為B的磁場中沿與磁場垂直方向放置長度為L的線圈，當流經線圈中電流為I時，線圈將受到大小為BIL的安培力作用。LFMB組件結構如圖2所示。轉子外沿一周的狹長內壁上放置著上、下2層磁鋼，2層磁鋼的內、外磁鋼間充磁方向相反，因此形成了如圖2中虛線所示的閉合磁場。LFMB的定子部分由4組匝數相同的線圈構成，位于內、外磁鋼間的狹縫中，沿LFMB周向均勻分布，4組線圈成對使用，正對的2組線圈為一對，用于實現轉子的二自由度偏轉控制。

以LFMB幾何中心O為原點定義定子坐標系O-XYZ，其中X軸與Y軸分別與相對方向2組線圈中心線重合，Z軸方向根據右手定則確定。當與磁場垂直方向放置的線圈通入電流時，線圈的上下兩部分將分別產生垂直于線圈及磁場方向的安培力，合力大小為

圖1 MSCSG結構示意圖Fig.1 Structure diagram of MSCSG

F=2nBIL

(1)

式中：n為線圈匝數。

根據如圖2所示的LFMB工作原理圖，LFMB提供的X、Y方向偏轉力矩分別為

(2)

式中：iX+、iX-分別為X軸正、負方向上的線圈驅動電流；iY+、iY-分別為Y軸正、負方向上線圈驅動電流；lm為LFMB定子半徑。令iY+=iα，iX-=iβ，當相對方向線圈通入大小相等、方向相同的電流時，線圈將產生大小相等、方向相反的安培力，形成力偶驅動轉子徑向偏轉，此時，根據式(2)可知偏轉力矩pX、pY表達式分別為

(3)

圖2 LFMB工作原理Fig.2 Working principle of LFMB

2 MSCSG轉子不平衡問題幾何分析

MSCSG轉子除軸向旋轉自由度由電機驅動控制，其余5個由磁軸承懸浮的自由度均需通過傳感器來獲得轉子位置信息。該位置信息既提供給閉環控制器進行反饋控制，也作為轉子懸浮工作狀態的判定依據。轉子偏轉自由度為LFMB控制的自由度，需要位移傳感器測量轉子的位置信息來實現偏轉通道的偏轉角信息反饋。MSCSG偏轉通道4個位移傳感器安裝在上陀螺房的傳感器支架上，配置方式如圖3(a)所示，4個傳感器在同一平面上，過定子坐標系原點O對檢測面投影，如圖3(b)中黑色虛線所示。

以定子坐標系原點O為原點定義幾何坐標系O-xyz，其中x軸與y軸分別與相對方向2組線圈中心線重合，z軸方向根據右手定則確定。由于線圈對向中心線與幾何坐標系的x軸、y軸重合，因此定子坐標系與幾何坐標系重合。hy+、hy-、hx+、hx-分別為投影在y軸正、負方向以及x軸正、負方向上的軸向傳感器測得的轉子軸向位移。轉子偏轉角可以通過同一條直線上2個傳感器位置差獲得。以轉子繞x軸偏轉的α通道為例，如圖4所示，轉子的偏轉角可以通過轉子在該通道兩端的位置差與對應傳感器間跨距比值獲取。計算公式為

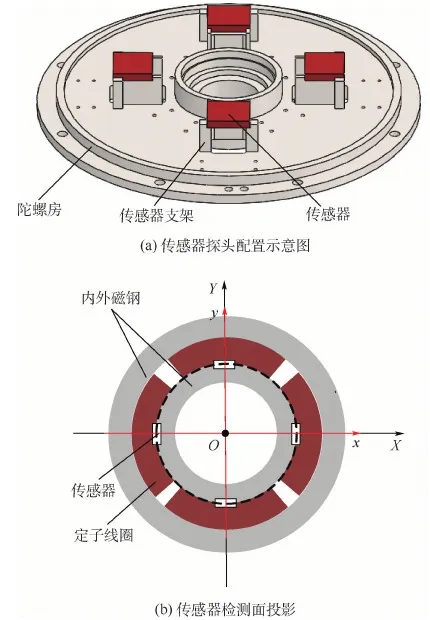
圖3 傳感器探頭配置及檢測面示意圖Fig.3 Schematic diagram of sensor probe configuration and detection surface

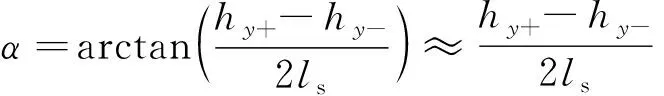
(4)

同理，轉子繞y軸偏轉的β通道偏轉角計算公式為

(5)

定義轉子慣性軸為高速轉子旋轉自由度所對應的慣性主軸。轉子質量分布均勻的情況下，慣性軸與幾何軸相一致。然而，轉子材料不均勻和加工、裝配等誤差會使轉子質量分布不平衡，導致轉子的慣性軸與幾何軸不再一致，從而使轉子慣性軸相對于幾何軸產生如圖5(a)所示的偏轉。質量分布不平衡條件下，MSCSG轉子慣性軸與幾何軸的角位置關系如圖5(b)所示，(αg,βg)為幾何軸的角坐標，(αi,βi)為慣性軸的角坐標，g(ξ,ζ)為與轉子固連的旋轉角坐標系，轉子慣性主軸在g(ξ,ζ)中的幅值和相位分別為δ和φ。

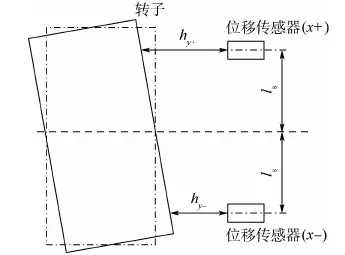
圖4 偏轉角檢測原理Fig.4 Testing principle of deflection angle

圖5 轉子慣性軸與幾何軸位置關系Fig.5 Position relation between inertial axis and geometric axis of rotor

由圖5中的轉子慣性軸與幾何軸間關系可知，慣性坐標系下轉子偏轉角信息αi、βi表達式為

(6)

式中，α、β分別由式(4)和式(5)得到；Ω為轉子軸向轉速；Δα、Δβ分別為徑向兩偏轉角在慣性坐標系與幾何坐標系下的偏差。

3 磁軸承-轉子控制系統不平衡振動建模

3.1 不平衡擾動項能觀性分析

根據歐拉定理寫出陀螺技術方程[23]：

(7)

式中：Jx、Jy分別為轉子在x、y方向的轉動慣量，且Jx、Jy數值上與轉子徑向轉動慣量Jr相等；Jz為轉子在z方向的轉動慣量。

由于控制系統中各測量值都是在幾何坐標系中獲取，而陀螺技術方程是在慣性坐標系下定義。因此，將式(6)中轉子慣性坐標系與幾何坐標系間的關系表達式代入式(7)，得到慣性坐標系下轉子信息表達式為

(8)

根據式(8)可知，不平衡擾動力矩表達式分別為

(9)

式中：

(10)

根據以上分析可知，當轉子質量分布不均勻時，轉子的幾何軸與慣性軸不再一致，此時轉子系統將產生不平衡擾動力矩，作用于與定子固連的基座，引起載體航天器的振動。

將式(3)、式(9)代入式(8)，得

(11)

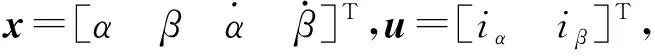
(12)

式中：

(13)

(14)

d=[pdx/(4nBLlm)pdy/(4nBLlm)]T

(15)

對擾動項d列寫狀態方程，取狀態變量T=[TxTy]T，則擾動項pd=[pdxpdy]T可用如下模型表述：

(16)

對于式(16)表述的擾動模型，其能觀性矩陣N表達式為

N=[VVW]T

(17)

從式(17)表達式可知，轉速Ω不等于0時，能觀性矩陣的秩rank(N)=2，式(16)能觀，因此系統的不平衡擾動可測。

3.2 含振動源的磁軸承-轉子控制系統動力學建模

轉子不平衡條件下，MSCSG轉子偏轉控制系統閉環結構如圖6所示。控制通道主要包括傳感器、抗混疊濾波器、控制器和功率放大器構成。閉合回路中，傳感器檢測到轉子偏轉信息并通過抗混疊濾波器進行降噪處理，控制器根據偏轉信息確定偏轉指令，隨后功率放大器將偏轉指令轉化為控制電流，驅動LFMB產生控制力矩，使轉子偏轉至指定參考位置。

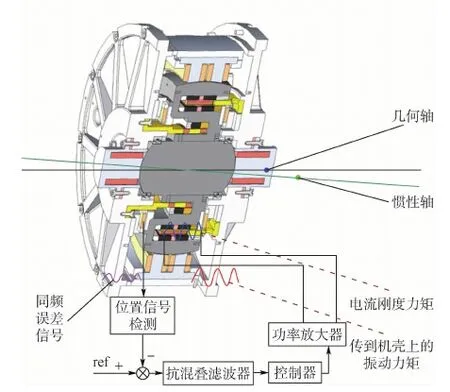
圖6 轉子不平衡條件下MSCSG轉子偏轉控制 系統閉環結構Fig.6 Closed-loop structure of rotor tilt control system in MSCSG considering rotor imbalance

由式(7)可知，轉子偏轉通道間存在耦合，因此為抑制陀螺耦合效應，控制器采用基于交叉濾波的PID控制算法，其中的PID控制器和交叉濾波器傳遞函數表達式分別為

(18)

(19)

式中：kp、ki、kd分別為比例、積分、微分系數；ωD為不完全微分系數；kl和kh分別為低通和高通濾波器增益；a1l、a2l為低通濾波器系數；a1h、a2h為高通濾波器系數。

由如圖4所示的控制系統框圖可知，根據轉子偏轉角可確定控制電流為

(20)

將式(3)、式(6)、式(20)代入式(7)，得到MSCSG轉子偏轉動力學方程組：

(21)

將式(21)進行拉普拉斯變換得

(22)

對式(22)進行化簡，得到

(23)

式(23)的等效閉環控制系統框圖如圖7所示，αr、βr為偏轉指令信號。對圖7中的轉子不平衡條件下MSCSG轉子系統模型進行分析可知，轉子不平衡量經過磁軸承控制器和功率放大器進入閉環控制系統，通過LFMB產生電流剛度力矩，引起轉子產生不平衡振動。

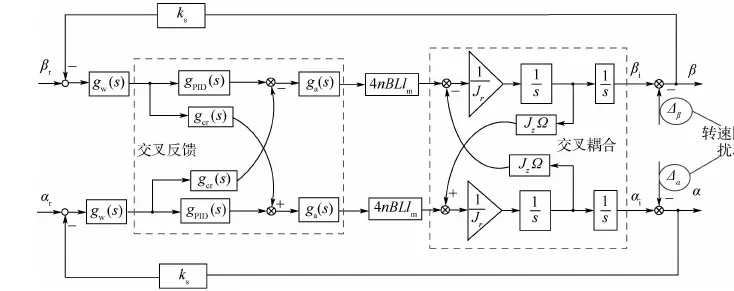
圖7 磁軸承-轉子控制系統框圖Fig.7 Block diagram of magnetic bearing-rotor control system

4 仿真分析

根據本文所建立的MSCSG磁軸承-轉子控制系統不平衡振動模型，對慣性軸與幾何軸不一致條件下磁軸承-轉子控制系統產生的不平衡振動力矩進行仿真分析。仿真參數如表1所示，其中，轉子參數根據MSCSG設計指標確定，控制器相關參數依照文獻[23]設定。表1中：ka為功率放大器增益；ωa為功率放大器截止頻率；ωf為抗混疊濾波器截止頻率。

轉子轉速由0升至6 000 r/min時，不平衡振動力矩的響應仿真結果如圖8所示。可知，瀑布圖中包含了明顯的轉速同頻成分，不平衡振動頻率隨轉子轉速升高而增加，不平衡振動幅值與轉子轉速呈遞增的趨勢。因此，不平衡振動仿真結果與動力學模型所描述不平衡因素的頻率特性相一致，驗證了本文所建立模型的正確性。根據以上分析可知，要想實現MSCSG轉子系統的主動振動控制，必須對轉子不平衡引起的轉速同頻擾動量進行抑制。

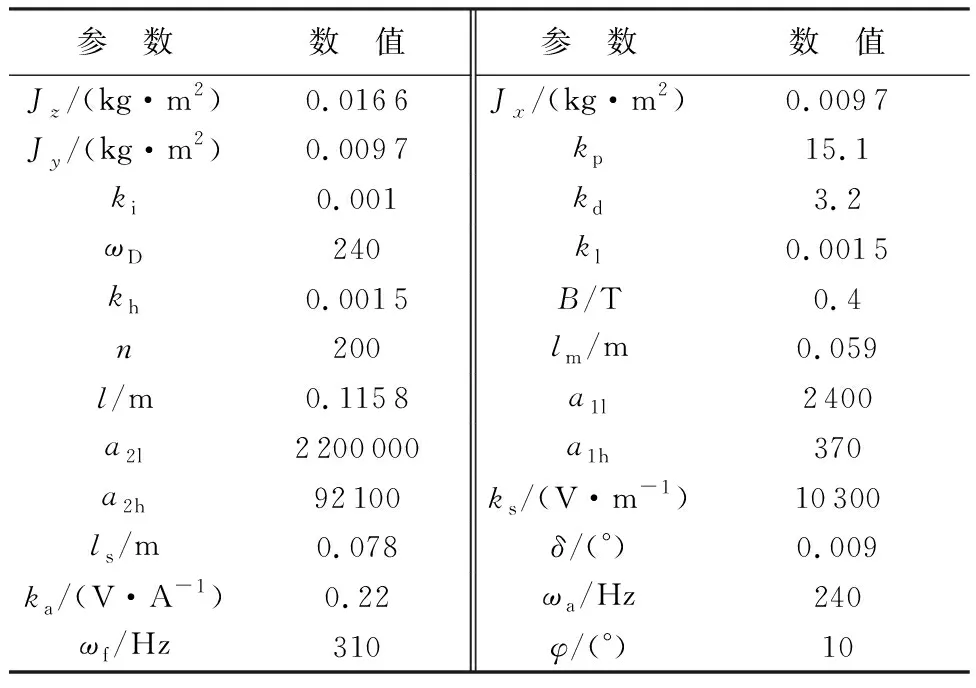
表1 MSCSG系統參數Table 1 Parameters of MSCSG system

圖8 不平衡振動響應仿真結果Fig.8 Simulation results of unbalance vibration response

5 結 論

1) MSCSG轉子質量分布不平衡條件下，轉子慣性主軸與幾何主軸不一致，導致轉子系統產生不平衡振動力矩。

2) MSCSG轉子轉速不為零的條件下，轉子質量分布不平衡產生的振動力矩可觀測。

3) MSCSG轉子不平衡量經過磁軸承-轉子控制系統產生電流剛度力矩，引起的振動與轉子轉速同頻，為實現對轉子的主動振動控制，必須對轉速同頻擾動量進行抑制。