無窮區間上分數階微分方程m-點邊值問題的正解

王威璇, 翟成波

(山西大學 數學科學學院, 太原 030006)

0 引 言

分數階微分方程在物理學、 力學、 控制理論和經濟管理等領域應用廣泛[1-17], 其中無窮區間上的分數階微分方程也得到廣泛關注[2-6,8-9,17]. 但無窮區間上非線性分數階微分方程邊值問題的研究目前處于初始階段, 特別是對于無窮區間上分數階邊值問題正解的研究文獻報道較少. 文獻[4]研究了如下分數階微分方程m-點邊值問題:

(1)

正解的存在性, 利用Leggett-Williams不動點定理, 得到了其3個正解的存在性, 但未考慮正解的唯一性. 受文獻[4,18-19]啟發, 本文利用算子之和的不動點定理, 考慮如下一類無窮區間上非線性分數階微分方程m-點邊值問題正解的存在性與唯一性:

(2)

1 預備知識

定義1[7]函數f:+→+的s階Riemann-Liouville分數階積分定義為

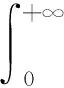
定義2[7]函數f:+→+的s階Riemann-Liouville分數階導數定義為

其中:s>0;n為大于或等于s的最小整數.

引理1[4]設f∈C[0,+∞), 則分數階邊值問題:

引理2[4]Green函數G1(t,s)滿足如下性質:

1) 當(t,s)∈[0,+∞)×[0,+∞)時,G1(t,s)是連續的, 且G1(t,s)≥0;

2)G1(t,s)關于t是嚴格增的;

3) 當0

設E是實Banach空間,θ是E中的零元.P?E是一個錐, “≤”是由P引出的半序, 即v-u∈P?u≤v. 如果存在常數N>0, 使得u,v∈E,θ≤u≤v?‖u‖≤N‖v‖, 則錐P稱為正規的, 最小的N稱為P的正規常數.

定義3[20]如果u≤v, 有Tu≤Tv(Tu≥Tv), 則稱T:E→E是增算子(減算子).

定義4[20]設0<γ<1, 如果對τ∈(0,1),u∈P, 有T(τu)≥τγTu, 則稱算子T:P→P是γ-凹的. 如果對τ>0,u∈P, 有T(τu)≥τTu, 則稱算子T:P→P是次齊次的.

對任意的u,v∈E,u～v表示存在λ>0和μ>0, 使得λu≤v≤μu. 顯然, ～是等價關系. 給定h>θ(i.e.,h≥θ且h≠θ), 定義集合Ph={u∈E|u～h}, 易得Ph?P.

引理3[18]設P是E中的正規錐,A:P→P是增的γ-凹算子,B:P→P是增的次齊次算子. 若下列條件成立:

1) 存在h>θ, 使得Ah∈Ph,Bh∈Ph;

2) 存在常數δ0>0, 使得Au>δ0Bu,u∈P.

則算子方程

Au+Bu=u

(5)

在Ph中有唯一解u*, 且對于給定的v0∈Ph, 做迭代序列vn=Avn-1+Bvn-1(n=1,2,…), 則{vn}收斂于u*.

引理4[19]設P是E中的正規錐,A:P→P是增算子,B:P→P是減算子. 若下列條件成立:

1) 對t∈(0,1), 存在φi(t)∈(t,1)(i=1,2), 使得

(6)

2) 存在h0∈Ph, 使得Ah0+Bh0∈Ph.

則算子方程(5)在Ph中有唯一解u*, 且對給定的u0,v0∈Ph, 做迭代序列

un=Aun-1+Bvn-1,vn=Avn-1+Bun-1,n=1,2,…

則{un},{vn}收斂于u*.

注2當B是一個零算子時, 引理3和引理4仍成立.

2 主要結果

假設:

(H1)f(t,u),g(t,u): [0,+∞)×[0,+∞)→[0,+∞)連續且關于第二個變量是增的;

(H2) 當u有界時,f(t,(1+tα-1)u),g(t,(1+tα-1)u)關于t∈[0,+∞)有界;

(H3) 存在常數γ∈(0,1), 使得f(t,τu)≥τγf(t,u),t∈[0,+∞),τ∈(0,1),u∈[0,+∞), 對任意的t∈[0,+∞),τ∈(0,1),u∈[0,+∞), 有g(t,τu)≥τg(t,u);

定理1若假設條件(H1)～(H4)成立, 則邊值問題(2)在Ph中有唯一正解u*, 這里h(t)=tα-1,t∈[0,+∞), 且對于Ph中任意的u0, 做迭代

有{un+1}收斂到u*(t), 其中G(t,s)由式(3)給出.

證明: 由引理1知, 邊值問題(2)可轉化為積分方程

其中G(t,s)由式(3)給出. 定義E上兩個算子A,B如下:

再由引理2易得Au∈C[0,+∞), 所以A:P→P. 同理有B:P→P.

當u,v∈P且u≥v時, 有u(t)≥v(t),t∈[0,+∞). 由假設條件(H1)得

即Au≥Av, 從而A是一個增算子. 同理, 由假設條件(H1)知,B是增算子. 對τ(0,1)和u∈P, 由假設條件(H3)知,

因此A是一個γ-凹算子,B是一個次齊次算子.

下證引理3的條件2)成立. 一方面, 由假設條件(H2)可得

另一方面, 有

因此l1h(t)≤Ah(t)≤l2h(t),t∈[0,+∞), 即l1h≤Ah≤l2h, 所以Ah∈Ph. 同理可證Bh∈Ph.

對u∈P, 由假設條件(H4)知,

即Au≥δBu,u∈P. 因此A,B滿足引理3的所有條件. 從而算子方程Au+Bu=u在Ph中有唯一解u*; 且對于初值u0∈Ph, 構造迭代序列un=Aun-1+Bun-1(n=1,2,…), 當n→∞時, 有un→u*, 即邊值問題(2)有唯一解u*∈Ph, 序列

收斂到u*(t). 證畢.

假設:

(H5) 當u有界時,f(t,(1+tα-1)u)關于t在[0,+∞)內有界;

(H7) 存在常數γ∈(0,1), 使得f(t,τx)≥τγf(t,x),t∈[0,+∞),τ∈(0,1),x∈[0,+∞).

由注2和定理1可得：

推論1假設α,ξi,βi(i=1,2,…,m-2)滿足邊值問題(2)的條件, 且假設條件(H5)～(H6)成立, 則下列邊值問題：

(7)

在Ph中有唯一解u*, 其中h(t)=tα-1,t∈[0,+∞). 對初值u0∈Ph, 序列

收斂到u*(t), 其中G(t,s)由式(3)給出.

假設:

(H8)f(t,u),g(t,u): [0,+∞)×[0,+∞)→[0,+∞)連續, 且f(t,u)關于u是增的,g(t,u)關于u是減的;

(H9) 對于τ∈(0,1), 存在φi(τ)∈(τ,1)(i=1,2), 使得

定理2假設條件(H2),(H8),(H9)成立, 且f(t,0)和g(t,0)均不恒為零, 則邊值問題(2)在Ph中有唯一正解u*, 這里h(t)=tα-1,t∈[0,+∞). 對于初值u0,v0∈Ph, 序列

收斂到u*(t), 這里G(t,s)由式(3)給出.

證明: 算子A:P→E和B:P→E分別定義為

下證引理4的條件2)成立. 一方面, 由假設條件(H2)知,

另一方面, 有

由假設條件(H8)和定理1的證明知,l4≥l3>0, 于是l4h(t)≥Ah(t)+Bh(t)≥l3h(t),t∈[0,+∞), 因此Ah+Bh∈Ph， 所以引理4的所有條件都滿足. 算子方程Au+Bu=u在Ph中有唯一解u*， 且對于初值u0,v0∈Ph, 序列

un=Aun-1+Bvn-1,vn=Avn-1+Bun-1,n=1,2,…

收斂到u*, 即邊值問題(2)在Ph中有唯一正解u*. 對任意初值u0,v0∈Ph, 做序列

當n→∞時, 有un(t)→u*(t),vn(t)→u*(t). 證畢.

假設:

(H10) 對于τ∈(0,1), 存在φ(τ)∈(τ,1), 使得f(t,τu)≥φ(τ)f(t,u),t∈[0,+∞),u∈[0,+∞).

由注2和定理3可得：

推論2假設α,ξi,βi(i=1,2,…,m-2)滿足邊值問題(2)的條件, 且假設條件(H5),(H6),(H10)成立, 則邊值問題(7)有唯一解u*∈Ph, 其中h(t)=tα-1,t∈[0,+∞). 對初值u0∈Ph, 序列

收斂到u*(t), 其中G(t,s)由式(3)給出.

3 應用實例

例1考察無窮區間上分數階微分方程:

(8)

顯然,f(t,u),g(t,u): [0,+∞)×[0,+∞)→[0,+∞)均連續, 且關于u是增的, 滿足假設條件(H1). 當0≤u≤M時, 有

其中t∈[0,+∞). 滿足假設條件(H2), 且f(t,0)>0,g(t,0)>0.令γ=1/2, 對t∈[0,+∞),τ∈(0,1),u∈[0,+∞), 有

滿足假設條件(H2). 此外, 顯然a(t),b(t)關于t是連續的, 且

取δ∈(0,1], 則

因此定理1的所有條件都滿足. 所以邊值問題(8)有唯一正解u*∈Ph,h(t)=t3/2,t∈[0,+∞). 對初值u0∈Ph, 做序列

則有un(t)→u*(t),n→∞.

例2考察無窮區間上分數階微分方程:

(9)

滿足假設條件(H9), 且f(t,0)>0,g(t,0)>0. 從而滿足假設條件(H8). 設φ1(τ)=τα1,φ2(τ)=τα2,τ∈(0,1), 則φ1(τ),φ2(τ)∈(τ,1). 于是, 對t∈[0,+∞),τ∈(0,1),u∈[0,+∞), 有

因此定理2的所有條件都滿足. 所以邊值問題(9)有唯一正解u*∈Ph, 其中h(t)=tα-1,t∈[0,+∞). 對初值u0,v0∈Ph, 做序列

則有un(t)→u*(t),vn(t)→u*(t),n→∞.