參數與時滯相關延遲振子的穩(wěn)定性及Hopf分岔分析
羅佳偉, 徐 旭
(1. 遼寧大學 數學院, 沈陽 110036; 2. 吉林大學 數學學院, 長春 130012)
0 引 言
涉及反饋控制的系統(tǒng)幾乎都含有時滯, 即需要一段時間來感應信息, 然后做出反應. 由于控制信號不能及時到達, 熱量和能量在信號傳遞過程中可能會減弱, 從而導致控制信號的強度或能量的衰減, 特別是長時間延遲的遠程控制[1]. 這種情形下可考慮為參數與時滯相關的時滯系統(tǒng)建模. 文獻[2]研究了一個參數與時滯相關的單神經元模型:
(1)
其中:k>0;a>0;τ≥0是時滯;b(τ)>0稱為記憶函數, 由于神經元的記憶效應通常隨時間遠離當前時刻而減弱, 因此記憶函數b(τ)>0是時滯τ的單調遞減函數. 模型(1)由以下時滯神經元模型當核函數取Dirac函數時得到:
(2)
當非線性函數取簡單的雙曲正切函數f(t)=tanh(t)時, 方程(1)有混沌吸引子. 如果在方程(1)中引入慣性項, 則有
(3)
其中β是阻尼系數. 系統(tǒng)(3)是由一個神經元模型加上慣性項得到的, 目前, 關于慣性神經元振動控制系統(tǒng)的研究已被廣泛關注[3-6]. 這里, 非線性函數f(·)可視為振動控制系統(tǒng)的反饋函數, 記憶函數b(τ)可視為控制信號強度或能量的衰減. 本文分析振子系統(tǒng)(3)的動力學, 并研究記憶函數對振動控制系統(tǒng)穩(wěn)定性的影響.
1 線性穩(wěn)定性分析
令y(t)=x(t)-b(τ)x(t-τ), 則方程(3)可寫成
(4)
令dy(t)/dt=z(t), 則方程(4)可以寫成:
(5)
假設激活函數滿足以下條件:
f(0)=0,f′(0)>0,f∈C1(R).
(6)
易見方程(5)在條件(6)下有零平衡點. 方程(5)在零平衡點處的線性化方程為
(7)
其中:A=af′(0);B(τ)=ab(τ)f′(0). 由于f′(0)>0, 因此A>0,B(τ)>0. 將u1(t)=C1eλt和u2(t)=C2eλt代入式(7)得
(8)
如果方程(8)有非平凡解, 則
(9)
即
D(λ)=λ2+βλ+k-A+B(τ)e-λτ=0.
(10)
如果系統(tǒng)所有特征根都具有負的實部, 則方程(4)的平衡點是漸近穩(wěn)定的. 因此, 穩(wěn)定性邊界由λ=0和λ=±iω(ω>0)決定. 由于λ=0的情形較簡單, 因此本文只考慮λ=iω的情形. 將λ=iω代入方程(10)得
(11)
令k-A=p, 由方程(11)可得
F(ω)=(ω2-p)2+ω2β2-B2(τ)=0,
(12)
ω4+(β2-2p)ω2+p2-B2(τ)=0.
(13)
進一步, 由方程(13)可得
(14)
其中Δ=(2p-β2)2-4[p2-B(τ)2].
下面討論方程(13)根的情形:
情形1) 如果Δ=(2p-β2)2-4(p2-B2)<0, 則方程(13)沒有實根, 方程(4)即為參數與時滯無關的, 此時對于任意時滯, 系統(tǒng)的穩(wěn)定性都依賴于系統(tǒng)沒有時滯的情形.
情形2) 如果2p-β2>0,Δ=0, 則由方程(14)得ω+=ω-, 方程(10)有重共軛虛根, 此時系統(tǒng)為退化的情形, 特征根通過虛軸的方向很難確定. 因此, 為簡單, 可假設特征方程(10)只有單根的情形.
情形3) 如果2p-β2>0,Δ>0,p2-B2>0, 則方程(10)有根λ=±iω+和λ=±iω-(ω+>ω->0).
情形4) 如果p2-B2<0,Δ>0, 則方程(10)有根λ=±iω+,ω+>0.
對于情形3)和情形4), 需要確定特征根實部隨τ的變化情況. 注意到方程(10)的根是時滯τ的函數, 由方程(11)可得
(15)
假設方程(15)有一系列正的單根τ0,τ1,…, 則在τ0,τ1,…處存在單共軛虛根λ=±iω(τ), 穩(wěn)定性切換發(fā)生在下列函數的零點處:
Sj(τ)=τ-τj(τ),j∈N0.
(16)
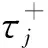
(17)
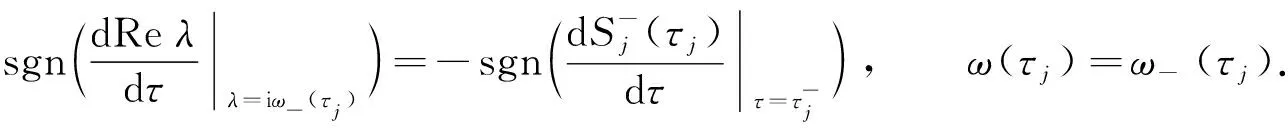
(18)
文獻[7]給出了參數與時滯相關的時滯微分方程穩(wěn)定切換的證明, 因此下面給出定理1的一個簡單證明.
證明: 對方程(10)關于時滯τ求導得
(19)
則
(20)
(21)
當λ=iω時, 可得
(22)
簡單計算得
(23)
對方程(12)關于τ求導得
(24)
將式(24)代入式(23)得
(25)
由方程(15)可得τj(τ)的表達式為
(m=2j或m=2j+1),
(26)
且
(27)
比較方程(25)與方程(27)便可得所證結論. 證畢.
事實上, 可以用MAPLE等數學軟件定位函數Sj(τ)=τ-τj(τ)(j∈N0)的零點來確定穩(wěn)定性切換的臨界時滯, 而特征根通過虛軸的方向可以由函數Sj(τ)圖像的斜率確定. 當系統(tǒng)的記憶函數取為指數衰減函數b(τ)=b0e-ατ(b0>0,α>0), 激活函數為f(·)=tanh(·)時, 有
如果ω2(τ)>p, 則m=2j; 如果ω2(τ) 圖1 當α=0.1時關于τ的函數圖像Fig.1 Functional images of on τ when α=0.1 圖2 當α=0.1時, 對于不同的時滯τ系統(tǒng)(3)的穩(wěn)定性切換曲線Fig.2 Curves of stability switches of system (3) for different delays τ when α=0.1 圖3為參數α, 即記憶函數b(τ)對系統(tǒng)穩(wěn)定性的影響. 由上述結果可見, 隨著τ的增加, 系統(tǒng)發(fā)生有限次穩(wěn)定性切換, 系統(tǒng)的零平衡點最終是穩(wěn)定的. 圖3 參數α對系統(tǒng)穩(wěn)定性的影響Fig.3 Effects of parameter α on stability of system 由上述分析可見, 當τ=Γ0∈{τ0,τ1,τ2,…τN}(N為正整數)時, 特征方程有一對純虛根. 因此, 希望方程(4)在Γ0處發(fā)生Hopf分岔. 考慮方程(10)的一對純虛根λc=±iωc(τ)(ω>0), 為了證明λc=iωc(τ)是單根, 需要指出D′(λc)≠0, 這里 D′(λc)=2iωc+β-τB(τ)e-iωcτ. (28) 假設D′(λc)=0, 分離實部和虛部得 (29) 由于ωc>0必需滿足方程(11), 因此, 由方程(11)可得 (30) 由式(29),(30)可得 (31) 式(31)等價于方程(14)中Δ=0. 因此, 排除滿足方程(31)中ωc的值,λc=iωc(τ)是方程(10)的單根, 表明系統(tǒng)(4)滿足Hopf分岔的條件, 并且在τ=Γ0處發(fā)生Hopf分岔. 下面根據規(guī)范型和中心流形定理[8]研究系統(tǒng)(4)Hopf分岔的方向及分岔周期解的穩(wěn)定性和周期. 為簡便, 令τ=Γ0+μ,μ∈, 則μ=0是系統(tǒng)(4)的Hopf分岔點. 假設函數f滿足下列條件:f∈C3(),uf(u)≠0,u≠0. 將方程(5)在平衡點展開到一階、 二階、 三階, 得 (32) 定義Banach空間上的實值連續(xù)函數C=C([-Γ0,0],). 令φ∈C, 以最大范數定義線性算子 Lμφ=Mφ(0)+Bφ(-τ), (33) 及一個非線性算子 (34) 其中: 由Riesz表示定理知, 存在一個矩陣, 其元素是有界變量函數η(θ,μ),θ∈[-Γ0, 0], 使得 (35) 事實上, 如果dη(θ,μ)選擇為dη(θ,μ)=Mδ(θ)+Bδ(θ+τ), 則式(35)滿足. 對φ∈C1([-Γ0,0],2), 定義 (36) (37) 則式(32)可寫成如下向量的形式: (38) 這里u=(u1,u2)T,ut=u(t+θ),θ∈[-Γ0,0]. 對ψ∈C1([0,Γ0],(2)*),A的伴隨算子A*定義為 (39) 和一個雙線性內積 (40) 其中η(θ)=η(θ,0). 可以證明A*是A對于該雙線性形式的伴隨算子. 為了確定算子A的Poincaré標準型, 需要計算算子A的屬于特征根iω0的特征向量h及算子A*的屬于特征根-iω0的特征向量h*. 令 (41) (42) 為了確定〈h*,h〉=1, 需要確定D值. 事實上, 由方程(40)可知 (43) 利用文獻[8]的方法, 計算描述μ=0處中心流形Ω0的坐標. 令ut=u(t+θ)(θ∈[-Γ0,0))為方程(32)在μ=0處的解. 定義 z(t)=〈h*,ut〉,W(t,θ)=ut(θ)-2Re[z(t)h(θ)]. (45) (46) (47) 其中 (48) 方程(47)可以寫成 (49) 其中 (50) 從而由方程(45),(48)得 這里 (52) 注意到 (53) 因此 于是 (55) 比較系數可得 (56) 由文獻[8], 分岔周期解的關鍵性質由下列參數決定: (57) 定理2假設定理1中的條件滿足, 則系統(tǒng)(4)在τ=Γ0處發(fā)生Hopf分岔. 式(57)中的參數μ2決定Hopf分岔的方向: 如果μ2>0(<0), 則Hopf分岔是超臨界的(亞臨界的);β2決定由平衡點處分岔周期解的穩(wěn)定性: 如果β2<0(>0), 則分岔周期解是穩(wěn)定的(不穩(wěn)定的);T(2)決定周期解的周期: 如果T(2)>0(<0), 則周期增大(減小). 則系統(tǒng)(4)Hopf分岔的方向和周期解的穩(wěn)定性由式(57)中的參數μ2和β2決定. 證畢. 綜上所述, 本文通過分析一個參數與時滯相關的振子的穩(wěn)定性切換及Hopf分岔, 根據規(guī)范型理論和中心流形定理, 得到了系統(tǒng)的分岔方向與分岔周期解的穩(wěn)定性. 結果表明, 當時滯從0增大到+∞時, 參數與時滯相關的振子將發(fā)生有限次穩(wěn)定性切換, 但系統(tǒng)最終可能是穩(wěn)定、 不穩(wěn)定, 或者在穩(wěn)定與不穩(wěn)定之間切換, 適當大小的時滯可以穩(wěn)定系統(tǒng). 此外, 記憶函數b(τ)可視為影響系統(tǒng)的因素, 因此可用來控制系統(tǒng)的動力學性質.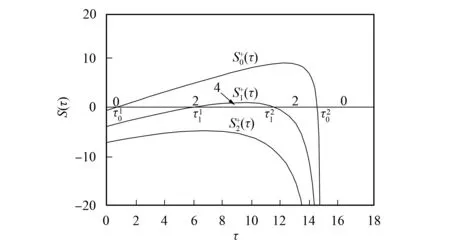
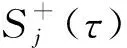


2 Hopf分岔分析