聯系一些特殊函數的Hilbert型積分不等式及其算子范數表達式
劉 瓊
(邵陽學院 理學院, 湖南 邵陽 422000)
0 引 言

(1)
這里常數因子π是最佳值. 不等式(1)在分析學及偏微分方程理論中應用廣泛[1-2]. 目前, 關于Hilbert型積分不等式及其推廣的研究已取得許多成果[3-13]. 楊必成[14]給出了一個新的具有指數函數核的Hilbert型積分不等式:
(2)
1 預備知識
下面參考文獻[15], 給出一些特殊函數的定義.
1) 設復數s的實部Re(s)>0, Gamma函數Γ(s)和不完全Gamma函數Γ(s,α)分別定義為

(3)

(4)
2) 設u,v>0, Beta函數B(u,v)定義為
(5)
3) 設α,β,z>0, 合流超幾何函數(又稱Kummer函數)1F1(α,β,z)定義為
(6)
這里
由式(6), 當0<λ<4-μ時, 有
(7)
4) Whittaker函數M(k,m,z)定義為
(8)
由式(7),(8), 有
(9)
設0<λ<2-μ, 由式(5),(9), 可得
設0<λ<2-3μ, 令λt=u, 由式(4), 可得
(11)

則
ω(λ,μ,x)=ω(λ,μ,y)=C(λ,μ),
其中
(12)
證明: 令xy=t, 由式(10),(11), 可得
類似可得ω(λ,μ,y)=C(λ,μ).

則有
證明: 易得

2 主要結果及應用


則有
這里常數因子C(λ,μ)(同式(12))是最佳值.
證明: 由帶權H?lder不等式[17]和引理1, 有
如果式(16)中等號成立, 則存在不全為零的常數A和B, 使得
在(0,∞)×(0,∞)內幾乎處處成立, 于是存在常數C≠0, 使得
Axp(λ+μ)/2fp(x)=Byq(λ+μ)/2gq(y)=C

C(λ,μ)(1-o(1)) 令ε→0+, 得K≥C(λ,μ), 與K 定理2在與定理1相同的條件下, 有 (17) 這里常數因子Cp(λ,μ)是最佳值, 且不等式(17)和不等式(15)等價. 設 則當n≥n0時, 由式(15), 可得 由式(18)有 令n→∞, 即有 表明應用式(15),(18),(19)取嚴格不等式號的條件均滿足, 因此不等式(17)成立. 另一方面, 設式(17)成立, 由H?lder’s不等式, 有 圖1 λ,μ的取值范圍Fig.1 Value range of λ and μ 即式(15)成立, 所以式(17)與式(15)等價. 如果式(17)的常數因子不是最佳值, 則由式(17)可知, 式(15)的常數因子也不是最佳值, 與定理1的結論矛盾, 所以式(17)的常數因子Cp(λ,μ)是最佳值. 證畢. 下面給出簡單應用. 在式(15),(17)中選取一些合適的參數, 借助MAPLE數學軟件計算C(λ,μ)的值, 可得文獻中的一些結果及一些新的有意義的不等式. 參數值λ,μ的取值范圍如圖1所示. (20) 這里常數因子π是最佳值. (22) 例3取λ=1,μ=-1,p=q=2, 計算式(12), 有 C(1,-1)=1+e-1. ψ1-p(y)=y(p/q)[1-q(λ+μ)/2]. 定義如下賦范線性空間: 由式(17), 有 (25) 根據式(25), 算子T是有界的, 即 又因為常數因子C(λ,μ)是最佳值, 故‖T‖=C(λ,μ). 定理3由定理1和定理2, 不等式(15),(17)可表示成如下算子范數形式:


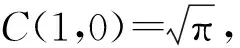
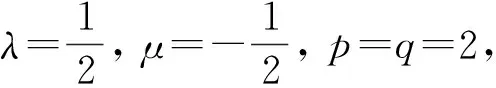




3 算子表達式