弱Galerkin有限元法的穩(wěn)定性

朱弘澤, 林 莉, 周晨光, 呂顯瑞

(吉林大學(xué) 數(shù)學(xué)學(xué)院, 長春 130012)

0 引 言

弱Galerkin有限元方法是求解偏微分方程的一種新型數(shù)值方法[1-2], 其基本思路是先用一種新定義的弱函數(shù)構(gòu)造有限元空間, 該弱函數(shù)分別定義在空間區(qū)域每個剖分單元的內(nèi)部和邊界上, 然后在弱函數(shù)空間上定義離散弱梯度算子. 從而使有限維離散弱函數(shù)空間的選取比標準有限元方法更靈活, 并且對單元剖分的要求也減弱了. 目前該方法廣泛應(yīng)用于諸多領(lǐng)域, 如Stokes方程[3]、 Biharmonic方程[4]、 Mawell方程[5]、 Brinkman模型[6]、 混合弱Galerkin有限元法[7]、 有隨機跳躍系數(shù)的弱Galerkin有限元方法[8]以及隨機偏微分方程[9]等.

本文考慮弱Galerkin有限元法求解橢圓方程的穩(wěn)定性. 設(shè)Ω為d(d=2,3)中的一個有界區(qū)域,Δ為Laplace算子, 考慮齊次Dirichlet邊值問題:

若f∈L2, 則有如下穩(wěn)定性: ‖u‖2≤C‖f‖. 特別地, 當(dāng)f∈H-1時, 由文獻[10], 有‖u‖1≤C‖f‖-1.

1 離散弱函數(shù)空間和離散弱梯度算子

設(shè)Th是Ω上的一族任意形狀的正則剖分,T∈Th是任意剖分單元, 其邊界記為?T, 直徑記為hT. 設(shè)Pk(T)是定義在T上的次數(shù)不超過k的多項式空間,Pk(?T)是定義在?T上的次數(shù)不超過k的多項式空間, 其中k為正整數(shù). 設(shè)

其中{v0,vb}|T={v0|T,vb|?T}.Vh稱為定義在剖分Th上的弱函數(shù)空間.

記(·,·)T和〈·,·〉?T分別為定義在T內(nèi)部和邊界?T上的L2內(nèi)積. ?T∈Th, 記W(T)=Vh|T為限制在每個剖分單元上的弱函數(shù)空間, 即

W(T)={u={u0,ub}:u0∈Pk(T),ub∈Pk(?T)}.

定義1離散弱梯度算子w,k-1,T:W(T)→[Pk-1(T)]d定義為

(w,k-1,Tu,q)T=-(u0,·q)T+〈ub,q·n〉?T, ?u∈W(T),q∈[Pk-1(T)]d,

(5)

其中n是邊界?T的外法向量.

下面將離散弱梯度算子的定義推廣到整個剖分Th上, 并記為w,k-1, 則?T∈Th,

(w,k-1u)|T=w,k-1,T(u|T), ?u={u0,ub}∈Vh.

在未混淆的情況下, 無論是在整個剖分還是單獨一個單元上, 下文均省略指數(shù)k-1 和T, 記離散弱梯度算子為w.

下面討論離散弱梯度算子與傳統(tǒng)梯度算子之間的差別. 設(shè)u={u0,ub}∈W(T),v={v0,vb}∈W(T), 根據(jù)弱梯度算子的定義和分部積分公式, 經(jīng)計算得

(wuh,wvh)T-(u0,v0)T=-〈(u0)·n,v0-vb〉?T-〈u0-ub,(wvh)·n〉?T,

(6)

(wuh,wvh)T-(u0,

(7)

在弱Galerkin有限元方法的定義中, 用離散弱函數(shù)空間取代經(jīng)典的函數(shù)空間, 離散弱梯度算子取代經(jīng)典變分方程中的梯度算子, 同時將式(7)右端項的變形作為補償項加入分析中, 從而得到了弱Galerkin有限元方法的變分格式.

2 求解橢圓問題弱Galerkin方法的穩(wěn)定性

得到雙線性形式為

as(v,w)=a(v,w)+s(v,w).

(8)

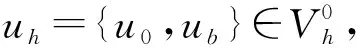
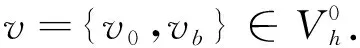
(9)

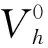
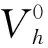
(10)

定義2對任意w∈Vh, 定義范數(shù)

(11)

其中(·,·)是區(qū)域Ω上的標準L2內(nèi)積.

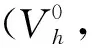
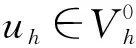
(12)

證明: 在式(9)中取v=uh, 可得

由定義2可得(Qhf,uh)≤Qhf-1uh, 故uh≤Qhf-1. 證畢.

3 求解Biharmonic方程的弱Galerkin方法的穩(wěn)定性

目前, 近似求解Biharmonic方程的有限元方法很多, 如非協(xié)調(diào)元和間斷Galerkin有限元方法[11]. 文獻[4]用弱Galerkin有限元法研究了該問題, 在H2范數(shù)下得到了最優(yōu)階誤差估計. 本文用弱Galerkin有限元方法求解Biharmonic方程的穩(wěn)定性.

考慮Biharmonic方程齊次邊值問題：

其中Δ為Laplace算子. 設(shè)k≥2, ?T∈Th, 定義T上的離散弱函數(shù)空間為

W(T)={u={u0,ub,ug}:u0∈Pk(T),ub∈Pk(?T),ug∈[Pk-1(?T)]d}.

下面將單獨一個單元上定義的離散弱空間擴展到整個剖分Th上:

定義3定義離散弱Laplace算子Δw,k-2,T:W(T)→Pk-2(T), 滿足

(Δw,k-2,Tu,φ)T=(u0,Δφ)T-〈ub,φ·n〉?T+〈ug·n,φ〉?T, ?u∈W(T),φ∈Pk-2(T).

(18)

下面將離散弱Laplace算子的定義推廣到整個剖分Th上, 記為Δw,k-2, 即?T∈Th, 有

(Δw,k-2v)|T=Δw,k-2,T(v|T), ?v∈Vh.

在未混淆的情況下, 下面省略指數(shù)k-2和T, 記離散弱Laplace算子為Δw.

設(shè)u={u0,ub,ug}∈W(T),v={v0,vb,vg}∈W(T), 利用弱Laplace算子定義和Green公式, 經(jīng)過計算得

對式(19)中右端項做如下近似:

(20)

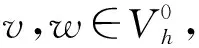
(21)

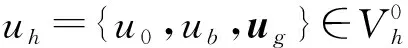
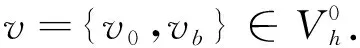
(22)

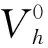
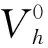
(23)

定義4對任意w∈Vh, 定義范數(shù)

(24)

其中(·,·)是區(qū)域Ω上的標準L2內(nèi)積.

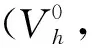
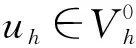
(25)

證明: 在式(22)中取v=uh, 可得

由式(24)可得(f,uh)≤Qhf-1uh, 故uh≤Qhf-1. 證畢.

綜上， 本文得到了弱Galerkin有限元方法求解Biharmonic方程的穩(wěn)定性估計.