對機械能守恒定律在解題中的應用探究

何政毅

(浙江省三門中學 318000)

“機械能守恒定律”的實質還是“能量守恒定律”，是物理力學和運動學中的特殊“能量守恒”，學習好“機械能守恒定律”對于提升我們的物理成績，促進我們的物理思想具有重要的作用，可以改變以往物理“題海戰術”的學習方法，并且讓我們的自主學習效果更高，知識應用更加靈活.

一、機械能守恒定律概述

高中物理教學中的“機械能守恒定律”主要是指“由兩個或兩個以上的物體組成的系統互相作用而遵循的一條基本能量定律.”我們知道，在高中物理的概念中，機械能是物體動能和勢能的總和，勢能可以分為重力勢能和彈性勢能.“機械能守恒定律”就是指勢能和動能在系統內進行互相轉化，其總量保持不變.如果系統的機械能初始值為E1，最終狀態的機械能值為E2，那么一定有E1=E2，即：EK1+EP1=EK2+EP2.在一個系統中，系統勢能的變化量與系統動能的變化量相等，即動能和勢能互相轉化，總體機械能不變.

二、機械能守恒定律在解題中的應用

1.單個物體的機械能守恒

這類問題一般除了重力勢能外，不計其他外來的作用，這類運動主要有：平拋類運動、懸點固定的擺動類運動、固定的光滑斜面類運動，固定的光滑圓弧類運動等.這類問題一般是物體的重力勢能和動能之間進行互相轉化，其過程可能具有一定的復雜性，但是一定遵循機械能守恒定律，通過機械能守恒定律進行分析和解答，往往可以起到良好的效果.對于單個物體的機械能守恒問題，一般是物體的動能和重力勢能進行互相轉化，與外界沒有能量交換，其表現為高度增加，速度減小，或是速度增大，高度減小.

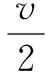
A.2 B.4 C.6 D.8

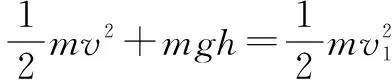
2.系統機械能守恒問題

相對于單個物體的機械能守恒，系統問題具有較強的復雜性和綜合性，這就要求我們在對系統進行分析的時候，要認真審題，進行全面的考慮，這樣才能進行問題的有效分析和解決.系統機械能守恒一般包括不計重量的連桿(輕繩)類問題、在光滑面上可以自由移動的斜面(圓弧)類問題，系統機械能守恒問題一般是單個物體機械能守恒問題的拓展和延伸，只要我們仔細的分析，正確的運用能量轉化關系，這類問題也能迎刃而解.系統機械能守恒問題一般是兩個物體或是多個物體之間通過接觸、受力等問題實現能量的轉化，需要注意的是系統機械能守恒問題分析，物體間的能量轉化沒有損失，否則不成立.

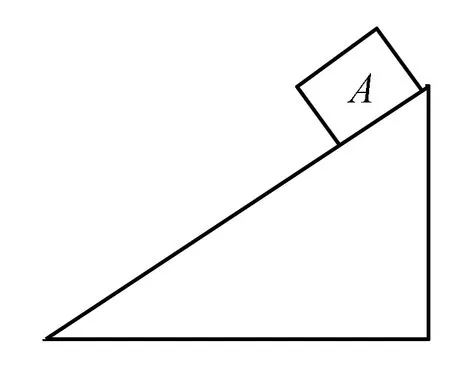
例題2 今將一個物體A放在光滑斜面的頂端(如圖所示)，斜面與物體A之間，斜面與水平面之間保持光滑，物體A由靜止開始沿斜面下滑，在物體A下滑的過程中( ).

A.斜面對物體A的力不垂直斜面，做功不為零

B.斜面對物體A的力不垂直斜面，做功為零

C.斜面對物體A的力垂直斜面，做功不為零

D.斜面對物體A的力垂直斜面，做功為零

分析本題很容易誤選D，學生一般不注意斜面與水平面光滑這一條件，以物體A的機械能守恒來進行問題的分析，從而造成了誤選.其實在本題中，物體A和斜面組成的系統機械能守恒，物體A在下滑的過程中，會對斜面做功，從而使得斜面向右運動.

三、機械能守恒定律在解題中的應用的誤區

有些物體在碰撞或是連接物體的繩子拉伸的過程中，會伴有機械能轉化為熱能的可能，因此系統的機械能不守恒，這類問題一般需要運用動量定理進行解決，運用機械能守恒定律就會出錯.因此，我們在做題的時候，要根據問題的具體情況進行判斷，不能犯這類低級的錯誤.

例題3 一質量為m的子彈，以速度v從水平方向擊中質量為M的物體，子彈沒有穿透物體，而是與物體一起在光滑的水平面上勻速向前運動，求運動的速度？

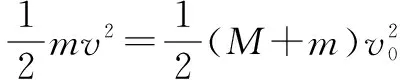
總之，“機械能守恒定律”是進行物體受力和運動分析的有效方法，對于簡化我們的思考步驟，減輕做題的運算量具有重要的作用，我們要在實際問題中進行具體的分析，以“能量守恒”為依據，弄清能量在物體間的轉化，或是同一物體上不同形態的轉化，從而有效的提高解題效率，取得一個好成績.