表面彈性對含可溶性活性劑垂直液膜排液的影響?
葉學(xué)民 李明蘭 張湘珊 李春曦
(華北電力大學(xué),電站設(shè)備狀態(tài)監(jiān)測與控制教育部重點(diǎn)實(shí)驗(yàn)室,保定 071003)(2018年5月25日收到;2018年7月3日收到修改稿)
針對含可溶性活性劑的垂直液膜排液過程,在考慮表面彈性作用的基礎(chǔ)上,采用潤滑理論建立了液膜厚度、表面速度、表面和內(nèi)部活性劑濃度的演化方程組,通過數(shù)值計(jì)算分析了表面彈性和活性劑溶解度耦合作用下的液膜演化特征.結(jié)果表明:表面彈性是影響可溶性活性劑垂直液膜排液過程中必不可少的因素.排液初期,隨表面彈性增加,液膜初始厚度增大,表面更趨于剛性化.隨排液進(jìn)行,彈性不同的液膜呈現(xiàn)不同的典型排液特征:當(dāng)彈性較小時(shí),液膜上部表面張力高,下部表面張力低,產(chǎn)生正向的馬蘭戈尼效應(yīng),與重力作用相抗衡.當(dāng)彈性較大時(shí),膜上部表面張力低,下部表面張力高,產(chǎn)生逆向的馬蘭戈尼效應(yīng),促使液膜排液加速,更易發(fā)生失穩(wěn).活性劑溶解度通過控制液膜表面的活性劑分子吸附量,進(jìn)而影響表面彈性:當(dāng)活性劑溶解度較大時(shí),液膜厚度較小,很快發(fā)生破斷;隨溶解度降低,液膜穩(wěn)定性增加,初始表面彈性也隨之增大,并隨液膜變薄逐漸接近極限膨脹彈性值.
1 引 言
表面活性劑廣泛應(yīng)用于包括鍍膜、磁流體、新生兒呼吸窘迫綜合癥表面活性劑替代療法、泡沫浮選等工業(yè)和生物醫(yī)學(xué)領(lǐng)域[1?4].其分子由親水的頭部與疏水的尾部組成,該結(jié)構(gòu)決定了活性劑更傾向于吸附在液體表面形成活性劑分子單層[5].研究表明,由于活性劑分子的結(jié)構(gòu)和特性,液滴或液膜中加入活性劑將改變表面張力,從而改變其表面彈性[6].
Gibbs彈性定義為E=dγ/d(lnA),表征對外部干擾的“抵抗”能力.對于不溶性表面活性劑,可忽略液膜表面和內(nèi)部的活性劑吸附和解吸附現(xiàn)象[7].當(dāng)表面發(fā)生擾動時(shí),一定量的活性劑分子分布在更大的面積,此時(shí)由表面活性劑質(zhì)量守恒AΓ=c可得d(lnA)=?d(lnΓ),則表面彈性隨表面張力與活性劑濃度而變化,其定義式為E=?dγ/d(lnΓ),為馬蘭戈尼(Marangoni)彈性[5].自Mysels[8]的開創(chuàng)性工作以來,多名學(xué)者對含不溶性活性劑的垂直液膜排液進(jìn)行了研究[9,10].Schwartz和Roy[11]在考慮不溶性表面活性劑的情形下,結(jié)合潤滑理論建立了兩端固定的垂直液膜排液模型,重現(xiàn)了實(shí)驗(yàn)中液膜排液過程的諸多特征,如液膜形狀和黑膜的出現(xiàn)等.Seiwert等[12]通過建立垂直液膜排液的定常偏微分方程組分析了表面彈性對提拉液膜厚度的影響,發(fā)現(xiàn)隨表面彈性與表面張力的比值E/γ增大,提拉膜厚度增加,并最終達(dá)到恒定值,此時(shí)液膜厚度與Frankel定律一致.前期本課題組先后研究了分離壓和表面黏度對垂直液膜排液過程的影響,指出分離壓與表面黏度均可增加液膜的穩(wěn)定性[13],且表面彈性在排液過程中也有較大影響.其后在考慮分離壓作用的基礎(chǔ)上,應(yīng)用潤滑理論建立了含不溶性活性劑液膜的排液模型,并分析表面彈性對液膜穩(wěn)定性的影響[14],提出排液初期增加表面彈性可提高液膜厚度,降低表面速度和促使液體逆流從而減緩排液過程.
對于垂直液膜排液過程,可溶性活性劑較不溶性活性劑的應(yīng)用更廣泛[15].當(dāng)活性劑濃度低于臨界膠束濃度(critical micelle concentration,CMC)時(shí),活性劑分子以單體形式存在于液膜表面和內(nèi)部,且二者間存在吸附和解吸附現(xiàn)象.已有研究表明,活性劑的溶解度和吸附系數(shù)均對系統(tǒng)穩(wěn)定性有重要影響[1].在數(shù)值模擬方面,Lin等[16]應(yīng)用廣義的Frumkin模型結(jié)合非線性耦合演化方程組對可溶性表面活性劑液膜穩(wěn)定性進(jìn)行研究,表明隨吸附系數(shù)Ks及內(nèi)部Peclet數(shù)的增加,表面活性劑的溶解度提高,致使膜系統(tǒng)變得不穩(wěn)定.Yiantsios和Higgins[15]在分析可溶性活性劑薄膜的馬蘭戈尼不穩(wěn)定機(jī)制時(shí),指出當(dāng)活性劑溶解度較高時(shí)系統(tǒng)穩(wěn)定性變差.而實(shí)驗(yàn)方面由于活性劑溶解度數(shù)據(jù)不易測得,因此驗(yàn)證不同溶解度的活性劑液膜穩(wěn)定性較難.史東等[17]研究陰/陽離子表面活性劑復(fù)配體系的物化性能時(shí),發(fā)現(xiàn)當(dāng)活性劑溶液出現(xiàn)網(wǎng)絡(luò)結(jié)構(gòu)的棒狀膠束、絮團(tuán)或沉淀時(shí)即達(dá)到溶解的飽和值.羅娟等[18]對聚電解質(zhì)復(fù)合物溶解性的研究表明,隨碳鏈長度增加,表面活性劑在水中的溶解度呈下降趨勢.而Bergeron[19]認(rèn)為活性劑碳鏈增加,CMC值會降低,即活性劑CMC值在一般情形下與溶解度具有一致性.
由于不同溶解度影響活性劑在液膜表面的吸附量,因此對于彈性的定義更為復(fù)雜,目前已提出多種見解.Monroy等[20]認(rèn)為受液體內(nèi)部膨脹和擴(kuò)散效應(yīng)的強(qiáng)耦合作用,表面膨脹模量在可溶性活性劑溶液中起重要作用,并用激勵毛細(xì)波技術(shù)(excited capillary waves technique)測得陽離子表面活性劑溶液的膨脹黏彈性,發(fā)現(xiàn)膨脹黏彈性隨表面活性劑鏈長和內(nèi)部濃度的增加而提高.當(dāng)壓縮頻率較低時(shí),表面與內(nèi)部活性劑總能達(dá)到平衡;頻率較高時(shí),接近不溶性活性劑情形.Lucassen和Tempel[21]首次提出膨脹彈性與振蕩頻率和活性劑濃度的表達(dá)式:式中ε0為振蕩頻率較高時(shí)的膨脹彈性,此時(shí)表面活性劑表現(xiàn)為不溶性質(zhì).Santini等[22]采用兩種不同振蕩液滴張力計(jì)測量了較大范圍的頻率值對非離子表面活性劑溶液的膨脹黏彈性的影響,表明低頻時(shí)內(nèi)部活性劑濃度越高,活性劑吸附量越大,將顯著降低表面張力梯度,則表面彈性越小.高頻時(shí)彈性隨表面吸附量增加而提高,與Beneventi等[23]觀點(diǎn)一致.
Georgieva等[24]通過測量表面張力變化研究表面膨脹彈性,提出活性劑為不溶性分子時(shí),Gibbs彈性為EG=?dγ/d(lnΓ);當(dāng)活性劑可溶時(shí),用Gibbs吸附方程可計(jì)算表面活性劑濃度與內(nèi)部濃度的關(guān)系:Wang和Yong[25,26]利用薄膜壓力平衡(thin film pressure balance)技術(shù)研究液膜排液穩(wěn)定性時(shí)定義了可溶性活性劑溶液的表面彈性為式中R為氣體常數(shù),T為絕對溫度,H為液膜厚度.Lucassen-Reynders等[7]在測量與Gibbs彈性接近的表面膨脹模量時(shí),提出EG與極限膨脹彈性ε0(不溶性活性劑彈性)關(guān)系式為且認(rèn)為活性劑濃度較低時(shí),EG接近ε0,dc/dΓ可變?yōu)閏/Γ,ε0隨表面活性劑的種類和濃度不同發(fā)生改變.
此外,Karakashev和Ivanova[27]對比了含離子與非離子型活性劑的薄液膜排液速率,指出表面彈性對表面速度的影響較大,控制液膜表面的流動性可促使液膜剛性化.Champougny等[28]用Langmuir槽法測量了不同濃度(均高于CMC)的C12E6活性劑溶液的表面彈性,表明隨活性劑濃度增加,彈性值降低,對應(yīng)的提拉液膜初始厚度也隨之減小.Seiwert和Cantat[29]假定膜厚方向活性劑濃度均勻且表面和內(nèi)部活性劑濃度相互平衡,在忽略重力情形下,建立了關(guān)于液膜厚度、表面速度和表面及內(nèi)部活性劑濃度的定常偏微分方程組,分析了活性劑特性對提拉液膜厚度的影響及與Frankel定律的差別.發(fā)現(xiàn)α(α=rmcCMC/ΓCMC)較大時(shí),活性劑溶解度提高,內(nèi)部活性劑濃度變得不可忽略,表面張力變化較小,此時(shí)可認(rèn)為表面彈性E較小,液膜厚度偏離Frankel定律較多.
綜上所述,表面彈性和溶解度是影響可溶性活性劑液膜排液過程極其重要的因素,但由于活性劑分子在液膜表面與內(nèi)部的擴(kuò)散能力以及不同溶解度活性劑在液膜表面的吸附量對表面張力梯度影響較大,使得表面彈性對排液的影響在理論上研究較為復(fù)雜.前人研究多集中在實(shí)驗(yàn)方面,尚缺乏理論上的深刻認(rèn)識.且對含可溶性活性劑液膜的研究多為固體基底的液膜,而非懸垂液膜的排液過程.為此,本文在考慮液膜含可溶性活性劑的基礎(chǔ)上,建立垂直液膜排液模型,分析表面彈性和溶解度對排液過程的作用,揭示垂直液膜排液過程的內(nèi)在機(jī)理,進(jìn)而豐富泡沫穩(wěn)定性的理論研究.
2 理論模型
圖1為頂端固定,底端與活性劑溶液池相連的垂直液膜流動示意圖.可溶性表面活性劑分布在整個(gè)液膜,假設(shè)液體為不可壓縮流體,忽略表面蒸發(fā)對排液過程的影響.液膜初始厚度為y=±h(x,t),且關(guān)于y=0對稱,因此只需考慮y>0一側(cè)液膜演化過程即可.

圖1 垂直液膜排液過程示意圖Fig.1.Schematic diagram of a vertical film drainage.
2.1 控制方程
控制方程包括連續(xù)性方程和運(yùn)動方程:

式中ρ,p,μ,g分別為液體的密度、壓力、動力黏度和重力加速度;下角標(biāo)代表對該變量求偏導(dǎo)(下同).
邊界條件為

在自由界面y=h(x,t)處,滿足動力學(xué)邊界條件和應(yīng)力平衡邊界條件:

式中,n和τ分別為液膜表面處的單位法向矢量和切向矢量;T為應(yīng)力張量,其一般形式為T=?pI+μ(?υ+?υτ),其中I為單位張量;上標(biāo)s代表液膜表面;H和γ分別是液膜表面曲率和張力;υ=(u,w);κs和μs分別代表液膜表面膨脹黏度和剪切黏度;?和?2分別代表哈密爾頓算子和拉普拉斯算子.
為簡化模型,假定表面張力與活性劑濃度為線性關(guān)系[28],即
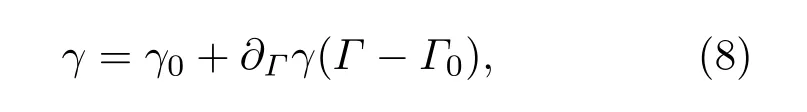
式中?Γγ為表面張力隨活性劑濃度變化曲線的斜率,γ0為初始表面張力,Γ0為初始活性劑濃度.定義表面彈性E=?Γ0?Γγ,則(8)式可變?yōu)?/p>
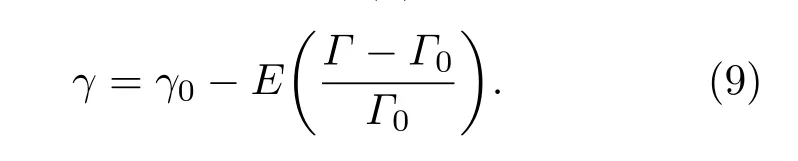
因考慮可溶性活性劑且濃度遠(yuǎn)低于CMC,則表面彈性與極限膨脹彈性ε關(guān)系為[5?7]

表面和內(nèi)部活性劑濃度的控制方程為

式中Γ和c分別為液膜表面和內(nèi)部活性劑濃度,JΓc為吸附通量,k1和k2分別為吸附率和解吸附率,Ds和Db為表面和內(nèi)部擴(kuò)散系數(shù),cs為運(yùn)動到表面處的內(nèi)部活性劑分子濃度.
2.2 無量綱化
采用如下無量綱變換式,上標(biāo)“∧”表示無量綱變量:
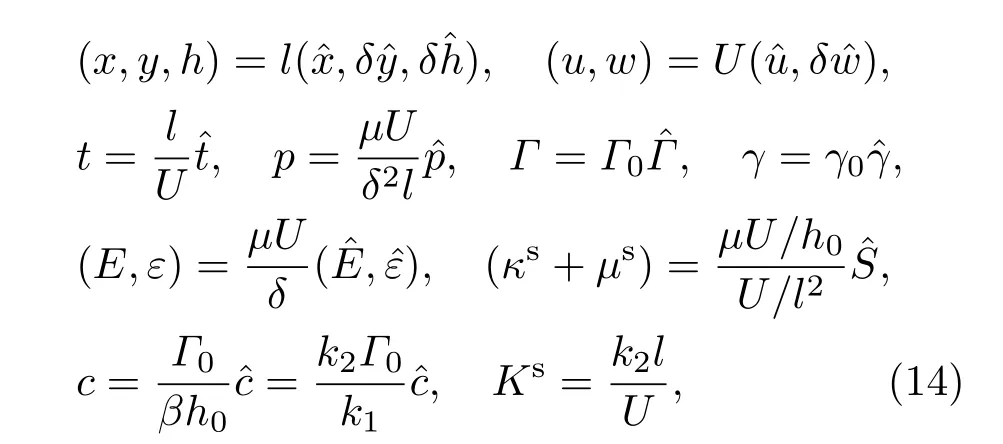
式中,δ=h0/l?1,滿足潤滑理論;h0為初始液膜厚度;l為動態(tài)彎月面長度;D為彎月面半徑,且滿足l=(h0D2)1/3;β為難溶性系數(shù),β→0,活性劑高度可溶,β→∞,接近不溶狀態(tài);特征速度
將(14)式代入(1)—(13)式中進(jìn)行無量綱化,結(jié)合潤滑理論略去二階小量.
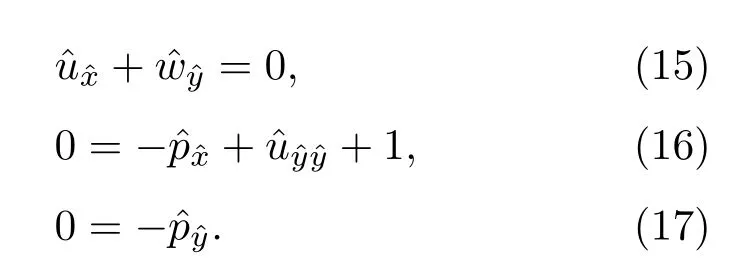
由連續(xù)性方程和運(yùn)動方程可得

由運(yùn)動學(xué)邊界條件和應(yīng)力平衡邊界條件可得由可溶性活性劑表面彈性和極限膨脹彈性關(guān)系式可得

由表面和內(nèi)部活性劑濃度可得
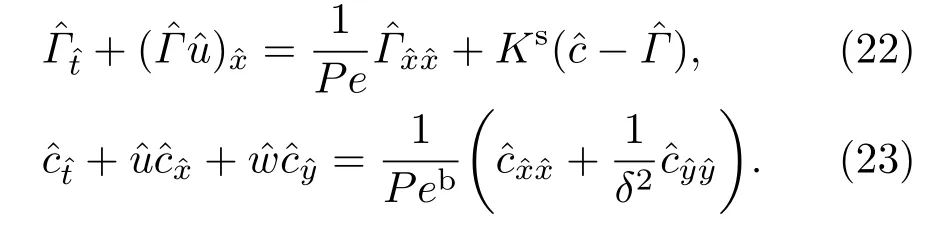
對內(nèi)部活性劑濃度,假設(shè)活性劑在垂直流動方向上擴(kuò)散速度很快[30],即該方向濃度幾乎無變化,可將c分解為平均量c1和很小擾動量c2,采用截面平均法,可得

經(jīng)推導(dǎo)可得液膜厚度?h,液膜表面速度?u,表面活性劑濃度?Γ和內(nèi)部活性劑濃度?c1的偏微分演化方程組為(為描述方便,省略上標(biāo)“∧”和下角標(biāo)“1”):

式中ε和β分別代表表面彈性和溶解度的影響,即排液過程將受上述因素的影響或控制.將(25)式去掉非定常項(xiàng)ht和重力項(xiàng)(1/12h3)x,(26)式中去掉重力項(xiàng)1/2h后,并將β設(shè)置為無窮大,吸附系數(shù)Ks設(shè)置為0,即可簡化成Seiwert等[12]所給不溶性活性劑垂直液膜排液模型.若只將β設(shè)置為無窮大,吸附系數(shù)Ks設(shè)置為0,也可簡化為本課題組前期提出的不溶性活性劑垂直液膜排液模型[14].(27)式中Ks(c?Γ)為無量綱活性劑吸附通量,下文中用JΓc表示.
2.3 邊界條件
液膜頂端(x=0)固定在框架上,液膜厚度恒定,且無液體流動,
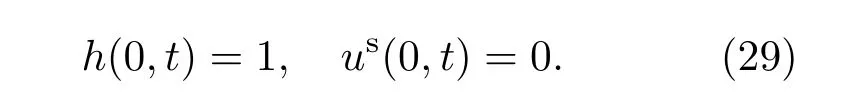
液膜底端(x=L)與液池相連接,并形成彎月面,由Young-Laplace方程[31]可知,該處液膜厚度的一階及二階導(dǎo)數(shù)滿足
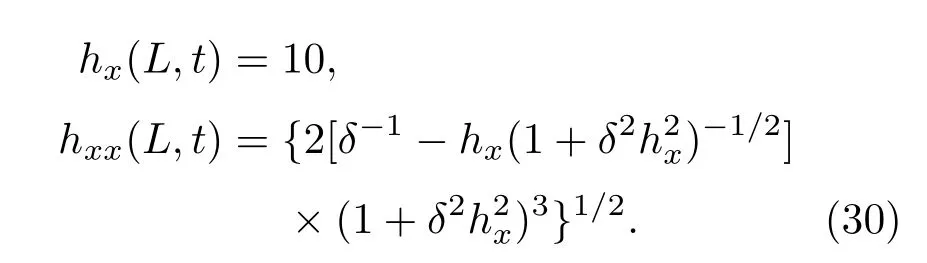
頂端無表面活性劑流動,
2.4 初始條件
液膜厚度和活性劑濃度初始條件為

式中m0=0.5,m1=1.0.
3 數(shù)值模擬
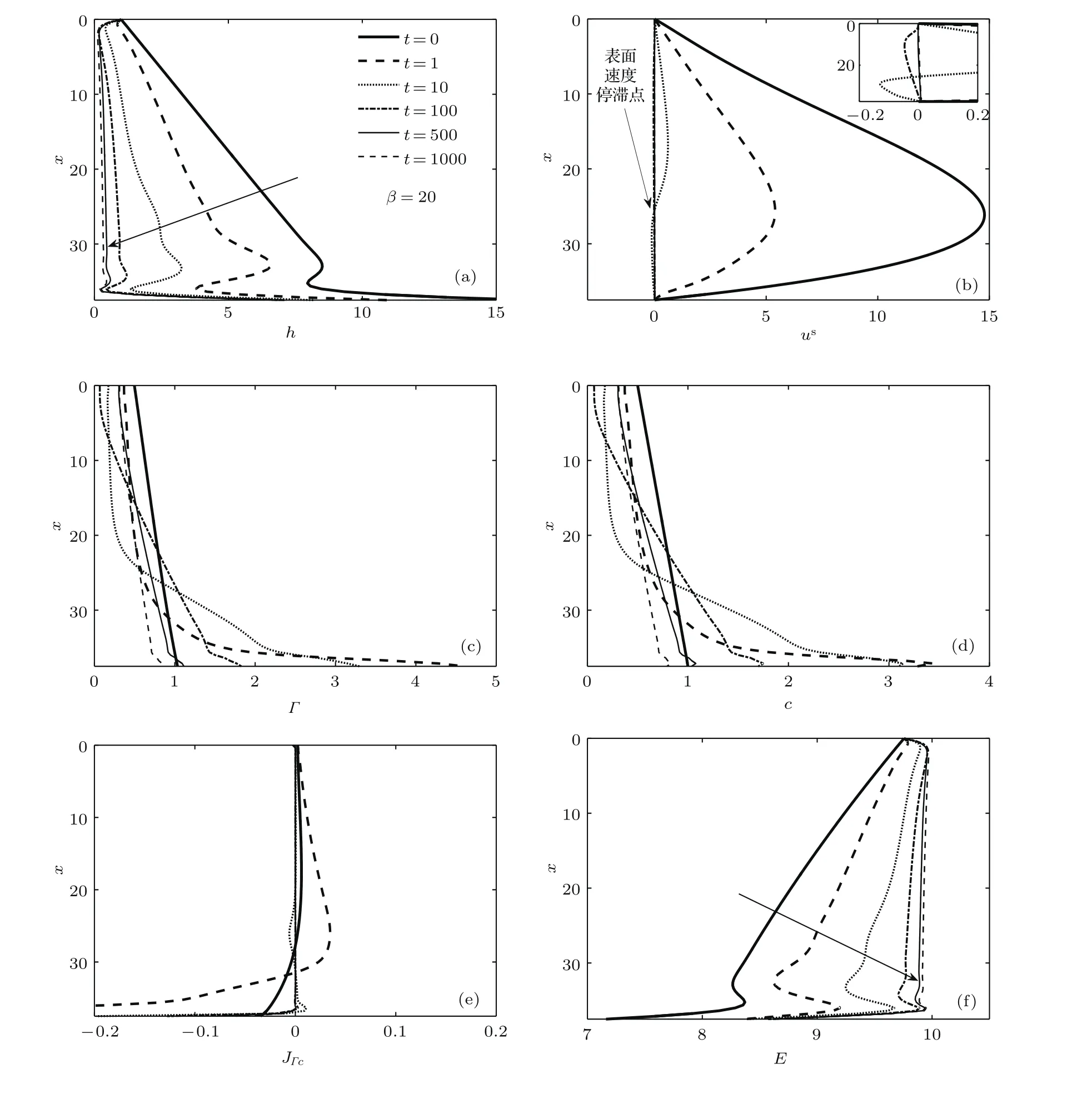
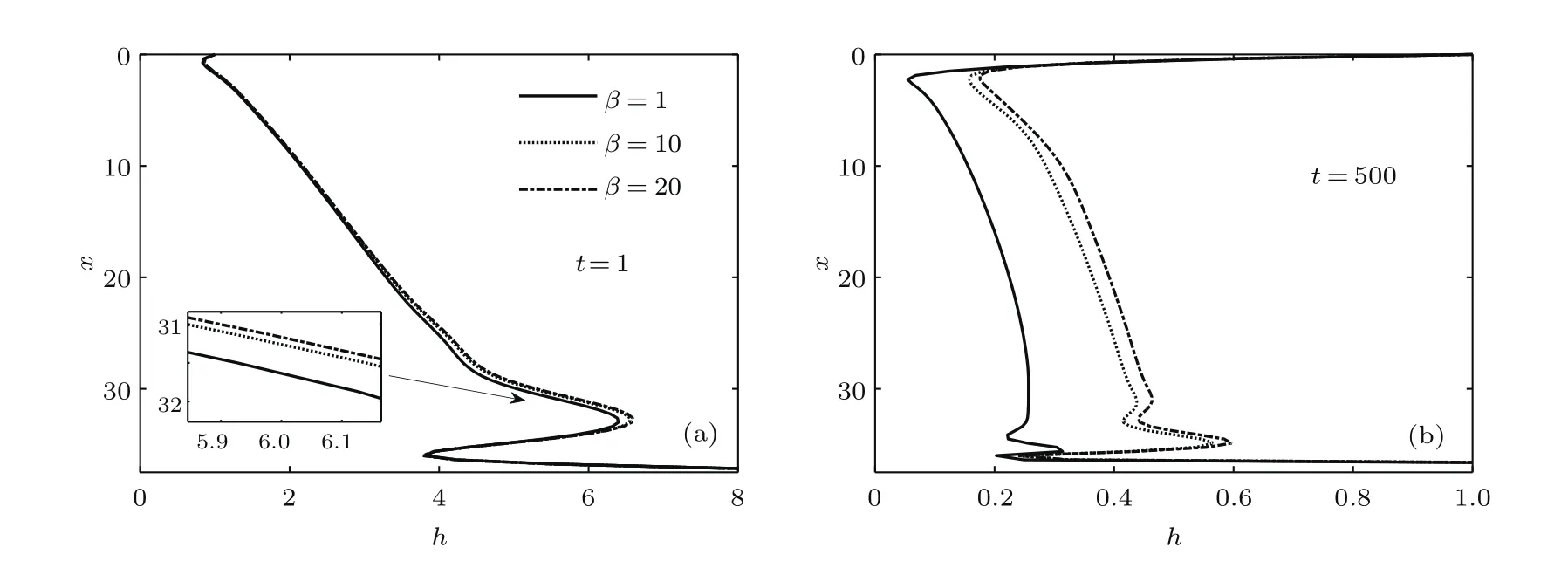
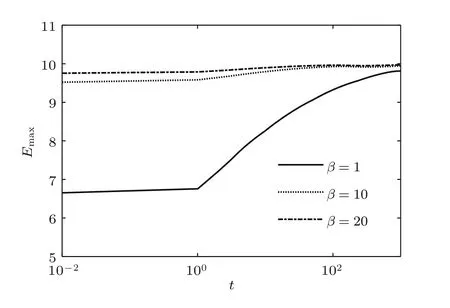
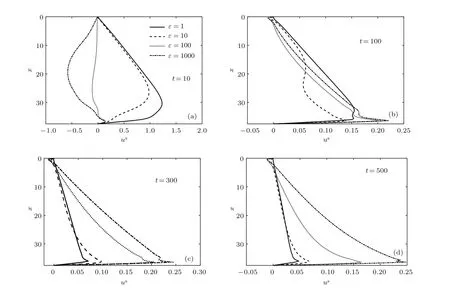
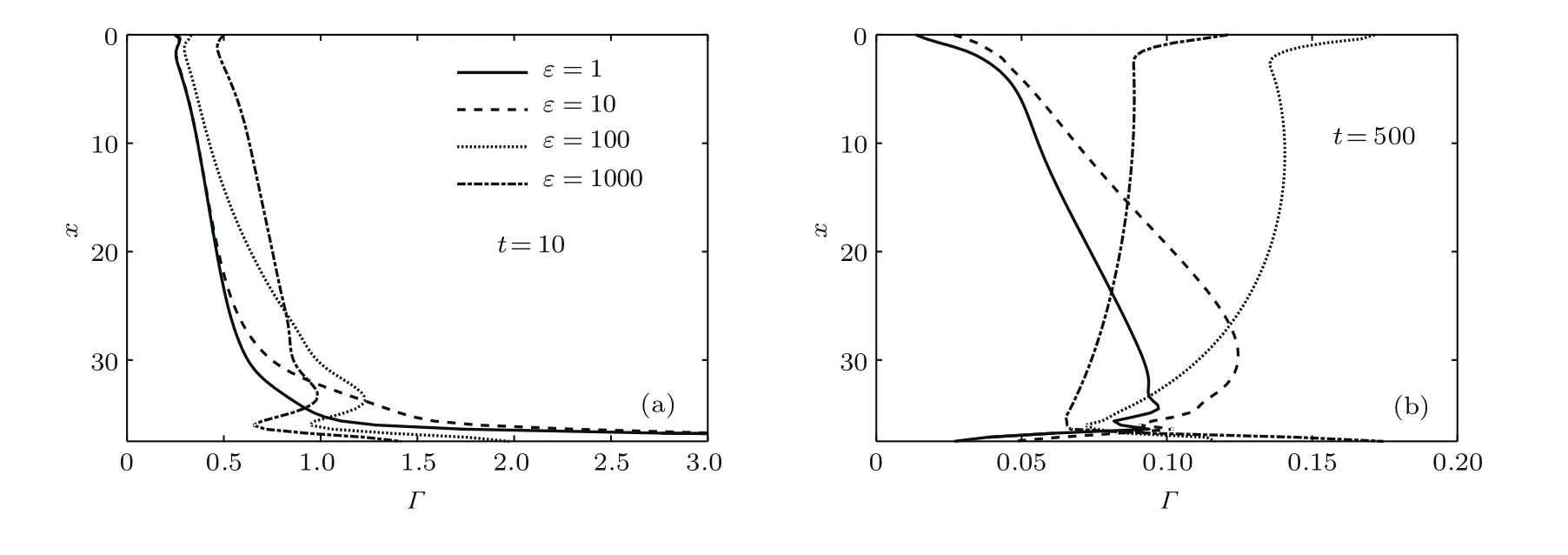
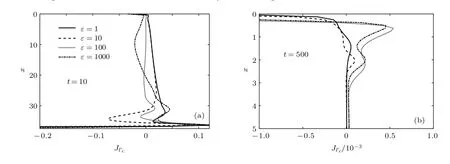
采用FreeFem程序求解演化方程組(25)—(28)式,根據(jù)液膜流動尺度選取0 表1 典型尺度及無量綱參數(shù)范圍Table 1.Typical scale and dimensionless parameters in experiments. 本文考慮表面彈性對可溶性活性劑垂直液膜排液過程的影響,且(21)式表明表面彈性由液膜厚度、極限膨脹彈性、溶解度和濃度控制.由此,溶解度和極限膨脹彈性在垂直液膜排液過程中的耦合作用不可或缺,下文首先對不同溶解度的液膜進(jìn)行分析,然后再考慮一般溶解度時(shí)極限膨脹彈性對排液的影響. 本節(jié)首先給出難溶性系數(shù)β=20,吸附系數(shù)Ks=1,極限膨脹彈性ε=10,表面和內(nèi)部Pelect數(shù)分別取Pe=100,Peb=100的液膜排液演化特征.然后分析β取不同值時(shí)溶解度對液膜排液影響,如無特殊說明其余參數(shù)保持不變. 圖2為難溶性系數(shù)β=20,吸附系數(shù)Ks=1時(shí)(活性劑溶解度較低,表面與內(nèi)部活性劑濃度較快達(dá)到平衡)的垂直液膜排液特征.排液初期,由于重力作用較大,液膜迅速變薄(圖2(a)),并產(chǎn)生4個(gè)排液特征區(qū):1)液膜頂端固定在固體線框,且滿足Young-Laplace方程[31],由此產(chǎn)生一彎月面;2)中間區(qū)域液膜較平滑,曲率幾乎為零;3)在液膜底端,液體在重力、表面張力及毛細(xì)抽吸等相互作用下發(fā)生振蕩而產(chǎn)生毛細(xì)波[33];4)與液池相連處同樣形成一彎月面.此時(shí)表面速度較大(圖2(b)),流體帶動表面活性劑流向底端(圖2(c)和圖2(d)).t=1時(shí),活性劑在液膜表面的底部囤積,并在x=30以下發(fā)生活性劑解吸附現(xiàn)象,而上部由于活性劑濃度降低,液膜內(nèi)部活性劑吸附到表面,促使液膜表面和內(nèi)部活性劑濃度再次達(dá)到平衡(圖2(e)).活性劑重新分布致使液膜上部表面張力大,下部表面張力小,由此產(chǎn)生與重力相反的馬蘭戈尼效應(yīng).隨演化進(jìn)行,馬蘭戈尼效應(yīng)逐漸增強(qiáng),表面速度不斷降低,并在t=10時(shí)出現(xiàn)表面速度停滯點(diǎn)(圖2(b)).停滯點(diǎn)下部,馬蘭戈尼效應(yīng)強(qiáng)于重力作用,表面速度為負(fù)值,出現(xiàn)逆流現(xiàn)象,停滯點(diǎn)上部重力仍占主要作用.而在t=100時(shí),幾乎整個(gè)液膜表面速度均為負(fù)值.Langevin[6]指出對于含可溶性表面活性劑的液膜排液過程,較薄液膜比較厚液膜的彈性更大,這與圖2(f)中的特征一致. 為進(jìn)一步研究具有不同溶解度的表面活性劑的液膜演化特征,圖3和圖4顯示了β=1,10,20時(shí)在典型時(shí)刻下的液膜厚度和表面速度.β=1時(shí),活性劑溶解度較高,液膜排液最快;β=10和20時(shí),液膜更易發(fā)生逆流,液膜存續(xù)時(shí)間較長.圖5為β=1,10,20時(shí)表面彈性隨時(shí)間的變化,液膜排液初期(t61),表面彈性幾乎保持不變,活性劑溶解度越低,初始表面彈性值越大.隨排液進(jìn)行,彈性均逐漸增大并最終無限接近極限膨脹彈性值ε.由上述可知,β值增加,活性劑溶解度降低,初始表面彈性和液膜厚度隨之增大,表面速度降低,液膜穩(wěn)定性提高. 圖2 液膜排液特征 (a)液膜厚度;(b)表面速度;(c)表面活性劑濃度;(d)內(nèi)部活性劑濃度;(e)吸附通量;(f)表面彈性Fig.2.Characteristics of film drainage:(a)Film thickness;(b)surface velocity;(c)surfactant concentration at the surface;(d)surfactant concentration in the film;(e)the adsorption-desorption flux;(f)surface elasticity. 圖3 不同β值時(shí)初期和后期液膜厚度對比Fig.3.Film thickness at the early and late stages of evolution at different β values. Saulnier等[34]選用兩種非離子表面活性劑C12E6和β-C12G2進(jìn)行垂直液膜排液實(shí)驗(yàn),并驗(yàn)證兩種活性劑溶液產(chǎn)生的薄膜穩(wěn)定性. 結(jié)果表明,在毛細(xì)數(shù)為10?6—10?4范圍內(nèi),兩種活性劑薄膜排液時(shí)間相差無幾,但破裂前C12E6薄膜厚度為80 nm,β-C12G2薄膜厚度為20 nm. Angarska等[35]同樣研究了C12E6和β-C12G2不同比例時(shí)混合溶液產(chǎn)生泡沫膜的穩(wěn)定性,表明在1 CMC濃度,薄膜半徑為0.05 mm限定范圍內(nèi),β-C12G2:C12E6=50:1配比時(shí)的泡沫變薄速率α(lnh=lnh0?αt)為0.036 m/s,而β-C12G2:C12E6=1:1時(shí)變薄速率為0.028 m/s.由表2可知C12E6和β-C12G2的難溶度數(shù)據(jù)分別為0.1和0.0018 m,即C12E6較β-C12G2更難溶于水,兩實(shí)驗(yàn)均證實(shí)含C12E6的薄膜比含β-C12G2的更穩(wěn)定.另外,Santini等[22]通過實(shí)驗(yàn)證實(shí)了含β-C12G2比含C10E4的泡沫膜更穩(wěn)定,即活性劑溶解度降低,系統(tǒng)穩(wěn)定性提高.Bergeron[19]用開放型探針和HBM型傳感器測得陽離子表面活性劑CnTAB,n=10,12,14時(shí)CMC值分別為70,20,4 mmol/L,通過測得的表面張力和活性劑濃度關(guān)系計(jì)算表面彈性分別為45,47,61 mN/m,并測量其對應(yīng)的分離壓.結(jié)果表明碳鏈長度增加有利于提高系統(tǒng)穩(wěn)定性,活性劑CMC與溶解度具有良好的一致性[17,18,36,37],進(jìn)一步證實(shí)了隨活性劑溶解度降低,初始表面彈性增大、系統(tǒng)穩(wěn)定性提高,并與本文所得結(jié)論一致. 圖4 不同β值時(shí)初期和后期表面速度對比Fig.4.Film velocity at the early and late stages of evolution at different β values. 圖5 不同β值時(shí)最大表面彈性的變化Fig.5.Variation of maximum elasticity at different βvalues. 表2 某些非離子活性劑的吸附速率參數(shù)Table 2.Adsorption rate parameters of some nonionic surfactants. 本節(jié)首先給出難溶性系數(shù)β=1,吸附系數(shù)Ks=1,極限膨脹彈性ε=10,表面和內(nèi)部Pelect數(shù)分別取Pe=100,Peb=100的液膜排液演化特征.然后分析ε取不同值時(shí),極限膨脹彈性對液膜排液影響,如無特殊說明其余參數(shù)保持不變. 圖6給出了極限膨脹彈性ε=10時(shí)的排液演化過程.演化初期,表面速度較大,流體在重力作用下迅速向下排液,并帶動活性劑流向底端,形成的表面張力梯度產(chǎn)生馬蘭戈尼效應(yīng)將弱化重力作用,使表面速度不斷減小,液膜逐漸達(dá)到剛性化(圖6(b)).t=1時(shí),液膜中上部分表面活性劑濃度低于內(nèi)部濃度,內(nèi)部活性劑分子吸附到表面,吸附通量為正值.而底部濃度分別為Γ=5.6,c=1.4,活性劑分子在表面的囤積促使活性劑解吸附現(xiàn)象發(fā)生,此時(shí)吸附通量為負(fù)值(圖6(e)).活性劑分子在內(nèi)部與表面的交換和內(nèi)部流體攜活性劑匯入液池的協(xié)同作用使活性劑濃度及其梯度不斷降低,因而馬蘭戈尼效應(yīng)弱于重力作用,活性劑幾乎無法發(fā)生逆流現(xiàn)象.表面彈性E隨排液進(jìn)行不斷增大,但因溶解度略高,其值始終低于β=20時(shí)的彈性值(圖6(f)和圖2(f)). 圖6 液膜排液特征 (a)液膜厚度;(b)表面速度;(c)表面活性劑濃度;(d)內(nèi)部活性劑濃度;(e)吸附通量;(f)表面彈性Fig.6.Characteristics of film drainage:(a)Film thickness;(b)surface velocity;(c)surfactant concentration at the surface;(d)surfactant concentration in the film;(e)the adsorption-desorption flux;(f)surface elasticity. 圖7為不同位置處的液膜厚度演化特征.從圖7可看出,初期排液較快,在表面達(dá)到剛性化后,液膜上部出現(xiàn)黑膜,厚度幾乎不再發(fā)生變化,并隨時(shí)間不斷向下延伸.Berg等[40]將線粗4 mm的金屬框以1.6 mm/s的速度從含有2%十二烷基硫酸鈉(sodium dodecyl sulfate,SDS)和4%甘油的混合溶液池提出,并測量提拉膜中間部位的液膜厚度.用本文(14)式對其實(shí)驗(yàn)所得隨時(shí)間演化的液膜厚度進(jìn)行無量綱化,并與本文模擬結(jié)果進(jìn)行對比(如圖7(b)所示).實(shí)驗(yàn)所得排液時(shí)間無量綱化為1.2×103,與本文排液時(shí)間保持在同一個(gè)量級,且實(shí)驗(yàn)值與模擬結(jié)果變化趨勢相同,但實(shí)驗(yàn)所得黑膜厚度較小.其原因之一是實(shí)際液膜排液時(shí)黑膜厚度h?與初始厚度h0比值過小,如按真實(shí)比例選取δ,則計(jì)算過程耗時(shí)過長,因此模擬中對無量綱液膜厚度進(jìn)行了適度放大. 圖7 特征位置處液膜厚度演化過程Fig.7.Evolution of film thickness at typical position. 由圖8可知,隨ε值增大,液膜表面彈性也隨之增加,即不同ε值的液膜排液特征與表面彈性對液膜排液的影響具有一致性.為進(jìn)一步研究表面彈性對可溶性活性劑液膜排液過程的影響,圖9和圖10顯示了極限膨脹彈性ε取值不同時(shí)在典型時(shí)刻下的液膜厚度和表面速度.由圖9可知,t=10時(shí),與ε=1,10,100,1000相對應(yīng)的液膜厚度依次增加,表面速度依次降低;且ε=100,1000情形下的液膜出現(xiàn)逆流現(xiàn)象,彈性值越大,逆流現(xiàn)象越明顯.在t=100前液膜始終保持隨ε增大,厚度增加、表面速度降低的特征.此時(shí)彈性較小的液膜流動性更強(qiáng),表面活性劑迅速流向底端,活性劑吸附和解吸附現(xiàn)象更明顯(圖11(a)和圖12(a)). 圖8 不同極限膨脹彈性值時(shí)液膜表面彈性對比Fig.8.Surface elasticity of evolution at different ε values. 而當(dāng)t>100時(shí),液膜排液便不再遵循上述規(guī)律.此時(shí)較大彈性(ε=100,1000)與較小彈性(ε=1,10)的液膜具有不同的排液特征:彈性較小時(shí),液膜始終未發(fā)生逆流.當(dāng)t=500,x>30時(shí),ε=10的液膜表面活性劑濃度及梯度均較大(圖11(b)),正向的馬蘭戈尼效應(yīng)略強(qiáng),此時(shí)液膜厚度較ε=1更厚(圖9(d)),表面速度較小(圖10(d)).x<30時(shí),ε=10的液膜表面活性劑濃度梯度與上部相反,因而表面速度略大于ε=1的液膜表面,液膜厚度在x=30附近出現(xiàn)較大差值.而當(dāng)彈性較大時(shí),排液后期液膜上部活性劑吸附現(xiàn)象更明顯(圖12(b)).此時(shí)由于上部活性劑分子從液膜內(nèi)部吸附至表面,底部活性劑分子由表面解吸附至內(nèi)部,致使液膜上部活性劑濃度較高,下部較低(圖11(d)),產(chǎn)生逆向的馬蘭戈尼效應(yīng),促使液膜向下排液.此時(shí),ε=100,1000比ε=1,10排液速率更快,液膜更薄(圖9(d)和圖10(d)).因ε=1000比ε=100的液膜濃度低,表面吸附量較少,液膜排液更為迅速.由此可知排液初期隨表面彈性增加,液膜厚度增大,流動性減弱;但排液后期較大彈性值的液膜因產(chǎn)生逆向的馬蘭戈尼效應(yīng),排液更快,液膜穩(wěn)定性降低. 圖9 不同極限膨脹彈性值時(shí)液膜厚度演化過程Fig.9.Film thickness of evolution at different ε values. 圖10 不同極限膨脹彈性值時(shí)表面速度演化過程Fig.10.Surface velocity of evolution at different ε values. Langevin[6]指出含可溶性活性劑的較薄液膜比較厚液膜的彈性更大,且對擾動的阻力更小,與不溶性活性劑特征相反.Karakashev和Nguyen[41]用Scheludko電池裝置對不同濃度的SDS(CMC為7.5mmol/L)和十二烷醇(dodecanol)的混合溶液產(chǎn)生的水平薄液膜進(jìn)行排液實(shí)驗(yàn),并通過測量表面活性劑吸附量計(jì)算表面張力與表面彈性.發(fā)現(xiàn)3.5 mmol/L SDS+10 mg dodecanol和7 mmol/L SDS+20 mg dodecanol的液膜表面彈性分別為52.1和81.6 mN/m,排液進(jìn)行到第12 s時(shí),前者液膜厚度約為29 nm,后者液膜厚度約為30 nm,而后期液膜分別于27和23 s破裂,破裂前的厚度為22和17 nm.Wang和Yoon[25]分別將加入5×10?5mmol/L的NaCl的甲基異丁基甲醇(MIBC)和聚丙二醇(PPG-400)的容量瓶搖動后產(chǎn)生大量泡沫.并通過測量表面活性劑濃度和臨界液膜厚度計(jì)算彈性值.發(fā)現(xiàn)當(dāng)表面張力為63 mN/m時(shí),二者的表面彈性分別為12和200 mN/m,平衡時(shí)液膜厚度為110和100 nm,泡沫存續(xù)時(shí)間分別為7和3 s,進(jìn)一步證實(shí)了可溶性活性劑彈性越大,排液后期液膜更容易失穩(wěn),這與圖9呈現(xiàn)的特征一致. 圖11 不同極限膨脹彈性值時(shí)初期和后期表面活性劑濃度對比Fig.11.Surfactant concentration at the early and late stages of evolution at different ε values. 圖12 不同極限膨脹彈性值時(shí)初期和后期吸附通量對比Fig.12.Adsorption-desorption flux at the early and late stages of evolution at different ε values. 圖13 ε=10時(shí)可溶性活性劑與不溶性活性劑對比 (a)液膜厚度;(b)表面速度Fig.13.Evolution of soluble surfactant and insoluble surfactant film at ε=10:(a)Film thickness;(b)surface velocity. 因前人所用實(shí)驗(yàn)方法及彈性計(jì)算公式各不相同,且實(shí)驗(yàn)中所用不同活性劑特性有很大差別,如活性劑分子結(jié)構(gòu)、活性劑分子質(zhì)量及單分子面積、親水親油基種類等均對液膜穩(wěn)定性有顯著影響,由此本文模擬結(jié)果只與部分實(shí)驗(yàn)結(jié)果定性一致. 圖13對比了含可溶性活性劑與不溶性活性劑兩種情形下的液膜厚度與表面速度.由圖13可知,在整個(gè)排液過程中含可溶性活性劑的液膜厚度較含不溶性的液膜厚度更小,表面速度更大,并在后期形成的黑膜更薄,且?guī)缀醪话l(fā)生逆流現(xiàn)象.上述特征與Lin等[16]所得的可溶性活性劑液膜更容易失穩(wěn)結(jié)論一致. 表面彈性是影響可溶性活性劑垂直液膜排液過程中必不可少的因素.排液初期,隨表面彈性增加,液膜初始厚度增大,表面更趨于剛性化.隨排液進(jìn)行,較大彈性的液膜與較小彈性的液膜具有不同的排液特征:當(dāng)彈性較小時(shí),活性劑分布使液膜上部表面張力較大,下部表面張力較小,產(chǎn)生正向的馬蘭戈尼效應(yīng),與重力作用相抗衡,抑制液膜排液.當(dāng)彈性較大時(shí),由于液膜上部活性劑吸附到表面與液膜下部表面活性劑解吸附到內(nèi)部的協(xié)同作用增強(qiáng),液膜下部表面張力較大,上部表面張力較小,產(chǎn)生逆向的馬蘭戈尼效應(yīng),促使液膜排液加速,液膜厚度變薄,更易發(fā)生失穩(wěn). 可溶性活性劑的溶解度不同致使液膜表面的活性劑分子吸附量有顯著差異,活性劑吸附量以及在液膜表面的分布不同產(chǎn)生不同的表面張力梯度,進(jìn)而影響表面彈性.當(dāng)活性劑溶解度較大(β→0)時(shí),液膜極不穩(wěn)定,很快發(fā)生破斷.隨溶解度降低(β增大),液膜穩(wěn)定性增加,表面速度降低,且更易發(fā)生逆流,液膜表面更傾向于剛性化.初始表面彈性也隨之增加,并隨液膜變薄逐漸接近極限膨脹彈性值.
4 模擬結(jié)果與分析
4.1 溶解度對垂直液膜排液的影響


4.2 極限膨脹彈性對垂直液膜排液影響





5 結(jié) 論

