光子與相對論麥克斯韋分布電子散射截面的蒙特卡羅計算方法?

李樹

(北京應用物理與計算數學研究所,北京 100094)(2018年5月10日收到;2018年8月16日收到修改稿)

高溫全電離等離子體的輻射輸運問題中,光子與電子的Compton散射與逆Compton散射是其中重要的特性,光子與相對論麥克斯韋電子散射的描述及截面的計算非常復雜且費時.本文提出了一種用于模擬計算光子與相對論麥克斯韋速度分布電子散射截面的蒙特卡羅計算方法.給出了各步驟的具體實現辦法,推導了對應的計算公式,研究了相對論電子速率抽樣方法,編寫了光子與相對論電子散射的微觀截面的蒙特卡羅計算程序.開展了高溫全電離等離子體中,不同能量光子與不同溫度電子散射的微觀散射截面計算和分析.模擬計算結果顯示,在電子溫度低于25 keV情況下,本文方法與多重數值積分方法的計算結果非常接近;但隨著電子溫度繼續升高,二者差異逐漸增大并較明顯,經分析,可能是本文方法目前的電子速率抽樣偏差所致,希望將來能夠找到更好的相對論電子速率抽樣方法以克服此缺陷.

1 引 言

恒星內部、慣性約束核聚變(inertial confinement fusion,ICF)聚變區、熱核裝置等高溫等離子體系統中的溫度高達上億攝氏度.在如此高溫度的環境下,輕物質完全電離,由熱輻射產生的光子能量范圍主要在103eV量級.對于完全電離的等離子體,能量為103eV量級的光子與物質(電子)之間的能量交換過程包括:軔致輻射、逆軔致吸收、Compton散射和逆Compton散射.于敏院士[1]在“高溫等離子體中物質與光之間的能量傳遞過程”一文中探討并得出結論“電子能量損失主要通過(逆)Compton散射”.因此,在研究恒星或ICF中的輻射輸運問題時,Compton及逆Compton散射問題是需要重點關注的對象.

當上述等離子體系統處于完全熱平衡態(電子、離子和輻射的溫度相同)時,電子溫度可達10 keV以上;某些情況下,系統處于非平衡態(電子、離子、輻射具有各自的溫度),電子溫度可能達到近100 keV.在此非平衡態情況下,光子與電子的相互作用不僅需考慮電子的熱運動速度,而且必需在相對論體系下考慮光子與電子的相互作用[2].

利用蒙特卡羅方法模擬高溫等離子體中的輻射輸運問題時,需要知道任意能量的光子與任意溫度電子的相互作用(吸收、散射)截面,以及發生散射后出射光子的能量和角度.本文討論光子與電子的散射截面計算問題,散射后光子和電子的能譜、角度譜計算將在后續的研究中討論.

光子與靜止自由電子發生Compton散射的微分截面Klein-Nishina公式[3]為式中re為電子經典半徑;ε為以電子靜止能量為單位的入射光子能量,即ε=hν/(m0c2),其中hν為入射光子能量,m0為靜止電子質量,c為光速(約300 cm/sh,sh是本文的時間單位,1 sh=10?8s);?為入射光子與出射光子夾角(偏轉角);?為立體角.

對(1)式關于立體角積分,得到能量為hν的光子與1個靜止自由電子發生散射的概率(微觀散射總截面)公式[4]

當ε較小時,(2)式的計算容易產生數值誤差,且該式中的對數計算較費時.故通常采用如下的Hastings[5]近似公式代替(2)式計算微觀散射總截面:

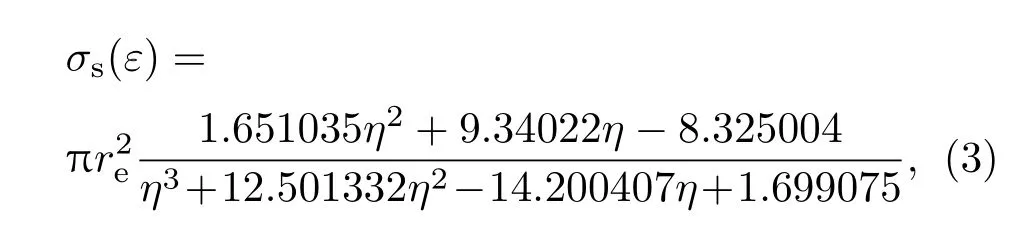
式中η= 1+0.222037ε.這 里 稱(3)式 為KNHastings公式.

在特別設定的坐標系(入射光子沿Z軸飛行、出射光子位于XZ平面)下,光子與速度分布函數為f(u)的各向同性電子發生散射的微分截面計算公式[2]為式中ν和ν′分別為入射、出射光子頻率;ζ=cos?=? ·?′為光子偏轉角余弦;u為電子速率;為電子的Lorentz因子;μ=cosα為與電子運動方向相關的第1個積分角度變量,其中α為電子運動方向與入射光子方向(Z軸)的夾

角;ε=hν/(m0c2);ε′=hν′/(m0c2);函數g(u,μ)定義為

?為電子運動的方位角.δ函數是為了滿足散射的動量守恒引入的,且僅當

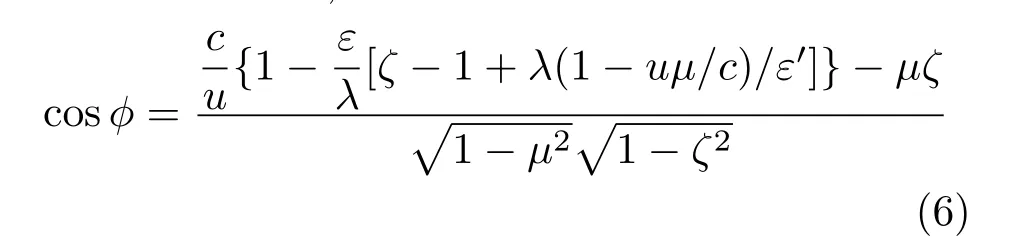
時,(5)式中的δ可以消除掉.電子速度分布f(u)可取任意概率密度函數,這里取相對論麥克斯韋-玻爾茲曼(relativistic Maxwellian-Boltzman,RMB)速度分布函數(詳見第3節).

關于(4)式的計算比較復雜,已有多篇文獻介紹如何計算該式.這些文獻[6?15]的基本思路大多是:首先將(4)式中的積分核函數展開(冪級數、勒讓得函數),然后采用多重數值積分的方法計算散射截面以及在此基礎上計算確定論輸運模擬方法[16]所需的分群能譜與角度譜、或者蒙特卡羅輸運模擬所需的散射后出射光子的能量與方向[17,18].

本文不討論數值計算(4)式,而是利用蒙特卡羅方法,首先逐個直接模擬光子與相對論電子的相互作用,得到若干光子與單個電子散射的概率值,然后取這些概率值的統計平均值,最后得到一定頻率的光子與一定溫度的電子發生散射的概率(截面).因此,本文方法的實質是利用蒙特卡羅方法計算多維復雜核函數的積分問題(注:計算散射截面為6維,計算散射后的能譜角度譜為8維).

2 光子與相對論電子散射的蒙特卡羅方法

圖1 實驗室系光子與溫度為Te的電子散射示意圖Fig.1.Photon scattering with electrons at temperature Tein lab coordinate.

問題描述:如圖1所示,設實驗室坐標系X0Y0Z0(簡稱0系)中,t時刻有一光子(hν0,?0)(光子能量和飛行方向),求其與r0處溫度為Te的電子發生散射的概率(微觀散射截面)及散射后光子和電子的能量、角度分布.由于篇幅的原因,本文只討論散射概率的計算方法,散射后光子和電子的能量、角度分布計算方法將另文討論.

蒙特卡羅求解步驟:

步驟1根據電子溫度Te抽樣單個電子狀態(u0e,?0e)(電子速率和飛行方向).其中,電子飛行方向?0e(?x0e,?y0e,?z0e)為各向同性抽樣:

式中ξ1和ξ2為[0,1]之間的隨機數.

由此可以求得光子與電子的飛行方向夾角余弦cosα0=?0·?0e.

電子速率u0e從RMB速率分布函數中抽樣得到,后面將針對此問題單獨展開討論.

入射光子與抽樣出的單個電子在實驗室系中的散射前狀態如圖2所示.

圖2 實驗室系中光子與抽樣出的單個電子散射前示意圖Fig.2.Photon scattering with the sampled electron in lab coordinate.

步驟2設置新笛卡兒坐標系X1Y1Z1(簡稱1系),其坐標原點與r0重合,X1軸正方向與電子運動方向?0e一致,Z1軸垂直于電子運動方向與光子飛行方向所組成的平面.由于0系與1系只存在平移和旋轉變換,因此在1系中,光子與X1軸(電子飛行方向)夾角α1=α0,光子在1系中的(碰撞前)狀態為

電子在1系中的(碰撞前)狀態為

入射光子與單個電子在坐標系1中的散射前狀態如圖3所示.

圖3 坐標系1中光子電子散射前示意圖Fig.3.Photon scattering with electron in coordinate 1.

步驟3建立一個隨電子運動的笛卡兒坐標系X2Y2Z2(簡稱2系).坐標系2與坐標系1在t時刻重合,運動方向為X1軸正方向,運動速度為u1e(圖4).故電子在2系中始終靜止(u2e=0)且位于坐標原點.

圖4 坐標系1與坐標系2關系示意圖Fig.4.Relationship between coordinate 1 and coordinate 2.

現求光子在2系中的狀態.根據狹義相對論,對于光子,(Px,Py,Pz,iE/c)構成一個四度向量,又因光子動量光子能量E=hν,所以,(ν?x,ν?y,ν?z,iν)亦構成四度向量.1系中的四度向量(ν1?x1,ν1?y1,ν1?z1,iν1)與運動坐標系2系中的四度向量(ν2?x2,ν2?y2,ν2?z2,iν2)可以通過Lorentz變換建立關系[19]:式中λ=[1?(u1e/c)2]?1/2.

求解(10)式后得到

代入步驟2已求得的u1e,?x1,?y1,?z1值后得到

由此計算得到光子在2系的頻率ν2及飛行方向?2(?x2,?y2,?z2),(12)式中α2是光子在2系中的飛行方向與X2軸的夾角(如圖5所示,Z1,Z2軸均垂直于紙面).

圖5 光子在1系和2系中的飛行方向與坐標軸夾角示意圖Fig.5.Photon’s flight directions and angles in coordinate 1 and coordinate 2.

步驟4建立笛卡兒坐標系X3Y3Z3(簡稱3系).Z3軸與Z2軸相同,X3軸由X2軸以Z2軸為軸旋轉角度α2得到,即X3軸與光子在2系中的飛行方向?2重合,2系與3系的關系及光子飛行方向如圖6所示,其中的Z軸重合且均垂直于紙面.由于2系與3系之間僅存在旋轉變換,故光子頻率不變,因此光子在3系中的狀態為:hν3=hν2,?x3=1,?y3=0,?z3=0.

至此,在3系中,光子與電子的相互作用圖像是:一個能量為hν3的光子沿X3軸正方向飛行,在坐標原點處與一個自由靜止的電子發生散射,如圖7所示.故可以方便地采用Klein-Nishina公式處理,這里的微觀散射總截面計算采用(3)式,式中的ε=hν3/(m0c2), 計算出的σs(ε)就是光子(hν0,?0)與相對論電子(u0e,?0e)發生散射的概率.

圖6 坐標系2與坐標系3關系示意圖Fig.6.Relationship between coordinate 2 and coordinate 3.

圖7 坐標系3中光子與電子散射示意圖Fig.7.Photon scattering with electron in coordinate 3.

上述4個步驟描述了入射光子與單個特定(抽樣出的)相對論電子的微觀散射截面計算方法.由于相對論效應引起的空間收縮,與光子飛行方向相反的電子密度比與光子飛行方向相同的電子密度高,因此,需要將截面σs(ε)乘以空間尺度變化引入的Lorentz因子[20].對于光子與溫度為Te的電子發生散射的概率,重復步驟1—步驟4若干(N)次,便可以得到N次平均的結果:

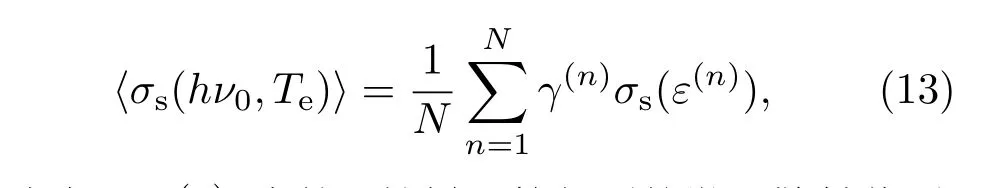
式中σs(ε(n))為第n抽樣計算得到的微觀散射截面;γ(n)為第n次抽樣計算的空間變化Lorentz因子:

式中cosα0=?0·?0e為光子與電子的飛行方向夾角余弦.

抽樣足夠多的樣本計算后,?σs(hν0,Te)?將逐漸收斂到某一固定值,該值即可認為是光子(hν0,?0)與溫度為Te的電子發生散射的概率(微觀散射截面).

分析上面的計算流程可以看出,對于散射截面,本文方法的計算精度取決于兩個因素:電子速率分布抽樣的準確性;抽樣的樣本數N(收斂性).

3 關于電子速率的抽樣

經典麥克斯韋-玻爾茲曼(classical Maxwellian-Boltzman,CMB)速率分布的概率密度函數為

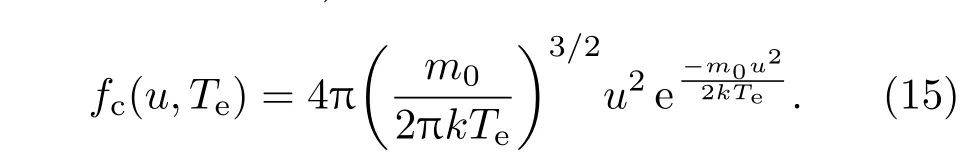
此函數的一種比較新且效率和精度均較高的抽樣方法可以參考文獻[21].

高溫全電離等離子體中,當電子達到熱力學平衡態時,溫度為Te的電子速率u服從RMB速率分布,其概率密度函數[19,22]為

式中k為玻爾茲曼常數為電子的Lorentz因子;K2(x)為二階變型貝塞爾函數:

求(16)式的積分非常困難,因此抽樣計算速率u的值很難實現.筆者也未能查閱到關于(16)式抽樣方法的相關文獻.因此,為了解決此問題,本文推導了一種近似RMB(similar relativistic Maxwellian-Boltzman,SRMB)速率分布函數:

式中β=λ?1.關于分布函數的推導及抽樣方法不是本文的重點,這里暫且不討論.

本文利用(18)式作為電子速率分布的抽樣函數分析抽樣結果.

首先,分析需要多少樣本才能使得抽樣的電子速度分布收斂.針對(18)式編制抽樣程序,計算并統計不同抽樣樣本條件下的電子速率分布.圖8給出了在電子溫度為25 keV情況下,樣本數分別為104,105和106條件下,統計平均后得到的電子速率概率密度分布及與(18)式解析計算結果的比較情況.可以看出當抽樣樣本數達到106時,抽樣統計結果與解析結果基本一致,由此可以認為結果已收斂.為了盡量排除抽樣樣本引入的誤差,后面的計算結果都是樣本數為107的情況下得到的.

圖8 三種樣本數條件下的電子速率分布及與解析結果比較(Te=25 keV)Fig.8.Electron speed distributions and analysis results with three kinds of sampled particles(Te=25 keV).

然后,分析近似(18)式抽樣的電子速率分布的準確性.這里的準確性,指的是與RMB速率分布函數(16)式的符合程度,若符合得越好,則準確性越高.圖9給出5種電子溫度(1,10,25,50和100 keV)情況下,利用近似(18)式抽樣計算得到電子速率分布(SRMB sampled),將其與(16)式的解析結果(RMB analysis)進行比較,同時圖中還給出了根據(15)式抽樣計算的電子速率分布(CMB sampled).

1)電子溫度低于10 keV情況(圖9(a)和圖9(b))下,相對論效應不明顯,利用CMB分布函數、SRMB分布函數抽樣計算得到的結果與RMB分布函數的解析結果基本一致.

2)電子溫度升高至25 keV情況(圖9(c))下,由于相對論效應,利用CMB分布函數抽樣計算得到的結果與RMB分布函數的解析結果有較明顯的差異;然而,利用SRMB分布函數抽樣計算得到的結果與RMB分布函數的解析結果仍有較好的符合度.

圖9 不同電子溫度下電子速率分布 (a)1 keV;(b)10 keV;(c)25 keV;(d)50 keV;(e)100 keVFig.9.Electron speed distributions under different electron temperatures:(a)1 keV;(b)10 keV;(c)25 keV;(d)50 keV;(e)100 keV.

3)隨著電子溫度的繼續上升 (圖9(d)和圖9(e)),CMB分布函數抽樣計算得到的結果與RMB分布函數的解析結果差異繼續增大且非常顯著;利用SRMB分布函數抽樣計算得到的結果與RMB分布函數的解析結果有差異但小于CMB抽樣結果.另外,從圖9(d)和圖9(e)可以看出,CMB分布抽樣出的電子速度有顯著超光速(c=300 cm/sh)不合理現象出現,然而,SRMB分布抽樣出的電子速度不會出現超光速現象.

綜合以上計算結果及分析,可得:樣本數106以上,抽樣計算結果基本收斂;電子溫度不超過25 keV,本文的電子速率分布抽樣較準確,電子溫度高于25 keV,偏差增大,這可能會影響到散射截面的計算精度.

4 散射截面的數值模擬結果與分析

根據本文第2節介紹的方法,研制了光子-相對論麥克斯韋電子散射模擬程序,該程序可以計算任意光子(能量范圍為0—1 MeV)與任意溫度電子(溫度范圍為0—100 keV)的微觀散射截面及散射角度譜、能譜.表1是文獻[11]中給出的利用數值積分方法計算的光子-電子散射截面.為了分析電子熱運動對散射截面影響,表2列出了利用(3)式計算的光子與靜止自由電子的散射截面;表3是利用本文方法計算的光子-電子散射截面.為了便于比較,表2和表3在給出散射截面的同時還列出了其與表1中對應值的相對誤差其中σtable1,σtable2和σtable3分別是表1、表2和

首先,分析表1可以看出:光子能量越高,截面越小;電子熱運動使得截面變小,且電子溫度越高、熱運動平均速度越大,截面減小越多.

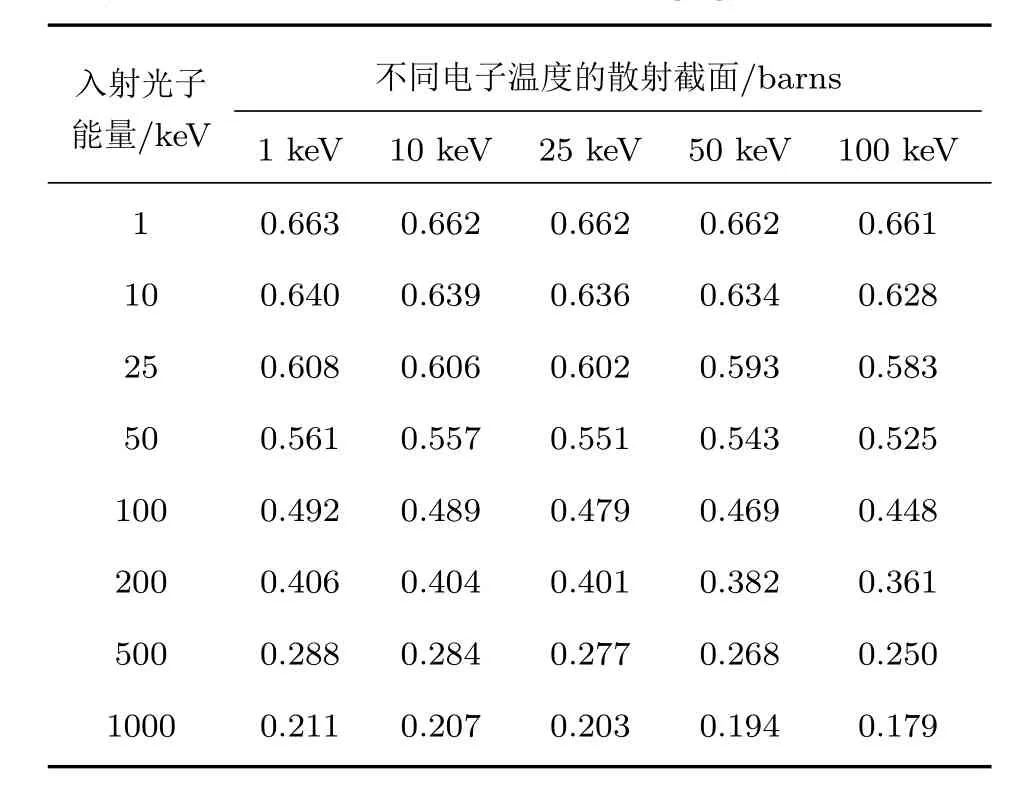
表1 光子-相對論麥克斯韋電子散射截面(文獻[11]數值積分計算)Table 1.Photon-Maxwellian electron cross-sections(numerical integration method,Ref.[11]).

表2 光子-靜止自由電子散射截面(KN-Hastings近似(3)式計算)Table 2.Photon-still free electron at rest cross-sections(KN-Hastings method,using Eq.(3)calculated).

表3 光子-相對論電子散射截面(本文蒙特卡羅方法計算)Table 3.Photon-Maxwellian electron cross-sections(proposed Monte Carlo method).

表2的截面計算因未考慮電子熱運動,故相對于表1其值偏大,且電子溫度越高,截面偏大越多;光子能量越高,截面偏大越多;例如:在光子能量為1 MeV、電子溫度為100 keV情況下,相對誤差達18%左右.

表3本文方法計算的散射截面,在電子溫度不高于25 keV情況下與表1的結果很接近,相對誤差不超過2%;但是隨著電子溫度繼續升高,偏差逐漸增大,例如:在光子能量為1 MeV、電子溫度為100 keV情況下,相對誤差也達到7.8%.

分析本文方法在電子溫度較高(>25 keV)情況下與國外的數值積分方法差異的原因:前面已經提到過,電子平均速度越大截面越小.然而,從前面的圖9(d)和圖9(e)可知,在電子溫度較高時,本文目前關于電子速率的抽樣方法抽出的電子速率整體偏小,這可能就是導致本文方法計算的散射截面偏大的原因.因此,本研究下一步將圍繞相對論電子速率的準確抽樣目標開展.

5 結 論

本文提出了一種計算光子與相對論麥克斯韋分布電子散射截面的方法.該方法的實質是利用蒙特卡羅方法計算多維復雜核函數的積分.本文方法具有如下特點:第一,在給定的光子能量范圍(0—1 MeV)和電子溫度范圍(0—100 keV)內,不需要針對光子能量和電子溫度分群離散,即可以根據單一光子能量和單一電子溫度直接計算出對應的散射截面;第二,散射后光子與電子的能量和角度是連續的,可以方便地利用蒙特卡羅方法確定(另文介紹),因此,本文方法特別適用于利用蒙特卡羅方法模擬光子在高溫等離子體中的Compton散射和逆Compton散射問題;第三,與數值積分方法計算散射截面相比,本文方法無需做復雜繁瑣的數學處理,因此更加直觀、簡潔.

本文方法在電子溫度不超過25 keV情況下的計算精度較高(注:此情況能夠滿足大多數ICF、熱核裝置等問題所需);在電子溫度更高情況下,可能是目前的電子速率抽樣有偏差的原因,導致目前的計算結果與國外多重數值積分結果存在較明顯差異;待將來找到更好的相對論電子速率抽樣方法后,此缺陷應該能夠被克服.