PGNAA方法測量元素的非線性規律研究

吳志強，龔亞林

(丹東東方測控技術有限公司，遼寧 丹東 118002)

瞬發伽瑪中子活化分析(prompt gamma neutron activation analysis, PGNAA)技術使用中子激發物料元素，并對特征伽瑪射線進行探測分析，而中子和伽馬射線均具有極強的穿透能力，可獲取大厚度物料內部全元素信息。因此，PGNAA技術樣品測量具有非接觸、非破壞性、全元素測量、實時在線分析、可穿透一定厚度的容器及物體進行分析、不受環境影響、分析精度高等特點，普遍用于工業在線檢測領域。以水泥生產、煤炭資源、冶金生產等資源消耗密集型產業的使用最具代表性。水泥、冶金行業需要在生產過程中及時掌握物料元素成分信息，以便實現生產過程的節能降耗及產品質量的有效提升；煤炭燃燒過程中，需要了解煤炭的成分信息，以便實現對煤炭使用的高效、環保。PGNAA在線分析儀可及時獲取關鍵工業物料信息，提高生產效率，實現節能降耗，促進落后產能轉變。

PGNAA在線分析儀主要有旁線式與跨皮帶式，其中跨皮帶式安裝方便、物料通過性強、維護成本低，市場應用率達到90%以上。跨皮帶式PGNAA在線分析儀在投運之前經過實驗室靜態標定、現場靜態標定和現場動態標定。這三個標定程序均基于標準物料厚度，如果厚度發生較大變化，將引起較大的測量偏差。為保證分析儀的測量準確性，通常要求皮帶上物料厚度恒定。但由于工業現場的產量變化需求，皮帶上物料不恒定，導致產量變化時在線分析儀的測量精度受到較大影響。通常在皮帶上加裝變頻器，當產量變化時，調整皮帶的轉動頻率，保證皮帶上物料的厚度不變。但加裝變頻器會增加采購成本和維護量，且長度超過1 000 m的較長皮帶很難實現變頻調速，所以工業現場并不希望加裝變頻器。如何在皮帶上物料厚度變化的環境下依然保證在線分析儀測量精度，是亟待解決的問題。為此，本研究結合理論分析和蒙卡模擬研究PGNAA測量不同厚度物料時的誤差原因，并尋求厚度修正模型，以適應工業現場產量變化時的元素檢測需求。

1 PGNAA原理與蒙特卡羅方法

瞬發伽瑪中子活化分析(PGNAA)原理圖示于圖1。當中子轟擊物料時，中子與靶核發生俘獲反應，形成復合核。中子被俘獲后，原子核處于激發態，隨即發射一個或幾個瞬發伽瑪射線，然后復合核回到基態，或變成放射性核素。瞬發伽瑪射線的能量與新形成核的中子結合能有關，所以元素放出特征能量的伽瑪射線。以探測瞬發伽瑪射線進行元素分析的方法，稱為瞬發伽瑪中子活化分析[1]。

圖1 瞬發伽瑪中子活化分析原理圖Fig.1 Schematic diagram of prompt gamma neutron activation analysis

蒙特卡羅方法又稱隨機抽樣技巧或統計試驗方法，其主要應用范圍包括：粒子輸運、統計物理、典型數學、真空技術、激光技術以及醫學、生物、探礦等方面。蒙特卡羅方法在描述粒子輸運時可以應用到實驗核物理中，主要包括：計算通量和反應率、中子探測效率、光子探測效率、光子能量沉積譜及響應函數、氣體正比計數管反沖質子譜、多次散射與通量衰減修正等。

2 理論分析

PGNAA方法伽瑪探測器收集的瞬發特征伽瑪射線的強度反映物料中元素含量[2]。當單能平行中子束照射充分薄且均勻樣品時，反應率可表達為:

R=nσφ

(1)

式中，R為反應率，s-1；n為中子束照射內原子核數目；σ為給定能量中子俘獲截面，cm2；φ為中子通量，cm-2·s-1。考慮探測器的探測效率，特征能量的特征伽瑪峰計數率可表達為：

ργ=ε(Eγ)nσγφ

(2)

式中，ργ為計數率，即凈峰面積除以測量時間；ε(Eγ)為探測器的探測效率。

但是大部分情況下中子的能量不單一，俘獲反應截面與能量相關，被照射樣品不可能達到理想的厚度，必須考慮樣品內部中子場的變化和伽瑪射線的衰減。綜合這些因素，得到：

ε′(Eγ,r)dEndr

(3)

式中，μ(r)為樣品(不均勻)內部位置r處元素的質量密度；M為元素的相對原子質量；NA為阿伏加德羅常數，6.022×1023mol；σγ(En)為與中子能量相關的特征伽瑪射線產生截面；φ′(En,r)是以樣品內部位置和能量為變量的中子通量函數(主要為樣品內部中子自屏蔽效應)；ε′(Eγ,r)是樣品內部位置的探測器對特征能量伽瑪射線的探測效率(主要為伽瑪自衰減效應)。

從公式(3)可以看出，由于物料內部對中子的自屏蔽效應和對伽瑪射線的自衰減效應[3-6]，被照射物料元素產生的特征伽瑪射線強度不可能完全隨物料的增多而線性增長。只有物料是理想情況下的足夠薄，不考慮物料自身對中子的自屏蔽效應和對伽瑪的自衰減效應時，才可以認為特征射線的強度與元素含量或物料厚度成正比。

3 蒙特卡羅模擬

3.1 模擬裝置

模擬實驗的裝置圖示于圖2。PGNAA裝置主要有中子源、慢化體、物料和伽瑪探測器等[3]。本研究模擬裝置中子源采用252Cf源。選取若干種代表性物料，包括單質：純凈Fe粉，密度為1.4 g/cm3；氧化物：純凈Al2O3、SiO2、CaO，密度分別為3.8、1.5、1.5 g/cm3；混合物料：水泥生料，密度為1.6 g/cm3。

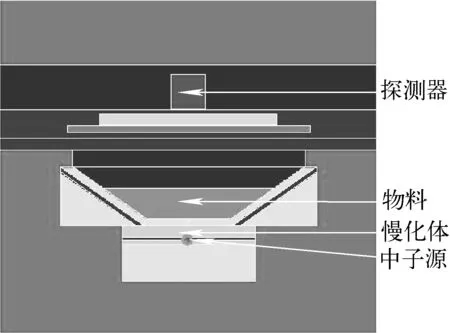
圖2 PGNAA模擬裝置示意圖Fig.2 Schematic diagram of PGNAA analog device

3.2 分析過程

252Cf中子源發射快中子，經慢化體慢化后成為熱中子，熱中子與物料中的原子核發生俘獲反應，放出特征伽瑪射線，最后被伽瑪探測器接收。

3.3 模擬結果

3.3.1不同厚度單質與氧化物

改變模擬裝置的物料種類與厚度，分別模擬計算鋁(7.73 MeV)、硅(4.93 MeV)、鈣(6.42 MeV)、鐵(7.64 MeV)特征射線計數隨物料厚度變化的情況。在中子活化元素分析儀的測量裝置內分別放入不同厚度的Al2O3、SiO2、CaO、Fe粉，測量中子活化能譜，去除本底，得到特征伽瑪射線計數。各元素特征伽瑪射線隨單質厚度的變化趨勢示于圖3，實驗測量結果與蒙特卡羅模擬結果符合很好。

從圖3結果可以看出，鋁、硅、鈣、鐵4種元素物料厚度小于8 cm時，隨著厚度增加，特征伽瑪射線計數迅速增加；但當物料厚度增加到10 cm時，隨著物料厚度的增加，鋁、硅、鈣的特征伽瑪射線計數增長率開始變小，而鐵的特征伽瑪射線計數隨物料厚度的增加下降。這種現象主要由兩種效應引起，一是隨著物料厚度增加，物料內部的熱中子被大量吸收，導致物料內部熱中子通量下降，俘獲反應的幾率相應下降，為中子自屏蔽效應；二是隨著物料厚度增加，物料下層產生的特征伽瑪射線經過上層物料的衰減后才能到達探測器，降低了特征伽瑪射線的探測效率，為伽瑪自衰減效應。這兩種效應均導致元素特征射線與物料厚度呈現非線性增長規律。模擬中，密度較大的鐵粉中子自屏蔽和伽瑪自衰減效應均強于密度較小的Al2O3、SiO2、CaO，導致鐵特征伽瑪射線計數在Fe粉厚度為8 cm時下降。

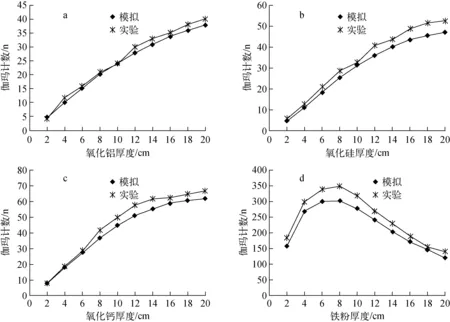
a——鋁(7.73 MeV)；b——硅(4.93 MeV)；c——鈣(6.42 MeV)；d——鐵(7.64 MeV)圖3 元素特征伽瑪射線強度與厚度關系a——Aluminum(7.73 MeV)；b——Silicon(4.93 MeV)；c——Calcium(6.42 MeV)；d——Iron(7.64 MeV)Fig.3 Relation between characteristic gamma ray intensity and thickness

3.3.2不同厚度水泥生料

為進一步分析PGNAA方法測量不同厚度物料的特性，分別利用蒙特卡羅模擬和實驗測試，研究Al、Si、Ca、Fe元素的特征計數隨水泥生料樣品厚度變化的規律。由于Al(7.73 MeV)和Fe(7.64 MeV)的特征射線能量值接近，為準確分析，采用能量分辨率較高的高純鍺探測器。水泥生料樣品密度為1.6 g/cm3，所含Al2O3、SiO2、CaO、Fe2O3分別為3.2%、12.3%、42.6%、1.9%。模擬與實驗結果示于圖4。由圖4結果可知，水泥生料中Al2O3、SiO2、CaO、Fe2O3的特征射線計數均隨物料厚度增長呈現非線性增長規律，厚度小于10 cm時幾乎呈線性增加，隨后計數增加率變小，在20 cm處伽瑪計數趨于飽和。

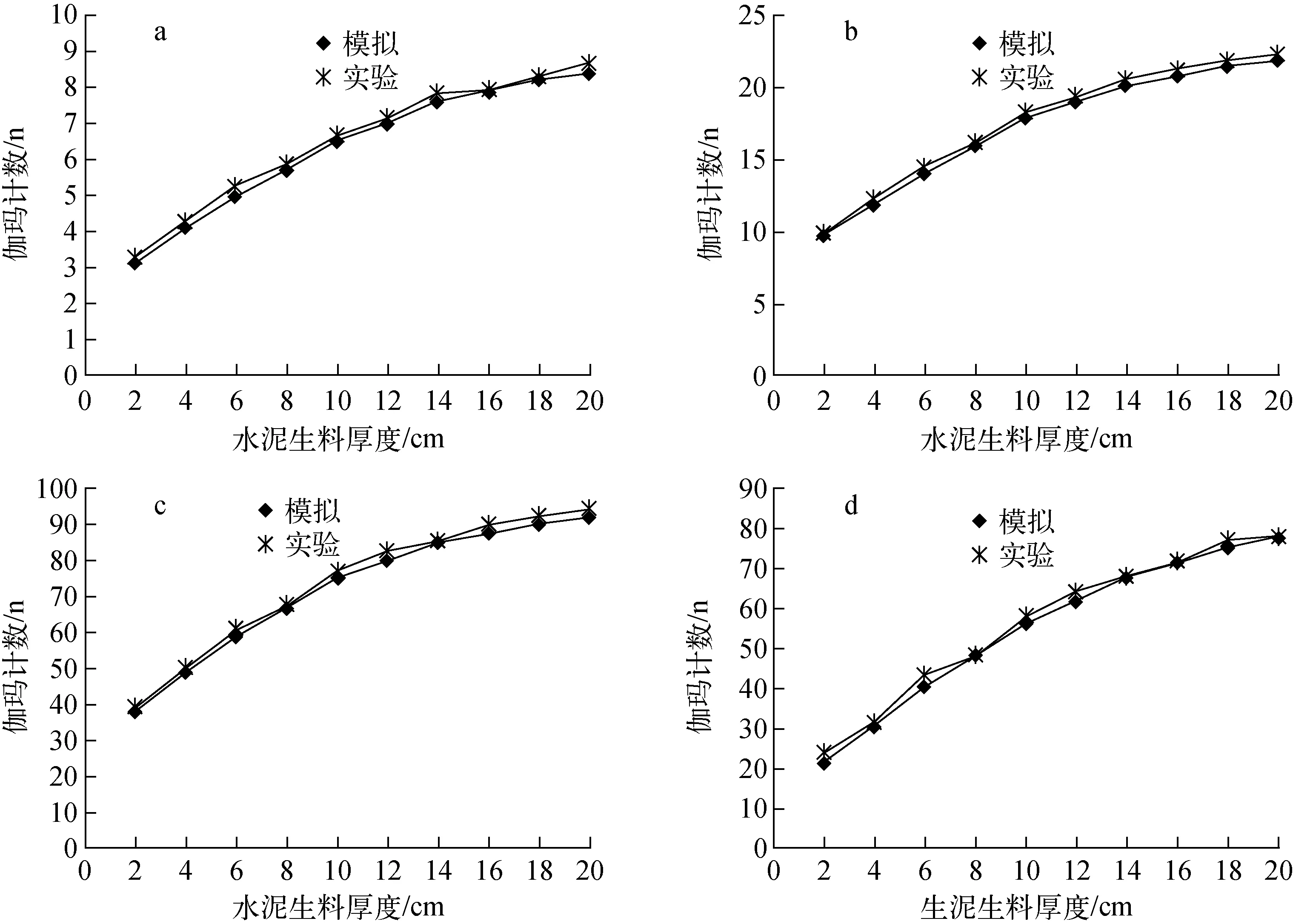
a——鋁(7.73 MeV)；b——硅(4.93 Mev)；c——鈣(6.42 Mev)；d——鐵(7.64 MeV)圖4 元素特征伽瑪射線強度與水泥生料厚度關系a——Aluminum(7.73 MeV)；b——Silicon(4.93 Mev)；c——Calcium(6.42 Mev)；d——Iron(7.64 MeV)Fig.4 Relation between characteristic gamma ray intensity and cement raw thickness

4 修正模型

4.1 單質樣品

4.1.1Al，Si，Ca

由于PGNAA測量過程中物料內部的中子自屏蔽和伽瑪自衰減效應的影響，元素的特征瞬發伽瑪射線計數隨物料厚度增長呈非線性增長。為此，尋求修正模型，使修正后的射線計數率與物料的厚度變化呈線性增長。首先分析密度較小、質量變化范圍較小的Al2O3、SiO2、CaO的修正模型，采用二次多項式進行修正，結果示于圖5。

由圖5中Al2O3、SiO2、CaO的特征伽瑪射線與相對質量(厚度乘以密度)的關系，得到元素Al、Si、Ca的含量修正模型：

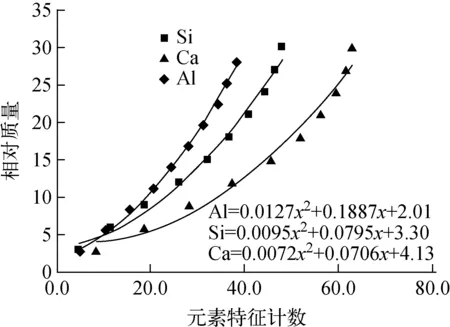
圖5 元素修正模型Fig.5 The correction model of elements

Y=a*X2+b*X+c

(4)

Al=Al*Y

(5)

Si=Si*Y

(6)

Ca=Ca*Y

(7)

式中，X為特征伽瑪計數，Y為修正參數。公式(4)為修正參數計算公式，公式(5)、(6)、(7)分別是Al、Si、Ca的含量修正公式。

4.1.2Fe

Fe粉的含量修正模型示于圖6。由于Fe粉密度較大，與Al2O3、SiO2、CaO相比，相同厚度的Fe粉質量較大，物料內部的自屏蔽與自衰減效應較強，導致在物料厚度為8 cm，相對質量為30時，計數率出現拐點，Fe含量無法用通用的修正模型改善測量。因此，當物料厚度和質量變化較小時，可采用多項式修正模型減小自屏蔽與自衰減效應帶來的非線性影響；當物料厚度和質量過大時，射線計數出現飽和與下降趨勢，無法找到較好的修正模型改善測量精度，只有改善測量條件，如減小被測量物料的厚度或保持物料厚度恒定不變實現測量。

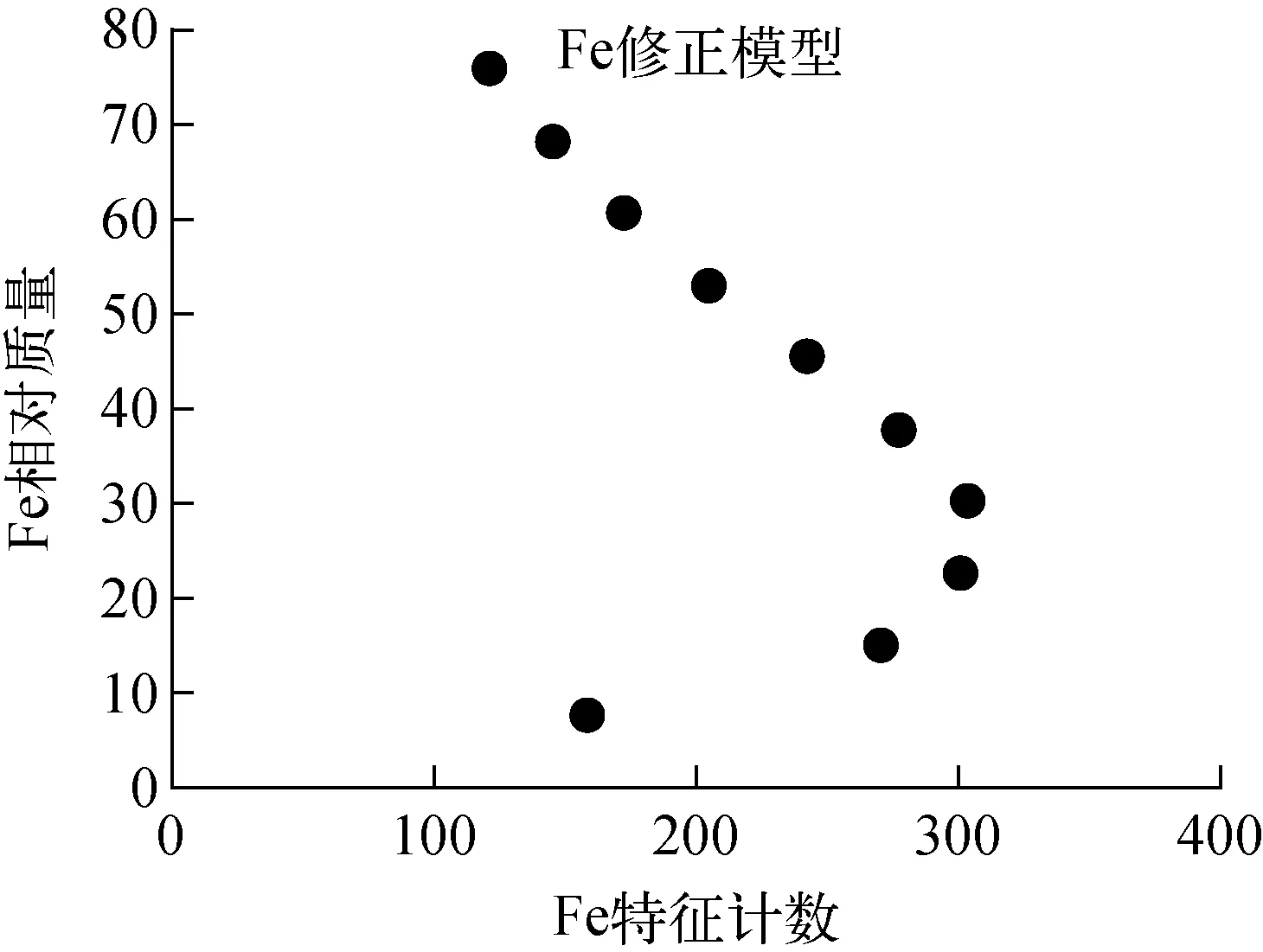
圖6 Fe元素修正模型Fig.6 Fe element correction model

4.2 水泥生料

根據對單質樣品的計數修正模型的分析與PGNAA測量水泥生料的伽瑪計數隨厚度變化的非線性規律，考慮采用二次多項式修正模型。水泥生料中Al2O3、SiO2、CaO、Fe2O3的特征計數與相對質量的變化關系及修正模型示于圖7。

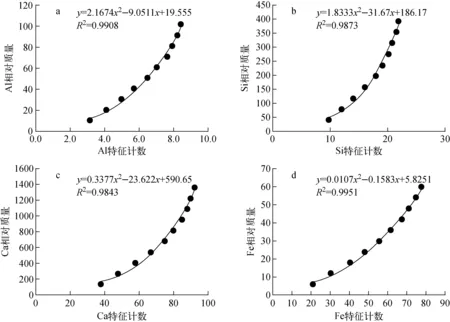
a——Al；b——Si；c——Ca；d——Fe圖7 水泥生料元素修正模型a——Al；b——Si；c——Ca；d——FeFig.7 Element correction model for cement raw

如果不考慮各元素的特征射線計數隨水泥生料厚度變化的非線性規律，即認為特征伽瑪計數隨厚度變化完全線性增加，則考慮采用特征伽瑪計數與元素相對質量的一元線性擬合，即線性標定。線性標定得到的各元素相對誤差示于圖8。由圖8結果可以看出，不同厚度各元素的相對測量誤差較大，多數情況下相對誤差超過10%。

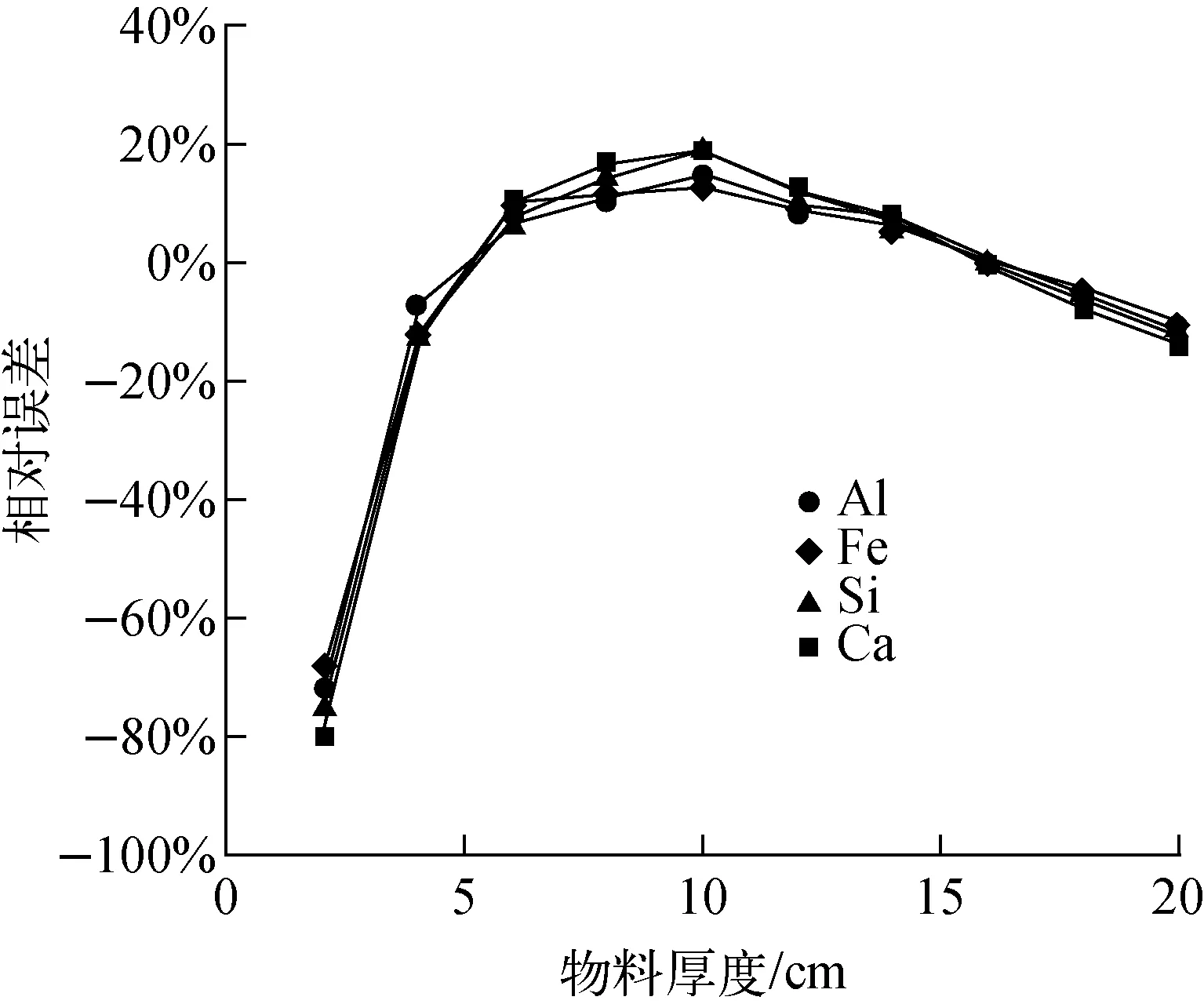
圖8 線性標定的測量相對誤差Fig.8 Measurement relative error of linear calibration

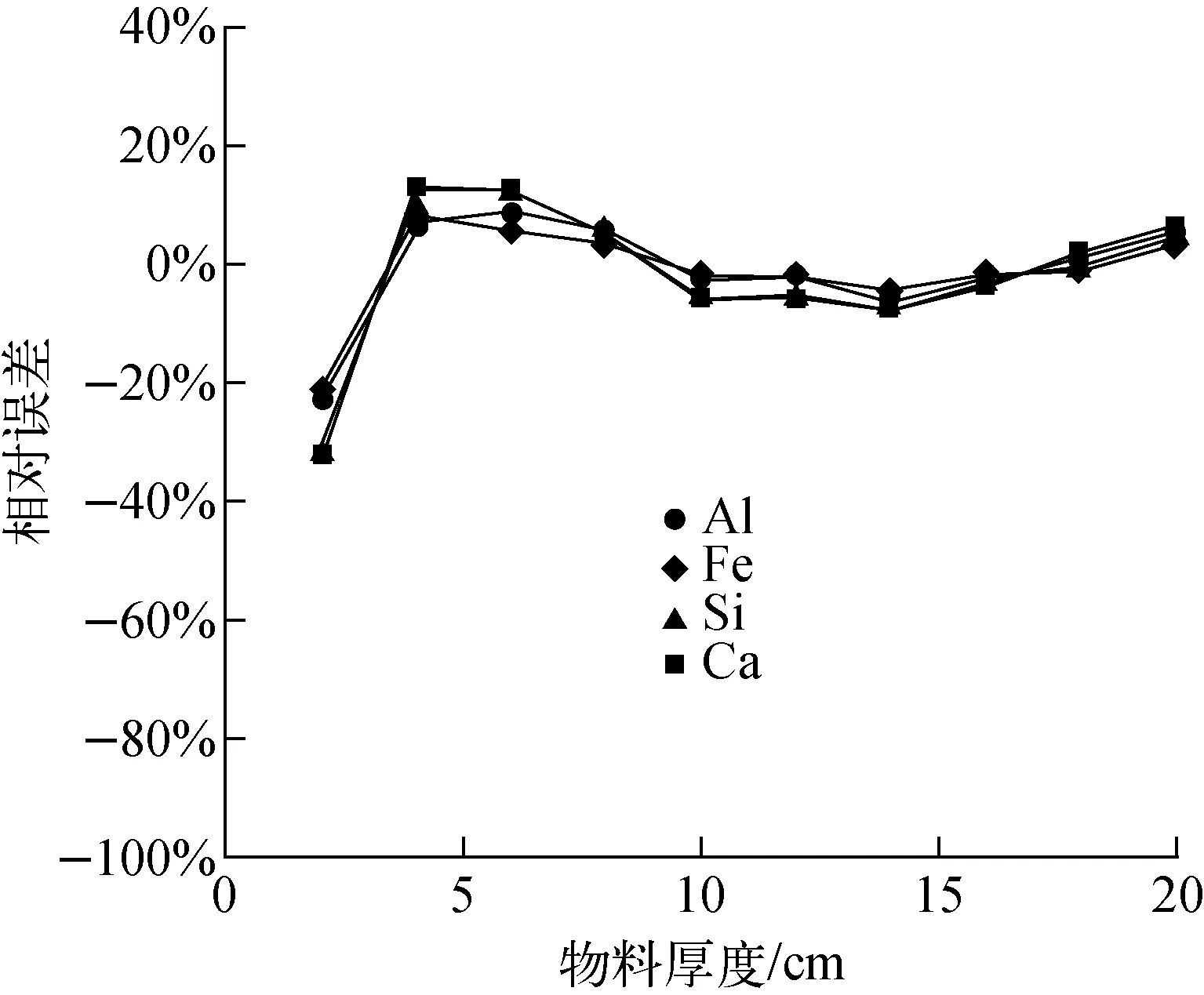
圖9 厚度修正后的測量相對誤差Fig.9 Measurement relative error after thickness correction

經過多項式厚度模型修正后，水泥生料Al2O3、SiO2、CaO、Fe2O3的測量值與實驗值相對誤差示于圖9。與線性標定的相對測量誤差相比，經厚度修正后，各元素的相對誤差明顯減小，只有個別情況下相對誤差超過10%。Al2O3、SiO2、CaO、Fe2O3相對誤差的標準偏差分別降低36%、46%、46%、33%。

從修正模型的擬合相關系數看，Al2O3、SiO2、CaO、Fe2O3的擬合相關性較高，達到0.98以上，說明水泥生料的厚度修正模型具有較好的適用性。但修正后各元素的相對誤差仍較大，尤其厚度為2 cm時各元素的相對誤差達到20%，說明物料厚度過薄(小于2 cm)時，二次多項式厚度修正模型的修正效果較差。當物料厚度較薄時，可以采用分段函數進行修正。但考慮水泥工業現場，皮帶上物料的厚度通常集中在10～20 cm，可以忽略物料厚度過小情況下厚度修正模型偏差較大的問題。

5 結論

通過蒙特卡羅模擬與實驗測量，利用PGNAA方法測量不同厚度物料時得到以下結論。

(1) 當物料厚度較小時，元素的特征瞬發伽瑪射線強度近似隨物料厚度的增加而線性增加；當物料厚度較大時，元素的特征瞬發伽瑪射線強度隨物料厚度的增長率變慢，當物料增加到過厚時，甚至出現下降情況。

(2) 當物料厚度變化范圍較小，可以通過多項式修正模型減小自屏蔽與自衰減效應帶來的非線性影響。通過多項式厚度修正模型修正后，與線性標定相比，測量相對誤差降低30%以上；當物料厚度過大，計數率達到飽和并下降后，修正模型不再適用。需要減小物料厚度或約束物料厚度為恒定值。

通過PGNAA方法測量不同厚度水泥生料的研究，采用修正模型在一定程度上消除了物料厚度變化對測量結果的非線性影響，此修正方法可以推廣到透射式跨皮帶PGNAA在線分析儀測量煤質、燒結料、鋁土礦等塊狀物料的檢測。