創新命題 推陳出新
——電場與磁場創新題賞析(一)

■江蘇省江陰高級中學 徐漢屏(特級教師)

電場與磁場相關知識是高中電磁學的基礎,是歷年高考的熱點之一,主要涉及電場強度、電勢、電勢能、磁感應強度等概念的分析,帶電粒子在電場或磁場中運動的計算等。在2018年各地模擬試卷和高考卷中出現了不少關于電場和磁場的創新題,值得關注。

一、電場創新題賞析

創新題1:如圖1所示,空間有一圓錐O B B′,點A、A′分別是兩母線的中點。現在頂點O處固定一正的點電荷,下列說法中正確的是( )。

A.A、A′兩點的電場強度相同

B.平行于底面的圓心為O1的截面為等勢面

C.將一正的試探電荷從A點沿直徑移到A′點,靜電力對該試探電荷先做正功后做負功

D.若B點的電勢為φB,A點的電勢為φA,則B A連線中點C處的電勢φC小于

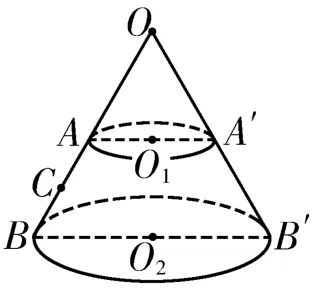
圖1

解析:由點電荷的電場線分布情況可知,A、A′兩點的電場強度大小相等,方向不同。由等勢面與電場線垂直可知,平行于底面的圓心為O1的截面不是等勢面。將一正的試探電荷從A點沿直徑移到A′點,該試探電荷相對O處固定的正點電荷先靠近后遠離,靜電力對該試探電荷先做負功后做正功。將點電荷產生的電場的微小區域視為勻強電場,則由U=E d并累加可知,UAC＞UCB,即φA-φC＞φC-φB,解得答案為D。

A.電荷Q是正電荷

B.A、B、C三點電勢的大小關系是φA=φC＞φB

C.A、B、C三點場強的大小關系是EA=EC＞EB

D.該粒子經過A、B、C三點時動能的大小關系是EkA=EkC＞EkB

圖2

提示:帶電粒子運動的軌跡向外側彎曲,說明粒子所受靜電力向外,因為粒子帶負電,所以電荷Q是負電荷。在負點電荷產生的電場中,電場線方向由無限遠處指向負點電荷,順著電場線方向電勢降低,因此φA=φC＞φB。在點電荷產生的電場中,離場源電荷越近,場強越大,所以EA=EC＜EB。帶電粒子在運動過程中遵循能量的轉化和守恒定律,即EkA+EpA=EkB+EpB=EkC+EpC,因為φA=φC＞φB,根據Ep=q φ,考慮到q是一個負電荷,所以EpA=EpC＜EpB,由此可得EkA=EkC＞EkB。答案為B D。

小結:創新題1與上述常規題均涉及電場強度與電勢的分析,而創新題1在上述常規題的基礎上,將平面內的分析拓展到了立體空間,對分析能力提出了更高的要求。

現學現練:如圖3所示,勻強電場中的點A、B、C、D、E、F、G、H 為立

方體的八個頂點。已知G、F、B、D四點的電勢分別為5V、1V、2V、4V,則A 點的電勢為( )。

A.0

B.1V

C.2V

D.3V

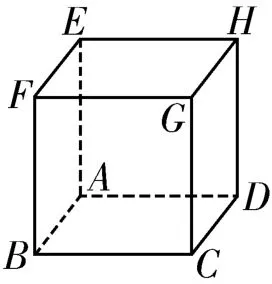
圖3

思路點撥:本題與創新題1均要求在空間范圍內對電場進行分析。在勻強電場中,由公式U=E d可知,沿著任意方向前進相同距離,電勢差必定相等。因為G F∥C B,且G F=C B,所以φG-φF=φC-φB,即φC=φG-φF+φB=5V-1V+2V=6V。同理,φA-φB=φD-φC,φA=φB+φD-φC=2V+4V-6V=0。答案為A。

創新題2:空間存在一靜電場,電場中的電勢φ隨x的變化規律如圖4所示。下列說法中正確的是( )。

A.x=4 m處電場強度可能為零

B.x=4m處電場方向一定沿x軸正方向

C.電荷量為e的負電荷沿x軸從O點移動到x=6m處,電勢能增大8e V

D.沿x軸正方向,場強先增大后減小

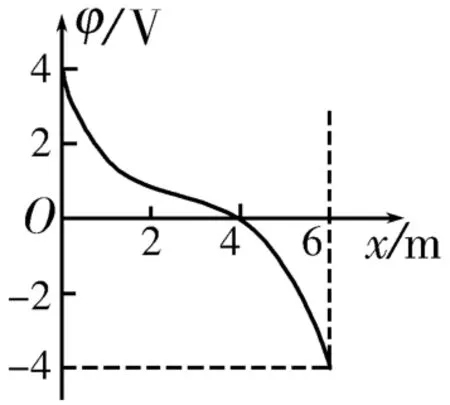
圖4

解析:φ-x圖像的斜率的絕對值等于電場強度沿x軸方向分量的大小,因此x=4m處電場強度不為零。從x=0到x=6m處電勢不斷降低,但x=4m處電場方向不一定沿x軸正方向。電荷量為e的負電荷沿x軸從O點移動到x=6m處,電勢能增大量ΔEp=e U=8e V。沿x軸正方向,φ-x圖像斜率的相對值先減小后增大,因此電場強度先減小后增大。答案為C。

A.EBx的大小大于ECx的大小

B.EBx的方向沿x軸正方向

C.電荷在O點受到的靜電力在x軸方向上的分量最大

D.負電荷沿x軸從B點移動到C點的過程中,靜電力先做正功,后做負功

圖5

提示:φ-x圖像的斜率的絕對值等于電場強度沿x軸方向分量的大小,因此EBx＞ECx。同理可知,O點場強在x軸方向上的分量最小,電荷在該點受到的靜電力在x軸方向上的分量最小。沿電場線方向電勢降低,在O點左側,EBx的方向沿x軸負方向,在O點右側,ECx的方向沿x軸正方向。負電荷所受靜電力的方向與場強相反,由此負電荷沿x軸從B點移動到C點的過程中,靜電力先做正功,后做負功。答案為A D。

小結:創新題2與上述常規題同屬對電場中φ-x圖像的分析,不同的是創新題2的圖像延伸到了x軸下方,且既需定性分析,又需定量計算,難度有所增加。

現學現練:a、c、d、b依次為x軸上的四個點,a與b、c與d均關于原點O對稱。a、b兩點固定著兩個電荷量相等的點電荷,如圖6所示的Ex-x圖像描繪了x軸上部分區域的電場強

度變化情況(以x軸正方向為電場強度的正方向)。下列判斷正確的是( )。

圖6

A.c、d兩點的場強相同

B.c、d兩點的電勢相同

C.正的試探電荷從c點移動到d點靜電力做負功

D.負的試探電荷在c處的電勢能較d處的大

思路點撥:本題與創新題2均是電場的圖像分析問題,只是由φ-x圖像變成了Ex-x圖像。a、b兩點固定著兩個電荷量相等的點電荷,中點O處的電場強度為負值,說明兩點電荷是等量異種電荷,且a、b兩點分別為負電荷和正電荷。根據兩等量異種點電荷電場線的分布情況可知,c、d兩點的場強相同,c點的電勢低于d點的電勢,負的試探電荷在c處的電勢能較d處的大。正的試探電荷從c點移動到d點,是逆著電場線移動,靜電力做負功。答案為A C D。

二、磁場創新題賞析

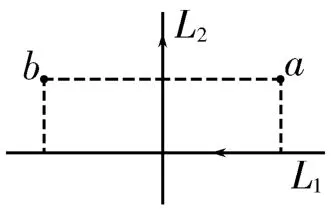
圖7

創新題3:(2018年高考全國Ⅱ卷)如圖7所示,紙面內有兩條互相垂直的長直絕緣導線L1、L2,L1中的電流方向向左,L2中的電流方向向上;L1的正上方有a、b兩點,它們相對于L2對稱。整個系統處于勻強外磁場中,外磁場的磁感應強度大小為B0,方向垂直于紙面向外。已知a、b兩點的磁感應強度大小分別為方向也垂直于紙面向外。則( )。

A.流經L1的電流在b點產生的磁感應強度大小為

B.流經L1的電流在a點產生的磁感應強度大小為

C.流經L2的電流在b點產生的磁感應強度大小為

D.流經L2的電流在a點產生的磁感應強度大小為

解析:設流經L1的電流在a點產生的磁感應強度大小為B1a,方向垂直于紙面向里;流經L2的電流在a點產生的磁感應強度大小為B2a,方向垂直于紙面向里;流經L1的電流在b點產生的磁感應強度大小為B1b,方向垂直于紙面向里;流經L2的電流在b點產生的磁感應強度大小為B2b,方向垂直于紙面向外。因為導線L1、L2相互垂直,且a、b兩點相對于L2對稱,所以B1a=B1b,B2a=B2b。以垂直于紙面向里的方向為正方向,由磁場的矢量疊加法則得答案為A C。

A.1區

B.2區

C.3區

D.4區

圖8

提示:先應用安培定則分析六根通電導線在各區域產生的磁場的方向,再根據磁場的矢量疊加法則可定性判斷出指向紙面內的磁場最強的區域是4區。答案為D。

小結:創新題3與上述常規題均需應用安培定則和磁場的矢量疊加法則,分析幾根通電導線周圍的磁場。創新題3的新穎之處在于需對磁感應強度進行定量計算,其難度明顯大于上述常規題。

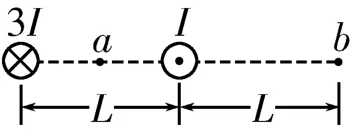
圖9

現學現練:無限長通電直導線在周圍某一點產生的磁場的磁感應強度B的大小與電流成正比,與導線到這一點的距離成反比,即(式中k為常數)。如圖9所示,兩根相距為L的無限長直導線分別通有電流I和3I,在兩根導線的連線上有a、b兩點,a點為兩根導線連線的中點,b點到通有電流I的導線的距離為L。下列說法中正確的是( )。

A.a點和b點的磁感應強度方向相同

B.a點和b點的磁感應強度方向相反

C.a點和b點的磁感應強度大小之比為8∶1

D.a點和b點的磁感應強度大小之比為16∶1

思路點撥:本題與創新題3一樣,需要對通電導線疊加場的磁感應強度進行定量計算,還涉及對題給公式的運用。取豎直向下為正方向,根據安培定則和磁場的矢量疊加法則得a、b兩點的磁感應強度分別為二者的方向相同,大小之比為16∶1。答案為A D。

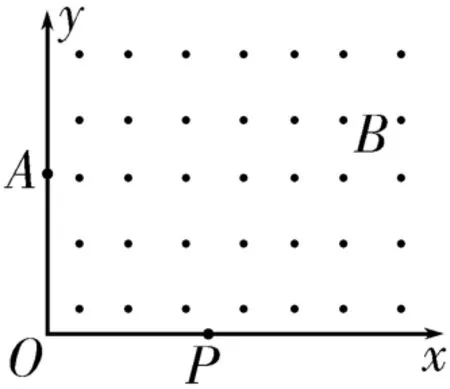
圖10

創新題4:如圖10所示,在平面直角坐標系x O y的第一象限內,存在磁感應強度大小為B的勻強磁場,方向垂直于紙面向外。在y軸上的A點放置一放射源,可以不斷地沿x O y平面內的不同方向以大小不等的速度放射出質量為m、電荷量為+q的同種粒子,這些粒子打到x軸上的P點。已知O A=O P=l,則( )。

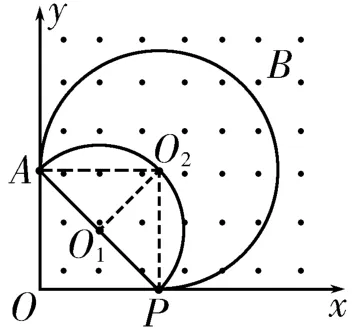
圖11

解析:設粒子的速度大小為v時,其在磁場中的運動半徑為R,由牛頓運動定律得若粒子以最小的速度到達P點,則其軌跡一定是以A P為直徑的圓弧(如圖11中圓O1所示),由幾何關系知sAP=l,R=則粒子的最小速度粒子在磁場中的運動周期設粒子在磁場中運動時的軌跡所對應的圓心角為θ,則粒子在磁場中的運動時間在磁場中運動時間最長的粒子的運動軌跡是圖11中圓O2的一部分,此時粒子的初速度方向豎直向上,由幾何關系得θ=3π,因此粒子在磁場中運動的最

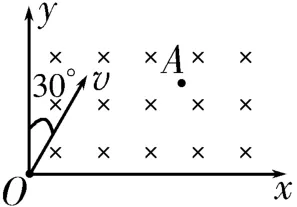
圖12

A.粒子帶正電

B.粒子帶負電

C.粒子由O點到A點經歷的時間t=πm 3q B

D.粒子的速度沒有變化

提示:根據粒子的偏轉方向,由左手定則可知粒子帶負電。粒子由O點運動到A點,速度方向偏轉了60°,故經歷的時間在此過程中,粒子的速度大小未變,但方向發生了變化。答案為B C。

小結:創新題4與上述常規題類似,均涉及帶電粒子在分布于平面直角坐標系第一象限內的勻強磁場中做部分勻速圓周運動,其創新之處在于將粒子沿單一方向的入射,改成了從不同方向以大小不等的速度入射,求解時要求對臨界情況有較強的分析能力。

圖13

現學現練:如圖13所示,空間存在垂直于紙面的勻強磁場,一粒子發射源P位于足夠大的絕緣板A B上方,間距為d,在紙面內向各個方向發射速率均為v的同種帶電粒子,不考慮粒子間的相互作用和粒子自身的重力。已知粒子做圓周運動的半徑也為d,則粒子( )。

B.能打在板上的區域長度是2d

思路點撥:本題與創新題4相似,同樣涉及帶電粒子在勻強磁場中做部分勻速圓周運動的臨界問題。打在板上粒子運動軌跡的臨界狀態如圖14甲所示,根據幾何關系可知,帶電粒子能打在板上離P點的最遠距離s=2R=2d,能打在板上的區域長度l=R+最長和最短的運動軌跡示意圖如圖14乙所R=(1+)d。粒子在磁場中運動時間示,根據幾何關系可知,最長時間最短時間又有粒子在磁場中運動的周期解得答案為C。

圖14

編者注:帶電粒子在電場或磁場中的運動是同學們學習電場和磁場時的重點也是難點,本文僅僅展示了帶電粒子在單一電場或磁場中的運動,下期將著重介紹帶電粒子在電、磁復合場中的運動,敬請期待。